颗粒物质流变学行为和材料参数对颗粒阻尼器能量耗散的影响

苏 凡， 张 航， 尹忠俊

(北京科技大学 机械工程学院， 北京 100083)

颗粒阻尼技术，作为一种有效的振动控制手段，被广泛地应用于航空航天、机械以及土木等领域[1]。颗粒阻尼的原理是在振动结构体上加工一定数量的孔洞，在其中填充适当数量的金属、非金属颗粒或通过将装填有颗粒的空腔附着在结构振动较大的区域，利用颗粒与颗粒以及颗粒与空腔之间的非弹性碰撞和摩擦消耗系统的能量，从而达到减振的目的[2]。

由于颗粒阻尼复杂的非线性阻尼耗能机理，试验和仿真成为研究颗粒阻尼的主要手段。Michon等[3]通过实验探究软中空颗粒在蜂窝结构中的减振效果，并提出简化的理论计算模型；Yang等[4]利用功率测量的方法对颗粒阻尼器的耗能特性进行了试验研究，研究了各因素对阻尼器损耗功率和动态质量的影响；夏兆旺等[5]以填充颗粒的悬臂梁为研究对象，研究了结构阻尼随颗粒各参数呈非线性变化的特性以及颗粒材料、填充率和金属盒的位置对系统阻尼的影响；而周宏伟[6]和段勇等[7]在直升机旋翼上使用颗粒阻尼器，试验表明颗粒阻尼在旋翼非旋转及低转速下可以明显提升系统阻尼，降低旋翼响应水平；Wong等[8]利用PFC3D软件仿真了颗粒阻尼器损耗功率与振动幅值和振动频率间的关系，并利用试验进行了验证；Xiao等[9]基于FEM-DEM的耦合仿真，对安装颗粒阻尼器的旋转齿轮进行了仿真研究，得出了不同尺寸的颗粒的减振效果，并通过实验进行验证。

目前，对颗粒阻尼的研究主要集中在对结构的各阶模态阻尼的贡献和减振效果上，对耗散理论及阻尼器内颗粒系统本身的状态的研究还不够深入。颗粒物质的特殊性就在于它既可以表现出类似于固态、液态、气态的特性，又具有丰富而独特的行为。在一定条件下，它会像液体和气体一样流动，表现出一系列流变学行为。但仅有少量学者对颗粒系统不同运动状态的能量耗散特性进行了研究[10]。并且，对于颗粒物质材料参数对颗粒阻尼器阻尼特性的影响还未被系统的探究。这些在一定程度上阻碍了颗粒阻尼的发展和应用。

近年来，随着对离散单元法的不断改进和计算机技术的发展，离散单元法逐渐成为研究颗粒系统的一种重要手段。离散单元法能够准确得到NOPD中单个颗粒的受力与运动，为分析NOPD中颗粒系统的能量耗散规律提供足够的信息[11]。

鉴于此，本文采用离散元法对颗粒阻尼器进行了仿真研究，结合阻尼器中颗粒系统的运动状态探究不同振动参数下颗粒阻尼器的阻尼效果，从细观尺度上阐释颗粒系统的能量耗散特性。并且针对影响颗粒阻尼减振特性的内在因素，通过正交试验，考察了颗粒的材料参数对损耗因子的影响，为颗粒阻尼器的优化设计和应用提供理论依据。

1 仿真模型及参数

1.1 离散单元法

本文使用的颗粒模型是软球模型，颗粒的法向力被简化成一个弹簧阻尼元件，切向力被简化成一个弹簧阻尼元件和一个滑动摩擦元件，并引入弹性系数和阻尼系数等参数来量化弹簧、阻尼器、滑动器的作用，不考虑颗粒表面变形，依据颗粒间法向重叠量和切向位移计算接触力。所采用的接触模型是无黏球形颗粒的 Hertz-Mindlin 模型[12]，该模型采用 Hertz 理论计算法向力，采用 Mindlin 方法[13]来计算切向力。设半径为R1、R2的两球形颗粒发生弹性接触，则法向重叠量δn为：

δn=R1+R2-|c1-c2|>0

(1)

式中:R1和R2是两球的半径;c1和c2是两球球心的位置矢量。

颗粒间的接触面为圆形，则接触面的半径a为：

(2)

法向力表示为

(3)

式中:nc为颗粒i球心到颗粒j球心的单位矢量，n=Ri/|Ri|；v为颗粒i球心到颗粒j间的相对运动速度矢量，vnij=vi-vj；kn为法向刚度，根据Hertz接触理论确定：

(4)

式中:E*和R*分别为有效弹性模量和有效颗粒半径，可由下式求得：

(5)

(6)

式中:E1、μ1和E2、μ2分别为颗粒1和颗粒2的弹性模量和泊松比。

颗粒间的切向力可表示为：

Fct=-ktδt+dt(vtij·nc)nc

(7)

式中:δt为切向重叠量，即接触点的切向位移；vtij为接触点的滑移速度：

vtij=vj-vi+ωj×Rj-ωi×Ri

(8)

kt为切向刚度，由 Mindlin等[13]接触理论确定，其表达式为：

(9)

G*是有效剪切模量，其值可由下式给定：

(10)

式中:G1、G2是两颗粒的剪切模量，其值是由弹性模量和泊松比确定的：

(11)

(12)

而对于接触当中的能量耗散现象，除了库伦摩擦外，则使用Tsuji等[14]提出的以下非线性黏性阻尼来计算阻尼系数：

(13)

式中:m*为颗粒等效质量；ζ为等效黏性阻尼比，分别由以下两式求出：

(14)

(15)

式中:mi、mj分别为两颗粒的质量；e为恢复系数。

1.2 仿真模型

本文建立的3D NOPD 颗粒系统仿真模型如图1所示，颗粒系统由一个密闭的有机玻璃圆柱容器(D×H=26 mm×78 mm)和装填在其中的500颗钢球(d=3.5 mm)组成。仿真采用的模型及材料基于文献[10]中已验证的模型，相关参数设置如表1所示。容器受到竖直方向的正弦激励，仿真的两个主要控制参数为激振频率f(15～90 Hz)和激振加速度Γ(1～30 g)。

图1 DEM颗粒阻尼仿真模型 Fig.1 DEM model of the NOPD

仿真参数数值颗粒材料密度ρ/(kg·m-3)7800颗粒材料弹性模量Ep/Pa206E+009颗粒材料泊松比μp0.3颗粒直径d/m0.0035总颗粒数量500容器材料密度ρc/(kg·m-3)1190容器材料弹性模量Ec/Pa3.3E+009容器材料泊松比μc0.37恢复系数e0.92静摩擦因数μs0.3滚动摩阻系数μr0.01时间步Δt/s2.07E-007仿真时间t/s2

2 结果与讨论

2.1 颗粒系统运动状态及相图

颗粒系统在垂直振动的条件下，会呈现出如类固态[10]、流化、蹦床[15]、对流[16]、莱顿弗罗斯特效应[17]等基于振动颗粒物质流变特性的运动状态。通过仿真，本文把NOPD中颗粒系统的运动形态分为类固态、局部流化、全局流化、蹦床、对流、莱顿弗罗斯特效应及浮力对流七种。图2为在不同激振条件下，七种颗粒系统运动形态图及对应速度矢量图，从中可以获得每种运动形态的特性。

当振动加速度低于1.2 g时，颗粒系统表现为类固态，此时容器中的颗粒之间、颗粒与容器壁之间几乎没有相对运动，整个阻尼器相当于一个附加质量块。

当振动加速度达到1.2 g，颗粒物质在“固”、“液”两种状态之间的转变出现。颗粒系统中底部颗粒仍旧没有发生相对运动，但表面颗粒开始流化，系统进入局部流化状态，开始表现出类似液态的行为特性。图2(b)可以看到顶部颗粒层中颗粒的轻微相对运动。

随着激振频率和振幅的增加，当局部流化的范围不断扩大至整个颗粒系统时，容器中的所有颗粒层的颗粒都发生相对运动，整个颗粒系统处于一个整体流化的状态，即图2(c)中的全局流动状态。

蹦床状态出现在振幅较大的区域。在蹦床系统中，颗粒就像无弹性的跳跃的小球，在容器中进行杂乱无章的碰撞运动。

对流发生时，不仅颗粒之间存在相对运动，不同颗粒层中的颗粒还会进行颗粒位置的交换，整个颗粒系统就像受热不均的液体。图 2(e)对应于频率为65 Hz时颗粒系统速度矢量图，可以看到颗粒层中浮动着流动的对流卷。

颗粒的莱顿弗罗斯特效应发生在大振动强度大振幅条件下，颗粒分布出现明显的Z向密度逆反，即一簇具有六角密排结构的密集颗粒簇被下方一些剧烈运动着的稀少颗粒托起，持续的激励使下方稀疏的颗粒层不断发生振荡，同时上方稠密的颗粒层稳定的浮动在几乎相同的位置。底部运动剧烈的颗粒相当于蒸汽层，上部颗粒相当于悬浮层[17]。

浮力对流可以看作颗粒莱顿弗罗斯特效应与对流两种状态的叠加，当莱顿弗罗斯特现象中悬浮的颗粒层中产生对流运动，可以称为浮力对流状态。从图2(g)中的速度矢量图可以看到，悬浮的颗粒层中也浮动着流动的对流卷。

此外，还可以通过颗粒系统的势能曲线看出不同流变行为的特征。本文选取了其中有代表性的四种运动形态随时间变化的势能曲线，如图 3。可以看到，在局部流化状态时，颗粒系统只有表面颗粒流化，因此势能变化很小且稳定在一个较小值；同样波动很小的还有浮力对流状态，莱顿弗罗斯特效应使大部分颗粒稳定悬浮在特定高度，因此势能也稳定在略大于局部流化状态的特定数值；对流状态时颗粒运动明显增加，因此势能变化较大；势能变化最大的是蹦床状态，颗粒在整个容器内剧烈运动，势能波动也相当明显。

图3 颗粒系统的势能曲线 Fig.3 Potential energy curves of granular system in NOPD

为了更清晰直观地表示颗粒系统出现不同运动状态的条件，本文绘制了NOPD在不同振动条件下的颗粒系统运动状态相图。

从图4中可以直观地观察到颗粒系统运动状态的转变，值得注意的是全局流动状态是系统继续过渡至其他状态的基础。相比其他状态，对流是一个较不稳定的状态，它与全局流动的状态界限不像其他状态转化界限那么清晰。莱顿弗罗斯特效应和浮力对流均发生在高振幅高频率下，但相比莱顿弗莱斯特效应，浮力对流状态发生在更大的振动强度条件下，即颗粒系统达到产生莱顿弗莱斯特现象的条件后，继续增大振动强度可使系统转化为浮力对流状态。

2.2 颗粒系统损耗因子

损耗因子是衡量系统的阻尼特性并决定其振动能量耗散能力的重要参数。将一个阻尼器的阻尼容量定义为一个完整周期运动中的能量耗散，即

ΔU=Edissipated=fddx

(16)

该表达式通过位移-力平面上的迟滞环路面积得到。如果系统最初(总)的能量表示为Umaximum，那么比阻尼容量D通过下面的比值得到：

(17)

损耗因子η等于在一个周期内每弧度的比阻尼容量。因此

(18)

式中:Edissipated为一个周期内的能量耗散，Emaximum为周期内初始最大能量，近似等于周期内最大动能。在能量分析中，很多重要参数如阻尼比、阻尼系数都与损耗因子有联系，因此本文引入损耗因子[8, 18]来衡量不同条件下NOPD颗粒系统的阻尼效果。

从图4中选取四个经历过较多状态转变的频率，分别绘制出仿真获得的不同激振频率下的颗粒系统能量耗散、最大动能及损耗因子曲线。图5、6可以看到一个周期内的能量耗散随着振动强度的增加而增加；且频率越大，增加的幅度越小，大频率时能量耗散几乎稳定在一个较小值。周期内最大动能有相似的变化趋势，但在大频率大振动强度条件下， 最大动能的值会略微减小。

图5 不同激振频率下颗粒系统能量耗散图6 不同激振频率下颗粒系统最大动能图7 不同激振频率下颗粒系统损耗因子Fig.5TheenergydissipationinacycleversusexcitationintensityunderdifferentfrequencyFig.6themaximumkineticenergyinacycleversusexcitationintensityunderdifferentfrequencyFig.7Lossfactorversusexcitationintensityunderdifferentfrequency

图7为不同激振频率下颗粒系统损耗因子随振动强度变化曲线，对比不同曲线可以发现，不同激振频率下的颗粒阻尼器表现出最好的阻尼效果时对应的振动强度是不同的。 当系统的激振频率较小(f=30 Hz或50 Hz)时，损耗因子的最大值出现在振动强度较小的条件下；而当系统的激振频率较大(f=70 Hz或90 Hz)时，随着振动强度的变化，损耗因子在经历波动后会呈不断上升的趋势并达到另一个高峰，且损耗因子的最大值出现在振动强度较大的条件下。

结合相图，可以用颗粒系统运动状态的转变来解释损耗因子数值产生的变化。

当振动强度较小时，颗粒系统表现为类固态。此时NOPD相当于附加质量块，损耗因子很小。增大振动强度或增大振幅都会使颗粒系统中尤其是位于颗粒系统上层的颗粒运动加剧，使系统状态由类固态转化为局部流化，此时颗粒之间，颗粒与容器壁之间的碰撞次数增加，系统耗能增加，但系统最大动能仍然很小，因此损耗因子的数值会有大幅度的提升。

低频条件下，振动强度的增大意味着振幅的增大，颗粒系统由流化态转变为蹦床状态。蹦床状态中剧烈的碰撞和较多的碰撞机会耗散了很大的能量，而随着振动条件的变化，频率的增加和振幅的减小都会使碰撞的剧烈程度显著减小，使损耗因子的数值减小。同时，损耗因子的数值不会随着振动强度的增加无限增大，因为此时大部分碰撞是颗粒与容器壁之间的碰撞，这些过于混乱的颗粒运动和碰撞产生倍周期分岔现象，反而不利于系统减振[19]，因此当频率为30 Hz时，损耗因子的数值很小，几乎稳定在0.12附近。

相比其他状态，对流是一个较不稳定的状态，它与全局流动状态的界限不像其他状态转化界限那样清晰，出现的范围也存在一定周期性，随着振动强度的增大，对流在更高的频率下出现。因此两者的损耗因子数值差距也不大，但发生对流运动时，颗粒系统周期变化的方向性给颗粒带来更多的碰撞机会，这意味着对流状态时的损耗因子比全局流动状态略微较大。

莱顿弗罗斯特效应和浮力对流状态这两种状态的发生都是基于颗粒的莱顿弗莱斯特现象，可以说浮力对流是莱顿弗莱斯特现象中的特殊情况，因此都需要满足高振幅高频率的振动条件。发生颗粒的莱顿弗莱斯特现象时，颗粒系统上部悬浮着的密集颗粒层被系统底部稀疏的剧烈运动颗粒托起，相比其他状态，除了颗粒与颗粒之间、颗粒与容器之间碰撞耗散的能量之外，莱顿弗莱斯特现象的发生还需要耗散额外的能量转化为上部悬浮颗粒层的势能。因此，这两种状态下的损耗因子数值相对较大。但相比莱顿弗莱斯特效应，浮力对流状态发生在更大的振动强度条件下。这是因为发生莱顿弗罗斯特效应和浮力对流两种状态时，颗粒系统中悬浮颗粒层的细观组成结构是不同的，莱顿弗莱斯特效应中的悬浮层颗粒相当于类固态为六角密排结构，而浮力对流状态下悬浮层中的颗粒发生的是对流运动，此时颗粒系统需要更多的能量来使悬浮层中的颗粒发生对流运动。类比于类固态和对流状态时损耗因子数值的关系，浮力对流状态时悬浮层中颗粒的碰撞与摩擦耗散的能量多于莱顿弗莱斯特效应。因此，当颗粒系统处于浮力对流状态时，NOPD表现出最好的阻尼效果。

2.3 颗粒材料影响参数正交试验

NOPD中颗粒材料参数是影响阻尼效果的重要内在原因之一，考虑到外界激励对于阻尼性态影响重大，为了探索密度、剪切模量、恢复系数、静摩擦因数、滚动摩擦因数五种颗粒的材料参数对阻尼效果的影响，并综合考虑计算资源本文在颗粒系统处于七种运动状态，分别采用正交试验法进行研究。不仅可以确定各个因素的影响主次，同时对计算资源的需求较低。不同运动状态对应的外界激励水平如表2。

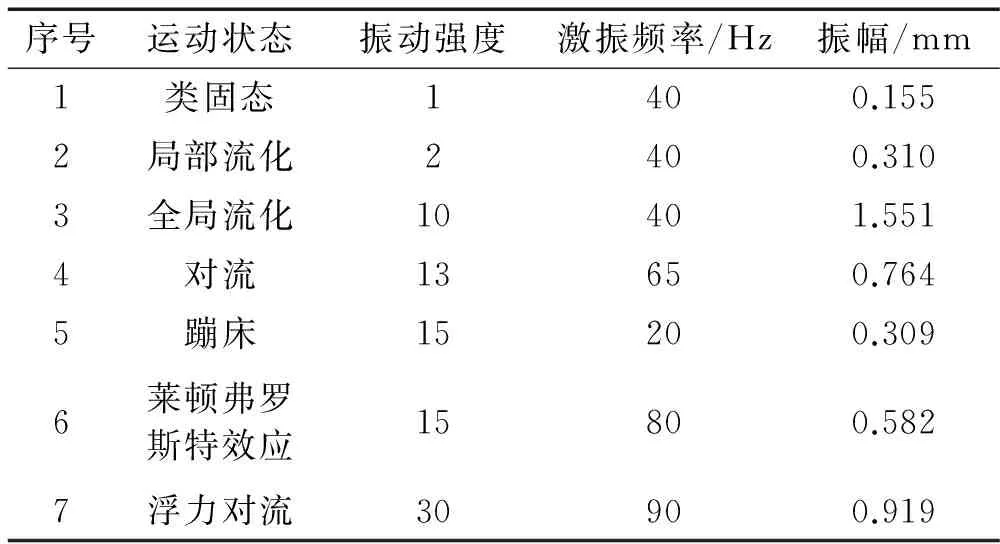
表2 不同运动状态对应的外界激励水平表Tab.2 External excitation levels corresponding todifferent motion modes table

现以全局流化状态下正交试验过程为例，因素和水平的选取如表3所示，选用正交表L16(45)如表4，确定试验方案。

表3 影响NOPD阻尼效果的因素水平表Tab.3 Factors and their levels used in the orthogonal table

正交试验方案如表4所示，分别对16组工况进行仿真，并计算颗粒系统的损耗因子，结果如表5所示。其中极差按照下式计算：

R=max{K1,K2,K3,K4}-min{K1,K2,K3,K4}

式中：Ki为任一列水平号为i所对应试验结果之和，R为极差。

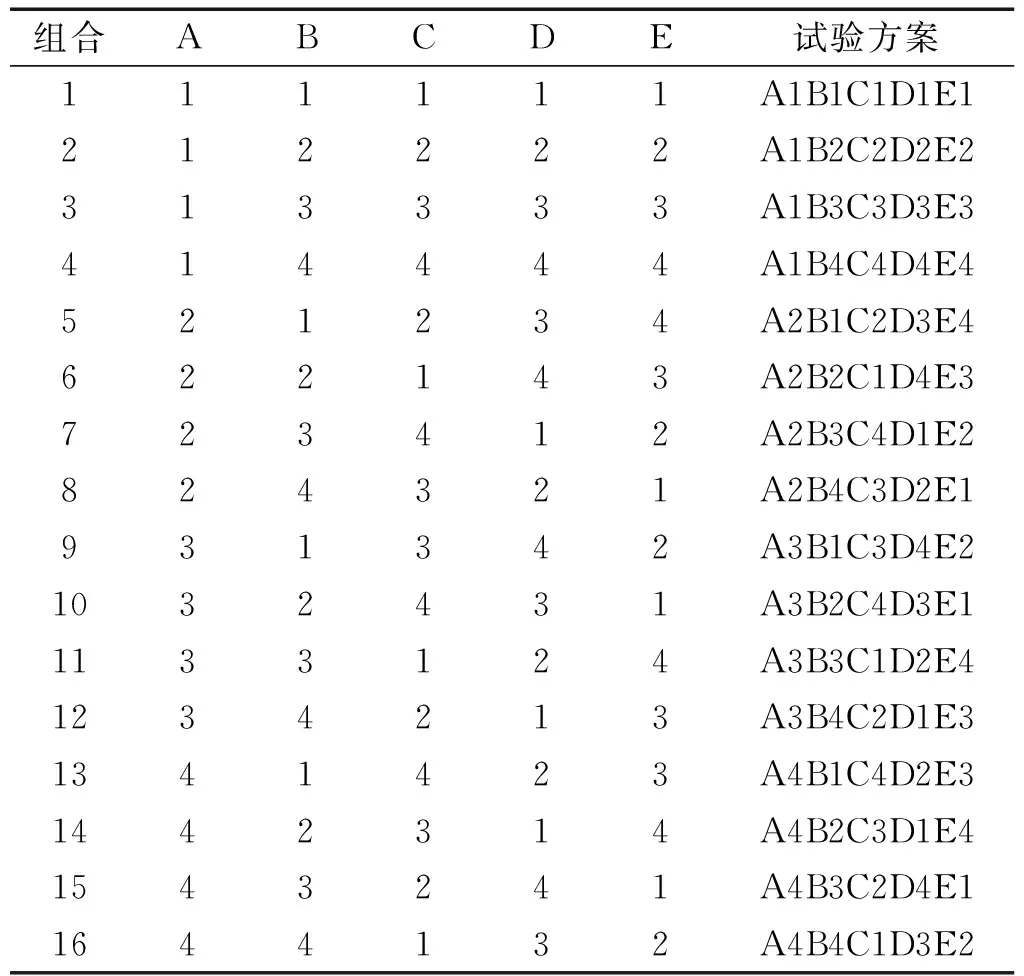
表4 正交表Tab.4 The orthogonal table

由表5分析可知，五个因素在颗粒系统阻尼效果的影响程度上主次是：静摩擦因数>颗粒密度>剪切模量>滚动摩擦因数>恢复系数。

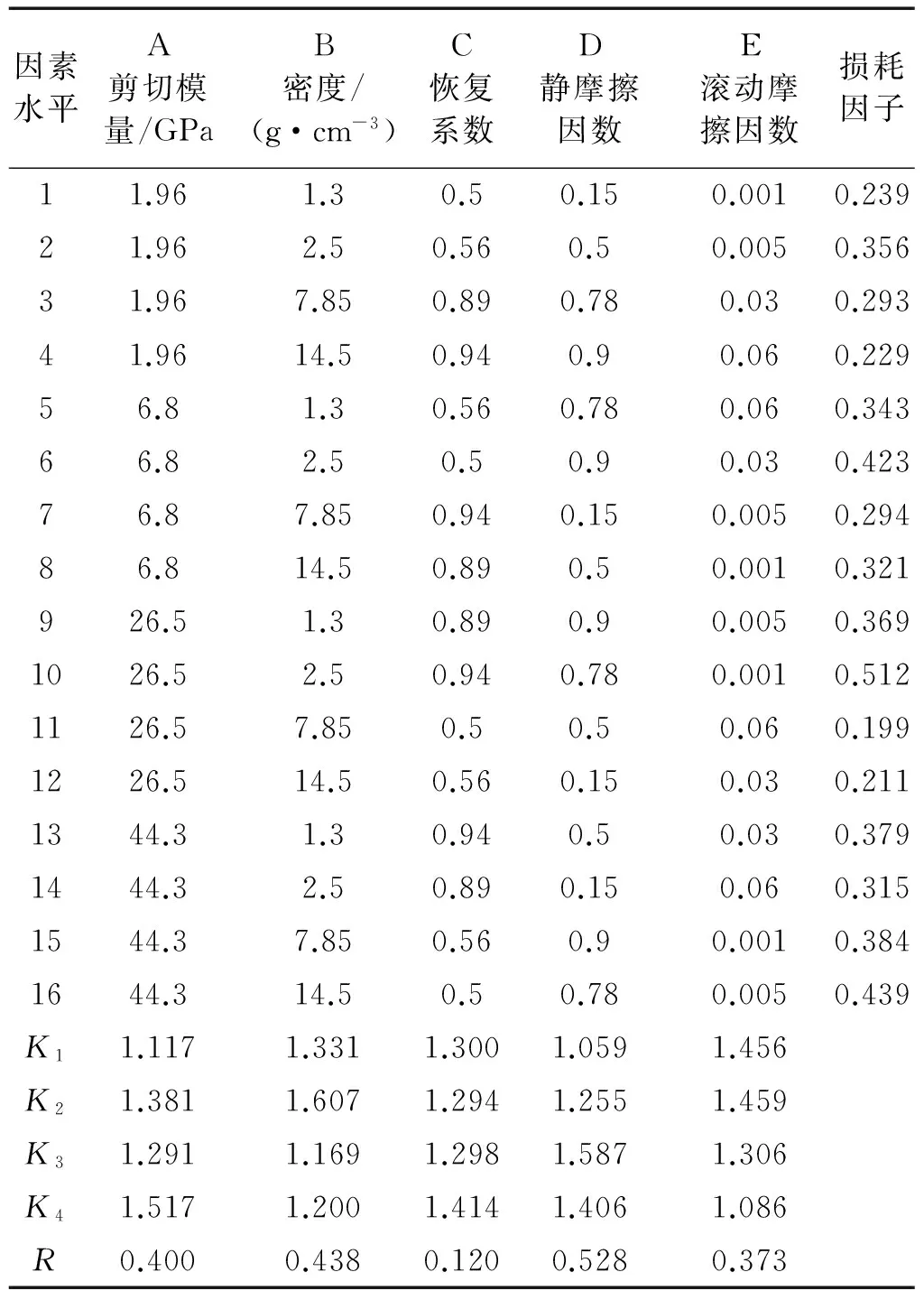
表5 仿真颗粒系统损耗因子结果表Tab.5 The orthogonal test data and analysis results of theloss factor in the simulation

表6为七种状态下分别进行正交试验后得到的极差及影响主次排序。

表6 不同运动状态下正交试验结果表Tab.6 The results of orthogonal test data in differentmotion modes

从表6中可以看到， 当颗粒系统处于类固态时，颗粒进入一种密集块状的状态，颗粒的材料参数几乎对颗粒阻尼器的阻尼性能没有影响，此结论与前人的研究结论相似[20]。另一个较为特殊的状态是蹦床状态，这一状态下材料参数对颗粒系统阻尼效果有一定影响，但影响效果差距很小。在其他状态下，材料密度对阻尼效果的影响都比较明显，这符合前人研究得出的颗粒阻尼减振特性与颗粒材料密度关系的结论[21]。剪切模量和恢复系数对阻尼效果的影响较小。静摩擦因数和滚动摩擦因数对处于莱顿弗罗斯特效应和浮力对流两种状态下的颗粒系统影响较小，但对其余状态下颗粒系统的阻尼效果有一定影响，原因可能是这两种状态下颗粒碰撞及摩擦耗能占总耗能的比例较小。

3 结 论

本文基于离散单元法仿真，结合NOPD中颗粒系统的运动状态对阻尼效果进行分析，探究不同振动条件对阻尼性能的影响，并通过正交试验，考察颗粒的材料参数对损耗因子的影响，得到的主要结论如下：

(1)不同激振频率下，颗粒阻尼器表现出最好的阻尼效果时对应的振动强度是不同的。当系统处于低频或中频时，损耗因子的最大值出现在振动强度较小的条件下；而系统处于高频时，损耗因子的最大值出现在振动强度较大的条件下。

(2)颗粒系统表现出不同运动状态时的流变学行为及细观结构导致了阻尼效果的变化，颗粒系统在浮力对流状态时表现出最优的阻尼效果。

(3)当颗粒系统处于不同的运动状态时，颗粒的材料参数对系统阻尼的影响程度是不同的。当颗粒系统处于类固态时，颗粒的材料参数几乎对颗粒阻尼器的阻尼性能没有影响；蹦床状态下材料参数对颗粒系统阻尼效果有一定影响，但影响效果差距很小。在其他状态下，材料密度对阻尼效果的影响都比较明显，而剪切模量和恢复系数对阻尼效果的影响较小；静摩擦因数和滚动摩擦因数对处于莱顿弗罗斯特效应和浮力对流两种状态下的颗粒系统影响较小。

[ 1 ] 鲁正， 吕西林， 闫维明. 颗粒阻尼技术的研究综述[J]. 振动与冲击， 2013, 32(7): 1-7.

LU Zheng, LÜ Xilin, YAN Weiming. A survey of particle damping techology[J]. Journal of Vibration and Shock, 2013, 32(7): 1-7.

[ 2 ] BAJKOWSKI J M, DYNIEWICZ B, BAJER C I. Damping properties of a beam with vacuum-packed granular damper[J]. Journal of Sound and Vibration, 2015, 341: 74-85.

[ 3 ] MICHON G, ALMAJID A, ARIDON G. Soft hollow particle damping identification in honeycomb structures[J]. Journal of Sound and Vibration, 2013, 332(3): 536-544.

[ 4 ] YANG M Y. Development of master design curves for particle impact dampers[D]. The Pennsylvania State University, 2003.

[ 5 ] 夏兆旺， 单颖春， 刘献栋. 基于悬臂梁的颗粒阻尼实验[J]. 航空动力学报， 2007, 22(10): 1737-1741.

XIA Zhaowang, SHAN Yingchun, LIU Xiandong. Experimental research on particle damping of cantilever beam[J]. Journal of Aerospace Power, 2007, 22(10): 1737-1741.

[ 6 ] 周宏伟. 颗粒阻尼及其控制的研究与应用[D]. 南京: 南京航天航空大学, 2008.

[ 7 ] 段勇， 陈前， 林莎. 颗粒阻尼对直升机旋翼桨叶减振效果的试验[J]. 航空学报, 2009, 30(11): 2113-2118.

DUAN Yong, CHEN Qian, LIN Sha. Experiments of vibration reduction effect of particle damping on helicopter rotor blade[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(11): 2113-2118.

[ 8 ] WONG C, DANIEL M, RONGONG J. Energy dissipation prediction of particle dampers[J]. Journal of Sound and Vibration, 2009, 319(1): 91-118.

[ 9 ] XIAO W, LI J, WANG S, et al. Study on vibration suppression based on particle damping in centrifugal field of gear transmission[J]. Journal of Sound and Vibration, 2016, 366: 62-80.

[10] ZHANG K, CHEN T, WANG X, et al. Rheology behavior and optimal damping effect of granular particles in a non-obstructive particle damper[J]. Journal of Sound and Vibration, 2016, 364: 30-43.

[11] MAO K., WANG M Y, XU Z, et al. DEM simulation of particle damping[J]. Powder Technology, 2004, 142(2): 154-165.

[12] MINDLIN R D. Compliance of elastic bodies in contact[J]. Journal of Applied Mechanics, 1949(16): 259-268.

[13] MINDLIN R D, DERESIEWICZ H. Elastic spheres in contact under varying oblique forces[J]. Journal of Applied Mechanics, 1953(20): 327-344.

[14] TSUJI Y, TANAKA T, ISHIDA T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe[J]. Powder Technology, 1992, 71(3): 239-250.

[15] JIANG Z H, WANG Y Y, WU J. Subharmonic motion of granular particles under vertical vibrations[J]. Epl, 2006, 74(3): 417-423.

[16] EHRICHS E, JAEGER H, KARCZMAR G S, et al. Granular convection observed by magnetic resonance imaging[J]. Science, 1995(267): 1632.

[17] ESHUIS P, WEELE K V D, MEER D V D, et al. Granular leidenfrost effect: Experiment and theory of floating particle clusters[J]. Physical Review Letters, 2005( 95): 258001.

[18] YANG B, YICHUNG M. Development of master design curves for particle impact dampers[D]. Doctoral Thesis, The Pennsylvania State University, 2003.

[19] MUJICA N, MELO F. Experimental study of solid-liquid-type transitions in vibrated granular layers and the relation with surface waves[J]. Physical Review E, 2000(63): 011303.

[20] SANCHEZ M, ROSENTHAL G, PUGNALONI L A. Universal response of optimal granular damping devices[J]. Journal of Sound and Vibration, 2012, 331 (20): 4389-4394.

[21] 胡溧. 颗粒阻尼的机理与特性研究[D]. 武汉： 华中科技大学, 2008.