宽频压电振动俘能器的研究现状综述

徐振龙, 单小彪, 谢 涛

(1. 杭州电子科技大学 机械工程学院，杭州 310018；2. 哈尔滨工业大学 机电工程学院，哈尔滨 150001)

近几年，便携式电子设备、微机电系统(MEMS)和无线传感器网络在民用、军事、医疗和工业生产中得到了广泛应用。目前大多数的微电子产品都是利用化学电池提供电能。但由于传统电池存在能量密度小、需要定期更换或充电，以及污染环境等问题，难以满足微电子产品高速发展的需求。

在过去的几年，俘获环境中的能源为微电子产品供能成为一种很有前景的技术，并引起了研究者的强烈关注。环境中的能源有振动能、太阳能、风能、温差能、射频辐射能、噪声等。其中，振动能在日常生活和工程实际中广泛存在，不易受位置、天气等因素的影响，并且具有较高的能量密度，因此越来越多的学者和专家致力于研究将环境中的振动能俘获并转换成电能，作为一种替代能源为微电子产品供能。这种可以将环境中的振动能转化为电能的装置称为振动俘能器(vibration energy harvester)。根据能量转换原理不同，振动俘能器可分为压电式、电磁式、静电式和磁致伸缩式等类型。其中，利用压电材料制成的压电俘能器具有输出能量密度大、结构简单易于加工、无需外部电源、便于实现小型化和集成化等诸多优点，受到国内外的学者普遍关注，具有非常广阔的应用前景。

最初学者们研究的压电俘能器大多数是以单自由度线性系统为基础，其工作频带非常窄，当外界激振频率与系统固有频率相匹配时发电性能最优；当激振频率发生漂移时，发电性能会被迅速削弱。在实际应用中，由于外界环境中的振动频率具有宽频带、随机的特点，压电俘能器的固有频率无法时刻与外界激振频率相匹配，大大限制了其发电性能[1-2]。如何使压电俘能器具有更高的俘能效率、更宽的俘能频带，从而拥有更好的发电性能成为一个普遍关注的问题。

本文将对近几年宽频压电俘能器的国内外研究现状进行综述，主要内容包括压电振动俘能器的工作原理、常用压电材料和工作模式，宽频压电俘能技术，当前研究中存在的问题和不足，以及未来的研究方向。

1 压电振动俘能器

1.1 基本原理

压电俘能是利用环境振动诱导压电结构产生变形，进而引起压电材料内部的正负电荷中心分离，从而产生极化电压，极化电压将驱动极板上的自由电荷定向流动而输出电能，即正压电效应，从而实现将环境中的机械能转换为电能。

1.2 常用的压电材料

压电材料的特性会直接决定压电俘能器的发电性能。目前最常用的压电材料是锆钛酸铅，即PZT压电陶瓷。压电陶瓷具有较大的机电耦合系数和较高的俘能效率，但由于材料本身脆，相对容易碎裂，高频振动环境中容易出现疲劳，因此很少在大应变的换能器中使用[3]；另一种常用的压电材料是聚偏氟乙烯(Polyvinglidene Fluoride, DVDF)。PVDF是一种压电聚合体，虽然它的机电耦合系数小于压电陶瓷，但是它拥有良好的柔韧性、耐老化性[4]，在交变载荷作用下使用寿命更长，因此被广泛用于采集人体运动能[5-6]；1996年美国航空航天局发明了压电纤维复合材料(MFC)[7]，具有柔韧耐用、适用于曲面结构的特点，在d33模式和d31模式均能工作，相对于PZT，容量较低且输出电流较小[8-9]。

1.3 工作模式

根据压电材料的极化方向和所受应力，压电俘能器共有三种工作模式：d31模式、d33模式和d15模式。理论上d15模式俘能效率最高，但是在实际应用中很难有效利用剪切方向的载荷，因此学者们很少将d15模式用于振动俘能。d31模式作用力与极化方向垂直，d33模式作用力的方向与极化方向相同，如图1所示。一般地，d31模式常用于悬臂梁结构中，可利用外界较小的作用力产生较大的形变，提高俘能效率，易于加工， 系统固有频率较低，更易于在低频环境中产生谐振[10]；d33模式采用交叉型电极，加工复杂[11]，尽管机电耦合系数较大，但不容易产生形变，常用于挤压变形中，在大作用力下俘能效率更高[12]。

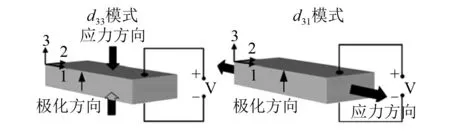
图1 压电材料工作模式 Fig.1 Piezoelectric modes

2 宽频压电俘能技术国内外研究现状

为了改善线性振动俘能器的发电性能，提高环境适应能力，学者们致力于拓宽俘能器的工作频带宽度，达到提高俘能效率的目的。宽频俘能技术主要包括调谐俘能、多模态俘能、非线性俘能、多机制复合俘能和升频转换俘能。

2.1 调谐俘能

调谐俘能即根据环境中振源振动情况，适时调整俘能器的谐振频率，使其与振源振动频率相匹配，提高发电效率，该方法对于振源频率比较单一，存在时变主频率的情况更有效。调谐俘能可通过调整俘能系统的质量或刚度实现。但是从操作方便易于实现角度考虑，学者们大多采用调节系统刚度的方法。

2.1.1 机械调谐

机械调谐是指人为改变俘能器的机械特性，如俘能器结构尺寸、末端质量、或材料特性，从而改变俘能器的有效质量或有效刚度。Shen等[13]设计了一种低频MEMS单晶悬臂梁压电俘能器，在悬臂梁末端附着有硅质量块，质量块有助于降低系统谐振频率，使其与外界激振频率相匹配，提高发电效率；Li等[14]在不改变压电梁外形体积的前提下，将质量块设计成L形(见图2)，充分利用悬臂梁的上部空间，提高了俘能器的能量密度，同时也降低了系统的谐振频率。为了能多次改变系统谐振频率，Wu等[15]利用转动螺钉改变质量块的重心位置，从而改变系统的有效质量，重心离悬臂梁末端越近，系统的有效质量越大，固有频率越低，输出功率越大，俘能器的可调谐振频率范围为130～180 Hz。Leland等[16]提出了一种通过改变压电振子轴向预紧力调节谐振频率的俘能器结构，如图3所示。当施加预负载60 N时，系统的谐振频率可以降低24%，同时机电耦合系数可以提高25%，有效改善了俘能效率。Morris等[17]提出了一种圆盘式压电膜片(PVDF)俘能器，通过预紧螺栓改变压电片径向伸缩量，从而使得系统的谐振频率可在80～235 Hz之间变化。

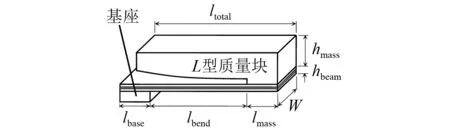
图2 带L形末端质量的压电俘能器[14] Fig.2 Piezoelectric energy harvester (PEH) with the L-shaped proof mass

图3 简支梁压电俘能器[16] Fig.3 A simply supported PEH

2.1.2 磁力调谐

外力会引起结构刚度的改变，从而改变结构的谐振频率。有些学者利用磁铁之间的相互作用力对压电俘能器的谐振频率进行了调节。Challa等[18]提出了一种利用磁力改变俘能器谐振频率的结构，如图4所示，吸引力会降低谐振频率，排斥力会提高谐振频率。通过改变磁铁之间的距离，俘能器的谐振频率变化范围为系统固有频率的±20%，但这种方法的缺点是随着谐振频率的变化，结构阻尼也会发生改变。Reissman等[19]在压电悬臂梁自由端放置一个磁铁，在基座上有一个可上下滑动的磁铁，改变两磁铁之间的竖直距离可改变磁铁之间的吸引力，进而调节俘能器的谐振频率，结构如图5所示。当两个磁铁在垂直方向上的相对位置从0增大到1.5 cm时，谐振频率从99.38 Hz降低到88 Hz。孙晓阳等[20]研究了一种磁力调谐压电俘能器的频率响应特性。

图4 磁力调谐压电俘能器[18] Fig.4 Tunable PEH

图5 磁力调谐压电俘能器[19] Fig.5 Tunable PEH

2.1.3 电学调谐

电学调谐主要是利用压电作动器和容性负载改变俘能器的结构刚度，实现调谐俘能。Roundy等[21]提出了利用压电作动器进行持续主动调谐的方法。俘能器具有两个电极，一个用于调谐，一个用于俘能。当施加5 V调谐电压时，系统的谐振频率从67 Hz降为64.5 Hz。但是输出功率仅为82 μW，远低于作动器消耗的功率(440 μW)。研究表明，持续主动调谐不会带来俘能器输出功率的净增量。Lallart等[22]搭建了一个集检测和驱动于一体的自调谐压电俘能系统，如图6所示。文中采用压电片检测基座振动频率与压电梁变形之间的相位差，将压电元件与振荡电路间歇性接通，有效改变压电梁的刚度，该方法使系统的带宽由4.1 Hz增大到17 Hz。Wu等[23]提出一种实时自动调谐俘能系统，微控制器通过采样振源频率，改变系统的容性负载，从而调节俘能器的谐振频率。Cammarano等[24]利用电容和电感元件调节俘能系统的谐振频率，俘能器在最优阻抗下的输出功率是单纯连接最优电阻的输出功率的三倍。考虑到压电俘能系统中的阻抗会影响系统的电气阻尼，而纯电阻会降低俘能效率，因此，学者们大多利用容性负载调整俘能器的谐振频率。

总之，调谐俘能大多是改变系统的阻尼或刚度，改变质量块的方法不适用于自调谐俘能，电气阻尼可通过改变系统的阻抗实现调谐，自调谐俘能器集合压电驱动与频率检测于一体，但是会消耗一部分能量。

图6 自调谐压电俘能器[22] Fig.6 Self-tuned PEH

2.2 多模态俘能

多模态俘能是利用俘能器的多阶振动模态发电，实现宽频俘能。压电俘能器阵列是一种常见的多模态俘能器，通常是由多个具有不同谐振频率的线性压电俘能器组合而成，整体的频带宽度由各个压电振子的谐振频率叠加而成。刘景全等[25]设计并研制了一种MEMS悬臂梁压电俘能器阵列，压电振子之间串联连接，实验测得俘能器阵列的输出功率为3.98 μW，输出直流电压为3.93 V，满足低功耗传感器网络的供能需求。杨同青等[26]设计了一种压电圆形膜片俘能器阵列，进行了实验研究。俘能器阵列尽管有效地拓宽了俘能频带，但是使用了复杂的接口电路；此外，由于在某一特定频率下，阵列仅有一个压电振子发生共振，而其他压电振子几乎不发电，因此俘能器阵列的能量密度很低。

多模态俘能器的另一种常见形式是耦合振子结构，利用系统的多阶振动模态俘获振动能，尤其是前两阶振动模态。众所周知，俘能器在谐振频率处输出功率最大，如果前两阶谐振频率比较接近，则俘能器的俘能频带将得到有效拓宽，俘能效率也会大幅提升。Roundy等[27]提出利用多个附加质量搭建多自由度弹簧-质量-阻尼系统，拓宽俘能频带的想法。Yang等[28]将两个谐振频率相近的悬臂梁压电振子在自由端用弹簧连接，搭建了一个两自由度压电俘能器，结构如图7所示，通过优化结构参数可实现宽频俘能。Aldraihem等[29]在悬臂梁压电俘能器和基座之间增加了一个弹簧-质量系统，用于增大压电振子上的应变，增加输出功率。同时，弹簧-质量系统的谐振频率在经过仔细调整后，还可以拓宽俘能器的俘能频带。刘景全等[30]在传统的悬臂梁压电俘能器自由端连接一个非线性弹簧振子，构成一个两自由度压电俘能器，有效改善了俘能效率。黄震宇等[31]在压电悬臂梁上附着多个谐振子制成多模态压电俘能器，在相同激励环境下，该俘能器比传统的悬臂梁压电俘能器的输出功率提高了82%。Tang等[32]将压电悬臂梁末端质量换成磁铁，与一个磁振子通过磁力耦合，形成一个磁振子压电俘能器，如图8所示。在外界激励作用下，磁振子的一部分振动能会转移到压电振子上变成电能，因此该俘能器的输出功率相比单自由度压电俘能器提高了41%，带宽提高了100%。

图7 多模态压电俘能器[28] Fig.7 Elastically connected PEH

图8 磁振子压电俘能器[32] Fig.8 PEH with magnetic oscillator

2.3 非线性俘能

近几年，非线性压电振动俘能技术受到学者们越来越多的关注。相对于线性俘能器，非线性压电俘能器具有频带宽度更广，发电效率更高的特点。俘能器的非线性主要指非线性刚度和非线性压电耦合。非线性压电耦合由压电材料的加工工艺、材料特性等决定。相对而言，非线性刚度更易于实现。目前引入非线性刚度的方式主要有三种：非线性磁力、机械结构弹性大应变和分段线性结构[33]。

2.3.1 非线性磁力耦合

起初磁力被用于改变俘能器刚度，从而调节谐振频率，后来研究表明磁力引起的非线性对拓宽频带、提高俘能效率也有很重要的作用。Stanton等[34]提出了一种单稳态非线性压电俘能装置，如图9所示，即俘能装置在压电梁末端附有永磁铁，与固定永磁铁之间有相互作用的非线性磁力。沿悬臂梁轴向改变固定磁铁与末端磁铁的距离，可以分别实现硬弹簧和软弹簧系统。实验证明，这种非线性结构不仅有效拓宽频带，而且具有更好的发电性能。Sebald等[35-36]对压电俘能器Duffing振子模型进行了理论和实验研究。在俘能频带宽度相同的情况下，非线性俘能器的输出功率是线性俘能器的16.5倍。系统在最大输出功率处存在两个稳态调和解，为了获得更大的输出功率和更宽的频带，可以使用快速脉冲扰动使系统实现从低能解到高能解的跃迁。双稳态压电俘能器能够在微弱激励下的发生大幅、宽频周期或非周期振动，从而在非共振状态下获得结构大变形，提高发电效率。Lin等[37]研究了谐振激励下双稳态压电振子耦合非线性磁力的发电特性，在谐振频率处，输出性能与线性压电俘能器无异；在非共振频带，磁力引发压电悬臂梁混沌振动，提高了振幅和发电性能，从而拓宽了俘能器的工作频带。Ferrari等[38]建立了双稳态悬臂梁的Duffing型方程，利用数值方法计算了悬臂梁在白噪声激励下的随机共振位移响应，并进行了实验研究，然而文中只研究了非线性项对双稳态现象的影响，并未给出双稳态压电发电系统的响应特性，压电俘能振子结构示意图如图10所示。

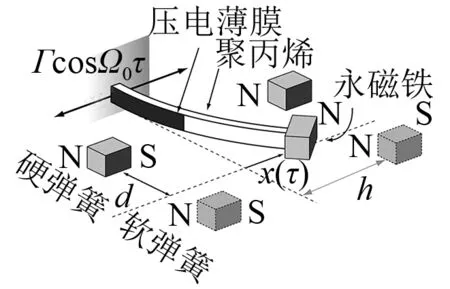
图9 单稳态非线性压电 俘能器[34] Fig.9 Monostable nonlinear PEH

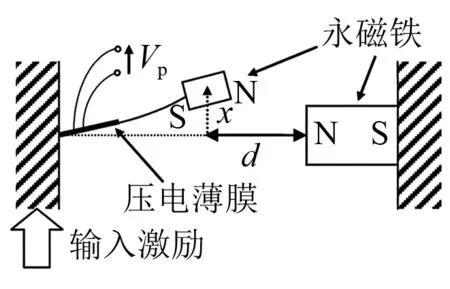
图10 双稳态非线性压电 俘能器[38] Fig.10 Bistable nonlinear PEH

2.3.2 非线性大应变

部分学者利用机械结构的非线性应变引入非线性弹簧刚度：Hajati等[39]利用MEMS固支梁的拉伸应变引入非线性刚度，提出了一种超宽频压电俘能器，如图11所示。该压电俘能器的频带宽度和能量密度均比以往报道的压电俘能器高出一个数量级。Arrieta等[40]对双稳态碳纤维板压电俘能器的频率响应进行了实验研究。通过慢扫频激励实验，发现具有宽频的非线性大振幅振荡：1/2亚谐振荡，极限环振荡、混沌运动和间歇振荡。Sneller等[41]提出了一种屈曲梁结构非线性压电俘能器，如图12所示。梁的中部放有质量块。屈曲梁结构在简谐激励下具有跳跃现象，系统存在两个平衡位置。实验表明，附加质量块有助于拓宽俘能器的工作频带，系统的跳跃动作使得系统产生大振幅振荡，系统的发电量提高。此外，增加附加质量有助于降低诱发跳跃的激振力阈值。Cottone等[42]对屈曲梁结构压电俘能器在宽频带随机激励条件下的发电特性做了相关研究，其输出功率是非屈曲状态下的10多倍。Friswell等[43]利用附加质量给竖直放置悬臂梁施加轴向负载实现双稳态。这种结构可用于低频环境俘能，但不容易激发出势阱间振荡。

图11 超宽频压电俘能器[39] Fig.11 Ultra-wide bandwidth PEH

图12 屈曲梁结构非线性 压电俘能器[41] Fig.12 Post-buckled PEH

2.3.3 分段线性结构

有学者提出利用俘能器与限位器(stopper)之间的碰撞改变系统的等效刚度，获得分段线性恢复力，这种行为表现为全局的非线性行为，类似于非线性硬弹簧系统，正向扫频时具有拓宽俘能频带的效果。Mak等[44]对一种具有突起止动块的悬臂梁式压电俘能器进行了研究，该俘能器结构示意图如图13所示。他们对俘能器进行了理论建模，并利用数值仿真分析了俘能器与止动块之间空隙、止动块位置对悬臂梁振动行为和输出电压的影响。Halim等[45]在具有弹性基底的两自由度压电俘能器基础上，改变基座结构，使俘能器在振动过程中与基座发生碰撞，提出了一种分段线性两自由度压电俘能器，如图14所示。该俘能器的带宽是相同条件下无碰撞两自由度压电俘能器的2.5倍。此时，基座类似于限位器，碰撞行为有效地拓宽了频带宽度。

图14 两自由度分段线性 压电俘能器[45] Fig.14 2DOF piecewise linear PEH

近两年国内在非线性压电俘能器方面的研究突飞猛进，主要是集中于创新构型设计和非线性俘能机理研究。Jiang等[46]对双稳态压电俘能器在随机激励下的发电特性进行了理论建模，研究了小幅激励和大幅激励下系统参数对输出电压和输出功率的影响。陈仲生等[47]，孙舒等[48]，崔岩等[49]和唐炜等[50]基于典型结构的磁力耦合非线性压电俘能器的非线性特性进行了研究。姚明辉等[51]和周生喜等[52]对固定磁铁的空间布置进行了改变。沈威等[53]设计了一种新型阵列式压电磁耦合俘能器，该俘能器将压电悬臂梁阵列式排布并在系统中引入非线性磁力。冷永刚等[54]提出了弹性支撑磁力耦合双稳态压电俘能器，在低强度激励条件下也能处于双稳态振荡，提高了系统的俘能效率。Fan等[55]提出了一种磁力耦合双稳态压电俘能器，建立了集中参数数学模型，对俘能器的发电特性进行了实验研究。李海涛等[56]基于屈曲梁式双稳态压电俘能器建立了系统动力学模型并且分析了系统的同宿分岔和混沌等非线性动力学行为。Xu等[57]提出了一种悬臂梁驱动铙钹型压电俘能器，具有低频大功率特性，由于悬臂梁与铙钹端面非线性接触导致输出功率具有非线性，通过增加悬臂梁末端质量可以增大悬臂梁位移，从而降低俘能器的非线性跳跃点，这使得系统在低激振加速度环境下可获得较高的发电性能。Liu等[58]提出一种新型两自由度分段线性压电俘能器，对其前两阶振动模态下的发电特性进行了理论和实验研究。实验结果表明，该俘能器前两阶模态下的频带宽度是两自由度线性俘能器的4.78倍。刘会聪等[59]曾对一种利用俘能振子与基座碰撞实现宽频带的分段线性微型压电俘能器开展研究。

2.4 多机制复合俘能

多机制复合俘能器指俘能器包含压电俘能、电磁俘能、静电俘能等多种俘能机制。鉴于压电俘能器适用于高频环境下发电，电磁俘能器适用于低频环境发电，两者都具有较高的机电耦合系数，都不需要外接电源，因此，压电电磁复合俘能装置的相关研究最多。由于系统电气阻尼的增加，这种复合俘能装置的工作频带宽度得以拓宽。

Challa等[60]提出一种悬臂梁结构压电电磁复合俘能装置，结构如图15所示，该俘能器由压电悬臂梁、永磁铁(做末端质量块)和感应线圈组成。实验测得谐振频率为21.6 Hz时，复合装置最大输出功率为332 μW，而优化后的单独压电和单独电磁发电最大输出功率分别为257 μW和244 μW。Tadesse等[61]提出了一种多模态压电电磁复合俘能装置。锥形悬臂梁上下表面粘有三组压电片，采用电气并联形式，主要研究系统前两阶模态的性能。Karami等[62]提出一种新型的压电电磁复合非线性俘能装置，利用两个相互排斥的磁铁产生非线性磁力，扩宽了俘能器的频带，提高了发电性能。Mahmoudi等[63]将压电固支梁和磁悬浮结构相结合，设计了一个具有非线性刚度的压电电磁复合俘能器，结构如图16所示。

图15 压电电磁复合俘能器[60] Fig.15 Hybrid energy harvester (HEH)

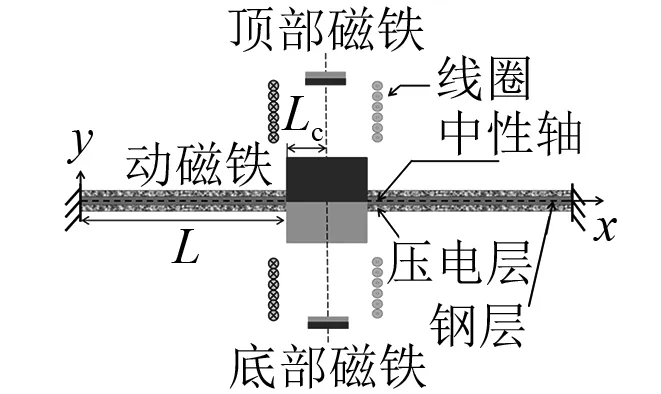
图16 压电电磁复合非线性 俘能器[63] Fig.16 Nonlinear HEH

目前，国内研究者的精力主要集中于单一俘能机制的理论研究和构型设计，有关压电电磁复合俘能的相关研究刚刚起步。Sang等[64]通过变换磁铁与线圈的空间分布形式提出四种梁式压电电磁复合俘能器，在激振加速度为0.4 g、激振频率为50 Hz条件下，复合俘能器输出功率为1.7 mW，比单独的电磁俘能器输出功率提高了81.4%。Li等[65]研究了机电耦合系数对复合俘能器性能的影响，不同负载和激振频率下的输出响应，并与单独压电和单独电磁俘能器进行了对比。Yu等[66]设计了一种适用于低频小振幅激励环境下的MEMS压电电磁复合俘能器，建立了集中参数数学模型，并进行了有限元仿真和实验研究。谢涛课题组[67-69]对压电电磁复合俘能进行了持续的研究，从构型设计、理论建模、有限元仿真和实验验证等多个方面进行了比较全面的研究。

2.5 升频转换俘能

环境中的一些振源振动具有低频(<30 Hz)大振幅的特点，如人体运动，而微型压电俘能器的谐振频率普遍较高，有的高达几千赫兹，在这种环境下振动俘能器的俘能效率受到很大限制。为此，有学者提出了升频转换的俘能机制。升频转换是利用惯性质量的低频运动激发压电俘能器的高频谐振，提高俘能器的俘能效率，降低俘能器对外界激振频率的依赖性。

2.5.1 接触式

接触式升频的原理是：低频振子从外部振源俘获振动能，通过机械碰撞传递给高频振子，转换成高频振子的振动能，然后变成电能输出。这种俘能机制最初是由Umeda等[70]提出并应用于压电俘能：一个钢球在距离压电振子一定高度处自由落下，撞击压电振子后反弹，当两者分离后，压电振子做自由振动并输出电荷。Rastegar等[71]提出了适用于超低频(0.2～0.5 Hz)振动或小角度晃动平台的两级俘能装置的概念，结构原理图见图17，当初级振动单元(质量块)撞击二级振动单元(压电悬臂梁)时，激发悬臂梁的高频自由振动。Galchev等[72]提出了一种适用于低频(<30 Hz)非周期振动环境的升频转换压电俘能装置，装置中的惯性质量块与压电振子因磁力作用结合在一起，当质量块与磁铁瞬间分离时，激发压电振子的高频振动，将环境中的振动能转化为电能Wei等[73]开发了一种升频转换人体运动俘能器，可以将滑块的轴向运动转换成压电梁末端的横向脉冲力，减小了俘能器的体积，提高了能量密度。Liu等[74]和秦利锋等[75]也对此类压电俘能器进行了研究。Xu等[76]对碰撞升频式压电电磁复合俘能器开展了理论和实验研究，指出碰撞过程中存在的次碰撞现象，并分析了输出电信号的频率成分。

2.5.2 非接触式

非接触式升频是指低频振子与高频振子之间有相互作用力，在不接触元件的情况下传递振动能，避免了因撞击引起的能量损失和结构可靠性问题。最常见的是利用磁铁之间的吸引力或排斥力激发压电俘能振子的高频振动。Wickenheiser等[77]利用压电悬臂梁自由端的磁铁与铁磁材料之间的吸引力实现升频转换，结构如图18所示，在0.1倍基频的简谐激励下，该俘能器的输出功率是传统线性悬臂梁压电俘能器的8个数量级。Tang等[78]设计了一种微型的磁力升频双稳态压电俘能装置，利用悬浮磁铁与悬臂梁末端磁铁之间的排斥力激发压电振子的高频振动。当激励加速度为1 g时，频带宽度为12 Hz，平均输出功率10 μW。Pillatsch等[79]提出了一种可用来俘获转动能的压电俘能器，利用磁力作用将偏心轮的转动能转换成压电悬臂梁的高频振动，并进行了人体运动实验研究。

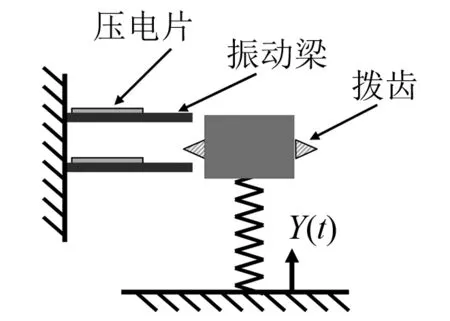
图17 碰撞升频压电 俘能器[71] Fig.17 Two-stage frequency up-conversion PEH

图18 磁激励升频压电 俘能器[77] Fig.18 Non-contact frequency up-conversion PEH

Jung等[80]利用屈曲梁的突跳特性实现非接触式升频转换，当屈曲梁受到高于加速度阈值的低频激励时，突跳会产生较大的脉冲加速度，激发压电悬臂梁的高频振动。但是这种结构的加速度阈值较大，在激励加速度较小的环境下难以实现升频转换，为此，Han等[81]设计了一种双梁式的升频俘能装置，将屈曲梁固定在柔性基座上，大大降低了激发突跳转换的加速度阈值，实验测得，当屈曲梁结构两端固定于乳胶基座上时，加速度阈值为0.5 g。

升频转换俘能技术将激振频率和俘能器的谐振频率解耦，当激振频率低于俘能器的谐振频率时，俘能器的发电性能不易受激振频率变化的影响。这种技术尤其适用于MEMS压电俘能器在低频(<30 Hz)激励下的俘能，因为MEMS俘能装置的谐振频率过高，调谐俘能和多模态俘能技术几乎难以实现宽频俘能。

3 当前研究中存在的问题和不足

综合国内外研究现状，压电振动俘能器的宽频俘能技术是当前的研究热点，尤其是磁力耦合压电俘能技术，但是当前研究中还存在一些问题和不足：

(1)可调谐压电振动俘能器的研究大多只是从结构原理角度进行了可行性研究，一些机械调谐和磁力调谐俘能器是通过手动实现离散调谐，显然在工程应用中这是不可取的。从自动化角度出发，利用传感器对振源频率进行监测并通过外部控制电路实现俘能器的主动调谐更具有实际意义，但这会增加系统的功耗。因此，在实现机电系统自动化控制和降低系统功耗之间如何平衡是研究者们需要解决的问题。

(2)现有的多模态俘能器侧重研究其在一段连续振动频率区间上的发电特性。环境中有些振源存在两个或多个较稳定的、离散的振动频率，例如暖通空调通风口的振动频率包括21.8 Hz、29 Hz和127.3 Hz[82]。此时，传统的多模态俘能器难以兼顾多个离散的振动频率，发电性能难以达到最优。针对此类振源振动特点，如何优化多模态俘能器结构，提高俘能效率是值得思考的问题。

(3)尽管非线性俘能器在扫频过程中表现出宽频特性，但是大多需要很大的激励加速度。在小幅激励环境下，非线性俘能器的输出功率频率响应与线性俘能器的类似，优势不明显。由于非线性俘能器在一定频率范围和激励条件下具有多解，如何保持非线性俘能器(尤其是双稳态或多稳态系统)稳定地处于高能轨道值得研究。如果通过外部电路监测其振动特性，并通过实施激励维持在高能轨道，需要兼顾电路功耗问题；也可以进一步探索此类俘能器更加准确的理论模型，从而通过优化结构参数和激励条件达到相同的目的。有关耦合双稳态俘能器发电机理和动力学行为的研究还比较少见。当系统输出混动或非周期电压信号时，如何设计俘能电路以提高俘能器的能量转换效率具有重要意义。此外，目前尚且缺少公认的针对非线性俘能器发电性能的评价指标，当俘能器耦合外部俘能电路后会进一步使问题复杂化。此类俘能器的非线性动力学行为一直是学者们研究的难点和热点问题[83-84]。

(4)压电电磁复合俘能器通过增加系统的电气阻尼达到拓宽频带的目的。但是目前大多学者采用简化的线性弹簧-质量-阻尼模型评估压电电磁复合俘能器的发电特性。有的将电磁机电耦合系数或电磁阻尼线性化，有的忽略机电耦合系数对系统刚度的影响。过分简化模型不利于全面深入地研究结构参数和外部负载对发电特性的影响规律，难以为俘能器的优化设计提供有效的理论依据。复合机制相对单一机制的优势及其适用条件有待进一步明确。压电部分产生的电信号具有高电压低电流，而电磁部分产生的电信号具有低电压高电流，如何将两种电信号高效地管理、收集和存储是一直困扰学者们的问题。

(5)目前学者们在建立升频转换俘能器的理论模型时简单地认为碰撞过程是弹性、不完全弹性或者完全非弹性碰撞，且只考虑了一阶振动模态，而实验结果表明，碰撞后压电振子出现了更高次谐振，如何从理论模型的角度解释压电振子的行为还有待研究。现有的升频转换俘能器的低频振子大多仅用于激发俘能振子的高频振动，考虑低频振子同时用于俘能的研究还很少见，低频振子直接参与发电是否有利于提高整体俘能效率还不明确。

4 未来的研究方向

结合前文所述，笔者认为宽频压电俘能器未来可能的研究方向大致有以下几个方面：

(1)机电耦合数学模型的完善。随着俘能器结构的不断创新，简单的数学模型难以准确有效地描述俘能器复杂的动力学行为和电学响应，比如双稳态系统在随机激励条件下的响应。建立更加精准的机电耦合数学模型有利于俘能器发电特性的评估和结构的优化设计。

(2)多种宽频措施的有机组合。前面所总结的各种宽频方式具有各自不同的适用场合和优势，合理利用多种宽频手段，克服单一宽频机制的缺陷，取长补短，提高俘能器的整体俘能效率，扩展俘能器的应用环境。

(3)更加高效的俘能电路。压电俘能器产生的交流电容易受振源和自身结构的影响，很难直接为负载供电。为了给负载提供稳定、持续的电能，需要设计开发具有更高能量转换、收集效率的俘能电路。

(4)面向具体应用进行结构设计。随着俘能器相关理论研究的成熟，最终必然走向工程实际应用。针对具体的应用背景，结合振源特点(如人体、道路、车辆等)和负载特点(如便携式电子设备、无线传感器节点等)，优化设计满足应用需求的宽频压电俘能器。

(5)改进加工工艺和封装技术。随着低功耗微电子技术与微机械加工技术的发展，俘能器逐步向微型化、集成化方向发展。不断改进微型压电俘能器的加工工艺和封装技术，以提高俘能器的稳定性、兼容性和工作寿命，提高俘能效率，同时降低生产成本。

5 结 论

本文对宽频压电俘能技术的研究现状进行了综述，总结了当前研究中的问题和不足，提出了未来可能的研究方向。当前研究者的主要工作集中于对压电振动俘能器俘能机理、构型设计和宽频俘能技术的研究，俘能器距离工程实际应用尚有一定的距离。今后研究工作应充分考虑实际应用背景，对压电振动俘能系统的结构参数和电学参数进行优化设计，以提高其环境适应能力和俘能效率。压电振动俘能技术为低功耗微电子产品提供了一种稳定、安全、长久的新供能方式，具有良好的应用前景。

[ 1 ] RAMLAN R, BRENNAN M J, MACE B R, et al. Potential benefits of a non-linear stiffness in an energy harvesting device[J]. Nonlinear Dynamics, 2010, 59(4)： 545-558.

[ 2 ] COTTONE F, VOCCA H, GAMMAITONI L. Nonlinear energy harvesting[J]. Physical Review Letters, 2009, 102(8)：080601.

[ 3 ] FLYNN A M, SANDERS S R. Fundamental limits on energy transfer and circuit considerations for piezoelectric transformers[J]. IEEE Transactions on Power Electronics, 2002, 17(1)： 8-14.

[ 4 ] KIM H S, KIM J H, KIM J. A review of piezoelectric energy harvesting based on vibration[J]. International Journal of Precision Engineering and Manufacturing, 2011, 12(6)： 1129-1141.

[ 5 ] SUN C L, SHI J, BAYERL D J, et al. PVDF microbelts for harvesting energy from respiration[J]. Energy and Environmental Science, 2011, 4(11)： 4508.

[ 6 ] LEE M, CHEN C Y, WANG S H, et al. A hybrid piezoelectric structure for wearable nanogenerators[J]. Advanced Materials, 2012, 24(13)： 1759-1764.

[ 7 ] WILKIE W K, BRYANT R G, HIGH J W, et al. Low-cost piezocomposite actuator for structural control applications[C]∥ Proceedings of SPIE, Newport Beach, 2000： 323-334.

[ 8 ] SCHÖNECKER A J, DAUE T, BRÜCKNER B, et al. Overview on macro fiber composite applications[C]∥ Proceedings of SPIE, San Diego, CA, 2006： 61701K-61701K-61708.

[ 9 ] SODANO H A, PARK G, INMAN D J. An investigation into the performance of macro-fiber composites for sensing and structural vibration applications[J]. Mechanical Systems and Signal Processing, 2004, 18(3)： 683-697.

[10] ROUNDY S, WRIGHT P K, RABAEY J. A study of low level vibrations as a power source for wireless sensor nodes[J]. Computer Communications, 2003, 26(11)： 1131-1144.

[11] KIM S B, PARK H, KIM S H, et al. Comparison of MEMS PZT cantilevers based on d31 and d33 modes for vibration energy harvesting[J]. Journal of Microelectromechanical Systems, 2013, 22(1)： 26-33.

[12] BAKER J, ROUNDY S, WRIGHT P. Alternative geometries for increasing power density in vibration energy scavenging for wireless sensor networks[C]∥ Proceedings of 3rd International Energy Conversion Engineering Conference, San Francisco, California, 2005： 1-12.

[13] SHEN D, PARK J H, AJITSARIA J, et al. The design, fabrication and evaluation of a MEMS PZT cantilever with an integrated Si proof mass for vibration energy harvesting[J]. Journal of Micromechanics and Microengineering, 2008, 18(5)： 055017.

[14] LI W G, HE S Y, YU S D. Improving power density of a cantilever piezoelectric power harvester through a curved L-shaped proof mass[J]. IEEE Transactions on Industrial Electronics, 2010, 57(3)： 868-876.

[15] WU X M, LIN J H, KATO S, et al. A frequency adjustable vibration energy harvester[C]∥ Proceedings of PowerMEMS, Sendai, 2008： 245-248.

[16] LELAND E S, WRIGHT P K. Resonance tuning of piezoelectric vibration energy scavenging generators using compressive axial preload[J]. Smart Materials and Structures, 2006, 15(5)： 1413-1420.

[17] MORRIS D J, YOUNGSMAN J M, ANDERSON M J, et al. A resonant frequency tunable, extensional mode piezoelectric vibration harvesting mechanism[J]. Smart Materials and Structures, 2008, 17(6)： 065021.

[18] CHALLA V R, PRASAD M G, SHI Y, et al. A vibration energy harvesting device with bidirectional resonance frequency tunability[J]. Smart Materials and Structures, 2008, 17(1)： 015035.

[19] REISSMAN T, WOLFF E M, GARCIA E. Piezoelectric resonance shifting using tunable nonlinear stiffness[C]∥ Proceedings of SPIE, San Diego, CA, 2009： 72880G-72880G-72812.

[20] 孙晓阳，王佩红，王卓，等. 一种可调频的压电式振动能量采集器[J]. 微纳电子技术，2014，51(8)： 518-522.

SUN Xiaoyang, WANG Peihong, WANG Zhuo, et al. Apiezoelectric vibration energy harvester with the adjustable frequency[J]. MEMS and Sensors, 2014, 51(8)： 518-522.

[21] ROUNDY S, ZHANG Y. Toward self-tuning adaptive vibration-based microgenerators[C]∥ Proceedings of SPIE, Bellingham, WA, 2005： 373-384.

[22] LALLART M, ANTON S R, INMAN D J. Frequency self-tuning scheme for broadband vibration energy harvesting[J]. Journal of Intelligent Material Systems and Structures, 2010, 21(9)： 897-906.

[23] WU W J, CHEN Y Y, LEE B S, et al. Tunable resonant frequency power harvesting devices[C]∥ Proceedings of SPIE, San Diego, CA, 2006： 61690A-61690A-61698.

[24] CAMMARANO A, BURROW S G, BARTON D A W, et al. Tuning a resonant energy harvester using a generalized electrical load[J]. Smart Materials and Structures, 2010, 19(5)： 055003.

[25] LIU J Q, FANG H B, XU Z Y, et al. A MEMS-based piezoelectric power generator array for vibration energy harvesting[J]. Microelectronics Journal, 2008, 39(5)： 802-806.

[26] WANG W, YANG T Q, CHEN X R, et al. Vibration energy harvesting using a piezoelectric circular diaphragm array[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2012, 59(9)： 2022-2026.

[27] ROUNDY S, LELAND E S, BAKER J, et al. Improving power output for vibration-based energy scavengers[J]. IEEE Pervasive Computing, 2005, 4(1)： 28-36.

[28] YANG Z T, YANG J S. Connected vibrating piezoelectric bimorph beams as a wide-band piezoelectric power harvester[J]. Journal of Intelligent Material Systems and Structures, 2009, 20(5)： 569-574.

[29] ALDRAIHEM O, BAZ A. Energy harvester with a dynamic magnifier[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(6)： 521-530.

[30] YANG B, LIU J Q, TANG G, et al. A generator with nonlinear spring oscillator to provide vibrations of multi-frequency[J]. Applied Physics Letters, 2011, 99(22)： 223505.

[31] LIU H L, XU T Z, HUANG Z Y, et al. Parametric design for a piezoelectric cantilever carrying oscillators to harvest multi-frequency vibration energy[J]. International Journal of Applied Electromagnetics and Mechanics, 2013, 41(4)： 389-405.

[32] TANG L H, YANG Y W. A nonlinear piezoelectric energy harvester with magnetic oscillator[J]. Applied Physics Letters, 2012, 101(9)：094102.

[33] DAQAQ M, MASANA R, ERTURK A，et al. On the role of nonlinearities in vibratory energy harvesting: a critical review and discussion[J]. Applied Mechanics Reviews, 2014, 66(4)： 040801-040801-23

[34] STANTON S C, MCGEHEE C C, MANN B P. Reversible hysteresis for broadband magnetopiezoelastic energy harvesting[J]. Applied Physics Letters, 2009, 95(17)： 174103.

[35] SEBALD G, KUWANO H, GUYOMAR D, et al. Simulation of a duffing oscillator for broadband piezoelectric energy harvesting[J]. Smart Materials and Structures, 2011, 20(7)： 075022.

[36] SEBALD G, KUWANO H, GUYOMAR D, et al. Experimental duffing oscillator for broadband piezoelectric energy harvesting[J]. Smart Materials and Structures, 2011, 20(10)： 102001.

[37] LIN J T, LEE B, ALPHENAAR B. The magnetic coupling of a piezoelectric cantilever for enhanced energy harvesting efficiency[J]. Smart Materials and Structures, 2010, 19(4)： 045012.

[38] FERRARI M, FERRARI V, GUIZZETTI M, et al. Improved energy harvesting from wideband vibrations by nonlinear piezoelectric converters[J]. Sensors and Actuators A-Physical, 2010, 162(2)： 425-431.

[39] HAJATI A, KIM S G. Ultra-Wide Bandwidth piezoelectric energy harvesting[J]. Applied Physics Letters, 2011, 99(8)： 083105.

[40] ARRIETA A F, HAGEDORN P, ERTURK A, et al. A piezoelectric bistable plate for nonlinear broadband energy harvesting[J]. Applied Physics Letters, 2010, 97(10)： 104102.

[41] SNELLER A J, CETTE P, MANN B P. Experimental investigation of a post-buckled piezoelectric beam with an attached central mass used to harvest energy[C]∥ Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, Durham, North Carolina, 2011： 497-509.

[42] COTTONE F, GAMMAITONI L, VOCCA H, et al. Piezoelectric buckled beams for random vibration energy harvesting[J]. Smart Materials and Structures, 2012, 21(3)： 035021.

[43] FRISWELL M I, ALI S F, BILGEN O, et al. Non-linear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass[J]. Journal of Intelligent Material Systems and Structures, 2012, 23(13)： 1505-1521.

[44] MAK K H, MCWILLIAM S, Popov A A，et al. Performance of a cantilever piezoelectric energy harvester impacting a bump stop[J]. Journal of Sound and Vibration, 2011, 330(25)： 6184-6202.

[45] HALIM M A, PARK J Y. Low frequency vibration energy harvester using stopper-engaged dynamic magnifier for increased power and wide bandwidth[J]. Journal of Electrical Engineering and Technology, 2016, 11(3)： 709-716.

[46] JIANG W A, CHEN L Q. Snap-through piezoelectric energy harvesting[J]. Journal of Sound and Vibration, 2014, 333(18)： 4314-4325.

[47] 陈仲生，杨拥民. 悬臂梁压电振子宽带低频振动能量俘获的随机共振机理研究[J]. 物理学报，2011，60(7)： 074301.

CHEN Zhongsheng, YANG Yongmin. Stochastic resonance mechanism for wideband and low frequency vibration energy harvesting based on piezoelectric cantilever beams[J]. Acta Physica Sinica, 2011, 60(7)： 074301.

[48] 孙舒，曹树谦. 双稳态压电悬臂梁发电系统的动力学建模及分析[J]. 物理学报，2012，61(21)： 210505.

SUN Shu, CAO Shuqian. Dynamic modeling and analysis of a bistable piezoelectric cantilever power generator system[J]. Acta Physica Sinica, 2012, 61(21)： 210505.

[49] 崔岩，王飞，董维杰，等. 非线性压电式能量采集器[J]. 光学 精密工程，2012，20(12)： 2737-2743.

CUI Yan, WANG Fei, DONG Weijie, et al. Nonlinear piezoelectric energy harvester[J]. Optics and Precision Engineering, 2012, 20(12)： 2737-2743.

[50] 唐炜，王小璞，曹景军. 非线性磁式压电振动能量采集系统建模与分析[J]. 物理学报，2014，63(24)： 240504.

TANG Wei, WANG Xiaopu, CAO Jingjun. Modeling and analysis of piezoelectric vibration energy harvesting system using permanent magnetics[J]. Acta Physica Sinica, 2014, 63(24)： 240504.

[51] 姚明辉，李印波，张伟. 纵向辅磁双稳态压电悬臂梁非线性动力学[J]. 北京工业大学学报，2015，41(11)： 1756-1760.

YAO Minghui, LI Yinbo, ZHANG Wei. Nonlinear dynamicson auxiliary magnet for a bistable piezoelectric cantilever beam[J]. Journal of Beijing University of Technology, 2015, 41(11)： 1756-1760.

[52] 周生喜，曹军义，Erturk A，等. 压电磁耦合振动能量俘获系统的非线性模型研究[J]. 西安交通大学学报，2014，48(1)： 1-6.

ZHOU Shengxi, CAO Junyi, Erturk A, et al. Nonlinear model for piezoelectric energy harvester with magnetic coupling[J]. Journal of Xi’an Jiaotong University, 2014, 48(1)： 1-6.

[53] 沈威，陶孟仑，陈定方，等. 阵列式压电磁耦合能量收集器的建模与仿真分析[J]. 武汉理工大学学报，2015，37(2)： 116-120.

SHEN Wei, TAO Menglun, CHEN Dingfang, et al. Modeling and simulation of piezomagnetoelastic energy harvester with beam array[J]. Journal of Wuhan University of Technology, 2015, 37(2)： 116-120.

[54] 高毓璣，冷永刚，范胜波，等. 弹性支撑双稳压电悬臂梁振动响应及能量采集研究[J]. 物理学报，2014(9)： 62-74.

GAO Yuji, LENG Yonggang, FAN Shengbo, et al. Studies on vibration response and energy harvesting of elastic-supported bistable piezoelectric cantilever beams[J]. Acta Physica Sinica, 2014(9)： 62-74.

[55] FAN K Q, CHAO F B, ZHANG J G, et al. Design and experimental verification of a bi-directional nonlinear piezoelectric energy harvester[J]. Energy Conversion and Management, 2014, 86： 561-567.

[56] 李海涛，秦卫阳. 双稳态压电能量获取系统的分岔混沌阈值[J]. 应用数学和力学，2014，35(6)： 652-662.

LI Haitao, QIN Weiyang. Bifurcation and chaos thresholds of bistable piezoelectric vibration energy harvesting systems[J]. Applied Mathematics and Mechanics, 2014, 35(6)： 652-662.

[57] XU C D, REN B, LIANG Z, et al. Nonlinear output properties of cantilever driving low frequency piezoelectric energy harvester[J]. Applied Physics Letters, 2012, 101(22)： 223503.

[58] 刘少刚，程千驹，赵丹，等. 一种宽频压电能量收集装置的建模与实验研究[J]. 振动与冲击, 2016, 35(24)： 27-32.

LIU Shaogang,CHENG Qianju, ZHAO Dan, et al. Modeling and experiment of a piezoelectric energy harvester with wide operation bandwidth[J]. Journal of Vibration and Shock, 2016, 35(24)： 27-32.

[59] LIU H C, TAY C J, QUAN C G，et al. Piezoelectric MEMS energy harvester for low-frequency vibrations with wideband operation range and steadily increased output power[J]. Journal of Microelectromechanical Systems, 2011, 20(5)： 1131-1142.

[60] CHALLA V R, PRASAD M G, FISHER F T. A coupled piezoelectric-electromagnetic energy harvesting technique for achieving increased power output through damping matching[J]. Smart Materials and Structures, 2009, 18(9)： 095029.

[61] TADESSE Y, ZHANG S J, PRIYA S. Multimodal energy harvesting system: piezoelectric and electromagnetic[J]. Journal of Intelligent Material Systems and Structures, 2009, 20(5)： 625-632.

[62] KARAMI M A, INMAN D J. Equivalent damping and frequency change for linear and nonlinear hybrid vibrational energy harvesting systems[J]. Journal of Sound and Vibration, 2011, 330(23)： 5583-5597.

[63] MAHMOUDI S, KACEM N, BOUHADDI N. Enhancement of the performance of a hybrid nonlinear vibration energy harvester based on piezoelectric and electromagnetic transductions[J]. Smart Materials and Structures, 2014, 23(7)： 075024.

[64] SANG Y J, HUANG X L, LIU H X, et al. A vibration-based hybrid energy harvester for wireless sensor systems[J]. IEEE Transactions on Magnetics, 2012, 48(11)： 4495-4498.

[65] LI P, GAO S Q, NIU S H, et al. An analysis of the coupling effect for a hybrid piezoelectric and electromagnetic energy harvester[J]. Smart Materials and Structures, 2014, 23(6)： 065016.

[66] YU H, ZHOU J L, YI X Z, et al. A hybrid micro vibration energy harvester with power management circuit[J]. Microelectronic Engineering, 2015, 131： 36-42.

[67] SHAN X B, XU Z L, SONG R J, et al. A new mathematical model for a piezoelectric-electromagnetic hybrid energy harvester[J]. Ferroelectrics, 2013, 450(1)： 57-65.

[68] WANG H Y, TANG L H, GUO Y, et al. A 2DOF hybrid energy harvester based on combined piezoelectric and electromagnetic conversion mechanisms[J]. Journal of Zhejiang University-Science A, 2014, 15(9)： 711-722.

[69] XU Z L, SHAN X B, CHEN D P, et al. A novel tunable multi-frequency hybrid vibration energy harvester using piezoelectric and electromagnetic conversion mechanisms[J]. Applied Sciences, 2016, 6(1)： 10.

[70] UMEDA M, NAKAMURA K, UEHA S. Analysis of the transformation of mechanical impact energy to electric energy using piezoelectric vibrator[J]. Japanese Journal of Applied Physics, 1996, 35： 3267-3273.

[71] RASTEGAR J, PEREIRA C, NGUYEN H L. Piezoelectric-based power sources for harvesting energy from platforms with low-frequency vibration[C]∥ Proceedings of SPIE, San Diego, CA, 2006： 617101.

[72] GALCHEV T, AKTAKKA E E, NAJAFI K. A piezoelectric parametric frequency increased generator for harvesting low-frequency vibrations[J]. Journal of Microelectromechanical Systems, 2012, 21(6)： 1311-1320.

[73] WEI S, HU H, HE S Y. Modeling and experimental investigation of an impact-driven piezoelectric energy harvester from human motion[J]. Smart Materials and Structures, 2013, 22(10)：105020.

[74] LIU H C, LEE C K, KOBAYASHI T, et al. Investigation of a MEMS piezoelectric energy harvester system with a frequency-widened-bandwidth mechanism introduced by mechanical stoppers[J]. Smart Materials and Structures, 2012, 21(3)： 035005.

[75] 秦利锋，韩超然，杨磊，等. 一种基于碰撞的压电宽频能量收集装置[J]. 厦门大学学报(自然科学版)，2014，53(4)：502-507.

QIN Lifeng, HAN Chaoran, YANG Lei, et al. A broadband piezoelectric vibration energy harvester based on impact mechanism[J]. Journal of Xiamen University (Natural Science), 2014, 53(4)： 502-507.

[76] XU Z L, WANG W, XIE J, et al. An impact-based frequency up-converting hybrid vibration energy harvester for low frequency application[J]. Energies. 2017, 10(11)： 1761.

[77] WICKENHEISER A M, GARCIA E. Broadband vibration-based energy harvesting improvement through frequency up-conversion by magnetic excitation[J]. Smart Materials and Structures, 2010, 19(6)： 065020.

[78] TANG Q C, YANG Y L, LI X X. Bi-stable frequency up-conversion piezoelectric energy harvester driven by non-contact magnetic repulsion[J]. Smart Materials and Structures, 2011, 20(12)： 125011.

[79] PILLATSCH P, YEATMAN E M, HOLMES A S. A piezoelectric frequency up-converting energy harvester with rotating proof mass for human body applications[J]. Sensors and Actuators A-Physical, 2014, 206： 178-185.

[80] JUNG S M, YUN K S. Energy-harvesting device with mechanical frequency-up conversion mechanism for increased power efficiency and wideband operation[J]. Applied Physics Letters, 2010, 96(11)： 111906.

[81] HAN D, YUN K S. Piezoelectric energy harvester using mechanical frequency up conversion for operation at low-level accelerations and low-frequency vibration[J]. Microsystem Technologies, 2014, 21(8)： 1669-1676.

[82] REILLY E, MILLER L, FAIN R，et al. A study of ambient vibrations for piezoelectric energy conversion[C]∥ Proceedings of PowerMEMS, Washington, DC, 2009： 312-315.

[83] HARNE R L，WANG K W. A review of the recent research on vibration energy harvesting via bistable systems[J]. Smart Materials and Structures, 2013, 22(2)： 023001.

[84] PELLEGRINI S P, TOLOU N, SCHENK M，et al. Bistable vibration energy harvesters: a review[J]. Journal of Intelligent Material Systems and Structures, 2012, 24(11)： 1303-1313.