基于多目标拓扑优化的复合低屈服点钢阻尼器减震性能分析
2018-05-02何浩祥王小兵张小福
何浩祥, 王小兵, 张小福
(1. 北京工业大学 工程抗震与结构诊治北京市重点实验室,北京 100124; 2. 首都世界城市顺畅交通北京市协同创新中心,北京 100124)
在强震和强风作用下的建筑结构应具有足够的抗力和耗能能力才能够避免发生严重破坏。传统结构通过增强结构本身的抗震性能来抵御地震作用,即由结构本身储存和消耗地震能量,其自我调节能力较弱,导致结构和构件易出现损伤甚至倒塌。结构减震控制是在结构的特定部位布设耗能装置,以改变或调整结构的动力特性或动力作用,从而为结构抗震提供了一条安全有效的途径。当外部动力荷载或作用较大时,随着结构侧向变形的增大,耗能装置率先进入非弹性状态,产生较大阻尼,集中地耗散结构的地震或风振能量,从而避免或减小主体结构的振动反应和损伤。而耗能减震结构的实现主要依赖于简便实用的阻尼器。近年来,国内外研究者已研制出大量的阻尼器,如软钢阻尼器、摩擦阻尼器、黏滞流体阻尼器、智能阻尼器等,取得了丰硕的成果。
低屈服点金属阻尼器是各种耗能器中构造简单、滞回性能稳定、造价低廉、力学模型较明确的一种被动耗能装置,其利用金属不同形式的塑性滞回变形来消耗能量,在进入塑性状态后具有良好的滞回特性,因而被用来制造不同类型和构造形式的耗能阻尼器[1]。Kelly等[2]首次提出了安装金属耗能器耗能减震的概念并进行了相关的试验研究后,各国学者提出并研究出了各种形式的低屈服点金属阻尼器,如U形钢板阻尼器、锥形钢阻尼器、剪切屈服型钢阻尼器、轴向屈服型阻尼器等。日本Kajima公司提出了一种蜂窝状的金属屈服耗能器, 可安装在墙中或梁内。Whittaker等[3]和Tsai等[4]首先提出了X形和三角形的位移弯曲耗能型阻尼器;Tirca等[5]提出了一种平面内受力形式的钢阻尼器, 并对装有此种阻尼器的中高层结构进行了性能分析, 证明此阻尼器具有很好的耗能减震能力。周云等[6-7]先后开发了圆环耗能器、加劲圆环耗能器等多种金属耗能器;张文元等[8]提出了一种菱形开洞加劲阻尼器,其具有塑性变形大、滞回曲线饱满的优点,但初始刚度较小,钢材用量较大。为提高阻尼器的初始刚度,Mito等[9]提出了一种矩形剪切板阻尼器;李钢等[10]提出了单圆孔和双X型软钢阻尼器。该类阻尼器初始刚度较大,滞回曲线较饱满,但存在着应力集中现象,钢材利用率有待提高。虽然低屈服点金属阻尼器耗能减震技术的研究和应用已取得较大的进展,但还有许多问题有待研究和解决。①现有低屈服点钢板阻尼器大多属于封装结构,且外形单一、缺乏优化设计,不利于现场安装,维护成本较高;②由于阻尼器屈服强度仍然较高,在中小震下不能充分发挥材料滞回耗能的特性,为了最大程度发挥耗能体系的作用, 阻尼器应该同时具备低屈服点和屈服后具有良好变形耗能能力;③目前的阻尼器的屈服强度可调性比较差,需加强低屈服点钢板阻尼器用于已有建筑结构的抗震加固和修复方面的研究;④低屈服点阻尼器的可恢复性或可更换能力不足,需要适应可恢复功能结构的发展要求。因此开发成本低廉且具有较低屈服强度从而在地震中能够充分耗能的阻尼器具有重大的工程意义。鉴此,提出了复合型低屈服点钢板阻尼器,其屈服应力可根据工程需求进行调节,并将“最大刚度”和“满应力状态”同时作为优化目标实现阻尼器形状的拓扑优化,以使阻尼器具有更强的变形能力和耗能能力。在地震中,低屈服材料率先进入变形并达到屈服阶段,进行充分耗能减震,而主体结构不产生严重的塑性变形,保证整体抗震性能。主震后可迅速更换低屈服点组合钢板使节点整体抗震性能得到恢复,使钢结构节点和框架整体具备抵抗余震的能力。
1 复合低屈服点钢阻尼器构造及特性
1.1 低屈服点钢材料性能及试验
低屈服点阻尼器的用钢与传统钢结构用钢不同,其屈服强度低,在较小应变下即能出现塑性变形,并且具有足够的延展性和承载能力,且有良好的低周疲劳性能。因此,制作低屈服点钢阻尼器的关键技术之一是选取具有较低屈服强度和延伸率较大的金属耗能材料。常用的低屈服点金属包括软钢或低屈服点钢、铅、铝及锌铝合金等,其共同特点是塑性变形能力强、低周疲劳特性优越、滞回性能较稳定,并且可以回收利用。目前国内外关于利用低屈服点金属进行减震的理论研究较多,但能够达到工程应用的稳定性和安全性均较高的材料较少[11]。
选择国内最新研发的低屈服点钢LY160(屈服强度约为160 MPa)作为低屈服点耗能材料进行理论研究。为了获取并对比不同钢材的真实材料性能参数,选用Q345钢、Q235钢以及LY160钢三种材料进行对比分析。采用板状拉伸试件,根据相关试验标准[12]进行试件的加工。每种材质加工三个试件,在拉伸试验机上完成试件的准静态拉伸试验。拉伸速率为3 mm/min,在试件内放置纵向引伸计用来测量纵向应变,试件尺寸及拉伸后的破坏结果,如图1所示。将试验所得到的结果进行汇总分析,均值结果参见图2。可认为LY160钢具有预期的低屈服点以及优良的延展性和韧性,能够在较大变形下充分耗能,可以作为该复合型低屈服点阻尼器的材料。
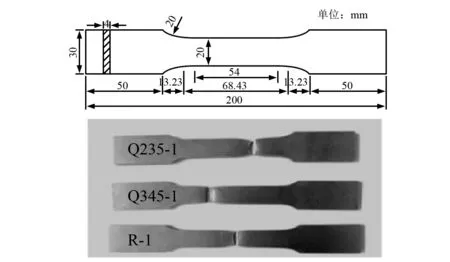
图1 试件尺寸和断裂形态 Fig.1 Specimen size and fracture morphology
1.2 复合低屈服点钢板阻尼器构造
根据以上材料性能,并针对传统低屈服点钢板阻尼器屈服点较高且不能调控的局限,本文提出新型的复合低屈服点钢板阻尼器。该阻尼器主要包括上下水平连接钢板和设置在上下水平连接板之间的局部镂空耗能金属板。耗能金属板由两种厚度一样的低屈服点钢(LY160)和普通钢(Q345)的钢板以不同比例组合,因此等效屈服强度较低且可调控。两种耗能金属板交错布置并相互之间固定连接,之后通过高强度螺栓连接,具体构造,如图3所示。耗能金属板的数量、尺寸和镂空形式应根据实际需求的屈服强度以及金属板之间的固定连接效果确定, 以确保具有足够的变形能力。复合低屈服点钢板阻尼器可结合支撑安装在结构梁下或填充墙内,在地震作用下,阻尼器先于结构进入塑性状态,实现充分耗能,从而确保主体结构的安全。
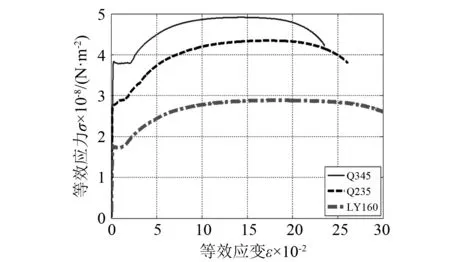
图2 不同钢材的应力应变曲线 Fig.2 Stress-strain curve of different steel
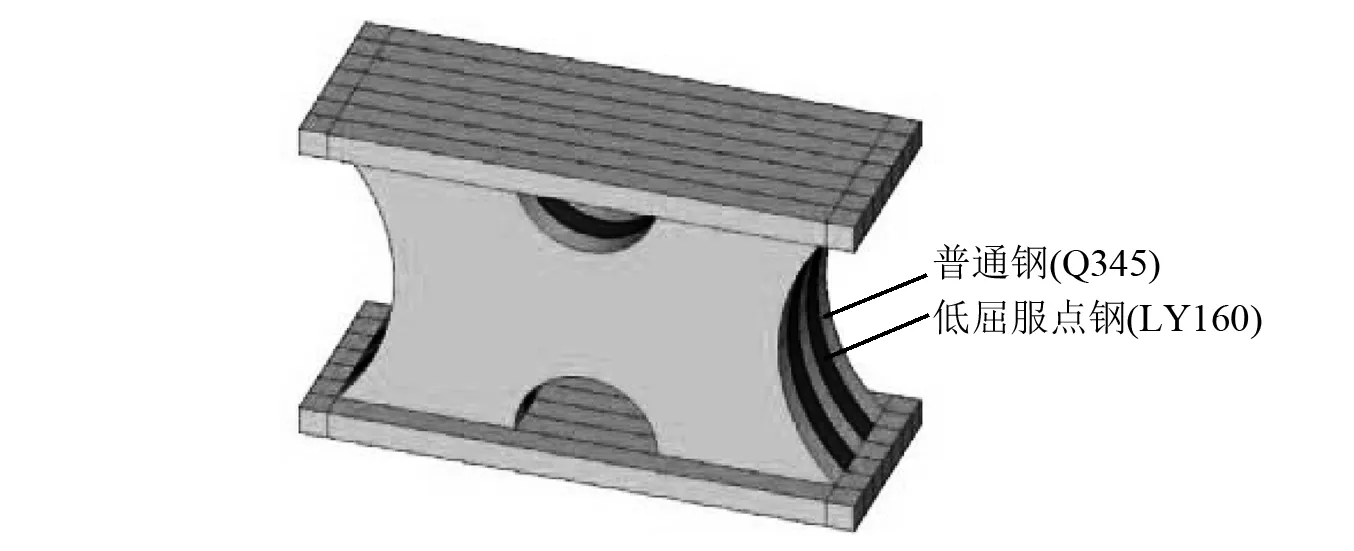
图3 复合低屈服点钢板阻尼器模型 Fig.3 Compound low yield point steel plate damper
与其它钢剪切阻尼器相比,本阻尼器的优点如下:①将具有不同屈服点的耗能金属板结合,与一般阻尼器相比,屈服强度降低,在中小震下即可充分发挥复合金属材料良好的滞回性能,使阻尼器能够获得较低的屈服应力和应变,同时又比单独采用LY160耗能金属板的阻尼器具有较好的延性和可控性;②可以根据实际抗震设计和维修要求,通过调整两种耗能金属板厚度比率以获得最佳屈服耗能效果,便于安装、升级和维修;③所用材料成本低廉,没有复杂构造,应用范围广泛。
2 基于满应力的阻尼器形状优化设计
2.1 阻尼器形状优化设计介绍
一般的低屈服点钢板阻尼器由矩形钢板或局部镂空的钢板叠加组成。矩形钢板通常只在中心有限区域内屈服,材料利用率偏低且阻尼器整体变形较小。局部开洞的镂空钢板沿高度方向在相同厚度处各点可能同时达到屈服,这将显著提高阻尼器的耗能能力和变形能力[13]。此外,部分低屈服点钢阻尼器采用钢板平面外受力方式,利用钢板弯曲屈服以后产生明显的塑性变形来达到耗能减震的目的,但此类阻尼器初始刚度较低、承载能力小。如果采用钢板在平面内剪切耗能的方案,则阻尼器具有较大的初始刚度,但这种受力方式易发生钢材应力集中破坏或局部屈曲现象,如果不针对镂空形式进行优化也很可能导致阻尼器的变形能力和耗能能力达不到预期要求。
针对上述问题,潘鹏等[14]对传统剪切型钢板阻尼器采用有限元数值模拟,得到了各种尺寸下的优化形状,如图4(a)所示。优化后的剪切型钢板阻尼器低周疲劳能力得到极大的提高,但耗散能力改进不明显。王强等[15]提出了一种新型钢板阻尼器,如图4(b)所示其在往复荷载作用下,初始刚度和屈服后刚度均较大,应力分布均匀且无明显应力集中现象,但易出现平面外屈曲。李钢等通过改变钢板平面几何形状提出了双X型钢阻尼器,如图4(c)所示。使其出现多点屈服,从而实现更好的耗能效果,但此类阻尼器存在屈服面积较小,钢材利用率不高等不足。

图4 镂空形式 Fig.4 The hollow form
上述钢板阻尼器存在不足的主要原因是其镂空形式主要依靠工程经验来确定,缺少更明确的优化目标和坚实的理论支持,这也导致相应的镂空形式并非最优。因此,有必要在结构拓扑优化设计理论的指导下对阻尼器的外部形状及镂空形式进行全面优化。
结构拓扑优化主要指对结构形式进行优化,其目标是在给定的设计域、约束条件及荷载下寻找结构的最佳材料分配方案。在传统的拓扑优化设计方法中,一般采用优化准则法作为求解方法,以体积为约束函数且将“最大刚度”作为优化目标,使结构在指定的体积约束下获得最大刚度。然而,在以“最大刚度”作为目标的优化一般只适合弹性分析,且对材料内部的应力状态考虑不充分。因此,如果采用上述拓扑优化方法得到的阻尼器形状优化方案的实际耗能能力未必是最优的,尚需结合其他优化目标进行综合优化[16-21]。
作为一种基本的结构优化设计方法,满应力设计可以使指定荷载下的结构绝大部分材料的应力均达到容许值,从而使材料被充分利用。满应力设计可解决一般弹塑性分析问题,其缺点是通常仅适用于静力荷载下静定结构的优化设计[22-23]。综上分析,如果将“最大刚度”和“满应力状态”同时作为优化目标,经过多次调整和修正,可以使结构在具有较大的刚度情况下充分发挥材料性能,达到刚度和满应力的最佳平衡,从而获得更全面的优化方案。因此,本文提出基于满应力的结构形状拓扑优化方法,并将之应用于低屈服点钢板阻尼器的形状优化中,力求使低屈服点钢板阻尼器具有最优的滞回性能和耗能能力。在一般的拓扑优化分析软件中,可交替将“最大刚度”和“满应力状态”作为优化目标,获得指定体积减小率下的双优化结果,再对比不同体积减小率下的优化结果确定最终的优化方案,具体优化流程,如图5所示。

图5 双目标拓扑优化设计流程 Fig.5 Optimization process
2.2 优化模型及结果
根据上述优化思想和设计流程,对复合低屈服点钢板形状进行优化。依据李钢等提出的双X模型, 考虑到其受剪能力的不足,本文提出内部优化阻尼器形式,如图6(a)所示。由于潘鹏等的单边优化模型,并没有使材料的利用率达到最大,故提出边缘优化阻尼器模型,如图6(b)所示。对王强等的模型改进而形成椭圆优化模型,弥补了其平面外易屈曲的不足,如图6(c) 所示。各模型的钢板长为35 cm,宽为20 cm,厚度为2 cm。现对图8中的三种阻尼器的初步形状进行进一步的优化设计。
首先,建立如图6(a)所示的阻尼器金属板的初步优化有限元模型,并将模型下端固定,在上端面施加水平荷载。其次,在指定体积减小率下对模型进行形状拓扑优化设计,绘制模型最终应力云图,如图7(a)所示。若最大应力分布均匀,则可认为模型已接近满应力状态,并确定现有模型为该体积减小率下的最终优化方案。否则,应适当削弱应力较小区域的体积并修改阻尼器模型,如图7(b)所示。并再次进行形状的拓扑优化,直至模型达到满应力状态,即为该体积减小率下的最优尺寸,如图7(c)所示。最后,综合考虑各种去除材料条件下的优化结果以及模型的整体效果,对比各体积减小率下的最优尺寸,确定最终的优化方案,内部优化模型阻尼器的形式,如图7(d)所示。
星雨说:“我小时候,每年四月,祖姑婆会用她的小马车带我去洛阳城里小住一段时间,品新茶,看牡丹。姚黄魏紫其实没什么好看,我特别喜欢去洛阳的旅行。由风凌渡过黄河,华山的险峰像一朵朵巨大的莲花开放在远处的原野边上,泾水渭河在更远的地方蜿蜒缓流,嵩山间曲折的山路,路边的松树春天里发出的气味真好闻。在龙门看那些石窟中面目慈悲的佛像,在少林寺山门外看和尚们练拳,一路上霜雪销尽,阳光照着树木发出新芽,翠翠的,路边是不知名的野花,布谷和杜鹃在山林深处啼叫,野猪与鹿被惊吓得乱跑,有时候拉着马车的两匹马都会停下来,吸着山谷里爽利的空气,听成百上千的鸟合唱。”
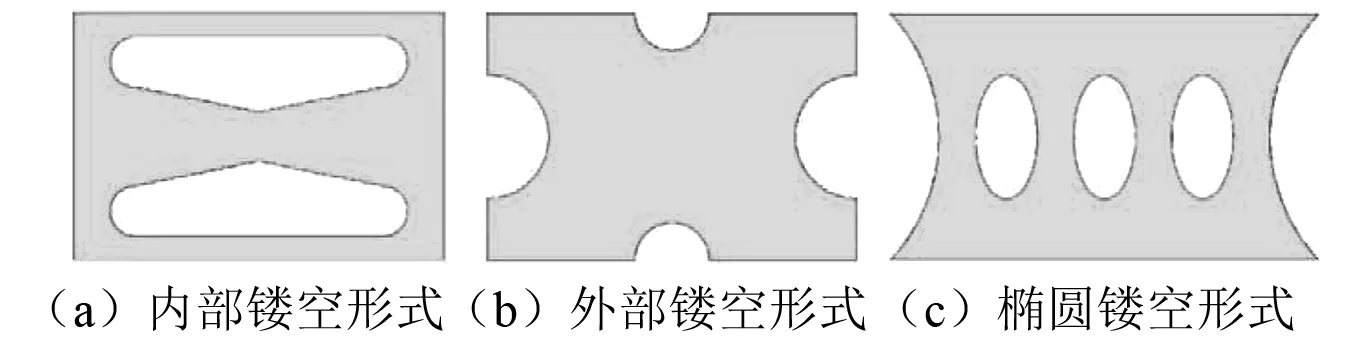
图6 阻尼器初步形式 Fig.6 The initial form of damper
按照图5及上述内部优化模型阻尼器的过程,同样可得到边缘优化模型的最终方案,如图8所示。此外,椭圆优化模型的结果,如图9所示。各阻尼器优化后的最终尺寸,如图10所示。确定了阻尼器的最优形式后,尚需进行更深入的弹塑性分析,进一步验证优化阻尼器的耗能性能。

图7 内部优化模型优化过程 Fig.7 Optimization process of internal optimization model

图8 边缘优化模型过程 Fig.8 Optimization process of edge optimization model

图9 椭圆优化模型过程 Fig.9 Optimization process of ellipse optimization model

图10 各阻尼器优化后的尺寸(mm) Fig.10 Optimized size (mm)
3 模拟分析及验证
3.1 不同形状阻尼器性能对比
对阻尼器进行拓扑优化后,为了验证相应的复合型低屈服点钢板阻尼器的性能,建立了阻尼器有限元模型,如图3所示。其中第一种耗能金属为Q345钢,第二种耗能金属LY160钢。将模型的上端面固定,在下端面施加低周往复荷载。三种模型的整体滞回曲线,如图11所示。采用Q345钢和LY160钢的钢板应力云图,如图12和图13所示。
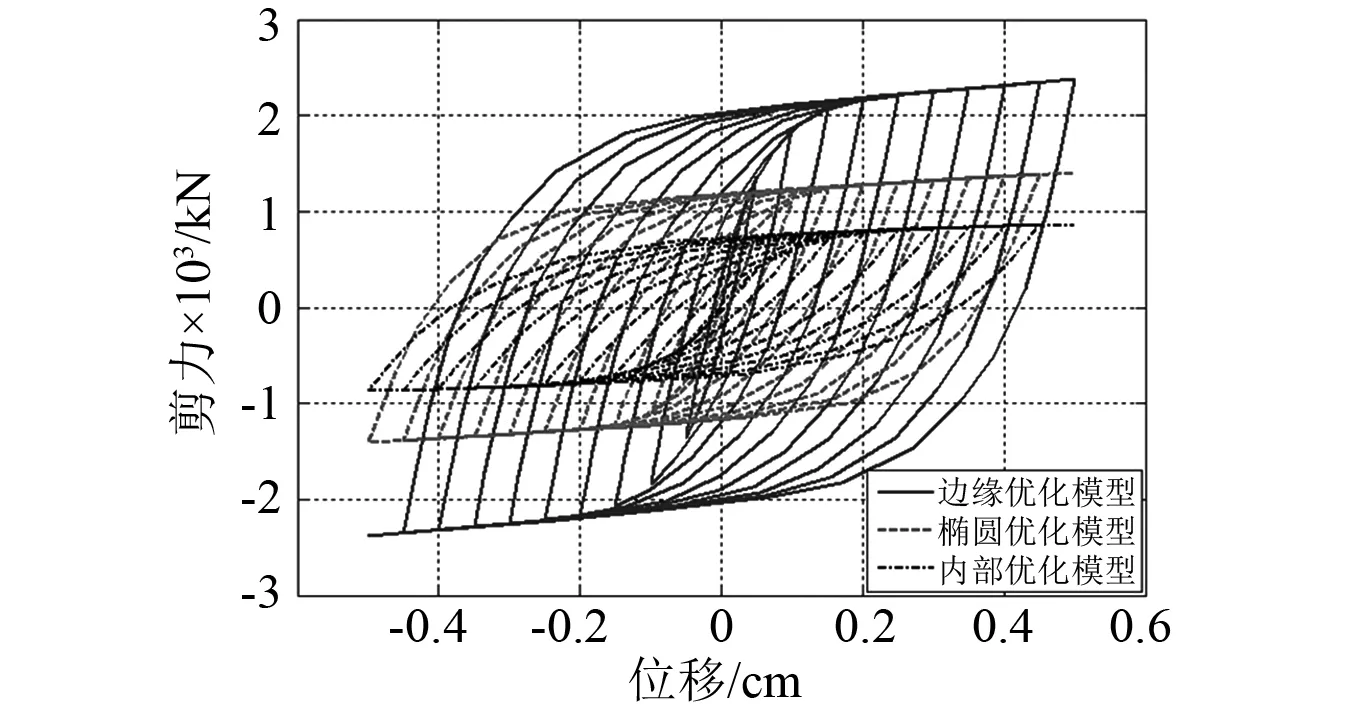
图11 三种模型滞回曲线对比 Fig.11 Comparison of hysteresis curves
由各滞回曲线计算结果可以看出:在同样的位移加载下,内部优化阻尼器的屈服力较小,
具有较强的变
形能力。边缘优化阻尼器在平面内受力时表现出良好的塑性性能,滞回曲线饱满,塑性变形较大,同时具有较大的初始刚度和优越的耗能能力。由各阻尼器的应力云图可以看出:内部优化阻尼器应力分布较均匀,但应力水平相对较低。边缘优化阻尼器受力均匀,应力水平高,最符合满应力设计准则。椭圆优化模型的应力集中现象较明显,耗能利用率偏低。
此外,由图11可知,在同样力下,边缘优化模型阻尼器的位移较小,且其初始刚度明显大于其他两个阻尼器。可见,边缘优化模型钢板阻尼器能够有效的提高节点的承载能力和初始刚度,具有更加优良的抗震能力。
综上分析,可认为内部优化阻尼器适用于需要大变形阻尼器的减震结构;边缘优化阻尼器耗能能力强,综合性能最优,而椭圆优化阻尼器可能出现由应力集中导致装置失效的情况,不推荐使用。
为了更直观地比较不同类型阻尼器的耗能能力,选用等效滞回阻尼比计算模型来分别考虑不同阻尼器在低周往复荷载下的性能[24-25]。
(1)
式中:ED为结构单周期运动滞回阻尼耗能,等于滞回环包围的面积;ES为最大应变能。

图12 各阻尼器Q345钢板应力云图 Fig.12 Stress nephogram of Q345 steel plate for each damper

图13 各阻尼器LY160钢板应力云图 Fig.13 Stress nephogram of LY160 steel plate for each damper
计算各阻尼器在不同位移下的等效滞回阻尼比曲线,如图14所示。由图14可知,在加载初期各阻尼器的耗能能力较接近,随着变形的变大,耗能能力均不断变大,一直保持稳定上升。在加载后期,边缘优化模型和椭圆优化模型的等效阻尼比增长更快,说明其耗能能力在快速提升,而内部优化模型的耗能能力略低。
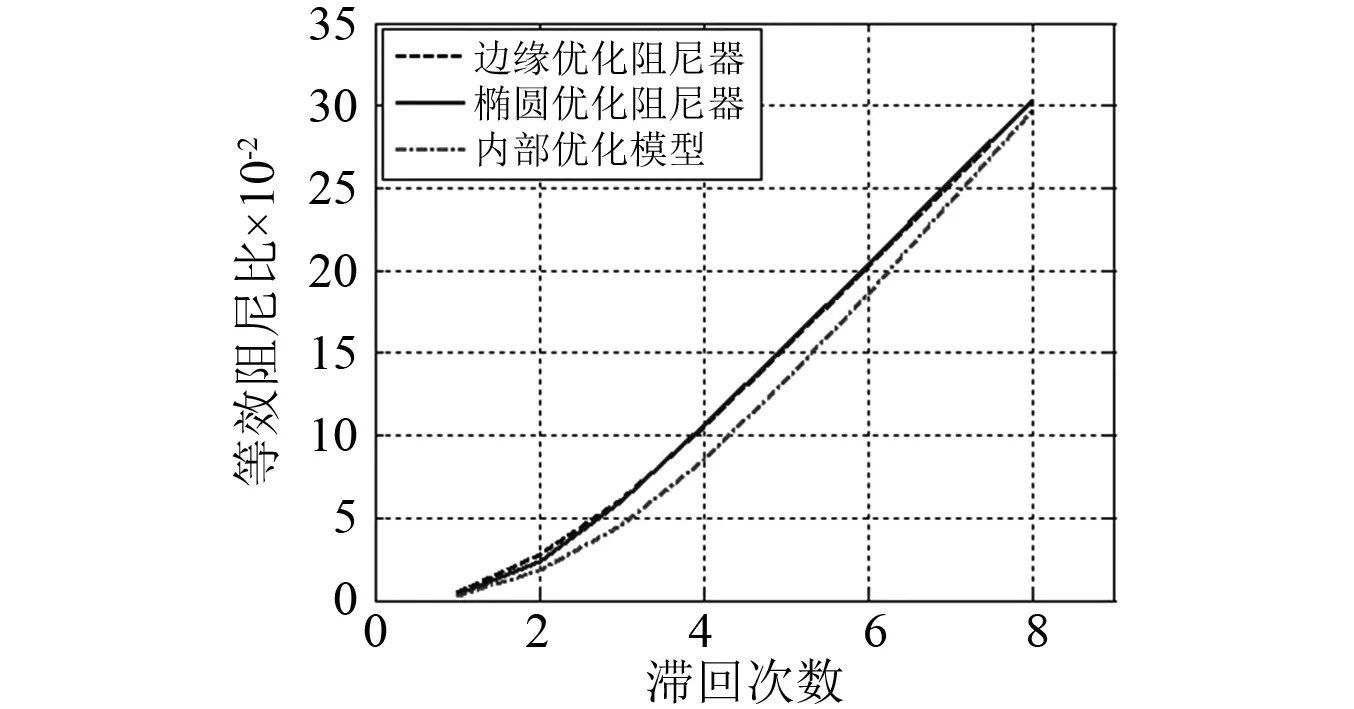
图14 不同阻尼器的等效阻尼比对比 Fig.14 Comparison of equivalent damping ratio
3.2 同一阻尼器不同材料配比性能对比
为了验证阻尼器的可调性,需研究不同材料配比对阻尼器性能的影响。现选用前述三种方案研究复合阻尼器的性能,具体参数见图10。各方案均采用5块厚度为2 cm的钢板,但钢板的材料性能和组合比例不同。其中:方案一的5块钢板全部采用LY160;方案二的5块钢板全部采用Q345;方案三为3块Q345和2块LY160相互叠合。对阻尼器进行低周往复加载分析。图15和图16分别为三种方案下不同阻尼器滞回曲线。由滞回曲线对比图可以知,采用方案三的阻尼器的屈服强度介于方案一和方案二的结果之间,因此通过改变Q345和LY160的组合比例,能够按预期调整阻尼器屈服强度。

图15 内部优化模型阻尼器滞回曲线 Fig.15 Hysteresis curves of internal optimization model damper
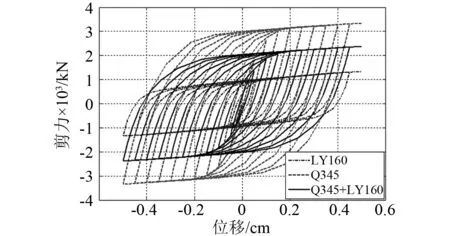
图16 边缘优化模型阻尼器滞回曲线 Fig.16 Hysteresis curves of edge optimization model damper
4 复合低屈服点钢阻尼器在结构中的应用
采用内部优化模型和边缘优化模型阻尼器的钢结构整体耗能减震性能还有待进一步对比。采用ANSYS建立单层结构整体模型。该框架高1.5 m,跨度为3.0 m,柱截面尺寸为200 mm×200 mm,梁截面尺寸为200 mm×180 mm,斜支撑板尺寸为100 mm×200 mm。为简化计算过程,梁、柱和阻尼器均采用实体单元,斜支撑采用梁单元。将底层柱子与地面刚性固结,在柱端施加往复位移荷载。阻尼器在框架中的模型及阻尼器与梁连接的节点模型,如图17所示。

图17 阻尼器框架模型 Fig.17 Damper model in the frame
提取阻尼器的位移和剪力时程曲线,如图18和图19所示。由图18和图19可知,装有边缘优化阻尼器的框架剪力明显大于装有内部优化阻尼器和纯框架下的剪力,表明边缘优化阻尼器具有更优越的耗能能力并能明显提高结构抗力。
框架中阻尼器的应变云图及荷载位移曲线,如图20和图21所示,由图20和图21可知,边缘优化模型阻尼器的云图颜色均匀,其滞回曲线更饱满,耗能效果明显。阻尼器各滞回环下的耗能对比,如图22所示。也表明边缘优化阻尼器的耗能能力更加突出。

图18 框架中阻尼器位移时程对比 Fig.18 Comparison of displacement time-history in frame

图19 整体框架力时程对比 Fig.19 Comparison of force time-history
综上可认为,本文提出的边缘优化阻尼器比内部优化阻尼器具有更优越的耗能减震能力,在实际应用中推荐优先使用边缘优化复合低屈服点钢板阻尼器。
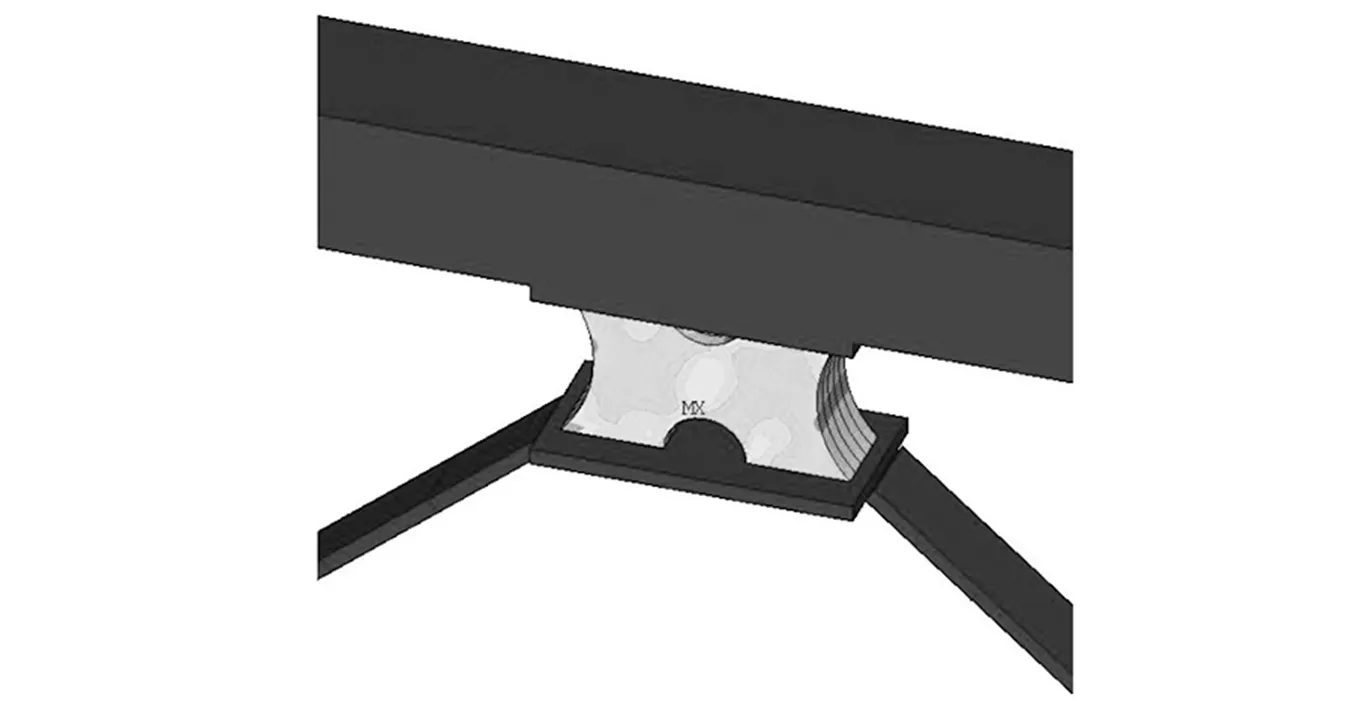
图20 边缘优化模型阻尼器在框架中的应变云图 Fig.20 Strain nephogram of edge optimization model damper
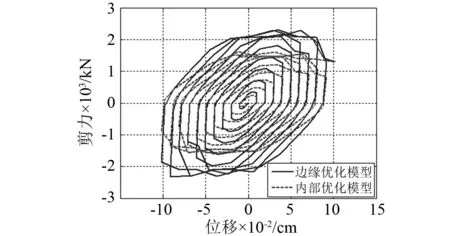
图21 框架中阻尼器的滞回曲线 Fig.21 Hysteretic curves of damper in frame

图22 阻尼器耗能对比 Fig.22 Comparison of energy dissipation
进一步研究地震动下两种阻尼器对钢结构减震性能影响。由于利用ANSYS进行结构地震动非线性时程分析的计算效率偏低,本文采用Etabs进行时程分析。通过Etabs建立与ANSYS中有限元模型相同的一层框架并在模型的支撑节点采用阻尼器单元,通过设置连接单元的属性参数,使其在低周往复加载下的滞回曲线与ANSYS中的相关结果接近,如图23所示。连接单元的属性类型为“阻尼器”,相关出力为F=Cva,其中C为阻尼,y为位移,a为阻尼指数。

图23 ANSYS和Etabs中滞回曲线对比 Fig.23 Comparison of hysteresis curves
其中,模拟边缘优化模型阻尼器的阻尼指数a为2,阻尼为3 000 kN·s/m,内部优化模型阻尼器的阻尼指数a为1.85,阻尼为3 500 kN·s/m。
为了进一步研究多层结构的减震性能,利用Etabs软件分别建立安装有边缘优化模型阻尼器和内部优化模型阻尼器的单榀三层钢框架模型以及仅安装普通支撑的钢框架模型,如图24所示。钢框架层高均为3.6 m,跨度为6.0 m。框架柱截面为H4000×3000×25×25(mm),梁截面尺寸为H250×150×20×12(mm)。斜支撑截面尺寸为H150×150×12×8(mm)。用图23连接单元属性的参数模拟阻尼器,材料均采用Q345钢,所在场地类型为Ⅱ类,抗震设防烈度为8度。
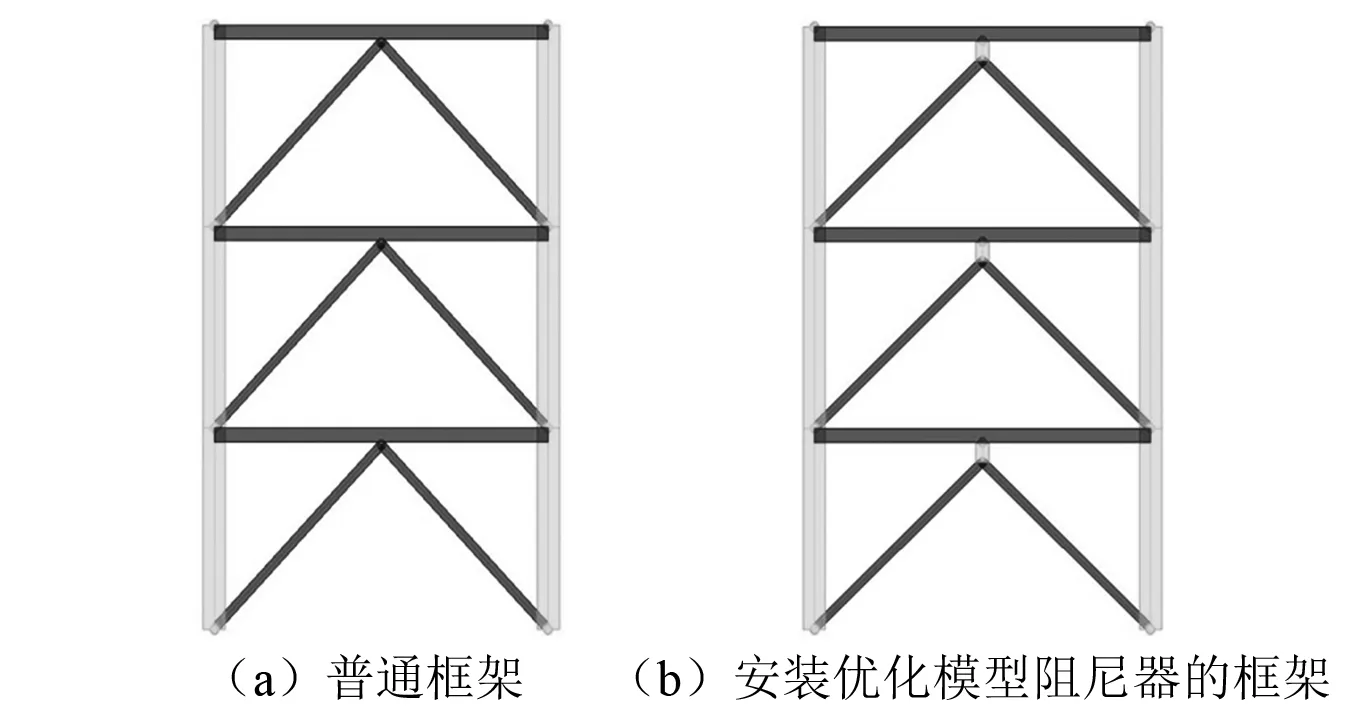
图24 有控结构与无控结构的框架平面图 Fig.24 Plane graph of uncontrolled frame and controlled frame
为研究和对比以上三种结构的减震性能,根据场地条件选取El Centro波、Taft波和OCTT波进行动力时程分析。为了考虑地震动幅值对损伤程度的影响,依据抗震设计规范要求将每一组地震动X向的加速度幅值分别调至0.70 m/s2、1.96 m/s2和4.00 m/s2,从而分别作为小震、中震和大震下的地震动输入。
提取小震、中震和大震下各结构的顶层绝对位移和顶层绝对加速度。其中,峰值减震率指减震后与减震前的结构响应最大值的差值与减震前结构响应最大值的比值;能量减震率指无控与有控的响应包络面积差与无控响应包络面积的比值。其中A表示装有边缘优化模型阻尼器的结果,B表示装有边缘优化模型阻尼器的结果。具体结果,如表1所示。
图25和图26分别为El Centro波小震和大震下的
结构顶层位移时程曲线。由表1和图25和图26可知,边缘优化模型阻尼器和内部优化模型阻尼器对结构减震效果均较明显,且前者减震能力更强。此外,随着地震动幅值增大,阻尼器的弹塑性耗能能力逐渐得到充分发挥,减震效果也越明显。综上所述,低屈服点金属阻尼器具有良好而稳定的减震性能,可明显改善结构的抗震能力,在实际工程应用中推荐优先使用边缘优化复合低屈服点阻尼器。
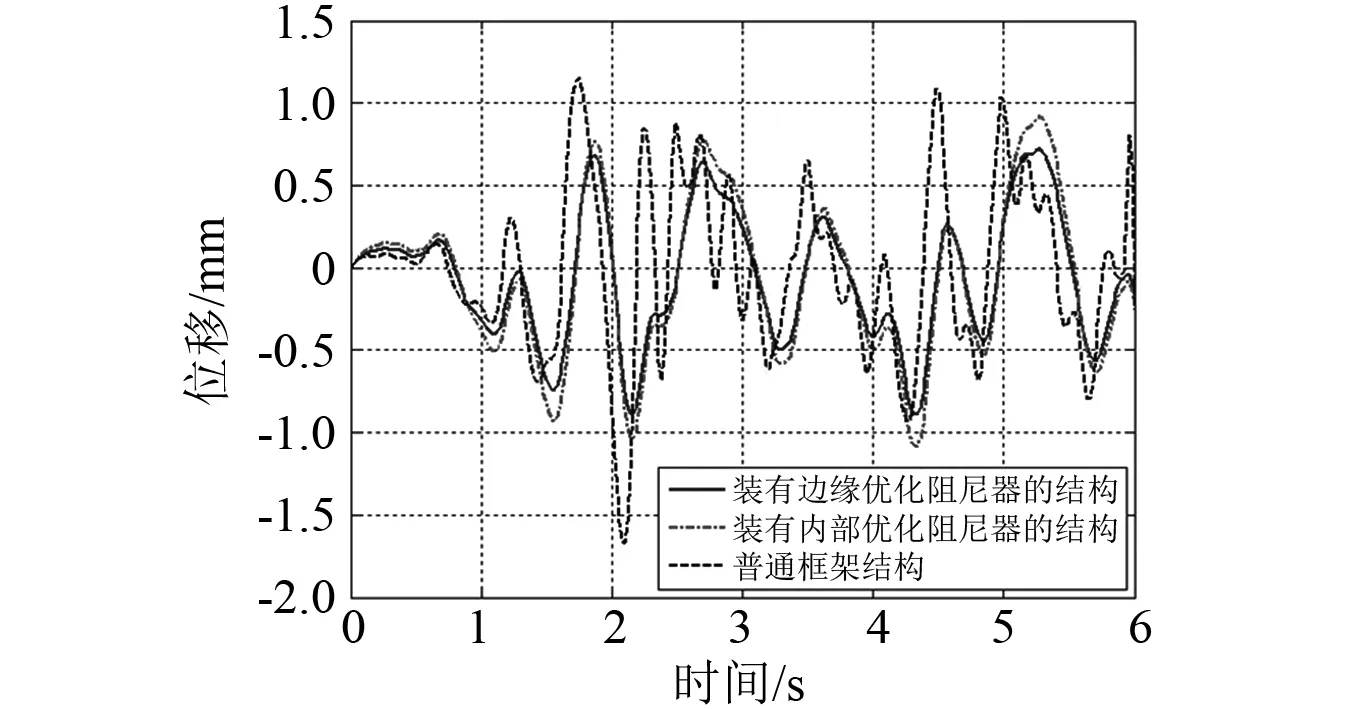
图25 小震下框架位移时程曲线 Fig. 25 Time history curve under small earthquake

图26 大震下框架位移时程曲线 Fig.26 Time history curve under large earthquake
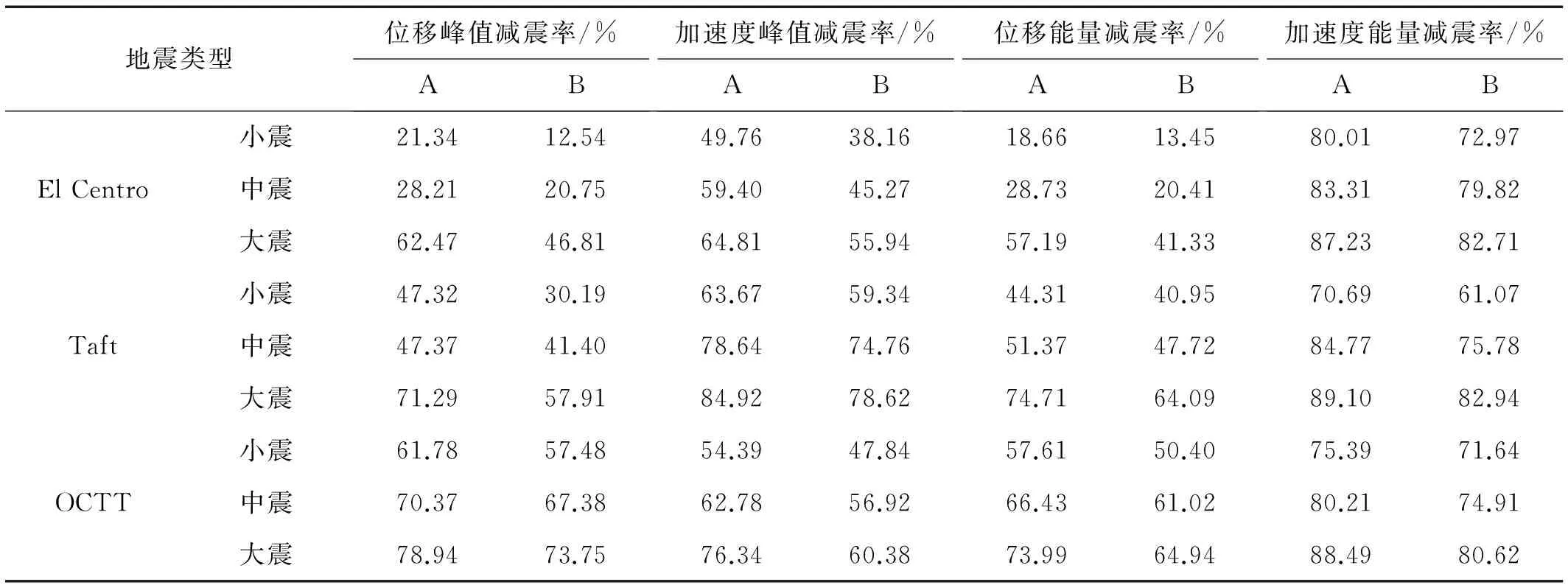
地震类型位移峰值减震率/%AB加速度峰值减震率/%AB位移能量减震率/%AB加速度能量减震率/%AB小震21.3412.5449.7638.1618.6613.4580.0172.97ElCentro中震28.2120.7559.4045.2728.7320.4183.3179.82大震62.4746.8164.8155.9457.1941.3387.2382.71小震47.3230.1963.6759.3444.3140.9570.6961.07Taft中震47.3741.4078.6474.7651.3747.7284.7775.78大震71.2957.9184.9278.6274.7164.0989.1082.94小震61.7857.4854.3947.8457.6150.4075.3971.64OCTT中震70.3767.3862.7856.9266.4361.0280.2174.91大震78.9473.7576.3460.3873.9964.9488.4980.62
5 结 论
针对传统低屈服点钢板阻尼器屈服点较高且不能调控的局限,提出了三种复合型低屈服点钢板阻尼器,耗能金属板由低屈服点钢和普通钢钢板以不同比例组合。基于“最大刚度”和“满应力状态”的理念,通过交替优化的方法对边缘镂空、内部镂空和椭圆镂空等三种钢板阻尼器的新型镂空形式进行拓扑优化,得到三种同时满足最大刚度和满应力状态优化目标的复合低屈服点钢板阻尼器形状。
对优化后的复合型钢板阻尼器进行有限元模拟分析,结果表明内部优化阻尼器适用于需要大变形阻尼器的减震结构;边缘优化阻尼器耗能能力强,综合性能最优。对不同材料配比的内部优化阻尼器和边缘优化阻尼器进行了研究,证明其能够按预期调整该复合型阻尼器的屈服点。
为了验证结构的实际减震效果,对装有不同类型阻尼器的钢框架结构进行仿真分析。结果表明本文提出的边缘优化阻尼器比内部优化阻尼器具有更优越的耗能减震能力,在实际工程应用中推荐优先使用边缘优化复合低屈服点钢板阻尼器。
[ 1 ] 章丛俊,李爱群,赵明. 软钢阻尼器耗能减震结构的研究与应用综述 [J]. 工业建筑,2006,36(9): 17-21
ZHANG Congjun, LI Aiqun, ZHAO Ming. Summary of research on and applications of passive energy dissipation systems of mild steel damper [J]. Industrial Construction, 2006, 36(9): 17-21.
[ 2 ] KELLY J M, SKINNER R I, HEINE A J. Mechanisms of energy absorption in special devices for use in earthquake-resistant Structures [J]. National Society for Earthquake Engineering,1972, 5(3): 63-88.
[ 3 ] WHITTAKER A S, BERTERO V V, THOMPSON C I, et al. Sesismic testing of steel plate energy dissipation devices [J]. Earthquake Spectra, 1991, 7(4): 563-604.
[ 4 ] TSAIK K C, CHEN H W, HONG C P, et al. Design of steel triangular plate energy absorbers for seismic resistant construction [J]. Earthquake Spectra, 1993,9(3): 505-528.
[ 5 ] TIRCA L D, FOTI D, DIAFERIO M. Response of middle rise steel frames with and without passive dampers to near field ground motions[J], Engineering Structures,2003,25(2):169-179.
[ 6 ] 周云,刘季. 圆环耗能器的试验研究[J]. 世界地震工程,1996,11(4): 1-7.
ZHOU Yun, LIU Ji. Experimental study on the behavior of circular ring energy dissipator [J]. World Information on Earthquake Engineering, 1996, 11(4): 1-7.
[ 7 ] 周云,刘季. 新型耗能(阻尼)减震器的开发与研究[J]. 地震工程与工程振动,1998,18(1): 71-79.
ZHOU Yun, LIU Ji. Development and study of new energy dissipaters (dampers) [J]. Earthquake Engineering and Engineering Vibration, 1998,18(1): 71-79.
[ 8 ] 张文元,张敏政,李东伟. 新型加劲软钢阻尼器性能与试验[J]. 哈尔滨工业大学学报,2008,40(12): 1888-1894.
ZHANG Wenyuan, ZHANG Minzheng, LI Dongwei. An experimental research on performance and application of a new type of mild steel damper added damping and stiffness (ADAS) [J]. Journal of Harbin Institute of Technology, 2008, 40(12): 1888-1894.
[ 9 ] MITO M, TAMURA R, SHIMIZU K, et al. Study on seismic design method for building with steel damper (Part1)[C]∥Proceedings of AIJ Annual Meeting, 1997.
[10] 李钢, 李宏男. 新型软钢阻尼器的减震性能研究[J]. 振动与冲击,2006,25(3):66-72.
LI Gang, LI Hongnan. Study on vibration reduction of structure with a new type of mild metallic dampers [J]. Journal of Vibration and Shock, 2006, 25(3): 66-72.
[11] 田洁, 颜智超, 卢俊龙. 极低屈服点钢在密肋壁板结构中的减震控制研究[J].振动与冲击, 2014, 33(5): 160-164.
TIAN Jie, YAN Zhichao, LU Junlong. Aseismic control of a multi-ribbed slab structure using ultra low yield strength steel [J]. Journal of Vibration and Shock, 2014, 33(5): 160-164 .
[12] 金属材料拉伸试验第1部分: 室温试验方法:GB/T 228.1—2010 [S]. 北京:中国标准出版社, 2011.
[13] 邢书涛,郭迅. 一种新型软钢阻尼器力学性能和减震效果的研究 [J].地震工程与工程振动, 2003,23(6): 179-186.
XING Shutao, GUO Xun. Study on mechanical behavior and effectiveness of a new type of mild steel damper [J]. Earthquake Engineering and Engineering Vibration, 2003, 23(6): 179-186.
[14] DENG Kailai, PAN Peng, SUN Jiangbo, et al. Shape optimization design of steel shear panel dampers [J]. Journal of Constructional Steel Research,2014, 99: 187-193.
[15] 王强, 安立刚,刘明,等. 新型钢板阻尼器的减震性能分析[J]. 土木工程学报, 2010, 43: 341-344.
WANG Qiang, AN Ligang, LIU Ming, et al. Analysis on vibration suppression of a new type of planar steel damper [J]. China Civil Engineering Journal, 2010, 43: 341-344.
[16] LIU Y,SHIMODA M. Shape optimization of shear panel damper for improving the deformation ability under cyclic loading [J]. Structural & Multidisciplinary Optimization, 2013, 48(2): 427-435.
[17] OHSAKI M. Optimization of finite dimensional structures [M]. CRC Press; 2010.
[18] PAN P, OHSAKI M, TAGAWA H. Shape optimization of H-beam flange for maximum plastic energy dissipation [J]. Journal of Structural Engineering, 2015, 133(8): 1176-1179.
[19] VANDERPLAATS G N. Multidiscipline design optimization [J]. Applied Mechanics Reviews, 1988, 41(6): 257-262.
[20] KIRSCH U, BOGOMOLNI M, SHEINMAN I. Efficient procedures for repeated calculations of the structural response using combined approximations [J]. Computers & Structures, 2000,78 (Sup1/Sup2/Sup3): 449-457.
[21] 谢亿民,黄晓东. 渐进结构优化法(ESO) 和双向渐进结构优化法(BESO) 的近期发展[J].力学进展,2011,41(4): 462-471.
XIE Yiming, HUANG Xiaodong. Recent developments of evolutionary structural optimazation (ESO) and bidirectional evolutionary structural optimization(BESO)[J]. Advances in Mechanics, 2011, 41(4): 462-471.
[22] LIU Q M. A design method of rib distribution for thin plate structure based on the full stress rule [J]. Machinery Design & Manufacture, 2007, 1(1):23-24.
[23] 丁晓红,程莉. 基于SKO 方法的满应力结构拓扑优化设计[J]. 中国机械工程, 2009, 20(15): 1765-1770.
DING Xiaohong, CHENG Li. Topology optimization of full-stressed structures based on SKO method [J]. China Mechanical Engineering, 2009, 20(15): 1765-1770.
[24] NEHRP commentary on the guidelines for the seismic rehabilitation of buildings:FEMA274[S].Washington DC: Federal Emergency Management Agency, 1997.
[25] Seismic evaluation and retrofit of concrete buildings [R]. ATC Redwood City, California, USA, 1996.
