部分柱顶滑移钢筋混凝土框剪结构的地震扭转反应分析

吕文龙， 吴 波

(1. 华南理工大学 亚热带建筑科学国家重点实验室，广州 510640； 2. 广东省建筑科学研究院集团股份有限公司，广州 510500)

强震作用下建筑物常常出现落层倒塌。所谓落层倒塌是指结构某层(或该层绝大部分)突然整体下挫，该层楼盖与下层楼盖发生大面积接触碰撞的一类倒塌破坏现象。若结构相邻几层从上到下依次发生连续性的落层倒塌破坏，则称其为连续落层倒塌。2008年我国汶川地震以及1995年日本阪神地震中，不少建筑物都发生了底部或中部薄弱楼层损毁的落层倒塌现象[1-2]。虽然落层破坏是建筑物倒塌的一类典型模式，国内外学者对与之相关的薄弱层形成机理也有一定认识[3-5]，但世界范围内有关其防控对策方面的研究还相对很少[6]。显然，这给建筑物落层破坏(特别是连续落层破坏)的发生埋下了隐患。文献[7]提出了抗落层倒塌部分柱顶滑移钢筋混凝土框架结构的基本思想。文献[8-12]将该思想拓展到超高层建筑的常用结构形式——框剪结构，介绍了部分柱顶滑移钢筋混凝土框剪结构的设想，对比了该新型结构与传统框剪结构的设计过程，比较了二者的经济性及弹塑性地震响应，给出了滑移柱柱顶摩擦因数的估算方法及P-δ效应的计算方法，进行了振动台试验研究，试验结果表明该新型结构具有比传统框剪结构更优的抗震性能。

对于部分柱顶滑移钢筋混凝土框剪结构，部分柱顶设置摩擦支座后，小震情况下摩擦支座尚未起滑，由吴波等的研究可知摩擦支座会在一定程度上削弱滑移柱的抗侧刚度，虽然滑移柱的截面尺寸比相同条件下设计的常规框剪结构的框剪柱有所增大，但也有可能不足以抵消摩擦支座所引发的抗侧刚度减小效应，从而导致结构的抗扭刚度比相同条件下设计的常规框剪结构有所削弱；大震情况下摩擦支座滑动，结构的抗扭刚度比相同条件下设计的常规框剪结构也可能有所削弱。因此，地震作用下此类结构的扭转效应很可能与常规框剪结构有所不同，有必要对其进行专门研究。本文主要研究偶然偏心对部分柱顶滑移框剪结构地震扭转效应的影响。

1 部分柱顶滑移钢筋混凝土框剪结构

部分柱顶滑移框剪结构的某些框架柱在其柱顶部位与相邻节点断开，并在二者之间设置摩擦支座。当摩擦支座的摩擦因数较小时，这部分框架柱(即滑移柱)将主要承受上部结构传来的轴力而较少承受弯矩和剪力，强震作用下它们可基本保持完好。若它们在设计之初就被赋予有单独承担绝大部分结构自重的能力，则可较好地确保结构的抗倒塌能力。

滑移柱柱顶与相邻节点之间的摩擦支座由上摩擦板和下摩擦板组成(图1(a))。小震作用下，为充分利用滑移柱的抗侧刚度，一般希望摩擦支座不起滑，此时该支座可传递剪力和少量弯矩。作为近似处理，对于小震阶段的摩擦支座，可采用普通铰进行模拟[8]，即滑移柱的上、下边界条件分别为铰接和刚接(图1(b))。

大震作用下摩擦支座已经起滑，故采用图1(c)所示摩擦单元进行模拟[13-14]。每个摩擦单元由两个节点组成：节点1位于下摩擦板中心位置，与柱单元共用节点；节点2位于节点核心区中心位置，与梁单元共用节点。摩擦单元也可用于小震计算，但计算过程比普通铰繁琐。

图1 滑移柱柱顶与相邻节点的连接及其力学模型 Fig.1 Realization and mechanical models of connection between sliding column’s upper end & adjacent joint

对于上、下摩擦板之间的摩擦接触，考虑如下摩擦力-变形关系：

Fax=μNZax,Fay=μNZay

(1)

式中：Fax和Fay分别为x方向和y方向的水平摩擦力；N为竖向压力；μ为滑动摩擦因数(具体取值详见后文第2.2节)；Zax和Zay为考虑摩擦支座运动状态、摩擦力方向及双向耦合效应的滞变分量，满足如下微分方程组[15]

(2)

式中：Y为滑动前摩擦支座的弹性剪切变形；ux和uy分别为上、下摩擦板沿x方向和y方向的相对位移；A，γ和β为控制摩擦力-变形滞回曲线整体形状的参数，本文取A=1、γ=0.9和β=0.1。

弹性剪切变形Y与滑动前摩擦支座的水平剪切刚度kx和ky之间具有如下关系：

Y=μN/kx=μN/ky

(3)

式中：kx=ky=560 kN/mm。

2 偶然偏心导致的弹性扭转反应

2.1 计算工况

采用通用软件Perform-3D进行本文的计算。计算过程中楼板刚度假定为无限大，且结构各层质量均集中于相应楼层的质心处。通过计算分析，着重考察如下三类影响：①各层质心在一定范围内的随机偏心对结构扭转反应的影响；②第一扭转周期与第一侧向周期之比对结构扭转反应的影响；③平面长宽比对结构扭转反应的影响。具体计算工况见表1，表中l为垂直地震作用方向的结构边长，b为平行地震作用方向的结构边长。

2.2 质心位置的影响

采用吴波等所提方法，设计一个10层的部分柱顶滑移框剪结构(结构一)，其平面布置见图2，各层层高均为3.3 m。梁、柱、墙的混凝土强度等级均为C30，梁纵筋采用HRB400，柱纵筋采用HRB335，墙分布钢筋及其边缘构件纵筋均采用HRB335。每层楼面荷载代表值10 kN/m2，抗震设防烈度7度，Ⅱ类场地。设计结果如下：

表1 计算工况Tab.1 Calculation cases

框架梁截面250 mm×500 mm，剪力墙截面200 mm×2 000 mm，滑移柱截面1～5层700 mm×700 mm/6～10层600 mm×600 mm，常规柱截面1～5层600 mm×600 mm/6～10层500 mm×500 mm。1～5层剪力墙的横向和竖向配筋率分别为0.5%和0.25%，其边缘构件的截面200 mm× 500 mm/纵筋配筋率1.2%/体积配箍率1.6%(箍筋采用HRB335)；6～10层剪力墙的横向和竖向配筋率均为0.25%，其边缘构件的截面200 mm×500 mm/纵筋配筋率0.9%/体积配箍率0.8%(箍筋采用HRB335)。各层常规柱的纵筋配筋率均为0.8%，1～5层、6～10层常规柱加密区体积配箍率分别为1.2%(箍筋采用HRB335)、1.4%(箍筋均采用HPB235)；各层滑移柱的纵筋配筋率也均为0.8%。框架梁的顶面纵筋配筋率1.5%，底面纵筋配筋率1.2%，加密区体积配箍率0.7%(箍筋采用HPB235)。各层摩擦支座的摩擦因数分别为1～3层0.02、4～6层0.03、7层0.04、8层0.05、9层0.07、10层0.12，各层。结构一各层刚心与平面几何中心重合。

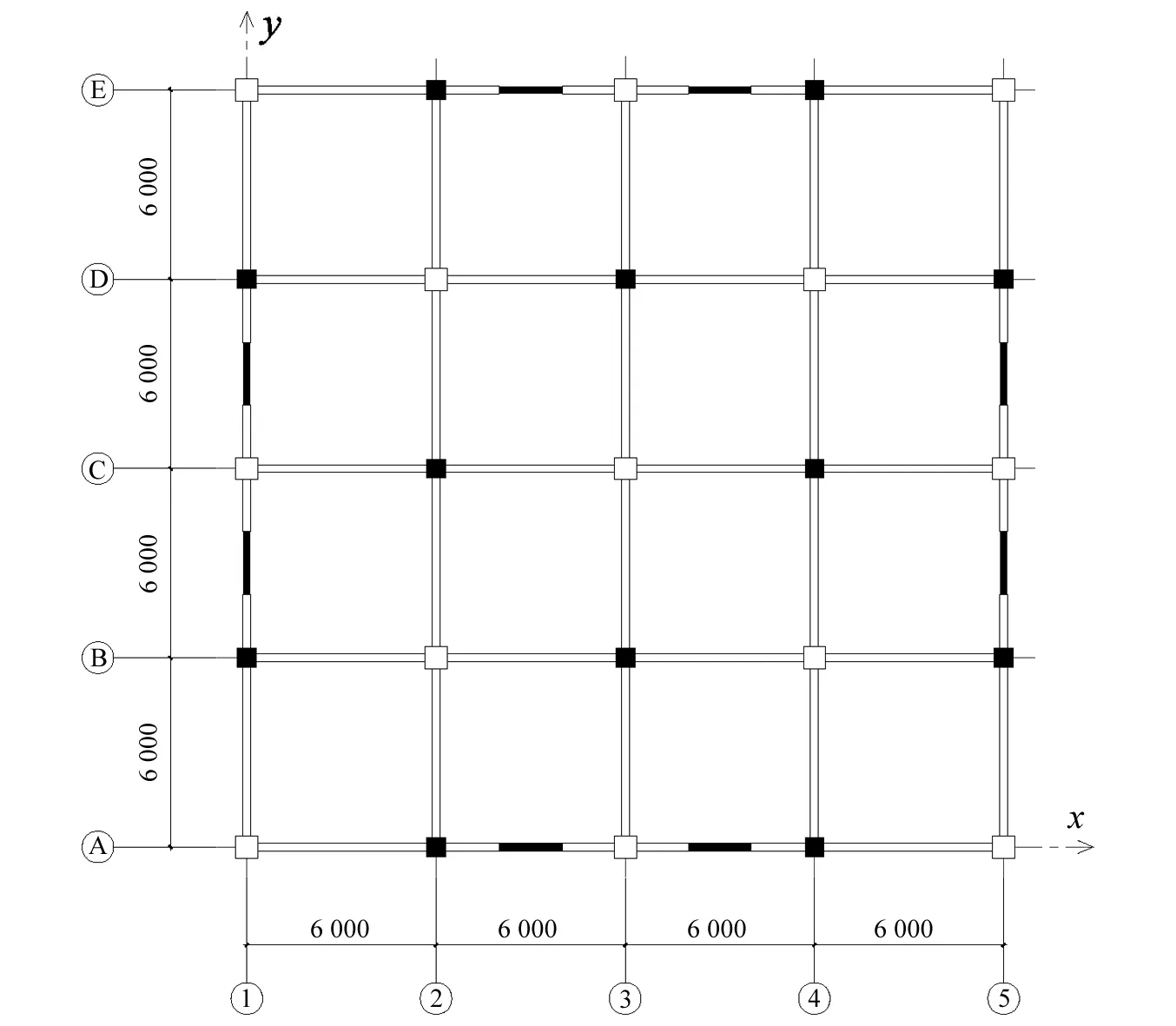
(□表示滑移柱，■表示常规柱，━表示剪力墙)图2 结构平面布置 (mm) Fig.2 Plan layout of structure (mm)

为进行对比，根据现行规范设计一个10层的常规框剪结构(结构二)。结构二的平面布置与结构一相同，具体设计结果如下：

梁、柱、墙的混凝土强度等级、框架梁和剪力墙的截面尺寸、剪力墙配筋，以及框架梁加密区的体积配箍率均同结构一。框架柱截面1～5层600 mm×600 mm/6～10层500 mm×500 mm。各层框架柱的纵筋配筋率0.8%～1.0%，加密区体积配箍率1.2%～1.4%。框架梁支座附近的顶面纵筋配筋率1.3%，跨中底面纵筋配筋率0.9%。结构二各层刚心与平面几何中心重合。

选择对应Ⅱ类场地的EL-Centro270°、Taft69°和SanFernando159°三条地震波作为结构X方向的地震输入，峰值加速度均调整为35 gal。计算过程中，时间步长取为0.02 s，总计算时间15 s。

考虑各层质心位置在Y方向-0.05l～0.05l范围内的20种非同步随机变化情况，具体抽样结果见表2。计算不同情况下结构一和结构二的地震反应，并与无偶然偏心时的相应计算结果进行对比。

表2 各层质心在Y方向的位置(×0.01l)Tab.2 Locations of mass centers for different stories inY-direction (×0.01l)

计算表明，三条地震波作用下结构一和结构二未考虑偶然偏心时顶层最大水平位移的平均值分别为15.5 mm和15.9 mm。表3所示为结构一和结构二考虑偶然偏心时顶层最大水平位移相对无偶然偏心时相应计算结果的增大幅度，从表中可以看出：

(1) 考虑偶然偏心时结构一顶层的弹性扭转反应略小于结构二。这是因为小震作用下结构一滑移柱顶端的摩擦支座尚未起滑，而滑移柱的截面尺寸大于结构二的框架柱，导致结构一的抗侧刚度和抗扭刚度均大于结构二的缘故。

(2) 各层质心位置均处于0.05l时，结构一和结构二的顶层弹性扭转反应略大于各层质心位置在±0.05l范围内随机分布时相应扭转反应的最大值。

表3 顶层最大水平位移的增大幅度Tab.3 Increment of top story’s maximum lateral displacement

2.3 周期比的影响

在结构一和结构二的其它参数保持不变的情况下，通过移动剪力墙位置或改变剪力墙截面参数，可实现不同的结构抗扭刚度与抗侧刚度之比。考虑图3和表4所示12种剪力墙位置及截面参数情况，其中(a)～(h)保持地震波输入方向(X方向)的结构抗侧刚度基本不变，只改变垂直地震波输入方向(Y方向)的剪力墙位置和截面参数，即只改变结构的抗扭刚度；(h)～(l)保持结构的抗扭刚度基本不变，只改变X方向的剪力墙截面参数，即只改变结构的抗侧刚度。表4中周期比为结构第一扭转周期与X方向第一侧向周期之比。

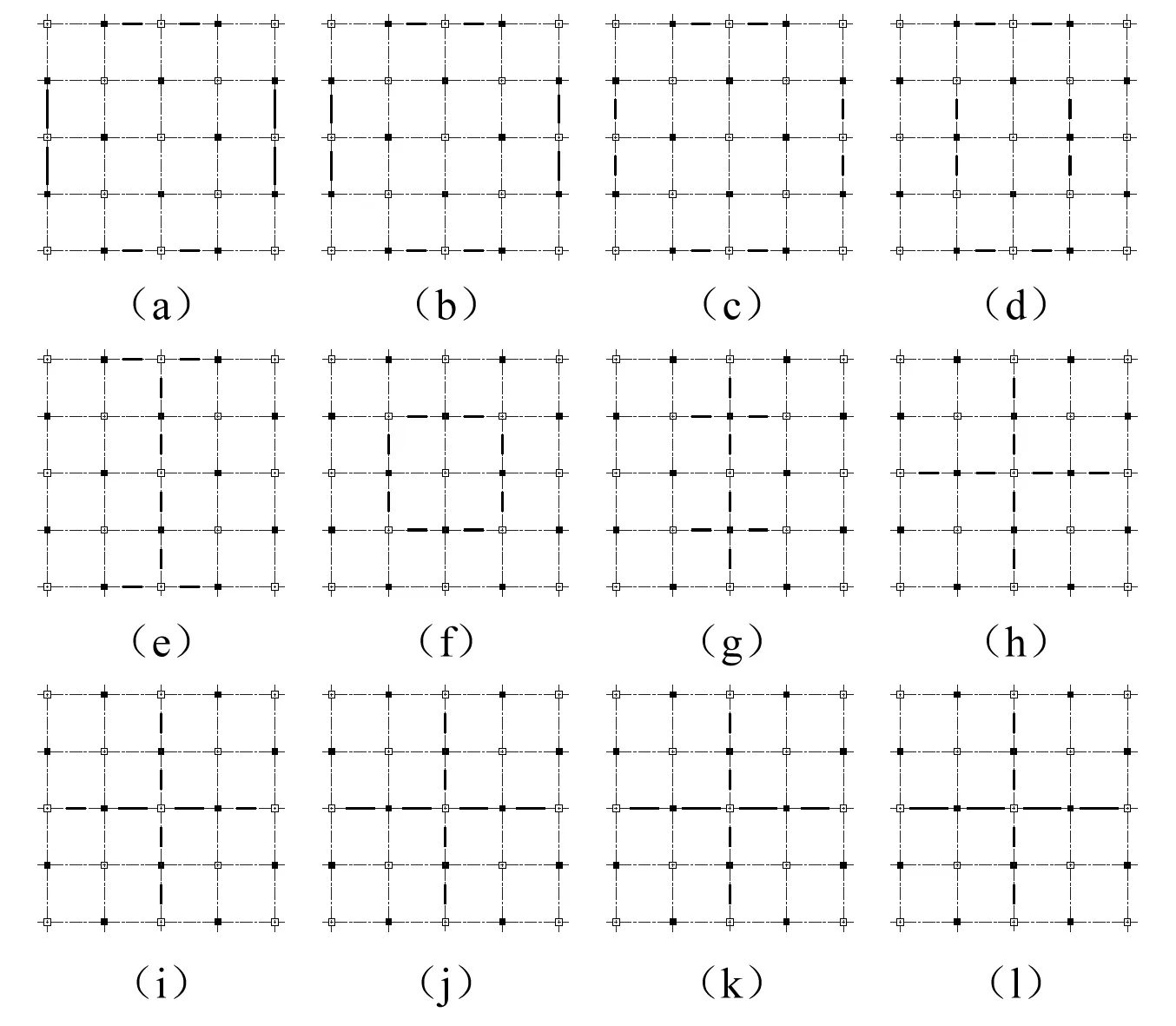
图3 剪力墙位置示意图 Fig.3 Schematic diagrams of shear walls

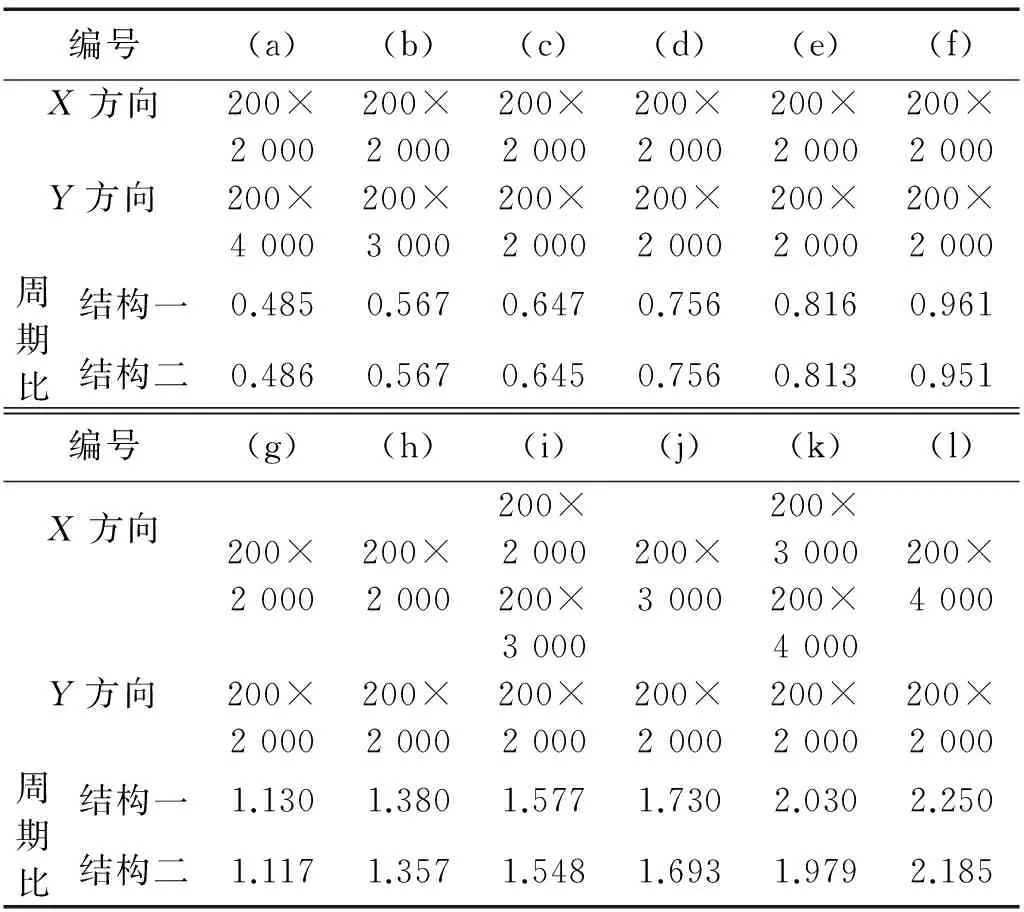
mm

考虑各层质心位置在Y方向0.05l的相同偶然偏心，针对图3和表4所示不同剪力墙位置及截面参数情况，分别计算结构一和结构二的地震反应，部分结果见图4和图5。图中每一条曲线均为三条地震波作用下的计算结果的平均曲线。从图中可以看出：

(1) 对于结构一，当周期比不超过0.8时，由扭转引发的顶层最大水平位移增大幅度随周期比增加呈现出上升的趋势，但未超1.20；当周期比超过0.9之后，顶层最大水平位移增大幅度总体呈现出先明显增加而后波动降低的趋势，并在周期比1.1左右达到最大值1.35。

(2) 对于结构一，当周期比不超过0.9时，顶层最大扭转角随周期比的增大而增大；周期比介于0.9～1.1时，该最大扭转角基本稳定；周期比超过1.1之后，该最大扭转角逐渐减小。

(3) 无论是顶层最大水平位移增大幅度还是顶层最大扭转角，结构二与结构一的变化趋势基本相同，二者相差5%以内。这表明小震作用下滑移柱顶端的摩擦支座尚未起滑时，周期比对部分柱顶滑移框剪结构扭转反应的影响规律与常规框剪结构几乎相同。

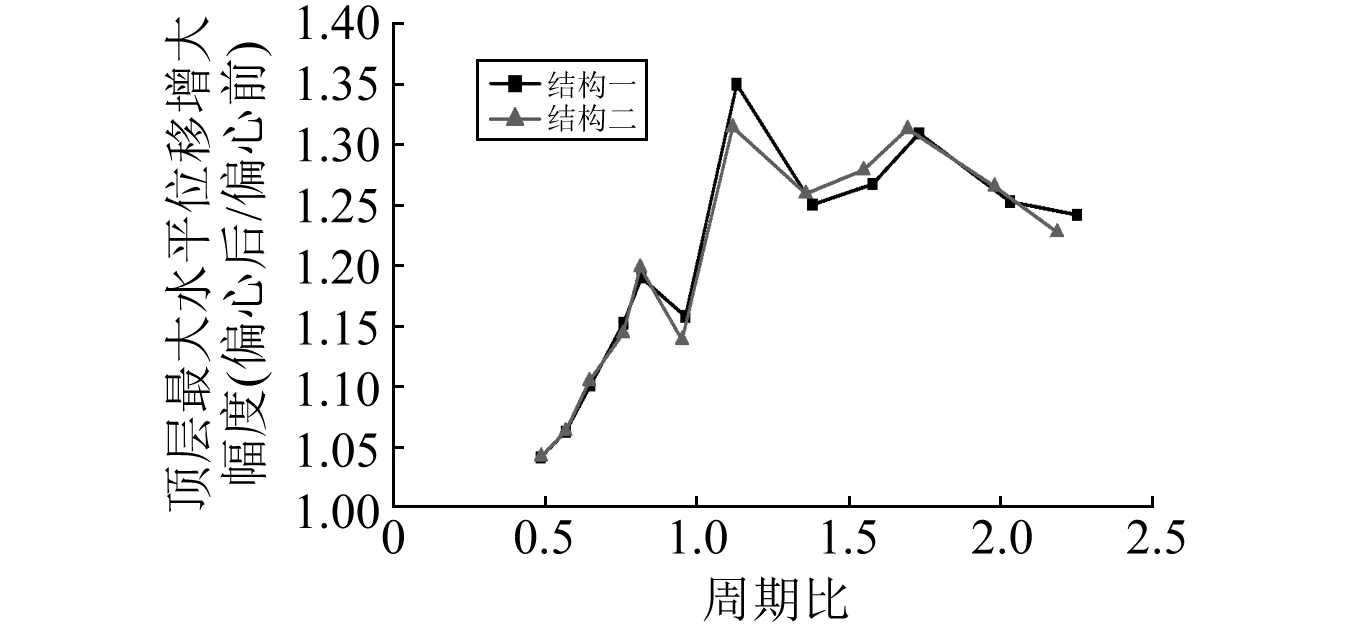
图4 周期比对结构顶层最大水平位移增大幅度的影响 Fig.4 Influence of period ratio on increment of top story’s maximum lateral displacement

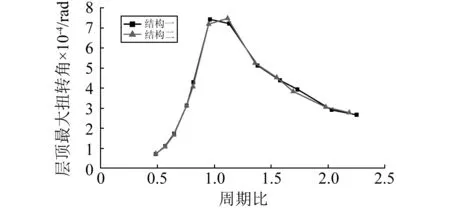
图5 周期比对结构顶层最大扭转角的影响 Fig.5 Influence of period ratio on top story’s maximum torsion angle

2.4 平面尺寸的影响

在结构一和结构二的其它参数保持不变的情况下，通过改变结构长宽比以考察平面尺寸对结构扭转反应的影响。考虑图6所示5种长宽比情况，以及3种剪力墙布置方案(注：不同布置方案中各层剪力墙的截面参数均为200 mm×2 000 mm)：①剪力墙布置在结构短边最外侧和长边外侧最中跨(见图6，方案1)；②剪力墙仅布置在结构短边最外侧，即图6中长边外侧的剪力墙取消(方案2)；③剪力墙布置在结构短边最外侧和长边外侧每一跨，即图6中长边外侧每跨均布置剪力墙(方案3)。对应不同剪力墙布置方案，结构一和结构二的周期比如表5所示。

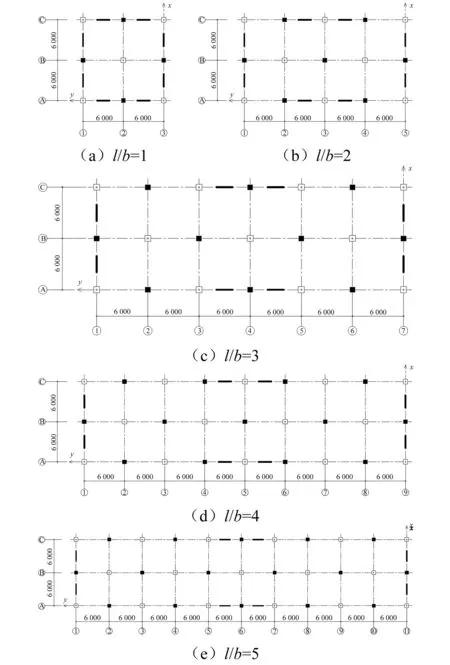
图6 结构平面示意图(mm) Fig.6 Schematic diagrams of plan layout of structure (mm)

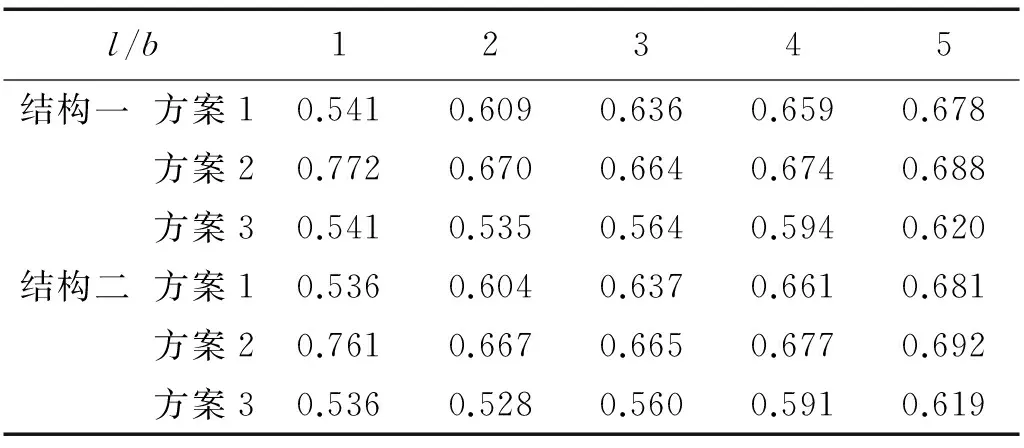
l/b12345结构一方案10.5410.6090.6360.6590.678方案20.7720.6700.6640.6740.688方案30.5410.5350.5640.5940.620结构二方案10.5360.6040.6370.6610.681方案20.7610.6670.6650.6770.692方案30.5360.5280.5600.5910.619

考虑各层质心位置在Y方向0.05l的相同偶然偏心，针对图6所示不同平面情况，分别计算结构一和结构二在X方向地震作用下的反应，部分结果见图7和图8。图中每一条曲线均为三条地震波作用下的计算结果的平均曲线。从图中可以看出：

(1) 对于结构一，在长宽比一定且周期比未超过0.9时，由扭转引发的顶层最大水平位移增大幅度总体呈现出随周期比增加而加大的趋势，这与前面第2.3节的研究结果一致；在周期比一定时，顶层最大水平位移增大幅度总体呈现出随结构长宽比增加而上升的趋势，且当结构长宽比在1～2之间变化时上升明显。

(2) 对于结构一，在长宽比一定且周期比未超过0.9时，由扭转引发的顶层最大扭转角总体呈现出随周期比增大而增大的趋势，这与前面第2.3节的研究结果一致；在周期比一定时，顶层最大扭转角呈现出随结构长宽比增加而先增后降的趋势，且长宽比等于2为分界点。

(3) 对应结构长宽比的不同取值，结构二的顶层最大水平位移增大幅度略高于结构一，但相差不超过5%，同时结构二的顶层最大扭转角与结构一非常接近。这表明小震作用下滑移柱顶端的摩擦支座尚未起滑时，结构长宽比对部分柱顶滑移框剪结构扭转反应的影响规律与常规框剪结构几乎一致。

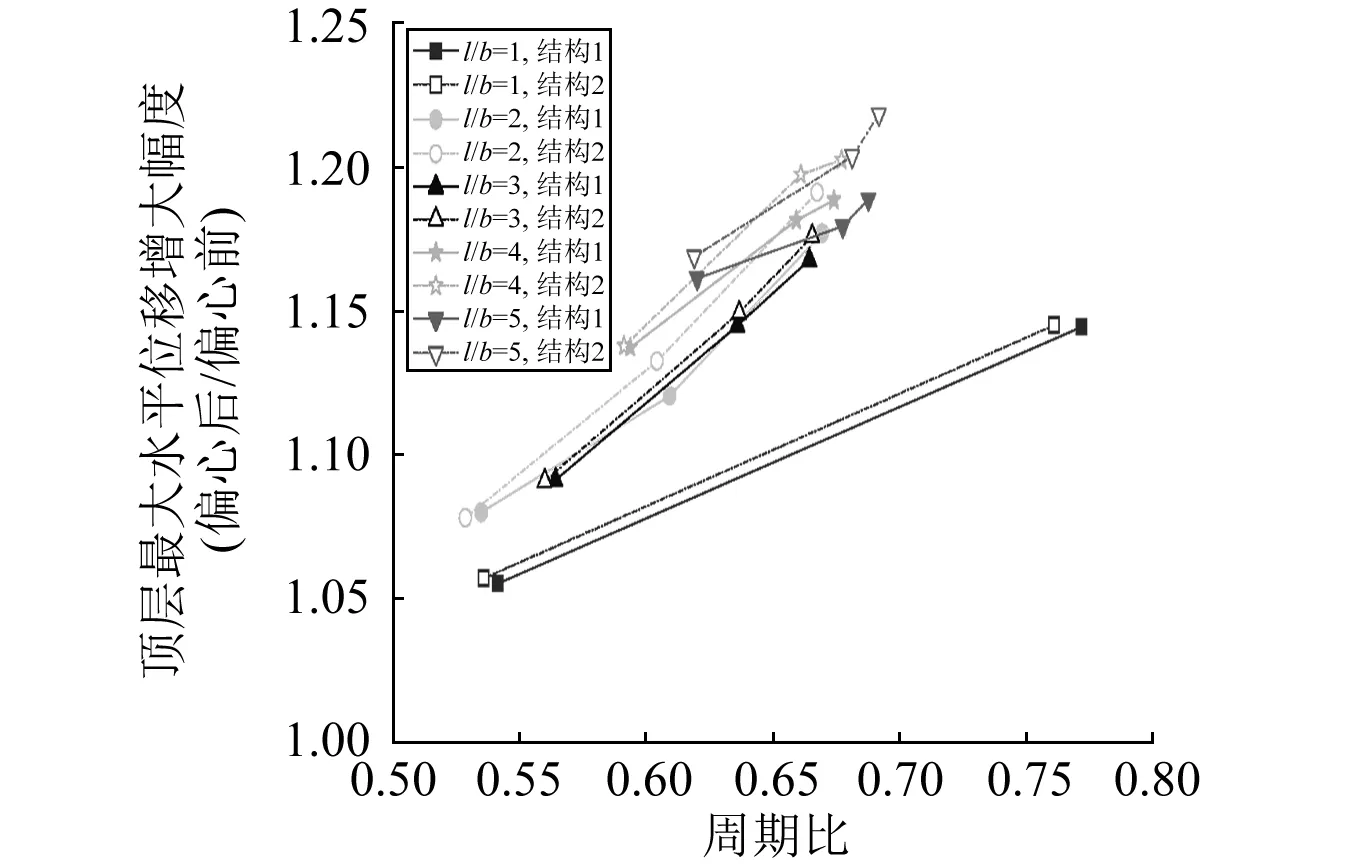
图7 长宽比对结构顶层最大水平位移增大幅度的影响 Fig.7 Influence of length-to-width ratio on increment of top story’s maximum lateral displacement

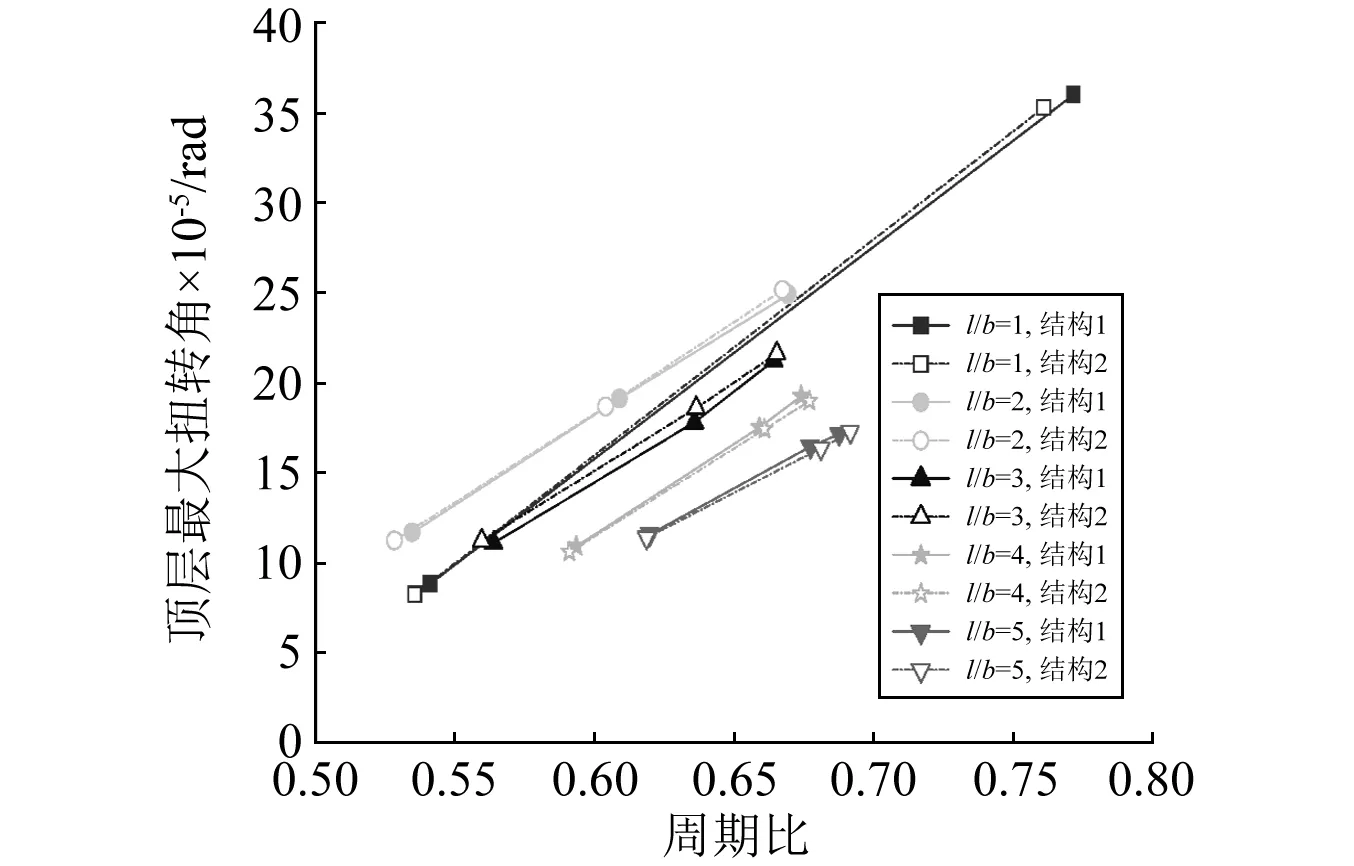
图8 长宽比对结构顶层最大扭转角的影响 Fig.8 Influence of length-to-width ratio on top story’s maximum torsion angle

2.5 设计建议

通过上述分析可以看出，考虑偶然偏心时部分柱顶滑移框剪结构的顶层最大水平位移相比未考虑偶然偏心时增大约5%～35%，因此在进行该类结构的抗震设计时应计及偶然偏心的影响。具体建议如下：

(1) 当结构长宽比不大于5且周期比小于0.9时，考虑偶然偏心的结构水平最大位移(即角点位移)比未考虑偶然偏心时偏保守地增大20%。

(2) 当结构长宽比等于1且周期比大于0.9时，考虑偶然偏心的结构水平最大位移(即角点位移)比未考虑偶然偏心时偏保守地增大35%。

上述建议与我国现行抗震规范[16]针对常规结构的相关规定较为接近。

3 偶然偏心导致的弹塑性扭转反应

3.1 计算模型

以前面第2.3节和第2.4节的结构为研究对象，采用通用软件Perform-3D对其进行大震作用下的弹塑性时程分析。梁、柱采用端部塑性铰区模型进行模拟，端部非线性截面采用纤维模型，其余部分为弹性截面，塑性铰区长度取为0.5倍的截面高度[17]。剪力墙采用宏观分层单元，即用一维纤维单元模拟墙的平面内压弯效应，用线性剪切本构模拟墙的平面剪切效应，墙的平面外弯曲、平面外剪切及扭转效应均采用弹性本构模拟。纤维截面定义时，以约束混凝土纤维和非约束混凝土纤维分别模拟端部约束区和非端部约束区。构件纤维截面的网格划分数量见表6。

表6 网格数量Tab.6 Number of meshes

混凝土的单轴受压本构采用修正Kent-Park应力-应变关系[18]，根据该模型计算得到不同构件中对应不同配箍率情况的混凝土本构关系(图9)。钢筋采用非屈曲本构关系，图10所示为本文所用钢筋的具体本构关系。计算过程中，混凝土强度和钢筋强度都采用平均值。

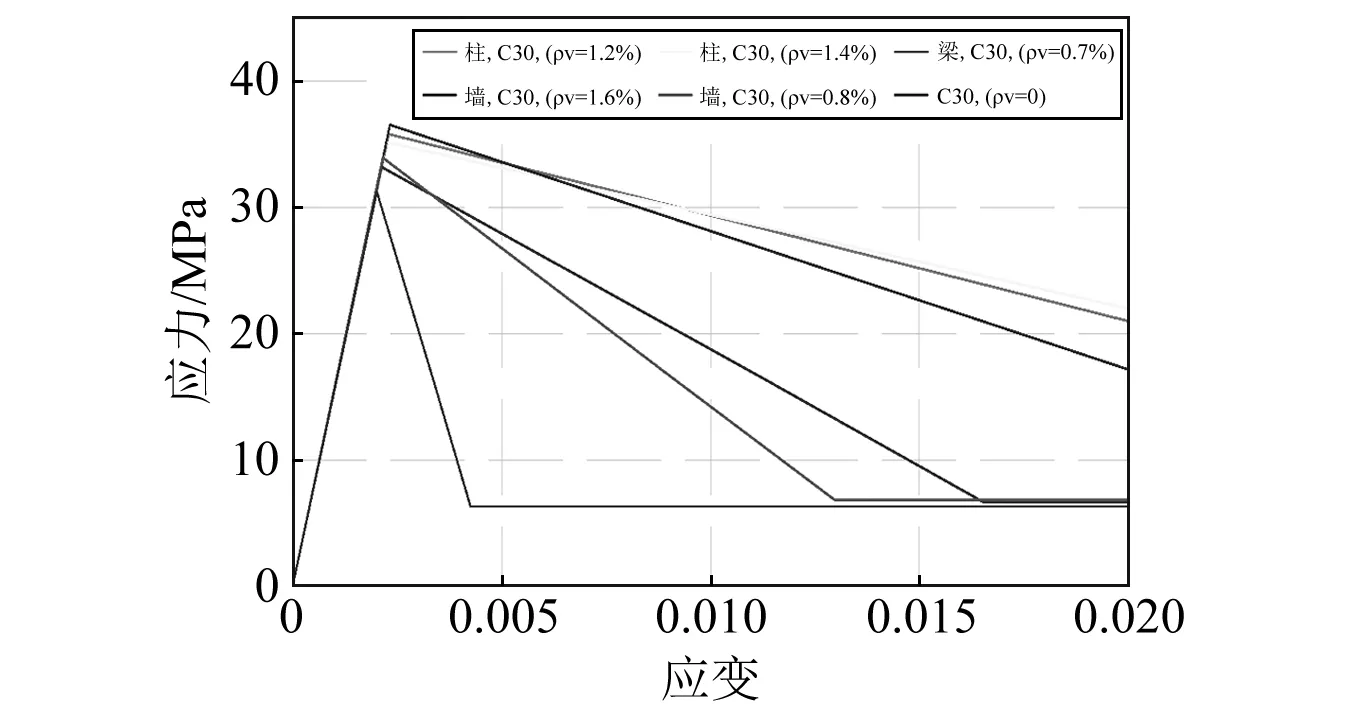
图9 不同体积配箍率(ρv)下的混凝土应力-应变关系 Fig.9 Relation between stress and strain of concrete with different transverse reinforcement ratios

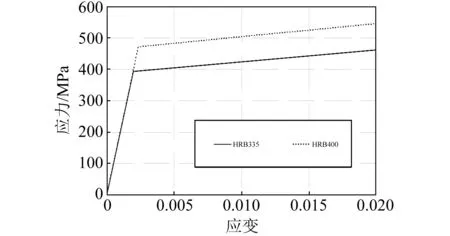
图10 钢筋的应力-应变关系 Fig.10 Relation between stress and strain of steel bar

Perform-3D中混凝土的恢复力模型如下：卸载刚度等于初始弹性刚度，再加载刚度通过人为指定的能量退化系数(介于0～1之间)自动计算。能量退化系数等于退化后滞回环面积除以无退化滞回环面积，如图11所示。本文计算中，混凝土的能量退化系数取为1。钢筋采用无退化双线性模型，即卸载刚度和再加载刚度都等于初始弹性刚度。

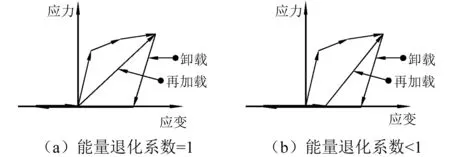
图11 混凝土材料的恢复力模型 Fig.11 Hysteresis loops of concrete

结构阻尼采用瑞利阻尼，第一及第二振型的阻尼比为0.05。三条输入地震波与前面小震弹性分析相同，但峰值加速度调整为220 gal。

3.2 周期比的影响

由于《高层建筑混凝土结构技术规程》[19]要求高层建筑结构的周期比不大于0.9，本节仅考虑图3和表4中周期比不超过0.9的剪力墙位置及截面参数情况。

考虑各层质心位置在Y方向0.05l的同步偶然偏心，分别计算结构一和结构二的地震反应，部分结果见图12和图13。图中每一条曲线均为三条地震波作用下的计算结果的平均曲线。从图中可以看出：

(1) 随周期比增加，大震作用下结构一和结构二的顶层最大水平位移增大幅度总体呈现出上升的趋势，但上升幅度相比小震时减小。

(2) 大震作用下结构一的顶层最大水平位移增大幅度相比结构二偏小，这是因为大震作用下结构一滑移柱顶端的摩擦支座起滑后消耗了部分地震输入能量，从而起到一定控制作用的缘故。

(3) 随周期比增加，大震作用下结构一和结构二的顶层最大扭转角总体上都逐渐增大，且具体数值相比小震时明显上升。

(4) 大震作用下结构一的顶层最大扭转角相比结构二偏小，且这一趋势随周期比的增大越发明显。

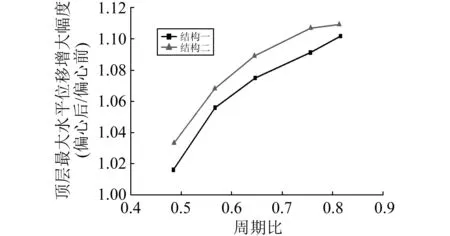
图12 大震下周期比对结构顶层最大水平位移增大幅度的影响 Fig.12 Influence of period ratio on increment of top story’s maximum lateral displacement under major earthquake

图13 大震下周期比对结构顶层最大扭转角的影响 Fig.13 Influence of period ratio on top story’s maximum torsion angle under major earthquake

针对图3(c)和(e)的剪力墙位置以及表4中对应的截面参数情况，考虑各层质心位置在Y方向0.05l的相同偶然偏心，大震作用下结构一和结构二各层的层间最大扭转角和层间最大位移角分别见图14和图15。图中每一条曲线均为三条地震波作用下的计算结果的平均曲线。从图中可以看出：

(1) 结构一各层的层间最大扭转角几乎都比结构二明显偏小，且结构一各层层间最大扭转角沿高度的分布相比结构二更为均匀。

(2) 除上部个别楼层以外，结构一各层的层间最大位移角均小于或非常接近结构二。

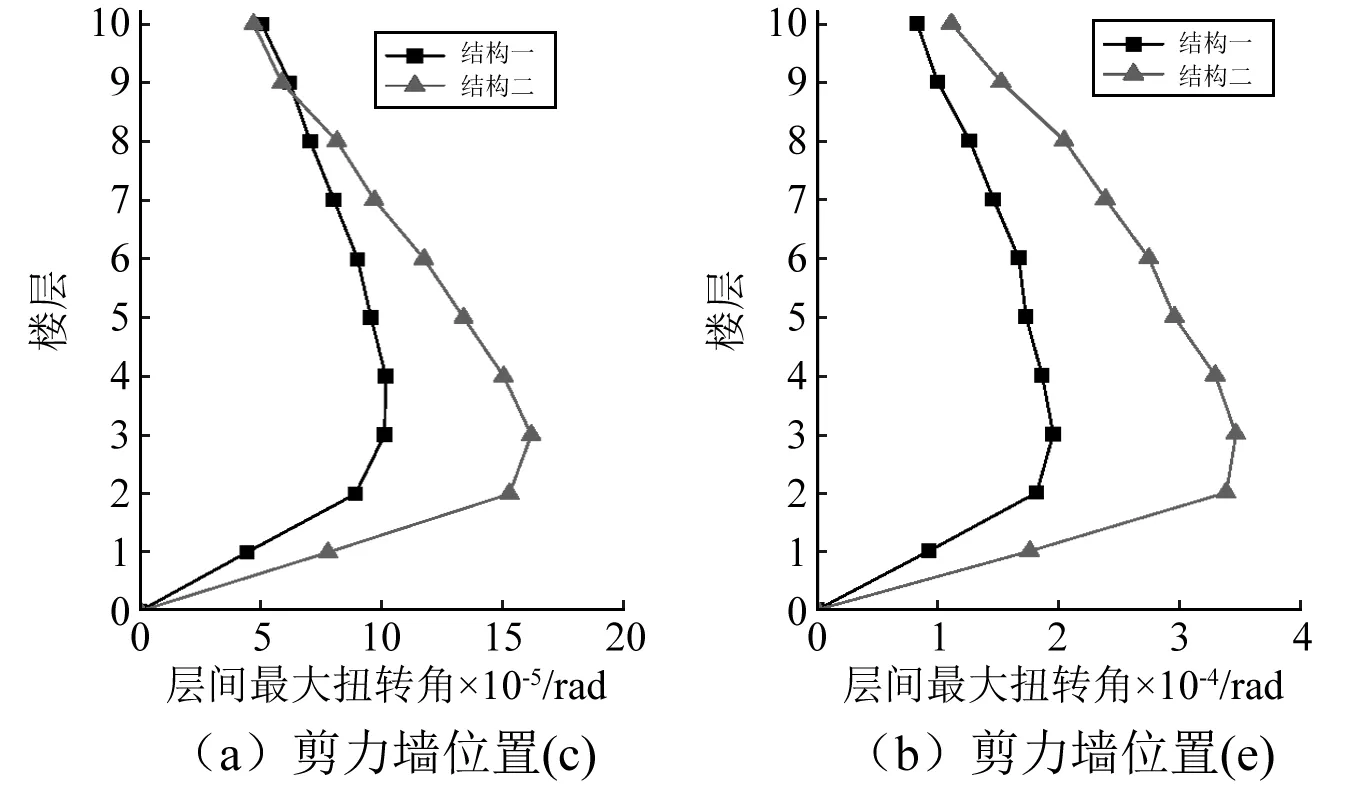
图14 大震下结构各层的层间最大扭转角 Fig.14 Maximum interstory torsion angles of different stories under major earthquake

图15 大震下结构各层的层间最大位移角 Fig.15 Maximum interstory drift ratios of different stories under major earthquake

3.3 平面尺寸的影响

考虑图6所示5种长宽比情况，以及第2.4节所述3种剪力墙布置方案，令各层质心位置存在Y方向0.05l的相同偶然偏心，分别计算结构一和结构二在X方向地震作用下的反应，部分结果见图16和图17。图中每一条曲线均为三条地震波作用下的计算结果的平均曲线。从图中可以看出：

(1) 对于结构一，在长宽比一定且周期比未超过0.9时，由扭转引发的顶层最大水平位移增大幅度总体呈现出随周期比增加而加大的趋势，这与前面第3.2节的研究结果一致；在周期比一定时，顶层最大水平位移增大幅度总体呈现出随结构长宽比增加而先增后降的趋势，且当结构长宽比在1～2之间变化时上升明显。

(2) 对于结构一，在长宽比一定且周期比未超过0.9时，由扭转引发的顶层最大扭转角总体呈现出随周期比增大而增大的趋势，这与前面第3.2节的研究结果一致；在周期比一定时，顶层最大扭转角呈现出随结构长宽比增加而减小的趋势。

(3) 结构二的顶层最大扭转角随长宽比的变化趋势与结构一类似。结构长宽比不大于2时，结构二的顶层最大扭转角与结构一非常接近；结构长宽比大于2时，结构二的顶层最大扭转角大于结构一。

图16 大震下长宽比对结构顶层最大水平位移增大幅度的影响 Fig.16 Influence of length-to-width ratio on increment of top story’s maximum lateral displacement under major earthquake

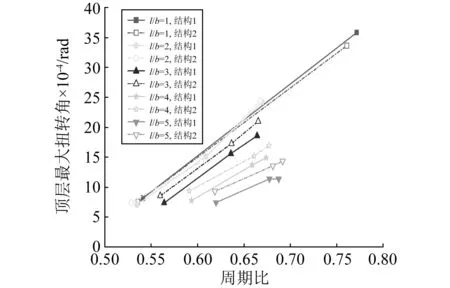
图17 大震下长宽比对结构顶层最大扭转角的影响 Fig.17 Influence of length-to-width ratio on top story’s maximum torsion angle under major earthquake

3.4 设计建议

通过上述分析可以看出，大震作用下考虑偶然偏心时部分柱顶滑移框剪结构的顶层最大水平位移相比未考虑偶然偏心时增大约5%～25%，因此在进行该类结构的大震验算时应计及偶然偏心的影响。具体建议为：当结构长宽比不大于5且周期比小于0.9时，考虑偶然偏心的结构弹塑性水平最大位移(即角点位移)宜比未考虑偶然偏心时偏保守地增大25%。

4 结 论

通过本文的研究，可得到如下初步结论：

(1) 考虑偶然偏心时，部分柱顶滑移框剪结构的顶层弹性扭转反应略小于常规框剪结构。

(2) 考虑偶然偏心时，周期比和长宽比对部分柱顶滑移框剪结构弹性扭转反应的影响规律与常规框剪结构几乎相同。

(3) 随着周期比的增加，大震作用下部分柱顶滑移框剪结构的顶层最大水平位移增大幅度总体呈现出上升的趋势，但上升幅度相比小震时减小；大震作用下该类结构的顶层最大水平位移增大幅度在多数情况下小于常规框剪结构。

(4) 随着结构长宽比的增加，大震作用下部分柱顶滑移框剪结构的顶层最大水平位移增大幅度总体呈现出而先增后降的趋势，且当结构长宽比在1～2之间变化时上升明显。

(5) 建议结构长宽比不大于5且周期比小于0.9时，考虑偶然偏心的部分柱顶滑移框剪结构的弹性水平最大位移比未考虑偶然偏心时偏保守地增大20%；而结构长宽比等于1且周期比大于0.9时，考虑偶然偏心的部分柱顶滑移框剪结构的弹性水平最大位移比未考虑偶然偏心时偏保守地增大35%。

(6) 建议结构长宽比不大于5且周期比小于0.9时，考虑偶然偏心的部分柱顶滑移框剪结构的弹塑性水平最大位移比未考虑偶然偏心时偏保守地增大25%。

[ 1 ] 胡庆昌. 1995年1月17日日本阪神大地震中神户市房屋结构震害简介[J]. 建筑结构学报, 1995, 16(3): 10-12.

HU Qingchang. Introduction of damage of building structures in Kobe Earthquake on 17 January 1995 [J]. Journal of Building Structures, 1995, 16(3): 10-12.

[ 2 ] 温增平, 徐超, 陆鸣, 等. 汶川地震重灾区典型钢筋混凝土框架结构震害现象[J]. 北京工业大学学报, 2009, 35(6): 753-760.

WEN Zengping, XU Chao, LU Ming, et al. Damage features of R.C frame structures in wenchuan earthquake [J]. Journal of Beijing University of Technology, 2009, 35(6): 753-760.

[ 3 ] 吴波, 王明君. 混凝土空间板柱结构的震致落层倒塌分析[J]. 华南理工大学学报(自然科学版), 2012, 40(2): 1-6.

WU Bo, WANG Mingjun. Analysis of pancake collapse of RC space slab-column structures under earthquake [J]. Journal of South China University of Technology (Natural Science Edition), 2012, 40(2): 1-6.

[ 4 ] 吴波, 黄仕香, 赵新宇. 混凝土框剪结构的落层倒塌碰撞试验[J]. 工程力学, 2012, 29 (6): 176-187.

WU Bo, HUANG Shixiang, ZHAO Xinyu. Experimental study on pancake collapse of RC frame-shear wall structures [J]. Engineering Mechanics, 2012, 29(6): 176-187.

[ 5 ] HAWKINS N M, MITCHELL D. Progressive collapse of flat plate structures [J]. ACI Journal, 1979, 76(7): 775-808.

[ 6 ] ASTANEH-ASL A. Progressive collapse prevention in new and existing buildings [C]. Proc. Of the 9th Arab Structural Engineering Conf. Abu Dhabi, UAE. 2003: 1001-1008.

[ 7 ] 吴波, 陈展图. 抗倒塌柱顶部分滑移钢筋混凝土框架结构的初步研究[J]. 地震工程与工程振动, 2008, 28(4): 82-87.

WU Bo, CHEN Zhantu. Preliminary study on RC frame structures with sliding at partial column upper ends for preventing collapse [J]. Earthquake Engineering and Engineering Vibration, 2008, 28(4): 82-87.

[ 8 ] 吴波, 吕文龙, 熊伟. 部分柱顶滑移钢筋混凝土框剪结构[J]. 工程力学, 2011, 28(4): 82-88.

WU Bo, LÜ Wenlong, XIONG Wei. RC frame-shear wall structures with partial columns sliding at upper ends [J]. Engineering Mechanics, 2011, 28(4): 82-88.

[ 9 ] 吴波, 吕文龙. 部分柱顶滑移钢筋混凝土框剪结构的深化研究[J]. 工程力学, 2012, 29(8): 143-149.

WU Bo, LÜ Wenlong. Research on RC frame-shear wall structures with partial columns sliding at upper ends [J]. Engineering Mechanics, 2012, 29(8): 143-149.

[10] 吴波, 吕文龙, 沈朝勇. 部分柱顶滑移钢筋混凝土框剪结构的试验研究[J]. 工程力学, 2015, 32(2): 163-170.

WU Bo, LÜ Wenlong, SHEN Chaoyong. Experimental study on RC frame-Shear wall structure with partial columns sliding at upper ends [J]. Engineering Mechanics, 2015, 32(2): 163-170.

[11] 吴波, 吕文龙. 部分柱顶滑移钢筋混凝土结构的滑移柱P-δ效应[J]. 华南理工大学学报 (自然科学版), 2016, 44(2): 1-7.

WU Bo, LÜ Wenlong. Study on P-δ effect of sliding columns in RC structures with partial columns sliding at upper ends [J]. Journal of South China University of Technology (Natural Science Edition), 2016, 44(2): 1-7.

[12] 吕文龙. 部分柱顶滑移钢筋混凝土框剪结构的简化分析[J]. 地震工程与工程振动, 2016, 36(3): 178-186.

LÜ Wenlong. Simplified analysis of RC frame-Shear wall structure with partial columns sliding at upper ends [J]. Earthquake Engineering and Engineering Dynamics, 2016, 36(3): 178-186.

[13] Computer and Structures Inc. Perform component and element [M]. Berkeley: Computer and Structures Inc. 2006.

[14] PARK Y J, WEN Y K, ANG A H S. Random vibration of hysteretic systems under bi-directional ground motions [J]. Earthquake Engineering & Structural Dynamics, 1986, 14(4): 543-557.

[15] CONSTANTINOU M, MOKHA A, REINHORN A. Teflon bearings in base isolation-Part Ⅱ: Modeling [J]. Journal of Structural Engineering, ASCE, 1990, 116(2): 455-474.

[16] 建筑抗震设计规范: GB 50011—2010 [S]. 北京: 中国建筑工业出版社, 2010.

[17] PAULAY T, PRIESTLEY M J N. Seismic design of reinforced concrete and masonry buildings [M]. New York: John Wiley & Sons, Inc, 1992.

[18] SCOTT B D, PARK R, PRIESTLEY M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates [J]. ACI Journal, 1982, 79(1): 13-27.

[19] 高层建筑混凝土结构技术规程: JGJ 3—2010 [S]. 北京: 中国建筑工业出版社, 2010.

[20] Technical specification for concrete structures of tall building: JGJ 3—2010 [S]. Beijing: China Architecture & Building Press, 2010.