基于Matlab的灰色线性回归模型在高层建筑监测中的应用

2018-05-02岁秀珍刘坚耿吴建中

浙江水利水电学院学报 2018年1期

陈浩，岁秀珍，刘坚耿，吴建中

(1.义乌市大地数字测绘有限公司,浙江义乌 322000；2.义乌市勘测设计研究院,浙江义乌 322000)

随着我国城市化进程的加快，城市空间愈发拥挤，可用空地越来越少，房屋的层数不断攀升，随之而来，建设工程的施工与监测难度愈发增加.进入新世纪以来，各项监测仪器及手段不断应用到监测工程中来[1-3]，但还是会发生高层建筑倒塌的事故.运用各种新型仪器监测的同时，如何有效地对取得的监测数据进行高效地预测分析，往往是各国学者研究的课题，直至目前，尚无一高精度预测模型可以运用于各类监测工程中[4].1969年Bate和Granger提出将不同模型根据自身特点有选择性进行组合[5]，可以弥补单一模型的不足，提高预报精度.从此，组合式模型成为各国学者的研究热点课题，在施工监测中，也被广泛地运用，以此作为施工决策的重要依据.

建筑变形测量规范(JGJ8-2016)在“8.4建模和预报”中明确提出线性回归模型和灰色系统理论模型的基础上组合而成的新型模型.[6]它既具有线性回归模型的特点又具有灰色模型对贫数据的处理能力.结合实际工程分析可知，采用两者组合而成的模型在预测精度上有显著地提高，预测的可靠性和稳定性也高于单一的预测模型.在无外力施加作用下，因自身承重引起的高层建筑物沉降，灰色线性回归模型有着广泛地应用前景.

1 灰色线性回归组合模型

组合式模型应充分考虑单一模型的数学函数结构，从其结构出发建立组合方式.灰色线性回归(GMXX)组合模型是从灰色模型和回归模型各自的结构出发建立起来的，其模型建立原理如下[7]：

根据灰色GM(1,1)模型函数式为：

(1)

将式改写为如下方程式：

(2)

(3)

式中，c1,c2,c3,v为待定参数.

为确定待定参数，现构造如下方程式：

(4)

令

ym(t)=z(t+m)-z(t)=c1evt(evm-1)(ev-1)

(5)

ym(t+1)=z(t+m+1)-z(t+1)=
c1ev(t+1)(evm-1)(ev-1)

(6)

式(6)与式(5)两式相除，ym(t+1)/ym(t)=ev，即参数v的解为：

v=ln(ym(t+1)/ym(t))

(7)

z(t)=x(1)(t+1)-x(1)(t),(t=1,2,…,n-1)

(8)

式(7)中m取不同的值，v的计算值将不同：

当m=1时，得

y1(t)=z(t+1)-z(t),(t=1,2,…,n-2)

v1(t)=ln(y1(t+1)/y1(t)),(t=1,2,…,n-3)

当m=2时，得

y2(t)=z(t+2)-z(t),(t=1,2,…,n-3)

v2(t)=ln(y1(t+1)/y1(t)),(t=1,2,…,n-4)

当m=n-3时，得

yn-3(t)=z(t+n-3)-z(t),(t=1,2)

vn-3(t)=ln(y1(t+1)/y1(t)),(t=1)

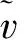
(9)

c=(ATA)-1ATx(1)

(10)

于是可以生产一次累加序列的时间响应函数为：

(11)

将式(11)的计算值进行一次累减，生成新的序列即为原始序列x(0)的拟合值和灰色线性回归组合模型的预测值.

当c1=0时，式(2)～式(11)为一元回归方程式；当c2=0时，式(11)为灰色GM(1,1)模型.由此充分说明灰色线性回归组合模型是回归模型与灰色模型运用串联的组合方式构成的预测模型.

2 模型精度检验

对模型精度的评定方法最常用的有：残差检验法、后验方差检验法和关联度检验法[8].残差检验法是根据模型拟合值与原序列值进行逐个检验；后验方差检验是对拟合残差运用概率统计的方法进行检验，主要由均方差比值C和小误差概率p表达；关联度检验是基于拟合模型值与建模序列曲线的相似度进行检验，主要采用前两种检验方法.

(1)残差检验

残差序列为：

(12)

相对残差为：

(13)

(2)后验方差检验

原始数据序列X(0)的均值与方差为：

(14)

残差序列ε(0)的均值与方差为：

(15)

均方差比值C为：

C=S2/S1

(16)

小误差概率p为：

(17)

通过式(15)～式(17)计算相对误差Δ，均方差比值C，小误差概率的值p，通过查询可以确定灰色模型拟合精度的等级(见表1).

表1 模型检验等级

3 MATLAB编程实现灰色线性回归模型

MATLAB具有强大的运算与编程能力，灰色线性回归组合模型的计算量比较大，运用MATLAB模型编写相应的计算程序，可以计算出相应的拟合值和预测值，大大缩短了计算时间，提高了准确度[9].方便监测数据的处理，通过读取指定模板的.xls格式，可以输出预制的监测成果数据表，能够直观的显示拟合值、预测值、拟合残差及预报等级，软件界面(见图1).

图1 软件界面

灰色线性回归组合模型的核心代码如下：

nn1=input(‘请输入需要预测的期数=’);

x0=input(‘请输入已有实测的期数数据(以行向量输入) x0=’);

for i=1:size(x0,2)

acu=0;

for k=1:i

acu=acu+x0(k);

end

x1(i)=acu;

end

for j=1:(size(x0,2)-3)

for i=1:(size(x0,2)-j-2)

v=log((x1(i+j+2)-x1(i+j+1)-x1(i+2)+x1(i+1))/(x1(i+j+1)+x1(i)-x1(i+1)-x1(i+j)));

a(i,j)=v;

end

n=size(x0,2);

v1=2*sum(sum(a))/((n-2)*(n-3));

lt=zeros(1,n);

for k1=1:n

l=exp(v1*k1);

lt(k1)=l;

end

aa1=ones(n,1);

aa2=zeros(n,1);

for kk=1:n

n1=kk;

aa2(kk)=n1;

end

aa=[lt' aa2 aa1];

c=inv(aa'*aa)*aa'*x1';

for i=1:(n+nn1)

xx=c(1)*exp(v1*i)+c(2)*i+c(3);

xx1(i)=xx;

end

4 工程案例

本文选取义乌经济开发区总部经济A组团工程，共8幢高层建筑，其中2幢为超过100 m的超高层.项目所涉及基坑均为一级基坑.从施工监测开始，选择其中40期房屋沉降监测数据，具体监测数据(见表2).

将前30期数据作为分析样本，对后10期数据进行预测，分别采用线性回归模型、灰色模型、灰色线性回归模型进行拟合预测，后10期数据预测数据(见表3).

表2 沉降数据

表3 三种模型预报值对比表

由表3分析可知，经模型精度检验，三种模型等级均为一级.但在预测精度方面，线性回归模型最小为0.298%，最大为1.163%；灰色模型最小为0.232%，最大为2.984%；灰色线性回归模型最小为0.007%，最大为0.752%.随着预报期数增多，线性回归模型和灰色模型预测的精度有减弱趋势，而灰色线性回归模型整体预报精度比较平稳.