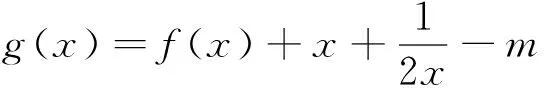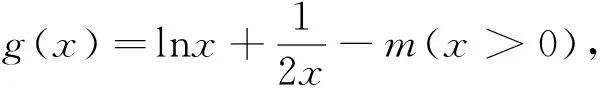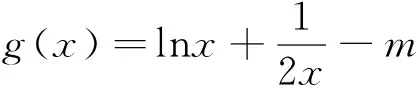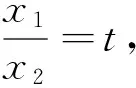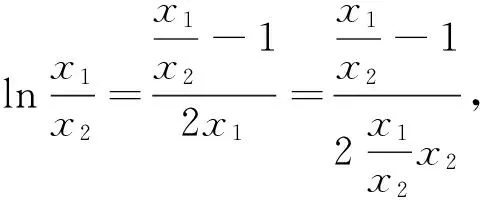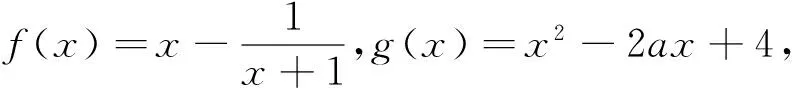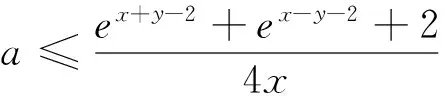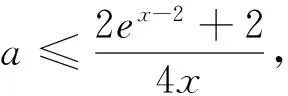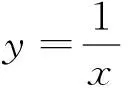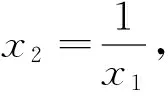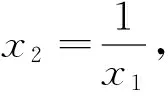让函数导数双变量问题“有法可依”

曾继成 邱 云

厦门大学附属实验中学 (363123)

函数导数是每年高考的热点与难点．在近几年各地高考试卷中，频繁出现导数中含双变量的问题．此类题型因含有两个变量，思维量大，解题方法灵活，对学生的数学抽象、数学建模等核心素养提出了很高要求．在有限的时间内，考生要完成模型分析，提炼成自己熟悉的函数背景，是有很大难度的．因此这类题型常常成为选拔优秀人才，评判学生数学核心素养高低的压轴题．笔者结合自己的教学体验，针对这类“双变量问题”总结了几种常见的解题策略，供大家参考．

策略一、利用函数单调性

例1 已知函数f(x)=(x-2)ex+a(x-1)2有两个零点．

(Ⅰ)求a的取值范围；

(Ⅱ)设x1,x2是f(x)的两个零点，证明：x1+x2<2(2016年全国卷Ⅰ卷21题)．

试题分析：第一问考查学生分类讨论的数学思想，对中等及中等以下水平的考生是个不小的考验，此处不涉及双变量问题，略．而第二问不难看出是一道典型的“双变量”极值点偏移问题，对于熟悉极值点偏移问题解题策略的考生，不算难题．

解题思路如下：

思路一：不失一般性设x1

又∵由(1)知f(x)在(-∞,1)内单调递减，

∴x1+x2<2等价于f(2-x2)

思路二：《中学数学教学参考》(上旬)2014年第7期，邢友宝老师的文章《极值点问题的处理策略》，不难构造出新函数：

F(x)=f(1+x)-f(1-x)=[(x-1)e1+x+ax2]-[(-1-x)e1-x+ax2]=(x-1)e1+x+(1+x)e1-x(x>0),求导后讨论单调性易得f(1+x)>f(1-x)．再结合题目条件f(x1)=f(x2)，并适当变形可得，f(x1)=f(x2)=f[1+(x2-1)]>f[1-(x2-1)]=f(2-x2)．

最后利用(Ⅰ)的结论，由函数在区间(-∞,1)上的单调性证得x1<2-x2，从而得到x1+x2<2.

策略二：整体代换

例2 已知函数f(x)=lnx-ax.

(Ⅰ)若函数f(x)在(1,+∞)上单调递减，求实数a的取值范围；

试题分析：第(Ⅰ)问比较常规，不再赘述．第(Ⅱ)问明显也是极值点偏移的问题，仍然可以利用邢友宝老师文章中提出的构造函数的方式予以解决，方法与上述例题1的思路二如出一辙，不再详细阐述．本题主要介绍另外一种处理方式，解题思路如下：

接来下只要能用含t的表达式表示x2，则问题就转化为跟t有关的不等式，就能达到减少变量的目的了．

而由上述的(*)式可容易变形得到

策略三：分成主次元思想

试题分析：本题是一道很常规的题目，题干中涉及了两个变量，也是一种含双变量问题的典型例题，解此类题型的主流思想就是分成主次元考虑，解法思路如下：

因为对任意x1∈[0,1]，不等式f(x1)≥g(x2)都要成立，所以先将x2看成是一个常数，则不等式等价于f(x1)min≥g(x2)，x∈[0,1]．而根据函数的解析式，容易求得f(x)min=-1．所以原命题转化为存在x2∈[1,2]，使得g(x2)≤-1．此时成功将变量x1去掉，整道题就变成一道很常规的单变量问题．整个过程，运用了主次元思想，成功避开了同时讨论两个变量带来的麻烦，是一种比较常见的处理方式．再比如看下面的这道客观题，若运用主次元思想，同样会收到事半功倍的效果．

例4 若对∀x,y∈[0,+∞),不等式4ax≤ex+y-2+ex-y-2+2恒成立，则实数a的最大值是多少？

策略四：巧妙运用“对称性”

综上几种题型的常见处理策略，虽然方式各异，但是最核心的问题都是降元．具体怎么降，如何提高学生的该类型题的解题能力，笔者认为一个重要的举措就是在解题教学中要培养学生的数学素养，让其在解题过程中，熟悉各种题型的特点和关键点，再综合自身的数学知识和解题经验，在解题思想的指导下，逐步学会分析题意，透析本质，找到已知与未知的桥梁，最终成功解决问题．