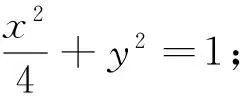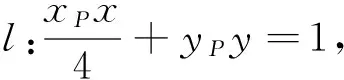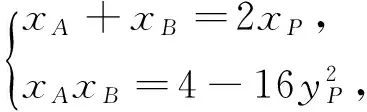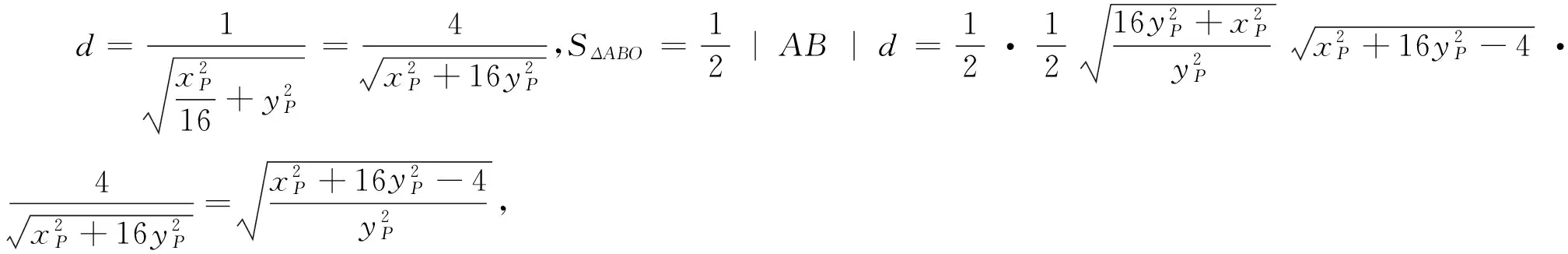多角度认识圆锥曲线的切线

杨艳萍

江西省九江第一中学 (332000)

新课标中的“四基”强调，学生通过数学学习，不仅要获得数学“基础知识”和“基本技能”，还要获得数学“基本思想”和积累“基本活动经验”.因此，在高中数学教学活动中，引导学生在探究过程中积累数学活动经验，应渗透到教学的方方面面.本文，首先引导学生自己动手体验二次曲线在一点处切线的形成过程，由此推导出二次曲线在一点处的切线.其次，利用一般到特殊的数学基本思想得到圆锥曲线在一点处的切线方程.然后，结合圆锥曲线定义和角平分线等基础知识推导出圆锥曲线的切平分线.最后，将一点处切线方程和切平分线应用到具体解题中.

1.从定义入手，推导切线方程

学生动手在纸上画一条二次曲线，曲线上一点P，过点P作直线交曲线于点Q，让学生将尺子与直线PQ重合，当点Q沿着曲线向点P靠近时，学生用手推动尺子绕着点P旋转，当点Q无限的靠近点P时，尺子由曲线的割线趋近于点P处的切线.学生通过自己动手体验二次曲线切线的形成过程，能直观的得到结论：曲线在点P处切线的斜率是当点Q沿着曲线无限趋近点P时，割线PQ的斜率.

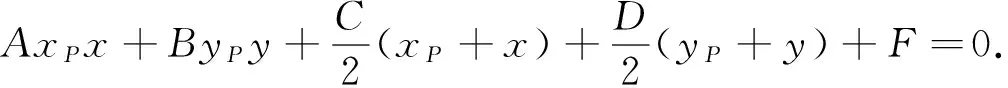
证明：设过点P的直线交曲线E于点Q(xQ,yQ)，则

由(1)-(2)得

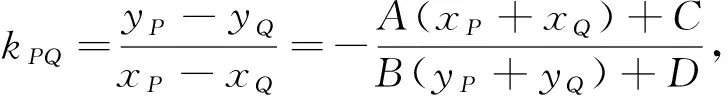
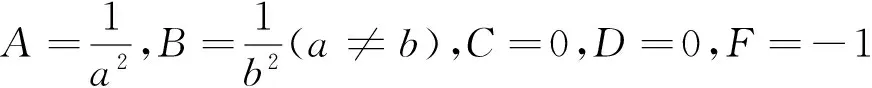
由推论得以下结论(简称：代一半留一半)：

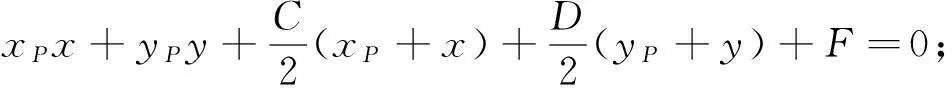
特别地圆E：(x-a)2+(y-b)2=R2在点P(xP,yP)处的切线方程为(x-a)(xP-a)+(y-b)(yP-b)=R2；

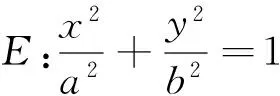
(4)抛物线E：x2=2py在点P(xP,yP)处的切线方程为xPx=p(yP+y).

2.从几何入手，探究切线性质

圆锥曲线切线的性质很多，限于篇幅，本文仅讨论圆锥曲线的切平分线：

(1)抛物线E：y2=2px(p>0)的焦点为F，P是抛物线E上任意一点，则抛物线E在点P处的切线与直线PF倾斜角的角平分线平行.

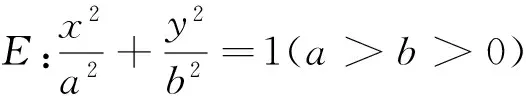
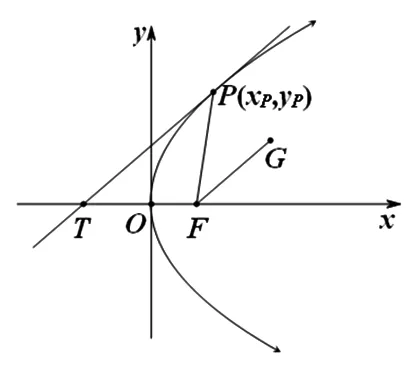
图1

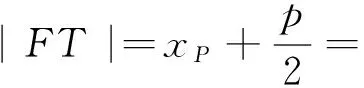
即抛物线E在点P处的切线与直线PF倾斜角的角平分线平行.

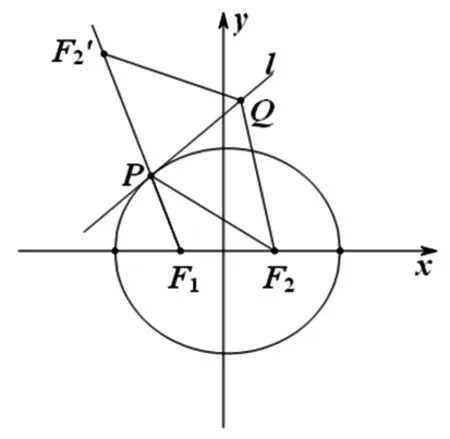
图2

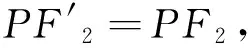
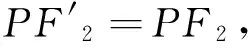
(3)证明与(2)相似.

3.从试题入手，强化切线的应用.

切线的应用，主要围绕几何性质与代数方程这两个方面，有时需要两者兼顾.

3.1 切线几何性质的应用

例1 已知抛物线y2=2px(p>0)的焦点为F，P是抛物线上任意一点，过F作抛物线在点P处的切线的垂线，垂足为点Q，求证：点Q在定直线上.

分析：解析几何问题就是几何问题，应结合图像理顺各条件之间的关系.本题中抛物线上任意一点P处的切线都与直线PF倾斜角的角平分线平行,从平行线入手，借助平行线的性质，便可得到FT=PF，从而推出点Q在定直线y轴上.

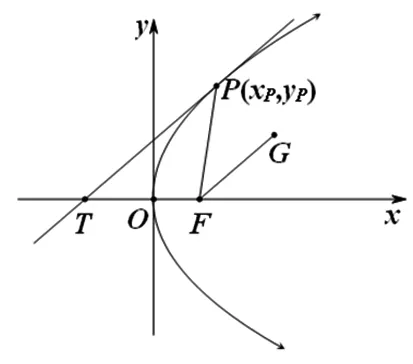
图3

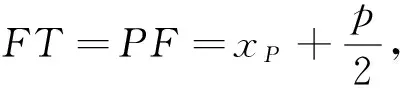
分析1：充分利用几何条件，发现几何规律，是研究几何问题的重要之举.在几何图形中，有关几何要素之间的关系，有很多优美的性质，其中一类性质是：随着某些要素位置或数量的改变，其他某些要素会表现出不变性.

本题中ΔFAB的周长就不随着直线AB的改变而改变，从该定值入手，借助三角形三边关系，便可求|AB|的最大值.

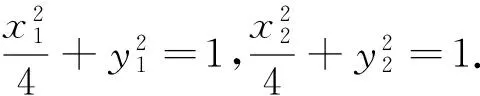
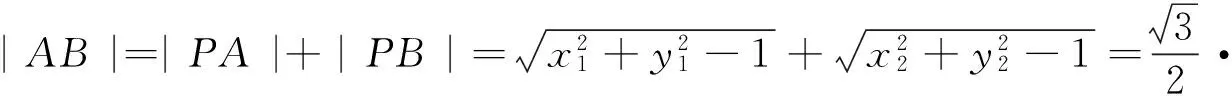
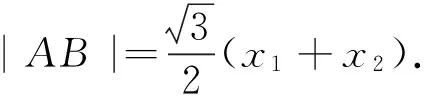
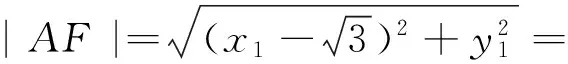
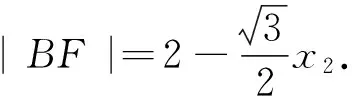
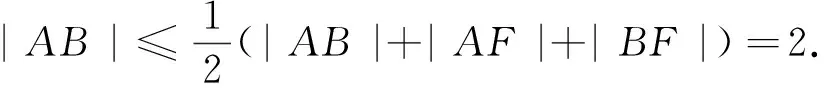
3.2 切线方程的应用

分析2:由上知例2解题的关键是：如何处理三个图形的位置关系，在此过程中，三个点(A,B和切点)的恰当使用是关键中的关键.从题目问题来看，题目考查运动变化过程中，变量之间的函数关系，如何构造函数关系和如何求最值，是解决本题的两个重要环节，首先需要解决构造函数的问题，最值则需要视函数形式而定.

显然，一切变化皆因m而起！m的变化必导致切线AB的变化，所以线段AB的长一定是参数m的函数.有了这个信念，我们就可以自信地一步一步地将各有关的量用参数m表示，最后即可得到|AB|关于参数m的函数，求这个函数的最大值即可完成解题任务.

假设各个要素的构造顺序是：切点P——切线l——交点A,B——弦AB.因此可以从设圆的切线入手，其与椭圆相交成弦AB，将弦长|AB|表示为变量m的函数，再求弦长的最大值.

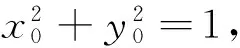
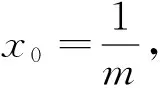
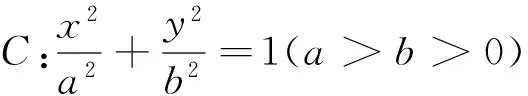
(1)求椭圆C的方程；

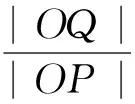
分析：解决本题(2)(ⅱ)的关键是：如何处理三个点(A,B和切点P)的关系是关键.从题目问题来看，题目考查运动变化过程中，变量之间的关系，如何建构函数关系式和如何抵消变量是解决本题的两个重要环节，首先需要解决构造三角形面积函数问题，再利用变量之间的关系抵消变量.

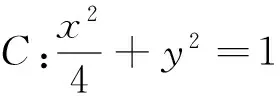
假设各个要素的构造顺序是：切点P——切线l——交点A,B——弦AB.因此可以从设圆的切线入手，其与椭圆相交成弦AB，将弦长|AB|和原点O到直线l的距离d表示为点P坐标的函数，再抵消变量得到定值.