一道全国高中数学联赛湖南赛区预赛题的探究

张 慧 于兴江

山东聊城大学数学科学学院 (252000)

圆锥曲线中的定点问题是一类非常重要的题型，近年来的高考题多次考察定点问题.基于此,笔者利用几何画板对2016年全国高中数学联赛湖南赛区预赛的第13题进行了探究.

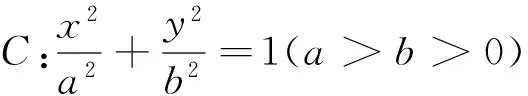
(1)求椭圆C的方程;

(2)联结AE、BD，当直线l的倾斜角变化时，直线AE与BD是否交于定点?若是，求出定点的坐标并给予证明；否则，说出理由.

根据原题给出了圆锥曲线的定点问题的几个结论.

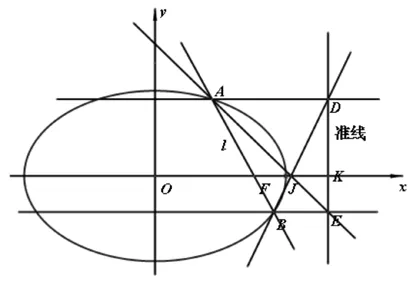
图1

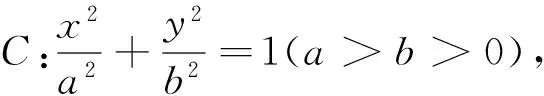
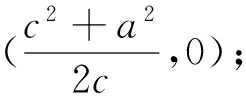
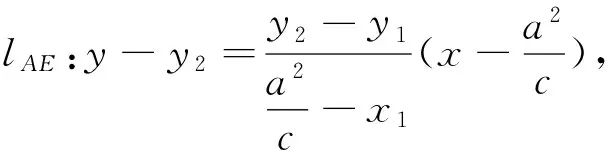
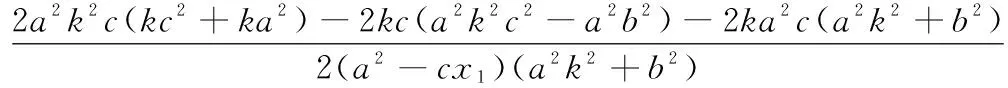
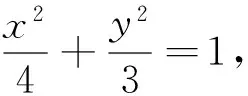
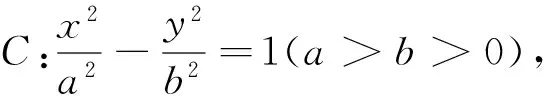
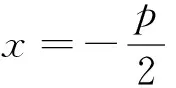
定理2、定理3的证明方法与定理1类似，不再一一赘述.

由定理1，2,3可得

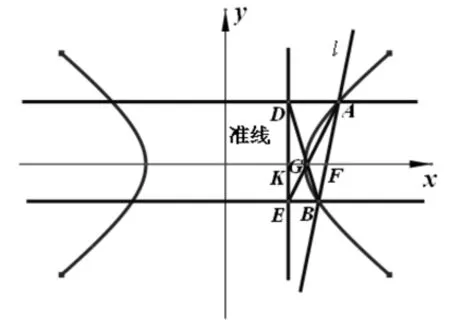
图2

定理4 设圆锥曲线C，直线l经过圆锥曲线C的(右)焦点F，与圆锥曲线C交于点A、B，点A、F、B在(右)准线上的射影依次为D、K、E.则对于任意直线l，直线AE与BD相交于线段FK的中点G.以双曲线为例，如图2所示.

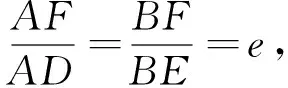
比较定理1与定理4的证明方法可以发现，定理4用几何方法证明更加简便.定理4用圆锥曲线的第二定义(平面内到定点与到定直线距离的比为常数e的点的轨迹)和初中所学的相似三角形的性质就可以证明.可见用几何方法解决这类问题较为简便，但不容易想到.

[1]2016年全国高中数学联赛湖南赛区预赛[J].中等数学(天津),2017,6.35.

[2]柳俊婷,于兴江.2015年山东理科第20题的多解分析及探究[J].中学数学研究(江西),2015,8.

[3]姜晓洁,于兴江.对2015年北京高考数学理科19题的推广研究[J].中学数学研究(江西),2016,4.