高考中三角形背景下的最值问题探究

朱建军

江苏省海门中学 (226500)

三角背景下的最值问题是高考的重点和热点之一，近几年江苏高考频繁出现此类问题.这些问题归纳起来主要有求边的最值、角的最值、面积的最值.本文通过对高考复习教学中遇到的各类三角形背景下的最值问题的研究，多角度、多渠道探究解题方法，进一步丰富学生的解题策略，进而培养学生综合分析问题的能力，形成良好的数学素养.

一、利用基本不等式求解

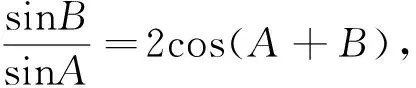
思路1：利用正余弦定理把角转化成边的关系，用基本不等式求最值.

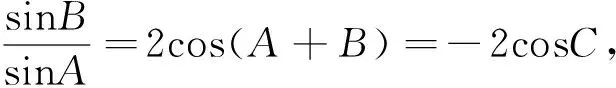
思路2：利用两角和差公式转化成角的函数，构造基本不等式求最值.

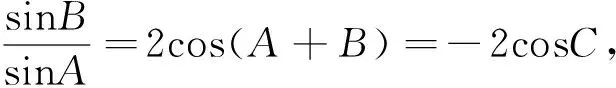
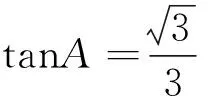
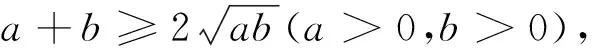
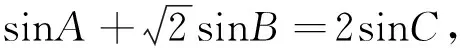
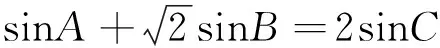
二、利用函数思想解题

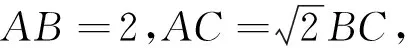
思路：求解最值问题，有时可利用函数思想，用边长或角作为自变量转化成某一变量的目标函数.

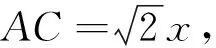
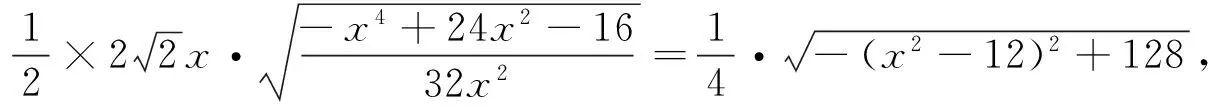
评注：求解最值问题或取值范围问题，可以尝试把所求问题转化为函数问题，利用函数求最值的方法(如配方法、导数法等)去解题.此法虽入手简单，但计算量较大，得分率不高.

三、利用解析法解题

思路：再解上题2，本题还可采取解析法，建立直角坐标系，通过曲线与方程的关系转化为阿波罗尼斯圆，进而求出高.

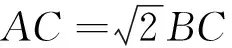
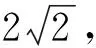
评注：此题为2008年江苏省高考填空题，实际上是用三角形作为包装条件，本质考查的是阿波罗尼斯圆的知识，此题用本文中的函数法来解，就非常复杂，而且运算量较大.阿波罗尼斯圆的知识来源于书本，由此可见书本上的习题和例题是我们上课的有效资源，应充分利用和挖掘，要让学生体会到高考试题来源于书本.

四、利用判别式法求解

题3 在ΔABC中，已知AB=2,AC2-BC2=6，则tanC的最大值是 .

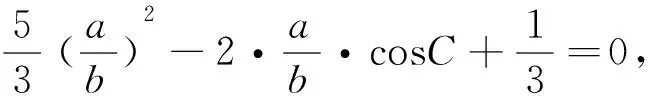
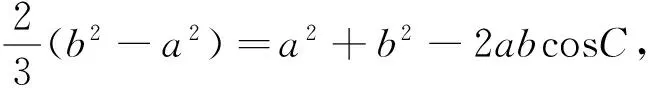
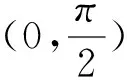
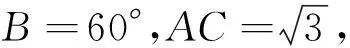
总之，三角形最值问题是高考考查的重、难点之一.高考中此类问题综合性强，解法灵活.考查注重与函数、不等式、几何等知识的融合.求解时，需要结合函数、基本不等式、正余弦定理、平面图形的几何性质等相关知识，充分运用数形结合、函数与方程等数学思想方法，实现几何问题与代数问题的有效转化.