求二元函数t=G(x,y)(F(x,y)=0)值域的本质及其意义

张玉彬

贵州省毕节市梁才学校 (551700)

已知二元方程F(x,y)=0，求二元函数t=G(x,y)的取值范围或最值问题,实质是二元函数t=G(x,y)(F(x,y)=0)的值域问题，其中F(x,y)=0叫约束条件或叫后天定义域，t=G(x,y)叫目标函数，是一类非常基础而普遍的数学问题，是高考的必考问题，这类问题的本质是求方程(组)的实解集(文[1])，这类问题最简单直接的是：已知F(x,y)=0，求G(x,y)的取值范围(最值)，如，已知正实数x,y满足x2+y2=2x，求x+y的取值范围，比较隐蔽而困难的是：根据题意列方程F(x,y)=0(约束条件)，t=G(x,y)(目标函数)，如，2017年全国高考卷Ⅲ理12(见后例2)等.

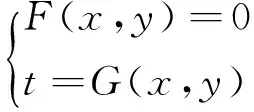
例1 已知实数x,y满足x2+y2=1，求x+y的取值范围(很能说明问题的简单例子).

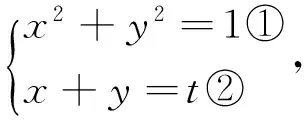
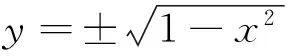
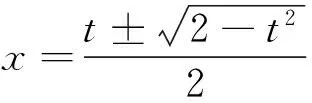
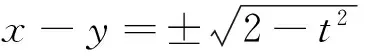
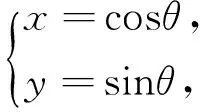
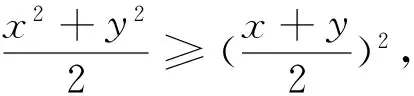
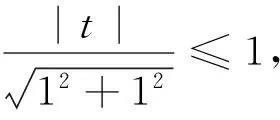
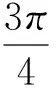
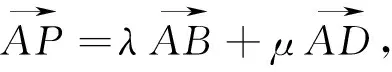
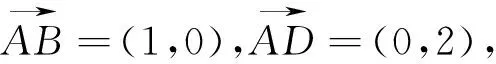
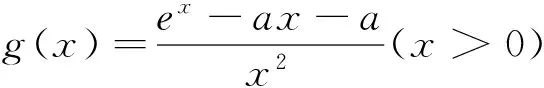
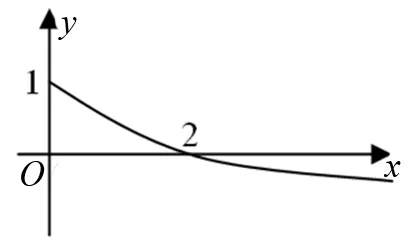
图1

解：由g′(x)=

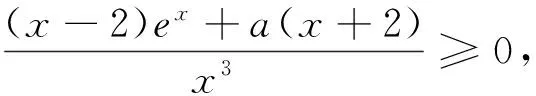
上述解法的本质是求G(x0,a)=

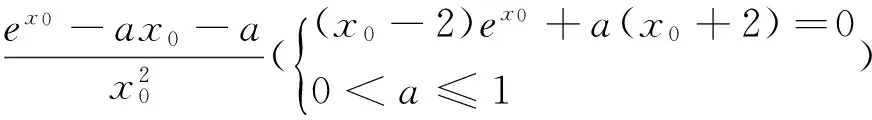
由于t=G(x,y)(F(x,y)≥0)取得最值的自变量(x,y)都在约束条件F(x,y)≥0(区域)的边界F(x,y)=0(曲线)上，所以，t=G(x,y)(F(x,y)≥0)的最值与t=G(x,y)(F(x,y)=0)的最值完全类似，就可把约束条件是不等式(组)转化为约束条件是方程来解决.

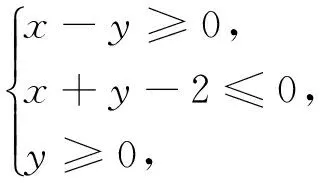
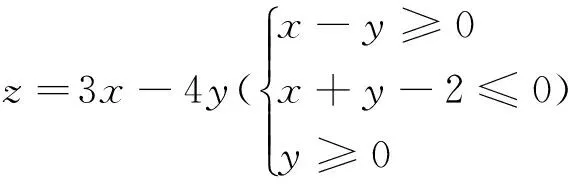
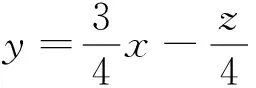
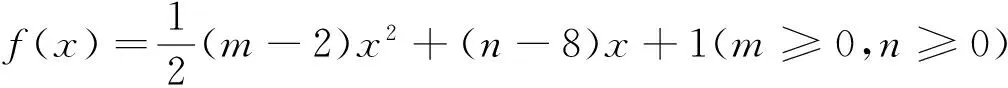
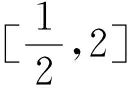
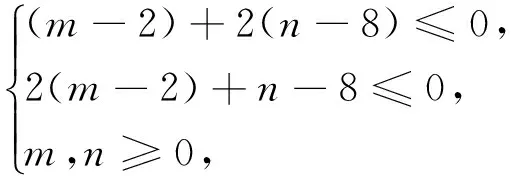
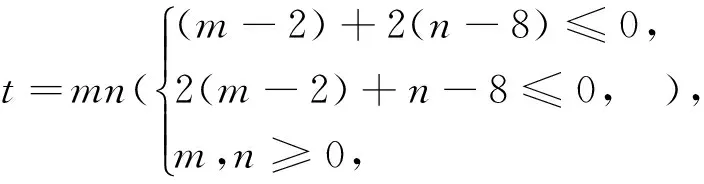
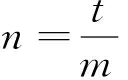
总之，求t=G(x,y)(F(x,y)=0)值域(最值)一般都有自然，简单的换，消元法和方程函数法，数学教和学都应着眼于这些方法(文[2]、文[3]).

[1]熊福州，张龙跃.数学问题的根基本质是方程的解集[J].中学数学研究(江西师大),2015,8.

[2]熊福州.换元让问题进入方程组，消元使问题在一个方程中[J].中学数学研究(江西师大),2016,12.

[3]熊福州.最基本的数学思想方法—方程思想，换(消)元法[J].河北理科教学研究，2000,4.