一道高考数列试题引发的研究性学习*
2018-05-02崔静静赵思林
崔静静 赵思林
四川师范大学数学与软件科学学院 (6100682) 四川内江师范学院数学与信息科学学院 (641112)
递推数列是刻画递推关系的数学模型,是研究离散型变量问题的重要工具,也是分形几何的基础.因此,美国的SATⅡ数学高考[1]、日本的数学高考几乎每年都有涉及递推数列的考题.数列求和方法是研究数列的核心知识,对学习大学里的《级数理论》尤其重要.高考数学全国卷比较重视对递推数列和数列求和的考查.2017年高考数学全国卷Ⅲ文科第17题是一道数列试题,该题能够激活数学思维、具有探究价值,是一道研究性学习的好问题.本文拟从试题的解题思路分析与探究、题干的递推关系的引申和第(2)问的推广等角度对这个题目做一番探究.
1.试题介绍
2017年高考数学全国卷Ⅲ文科第17题:
设数列{an}满足a1+3a2+…+(2n-1)an=2n.
(1)求{an}的通项公式;
2.试题的思路分析与探究
对于初次接触本题递推关系的考生来说,经历“观察——试算——归纳——猜想——证明——结论”过程,不难发现解题思路(结论).事实上,


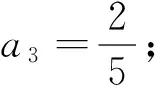

对于熟悉这类递推关系的考生来说,运用方程思想容易直接获解.
由a1+3a2+…+(2n-1)an=2n,知a1+3a2+…+(2n-1)an+(2n+1)an+1=2(n+1).

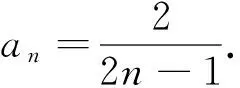

3.试题的引申与推广
引申与推广是研究数学的重要方法.引申与推广都可以将问题一般化,从而实现从“一个题”到“一类题”的跨越.引申与推广可以培养学生的问题意识、探究意识和创新意识.下面对题干的递推关系作一些引申,并对第(2)问进行推广.
观察和分析题干的递推关系,可作如下引申.
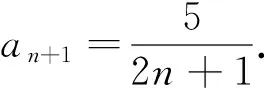
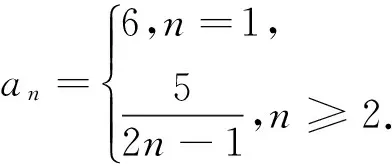
评注:引申1对原题中递推关系a1+3a2+…+(2n-1)an=2n右边的数据作了改动,这时就需要分类讨论了,显然就比原题更难了.由于本题是解答题中的第1题,命题者为了控制难度,题目中设计的数据比较特殊,考生解答题目时不必考虑分类讨论.
引申2 设a1+3a2+…+(2n-1)an=f(n),求an.


2.1.4 对疾病认识不足 患者不良心理反应的严重程度与病情轻重并不一定成正相关,这主要与患者对疾病的认识有关[5]。杨凤鸣[14]对150例 ICU 患者研究显示,60例危重症患者由于对突发的病情缺乏心理准备,认为自己病情严重会危及生命,产生十分明显的恐惧感和威胁感。
引申3 设g(n)≠0(n∈N+),g(1)a1+g(2)a2+…+g(n)an=f(n),求an.
当an≠0时,有时也把an放在分母上,见引申4,看上去就会复杂一些.

引申4的解法与引申3的解法完全相仿,此处从略.
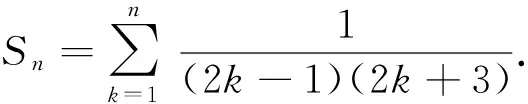


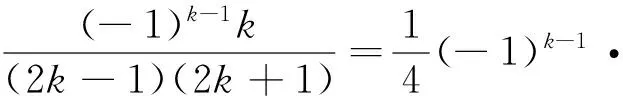



对高考试题的研究性学习,通常包括对问题结构的观察与比较,对解题思路的分析与探究,对数学问题(命题)的引申与推广,对数学方法的尝试与优化等过程.
[1][美]库(RichardKu),[美]道奇(HowardP.Dodge).BARRON’SSATⅡ数学(第9版)[M].北京:世界图书出版公司北京分公司,2011:153-160.
