在教学中引导学生学会“善学”的教学实践—以一元二次方程的解法为例

广东省中山市永宁中学(528415) 冯叶平

一元二次方程的解法一般都认为有四种,包括直接开平方法、配方法、公式法、因式分解法,而因式分解法又包含了提取公因式法、运用公式法、十字相乘法,而运用公式法又包括了运用平方差公式及运用完全平方公式.可以表示成下面的关系:

十字相乘法课本并不作要求,但由于在后续的一元二次方程的应用及二次函数的问题中,遇到的方程经常是用十字相乘法解非常容易,因此在平时的教学中,一般都补充十字相乘法解一元二次方程这内容的教学.

从上图不难看出,一元二次方程的解法细分就有常见的7种那么多,因此面对不同形式的一元二次方程,如何选择最优的方法进行解题提高运算的速度及准确性,如何理解各种解法之间的关系也存在比较大的困难.本文结合平时的教学,谈谈如何在一元二次方程的解法中引导学生学会“善学”.

1.观察比较识真面目

下面通过展示教学中的部分环节来说明我是如何引导学生进行学习,达到“善学”这目的的.

1.1 新解法引入时引导学生观察、比较

通过一元二次方程第一课时的学习,学生已经懂得运用直接开平方法进行解方程一元二次方程时,方程都可以化成这两种形式:x2=p(p≥0),(mx+n)2=p(p≥0).

第二课时教学配方法时,其中引入新课的题目设计如下:

1.解方程:(1)4x2=25;(2)2(x-1)2=4;

(3)x2+6x+9=0.

(变式)2.解方程:x2+6x+4=0.

设计意图非常明显,第1题的前两个小题为了复习直接开平方法的两种类型,第(3)题及变式就是为了引导出配方法.

在教学过程中发现,学生第1题的前两个小题很快做出来,第(3)题也有部分同学完全平方公式非常熟练能够顺利完成,但有部分同学被卡住了.这时,老师引导学生进行观察对比:

师:同学们,请大家观察第(1)、(2)题与第(3)题方程的区别?

生:前两题都是一个代数式的平方等于一个数,第(3)题不是了.

师:与我的想法一样!厉害!同学们再认真观察一下,第(3)个方程还有什么不同呢?

生1:方程右边是0.

生2:是一元二次方程的一般形式.

生3:可以写成一个代数式的完全平方.

师:大家观察非常仔细,都对!同学们生3告诉我们,可以写成一个代数式的平方,那问题解决了吗?

学生理解了第(3)题的解答.老师抓紧机会进行小结:同学们通过观察、比较就能够辨清题目之间的异同,就能够找到问题解决的办法,这种学习方法值得多使用.那么第2题呢?

师:我们继续观察这方程,看看又有什么不同?

生1:与第(3)是一样的.

师(追问):为什么说一样呢?

生1:方程右边也是0,也是一元二次方程的一般形式.

师:非常准确!这是相同的地方,能找出不同的地方吗?

生2:这个方程左边不能写出一个完全平方式了.

师:你的观察能力真强!

学生找到了方程的异同点,学习了第(3)题,这道题学生就很容易找到了解题的突破口,找到了方向.

1.2 课堂练习时引导学生观察、比较

每节课在新解法的学习完成后,必然要进行有针对性的练习,此时学生也需要观察方程的异同,选择最优的解法进行求解.特别是学生在学习利用因式分解法求解时,如果学生观察不仔细,那求解的速度及准确性将大打折扣.下面通过用因式分解中的提取公因式法解一元二次方程的巩固练习来说明:

7.解下列一元二次方程.

(1)x(x+2)-(x+2)=0;(2)x(2x-3)+5(3-2x)=0;

(3)x(x+2)=x+2;(4)3x(2x+1)=4x+2.

这是用因式分解法解一元二次方程例题学习后的课堂练习,课堂练习一般采用先练习后点评的教学方式.由于到这节课为止,课本介绍的所有解法都学习完毕,因此在设计题目的时候,并没有规定学生用什么方法进行求解.教师完全可以预计到,学生一定有各种不同的解法,教师通过展示不同的解法,让学生进行对比,从而认识到选择最合适方法达到省时、准确的效果.

教师投影学生答案进行点评:

第(1)题学生都能够用因式分解法求解;

第(2)题投影两个学生的答案,先投影错误的,然后引导学生观察比较两个方程的区别在哪里,能否化成含有公因式的方程?如何化?最后投影一个准确的答案进行强化.

第(3)题,教师先投影一个去括号后用配方法求解的答案,然后提问是否有别的解法,再投影学生的解法,让学生回答为什么能够想到用因式分解法来完成?因为含有公因式(x+2),一个在左边、一个在右边,移到左边就解决问题了.

第(4)题,公因式更加隐蔽了,因此更多的学生是采用了去括号后用配方法完成了.这时,教师提出:同学们再观察观察第(4)题,用什么方法解最快呢?这时,又有一部分学生能够识别隐蔽公因式的真面目了.

教师进行及时的追问,在解一元二次方程时,我们应该如何做:

生1:应该先观察方程,再选择方法;

生2:应该找到方程的不同的地方;

生3:应该学会比较;

生4:应该先考虑用因式分解法;

······

观察是人的一种有目的、有计划的知觉;比较是在思想上确定事物异同的思维过程.教师在同一教学时间内向学生呈现两种或多种不同的方程形式引导学生观察,求同寻异,促进和加深学生对不同类型的方程选择不同解法的认识.教师通过教学,引导与强化学生进行观察、比较,让学生在潜移默化中养成一种习惯.找到异同,其实就是找到突破口了.

2.巧用转化得真结果

数学思想方法是数学的精髓,而转化思想方法又是数学思想的核心和精髓.何为数学思想,布鲁姆在《教育目标分类学》中明确指出:数学转化思想是“把问题元素从一种形式向另一种形式转化的能力”,它可以从语言描述向图形表示转化,或从语言表达向符号形式转化.数学以其独特性,转化的思想经常用到,对于一元二次方程的解法当然也不例外.因此在教学的过程中,要让学生巧用转化的数学思想进行一元二次方程的学习.

2.1 复杂与简单之间的转化

一元二次方程相对一元一次方程来说复杂多了,在教学的过程中,通过开平方、因式分解等办法,把相对较为复杂的一元二次方程转化成了一元一次方程进行求解,体现了复杂与简单之间的转化.在高次方程、多元方程组等初中的代数中经常使用这种方法.学生理解了这种方法,懂得迁移运用了,对于高中学习一元二次不等式就更容易理解.

2.2 已知与未知之间的转化

这在数学学习中太常见了,以前面提到的方程为例进行说明.

1.解方程:(1)4x2=25;(2)2(x-1)2=4;

(3)x2+6x+9=0.

(变式)2.解方程:x2+6x+4=0.

学生已经观察、对比出上面方程之间的差别的,因此引导如何把第(3)题转化成第(1)、(2)题的形式,问题就解决了.

第(3)题解决了,把9变成4,又应该如何做呢?学生也自然想到了化成完全平方式.

用配方法解二次项系数不是1的一元二次方程时,学生通过观察、比较,也非常容易想到应该利用等式的性质把二次项系数化1,从而把未知的转化成已知的.

2.3 一般与特殊之间的转化

在一元二次方程中,如果方程具备“ax2+bx=0(a/=0)”这种形式时,均可用因式分解法中的提取公因式法解一元二次方程.但是“ax2+bx=0(a/=0)”中的“x”,既可以代表单项式,也可以代表多项式,方程也不一定是右边等于0的形式,因此,在教学的过程中,引导学生认准这种类型的特征:含有因式、方程可以看成由两大项组成,学生就比较容易把(2)、(3)、(4)这种特殊的方程转化成一般的熟悉的(1)的形式进行解答了.

7.解下列一元二次方程.

3.自我效能感促成功

数学知识是一环紧扣一环,螺旋上升的.在教学中如果能够根据这特点进行教学,学生不但明白了知识与知识之间的关系,学生的知识体系也构建起来了,学习起来更加轻松.一元二次方程的学习同样具有这特点,教学中让学生明白,本节课相对以前知识只是多了一步或者两步的解答过程,学生感觉可以接受,学起来就有信心了.下面举例说明:

1.在直接开平方法中:

从解答过程的比较中让学生发现,本节课相对以前的内容只是多了答题这一步,学生感觉我要学会本节课内容的心理距离就非常小了,自我效能感就高,学起来就有信心了.

2.在配方法中:

从对比中不难发现,配方法只是比直接开平方法多了两步而已,而移项非常简单,对于配方这一步,用以下四道练习进行寻找规律与巩固,学生发现这节课最难的地方居然自己也轻松掌握了,自我效能感自然也特高.

①x2+12x+___=(x+___)2;

②x2-10x+____=(x-____)2;

③x2-x+___=(x-___)2;

④x2+3x+____=(x+____)2.

对于二次项系数不是1时,如2x2-3x+1=0,只需要利用等式的性质把二次项系数化1,转化成已知的方程就可求解了,发现也不难,只是在运算的过程中出现了分数.

为了了解教学效果,我找了一个班级进行对比,以下数据是初二年级下学期期末考试两个班级的学生数学成绩的分析,可以发现实验班的成绩明显低于对比班的成绩(见下图表1—表3).

表1 单个样本统计量

表2 单个样本检验

表3 相关性

在一元二次方程的单元测验中,解法占30分,我再次统计两个班解法这部分的分数,并进行分析,可以看出实验班在这次测验中,已经超越对比班,取得了可喜的成绩(见下图表4—表6).

表4 单个样本统计量

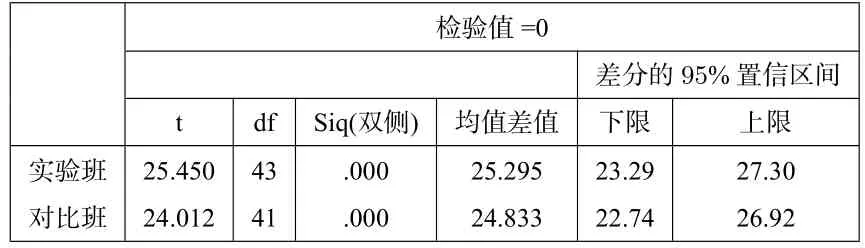
表5 单个样本检验

表6 相关性

结合测验数据分析,回顾一元二次方程解法的教学过程,感觉大部分学生学都掌握了一元二次方程的解法,学生的学习效果比较明显,达到了“善学”的目标:通过教学,引导学生学会了观察、学会了比较,能够把转化的思想、整体的思想运用到学习中;通过教学,帮助学生了解知识间的关系,对学生构建知识体系、融会贯通的运用知识解决问题起到重要的作用;通过解法过程的观察与对比,学生能够每节课突破难点,增强了学生的自我效能感.班杜拉等人的研究表明,个体的自我效能感对其行为的坚持性、遇到困难时的态度以及活动时的情绪状态都有影响.我们有理由相信,学生将会越学学有兴趣,也会越学学会学!

[1]义务教育教科书九年级数学上册(2014年3月第1版)[M].人民教育出版社.1-14.

[2]林清.浅谈转化思想方法在高中数学解题中的应用[J].福建教育学院学报,2008(12).92.

[3]“中国学生发展核心素养”出炉[EB/OL].[2016-9-20].http://news.jyb.cn/china/gnxw/201609/t20160920_674241.html

[4]浅谈小学数学教学中的比较教学法[J].中小学教师培训,1995(X2).

[5]全国统一(联合)考试大纲及指南(教育学、心理学)(2003年4月第5版)[M].北京师范大学出版社.