基于Matlab的悬架系统运动校核研究

王 伟，潘 丽 Wang Wei，Pan Li



基于Matlab的悬架系统运动校核研究

王 伟1，潘 丽2Wang Wei1，Pan Li2

（1. 中国第一汽车集团公司技术中心 轻型车部底盘设计室，吉林 长春 130011； 2. 中国工商银行康平街支行，吉林 长春 130011）

依据板簧自身特性，建立板簧弧高与板簧卷耳中心距变化关系的骨架模型，利用Matlab将该骨架模型进行程序化表示并实例分析。基于骨架模型开发悬架系统运动校核界面化程序，以某轻型货车前悬架匹配为例，利用该程序进行板簧、吊耳、减振器、稳定杆的运动校核，并利用SAE标准方法对校核结果进行校验，结果表明基于Matlab的悬架系统运动校核对提高悬架系统开发和平台匹配设计的效率具有重要意义。

Matlab；板簧悬架系统；骨架模型；运动校核

0 引 言

悬架系统一般包括弹性元件、减振器、稳定杆等零部件，运动校核是悬架系统设计流程中不可缺少的一部分，板簧式悬架系统运动校核主要涉及吊耳摆角、减振器行程、吊臂摆角、稳定杆与吊臂的夹角等[1]。采用的校核方法大多是在AutoCAD中进行二维布置校核或借助三维软件如Pro/E、UG等进行校核[2]，需要进行图纸绘制、建模等工作，实用性差、效率低。依据板簧自身特性，提出一种基于Matlab的悬架系统运动校核方法，开发用户界面，通过相关设计参数输入进行悬架系统相关校核，与传统方法相比，具有准确性高、效率高等优点。

1 悬架系统简化模型

商用汽车通常采用板簧弹簧式悬架系统，某轻型载货汽车的前悬架系统结构如图1所示，主要包括纵置式钢板弹簧、吊耳、减振器、稳定杆、吊臂、U形螺栓、固定支架及连接销等。

当车轮受载上、下跳动时，随着轴荷的变化及工况的不同，板簧簧片本身会发生弯曲变形，板簧两端卷耳中心的距离随之变化，由于前卷耳只能绕板簧前支架销轴转动，所以板簧两端卷耳中心距的变化只能由可以绕板簧后支架销轴转动的吊耳的角度变化来补偿，同时减振器、稳定杆、吊臂也会随着板簧的弯曲表现发生相对运动。

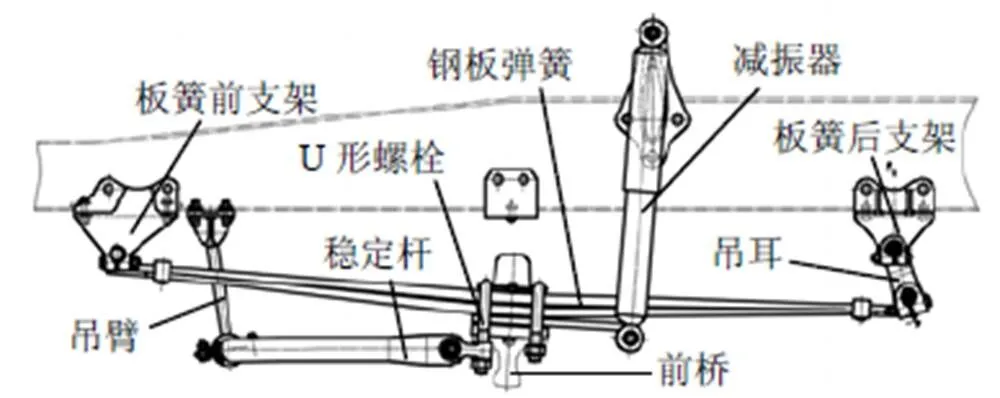
图1 前悬架系统结构

在整个悬架系统运动变化过程中，板簧各簧片的长度可以近似认为是没有变化的[3]，簧片在自由状态下是一段圆弧，由于两个U形螺栓装配预紧力的作用，使簧片中间部分出现一平直段（有些簧片可以在制造过程中就把中部做成平直段），所有簧片本身可以认为是由两段圆弧和中部直线段构成，图1简化后的模型如图2所示。

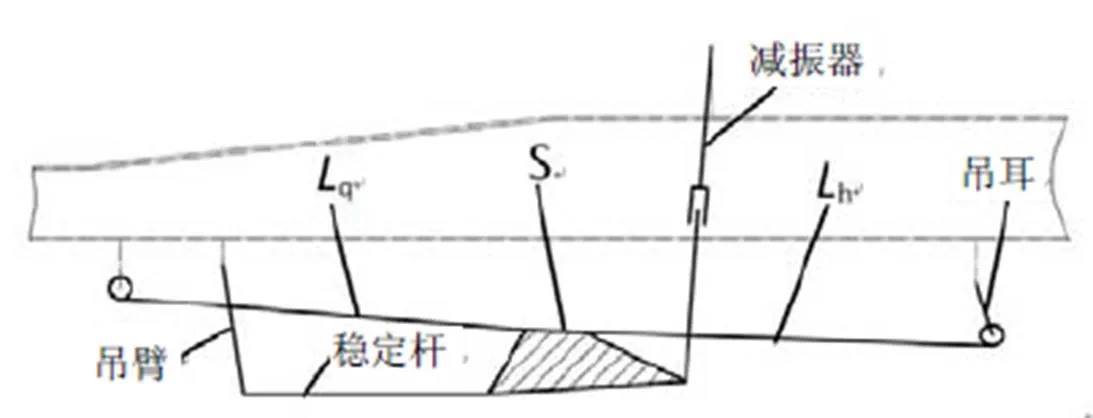
图2 前悬架系统简化模型

板簧作用长度可以表示为

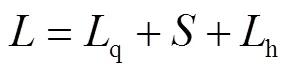
式中，为板簧作用长度，即板簧伸直后前、后两卷耳中心之间的距离；为板簧平直段，即板簧夹紧距；q、h分别为板簧前、后段圆弧，当板簧采用对称式布置时，q=h=(-)/2。

2 板簧骨架模型

板簧工作状态包括常规状态、反弓状态和S变形状态等。常规状态指载荷在设计范围内，板簧的变形基本上处于前、后卷耳根部连线以下部分；反弓状态指随着载荷增加，板簧的变形处于前、后卷耳根部连线以上部分（瞬时的冲击载荷也会造成板簧反弓）；S变形状态指当汽车紧急制动时，在车轮制动力和整车惯性力的共同作用下，板簧会出现前低后高S变形状态。无论哪种工作状态都伴随着板簧弧高的变化，因此，建立板簧弧高与板簧两端卷耳中心距的关系对悬架系统运动校核具有重要作用。

2.1 板簧骨架模型关系式

对于板簧这种零部件，在受力弯曲变形过程中，一侧材料受拉长度增加，另一侧材料受压长度缩短，只有中间的一层材料长度没有发生变化，也就是通常说的中性层，板簧作用长度其实就是中性层的长度。无论是对称式或非对称式板簧，前、后段变形原理一致，利用弦长分析法建立半段板簧模型，如图3所示。

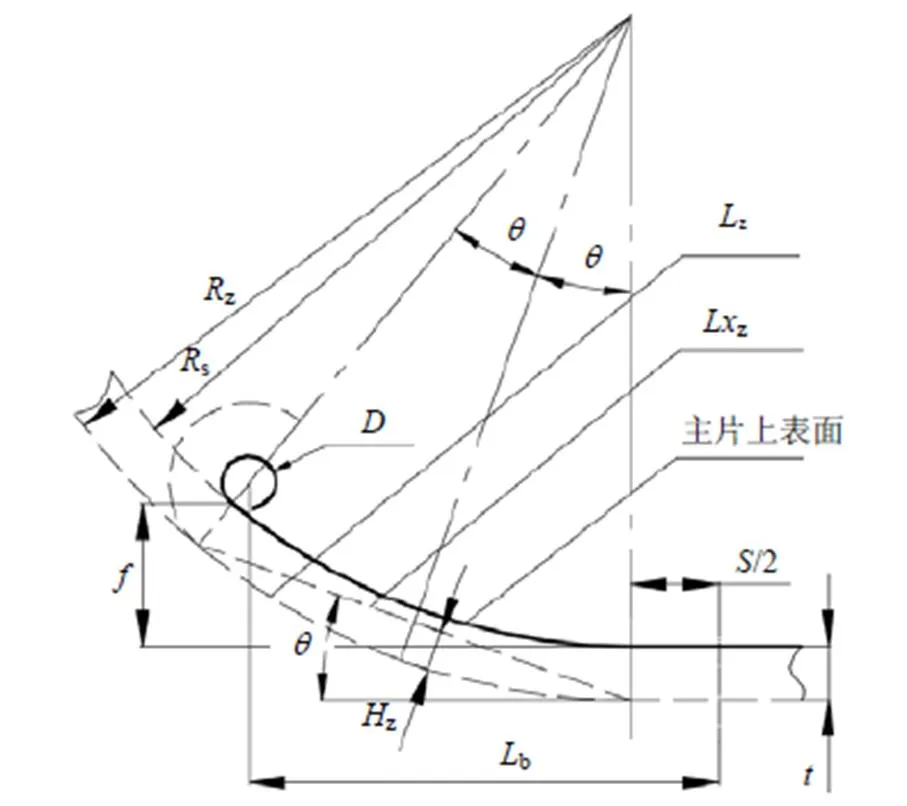
图3 前段板簧模型

由图3得如下各关系式。

式中，z为板簧前段圆弧中性面的曲率半径；s为板簧前段圆弧上表面的曲率半径；z为板簧前段弧长；z为前段圆弧中性面对应的弦长；z为中性面对应的拱高；为板簧弧高，即板簧上表面与两端（不包括卷耳孔半径）连线间的高度差[3]；为板簧簧片厚度；为板簧卷耳孔内径；b为板簧前卷耳中心至中轴线的距离；为弦切角。

从式（2）可知，当z为定值时，z、z、b都是的函数，改变值，z、z、b都会相应有唯一值对应。对于给定的板簧，z一般均为已知，可以通过改变建立板簧各种工作状态下与b的关系式，进而得到板簧弧高与板簧前、后卷耳中心距的关系，确定板簧的骨架模型。

为了便于计算，利用Matlab软件编写板簧骨架模型函数math_air，其表达式为[_，_]=math_air（z，，，，，），如图4所示。

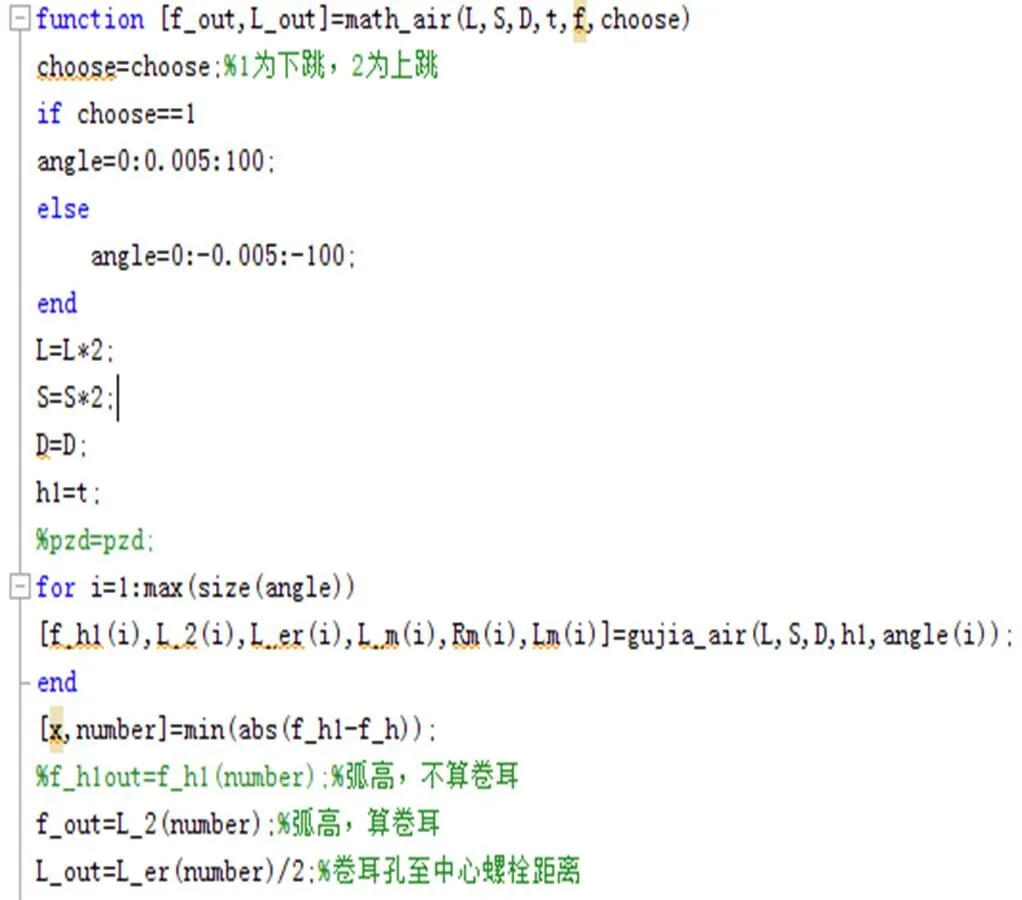
图4 骨架模型函数math_air

图4所示函数中，输出项为_和_，前者为板簧前、后卷耳中心连线至板簧主片上表面的距离，一般对现有板簧来说，这个数值可以直观测量；后者为板簧前、后卷耳中心连线的距离。对于变量，当=1时，板簧为常规状态，包括平直状态；当=2时，板簧为反弓状态。

2.2 骨架模型实例分析

某轻型车用对称式板簧如图5所示，板簧总成簧片数为3，作用长度1 280 mm，片宽70 mm，中间平直段120 mm，弧高75 mm。各簧片中部厚度15 mm，第一簧片卷耳孔径30.5 mm，端部厚度9 mm，其余簧片端部厚度 8.5 mm。

图5 某轻型车用对称式板簧

利用math_air函数对图5所示板簧骨架模型进行模拟计算，输入输出结果见表1，其中取值为2，0，1。

表1 板簧骨架模型模拟计算

（b）输出变量 mm

为了验证函数math_air对板簧骨架模型模拟的准确性，利用试验设备对图5板簧进行装配，如图6所示。

图6 板簧试验装配

图6采用液压缸对板簧进行加载，初始位置为板簧自由状态，每次液压缸给进量为5 mm，测量板簧相关数值，输入输出结果见表2。

表2 板簧试验计算

（b）输出变量 mm

表1和表2中_与_的关系曲线如图7所示。

图7 结果对比

从图7可以看出，试验曲线与模拟曲线一致性较好。

3 悬架系统运动校核

3.1 Matlab界面化程序运动校核

基于板簧骨架模型，利用Matlab对图1所示的汽车前悬架进行系统化编程，输入、输出界面如图8所示[4]。

图8 运动校核程序界面

界面包括计算参数、前悬架简化模型、校核结果输出等，某轻型载货汽车前悬架系统的具体参数输入见表3。

表3 某轻型载货汽车前悬架系统输入参数

续表3

在进行悬架系统全新开发或平台车型匹配设计时，可以依照整车给定的满载轴荷、整车姿态、偏频及布置空间等要求初步给定表3中的参数。依据表3中参数进行AutoCAD二维布置校核或三维模型校核；如果校核结果不满足设计要求，需要对表3中的参数进行调整，再重新校核，直至满足设计要求为止。

利用图8程序对表3中的参数进行匹配计算，校核结果见表4。

从表4可以看出，吊环摆角、稳定杆与吊臂夹角的变化范围符合设计要求；针对减振器行程范围，首先查看现有产品是否符合该行程范围，如果没有，那么在满足减振器自身尺寸设计要求的前提下，依据该行程范围进行开发。

3.2 基于SAE标准方法的校验

SAE标准方法已得到业界的广泛认可，指出由于板簧具有变形能力，车轮的上下运动不是绕板簧前轴销旋转的圆周运动，其实际运动轨迹接近一段圆弧，取决于板簧主片中心的轨迹。根据试验研究，板簧主片中心的摆动中心相对前卷耳中心的水平距离为2=（q+h）/8，高度距离为3=/4，摆动半径1理论上为一定值[5]。针对表3参数，图8界面化程序已给出参数输出，即2=149.05 mm，3=7.625 mm，1= 491.59 mm。

将SAE标准方法中的摆动中心添加到基于板簧骨架模型的悬架系统运动校核中，悬架系统弧高从上跳极限67 mm至下跳极限95 mm范围内调整时，得到板簧主片中心距该摆动中心距离2。1与2的对比关系见表5。

从表5对比数据可以看出，板簧从上跳极限至下跳极限整个变化过程中，最大误差绝对值不超过0.2%，验证了校核方法的可行性和校核结果的准确性。

4 结束语

利用Matlab建立板簧弧高与板簧卷耳中心距的骨架模型函数，并通过某轻型车用板簧实例对骨架模型函数进行准确性分析；基于骨架模型函数开发板簧悬架系统运动校核界面化程序，并对某轻型车前悬架进行运动校核分析，校核结果不仅满足SAE标准方法的要求，而且更直观，效率更高，对悬架系统开发、平台匹配设计具有实际意义。

[1]陈家瑞. 汽车构造[M]．北京：人民交通出版社，2002.

[2]卜凡龙. 基于Pro /E 的悬架运动校核方法研究[J]．汽车零部件，2015(8)：31-35.

[3]王望予. 汽车设计. 第4版[M]. 北京：机械工业出版社，2011.

[4]苏金明，阮沈勇. Matlab实用教程[M]. 北京：电子工业出版社，2005.

[5]田其铸. 汽车设计手册[Z]. 长春：长春汽车研究所，1998.

2017-11-13

U463.33

A

10.14175/j.issn.1002-4581.2018.02.001

1002-4581（2018）02-0001-05