基于非局部平均的SAR图像相干斑抑制算法

2018-04-28刘珂良

西安工程大学学报 2018年2期

胡晓,朱磊,崔琳,潘杨,刘珂良

(西安工程大学电子信息学院,陕西西安 710048)

0 引言

图像去噪一直是图像处理领域的经典研究课题[1],而相干斑是合成孔径雷达(SAR,synthetic aperture radar)对分布式目标作相干处理后在图像上形成的乘性噪声[2]．相干斑噪声的存在降低了系统对目标的分辨能力,使得SAR图像的特征检测、图像分割和目标分类等解译工作复杂化,因此,抑制相干斑噪声一直是SAR图像处理的重要步骤[3]．

SAR图像相干斑抑制主要有两大目标:一是消除图像中均匀平坦区域的乘性噪声;二是尽量保留原有图像中的边缘、纹理等结构信息．近几十年来,国内外学者为了同时满足这两大目标,提出了许多经典的SAR图像降斑技术．早期对相干斑噪声进行处理的多视处理技术[4],因其大大降低图像的分辨率而渐渐被淘汰,人们开始更多地研究滤波后处理技术消除斑点噪声,大致分为3类:空域滤波[5-7]、各向异性扩散滤波[8-10]和变换域滤波[11-13]．空域滤波是最早采用并广泛用于相干斑的抑制技术,以Lee滤波[5]、Kuan滤波、Frost滤波[6]和其改进[7]为代表,该类算法采用滑动窗口技术估计窗内局部统计特征自适应地进行平滑滤波,由于其仅仅考虑了局部邻域特征而忽略图像结构信息,无法同时兼顾抑斑性能和边缘保护．为了克服此缺陷,Buades等[14]于2005年提出针对自然图像加性白噪声的非局部均值(NLM，non-local means)算法．该算法采用图像的块相似性替代传统的单像素点相似性来构造权重,从而可以更好地保护边缘和纹理等特征；文献[15-18]将非局部平均技术运用于SAR图像的相干斑抑制中,取得了不错的效果；Chen等[16]提出的NL-CV算法,既保护了图像边缘又抑制了相干斑,但高灰度值同质区残留噪声严重；刘书君等[17]提出基于非局部分类处理的SAR图像降斑方法,首先将图像分为同质区和异质区,然后分别采用加权平均和3D变换域硬阈值收缩方法进行去噪,达到了较好的抑斑性能和视觉效果；陈世媛等[18]设计了基于Gabor滤波器的自适应均值算法,不仅有效去除了相干斑噪声,而且很好保护了纹理和边缘信息．

针对高灰度值同质区残留噪声严重这一缺陷,文中给出一种基于非局部平均的SAR图像相干斑抑制算法.由于乘性噪声使图像的高灰度值同质区起伏较大,因此文中对原始SAR图像进行对数变换和高斯平滑,加快了高灰度值同质区的衰减速度,然后再计算高斯加权欧式距离作为相似性测量参量;以可分辨原始SAR图像平坦区与边缘区的变差系数(CV,coefficient variation)的倒数作为自适应衰减因子,较好地保护了边缘;联合新的相似性测量参量和自适应衰减因子构造新的加权系数对图像整体信息进行加权平均滤波．实验结果显示,该算法抑斑的图像视觉效果更清晰,高灰度值同质区降噪性能和边缘保护方面都有较大的提高．

1 经典NLM滤波

假设一幅含噪数字图像表示为V={V(i)|i∈I},矩阵I表示图像的坐标范围,对某一像素,估计值NL[V](i)为整个图像采用非局部平均滤波后所有像素的加权平均,为

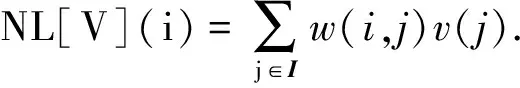
(1)

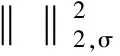
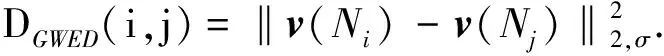
(2)

与v(Ni)有相似灰度值的所有邻域像素在加权平均时被分配较大的权重,权重定义为

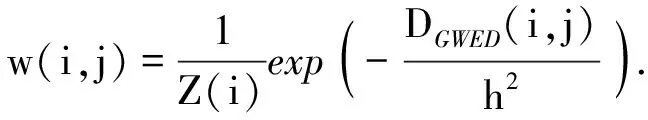
(3)

式中:参数h为衰减因子,代表了滤波器的滤波程度;Z(i)是归一化常数,有

(4)

由于SAR图像相干斑是乘性噪声,经典NLM方法不能用于SAR图像去噪,文献[16]结合SAR图像特点提出NL-CV滤波算法,用变差系数CV代替经典NLM算法中的衰减常数,既保护了图像边缘也抑制了相干斑,但高灰度值同质区残留噪声明显．为了解决高灰度值同质区去噪困难这一难题,文中给出一种基于非局部平均的SAR图像相干斑抑制算法．

2 相干斑抑制算法

首先对SAR图像进行对数变换和高斯平滑处理,然后计算处理后图像的高斯加权欧氏距离作为相似性测量参量,再以可分辨原始SAR图像起伏程度的CV的倒数作为自适应衰减因子,结合新相似性测量参量和自适应衰减因子求得新权重,最后利用新权重对原始SAR图像进行非局部加权滤波．

2.1 相似性测量参量估计

由于SAR图像固有的噪声是乘性噪声,设一幅SAR图像在位置i处的观测值为Y(i),有用回波信号为X(i),相干斑噪声为S(i),得

Y(i)=X(i)S(i).

(5)

而经典的NLM算法是针对加性高斯白噪声的,因此需首先对服从Gamma分布的乘性噪声取对数处理,将乘性噪声转化为加性噪声,噪声分布近似高斯分布[19],得

logaY(i)=logaX(i)+logaS(i).

(6)

式中：a是底数,此处底数a取10.然后将得到的图像通过高斯滤波器进一步消除部分噪声,此时得到的图像用Gδ{logaY(i)}表示,那么像素i和像素j的相似性用高斯加权欧氏距离可表示为

(7)

图1是本文算法与文献[16]提出的NL-CV滤波算法对简单仿真图的相似性测量比较．

(a) 仿真SAR图像 (b) 本文算法

图1(b)和图1(c)分别是图1(a)的A～D窗用本文算法与NL-CV算法的相似性测量比较．由于经典NLM算法采用负指数加权,因此搜索窗内像素与中心像素相似程度越高,则其获得的权重就越大．图1(a)中,A、B两窗的中心像素正好在边缘线上,所以只有边缘附近像素与中心像素最相似,则边缘附近像素权重较大从而保护了边缘.从图1(b)和(c)看出,对数变换和高斯平滑后边缘附近的测量值不但明显低于两侧同质区且两侧同质区相对平滑,可以清晰地区分边缘和非边缘,而之前边缘两侧同质区起伏较大,灰度值与边缘区较为接近,对边缘保护不利.C、D窗的中心像素分别在高、低灰度同质区,比较图1(b)C窗、D窗和图1(c)C窗、D窗看出,NL-CV算法C窗的测量值明显比D窗的高,因此高灰度值同质区去噪不彻底,而本文算法在两个搜索窗内像素的测量值趋于相近,从而保证了不同区域相近的去噪效果．

2.2 基于CV构建自适应衰减因子

传统NLM算法对图像进行降噪时,采用常数h来控制图像的滤波程度,当h较小时,图像滤波程度较小,残留噪声严重;当h较大时,图像滤波程度较大,容易造成纹理细节丢失,存在很大的缺陷．CV在空域滤波中可以较好的区分边缘区和同质区,因此文中采用CV替代常数h从而自适应地在不同区域控制图像的滤波程度．仿真SAR图像对应的CV图像如图2所示．

图 2 图1(a)的CV图像Fig.2 The coefficient variation image of Fig.1(a)

由于CV的边缘区呈现高灰度而同质区呈现低灰度这一特性,文中定义新的衰减因子为

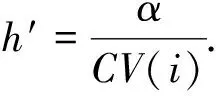
(8)

式中：α为衰减常数,可调节整个算法的滤波强度；CV(i)为方形邻域内观测值的标准差与均值的比值.

2.3 构建新加权系数及NLM滤波

由新的高斯加权欧式距离与式(8)构建的自适应衰减因子,组成本文改进算法的加权系数为

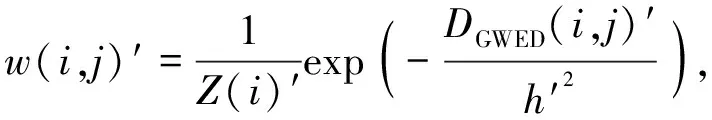
(9)

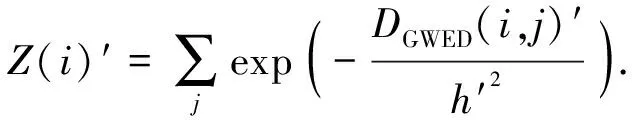
(10)

所以文中改进的NLM加权滤波可以表示为

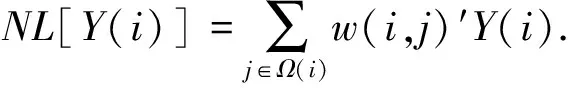
(11)

图3是经对数变换和高斯平滑前后仿真图像的边缘保护情况,明显看出,经对数变换和高斯平滑后，图3(b)边缘附近像素权值较大而边缘两侧同质区权值较小,从而更有利于保护边缘．

(a) 变换前 (b) 变换后图 3 图1(a)A窗与B窗经对数变换和高斯平滑前后的加权系数对比Fig.3 The weighting coefficient contrast of figure 1 (a) before and after the logarithmic transformation and Gaussian smoothing

2.4 算法流程

对于任意像素点i,选取以像素i为中心的搜索窗像素集合Ω(i),本文算法的具体步骤如下:

(1) 从Ω(i)内选取以中心像素i与其他像素j为中心的小尺度相似窗像素集合Y(i)和Y(j);

(2) 依照式(6)和(7),计算Ω(i)内像素i和像素j的相似性测量值DGWED(i,j)′;

(3) 计算Ω(i)内每个像素的变差系数并依照式(8)估计衰减因子h′;

(4) 依照式(9)计算Ω(i)内每个像素的加权系数;

(5) 计算Ω(i)内各像素灰度值和对应加权系数的加权平均值,并作为像素i的滤波估计值.

最后,对整幅图像的所有像素按上述5个步骤进行滤波,得到滤波后的SAR图像．

2.5 算法时间复杂度分析

由于非局部平均比局部平均算法计算量大,文中针对某一个像素点进行时间复杂度分析．设某一像素点k,其搜索窗尺度为m1×m2,相似窗尺度为n1×n2,则在像素点k的搜索窗内,在相似性测量部分,由式(6)大约需要n1×n2次乘法,由式(7)大约需要2×n1×n2次乘法和2×n1×n2次加法;计算自适应衰减因子部分,由式(8)大约需要n1×n2次乘法;在加权平均部分,由式(9)和(10)大概需要2×n1×n2次乘法,加权滤波时,由式(11)需要2×n1×n2次乘法和n1×n2次加法．总体来说,本文算法大约需要8×n1×n2次乘法和3×n1×n2次加法,与NL-CV算法的时间复杂度基本相似．

3 实验结果

为了客观评价本文算法的有效性和稳定性,对图4所示的仿真图像和真实图像分别用本文算法、经典Frost滤波[6]和NL-CV滤波[16]进行降噪处理,并从视觉效果和参数性能2个方面来判别抑斑性能的优劣．视觉效果包括去噪图像和其Canny边缘检测图像,实验结果如图5，6所示．抑斑参数性能采用了文献[9]中的方法:等效视数(ENL,equivalent number of looks)和边缘保持指数(EPI,edge preservation index)．ENL表示相干斑的平滑能力,其值越大表明相干斑抑制程度越高,本文2次实验选取的同质区为图4中的黑色方框;EPI表明图像边缘的保护能力,其值越大表明抑斑后图像的边缘保护程度越高,理想值为1．不同图像的EPI和不同区域的ENL如表1所示,并对最好的性能指标进行了字体加粗．

(a) 3视仿真SAR图像 (b) 5视真实SAR图像图 4 实验所用SAR图像Fig.4 Two SAR images for experiment

本文用各算法对2幅图像进行抑斑时,分别采取了各自最好的抑斑性能参数．各算法对图4(a)采取的参数如下:FROST算法的加权窗尺度为15×15,局部统计量估计窗尺度为7×7,衰减常数为0.5;NL-CV算法搜索窗尺度为21×21,相似窗尺度为7×7,衰减常数为300,高斯核标准差为8;本文算法搜索窗尺度为21×21,相似窗尺度为7×7,衰减常数为0.25;Canny算子的边缘检测阈值为0.07．各算法对图4(b)抑斑时采用的与图4(a)不同的参数如下:FROST算法衰减常数为2;NL-CV算法衰减常数为100;本文算法衰减常数为0.06,Canny算子的边缘检测阈值为0.06．

FROST NL-CV 本文算法(a) 去噪图像

FROST NL-CV 本文算法(b) 边缘检测图像图 5 仿真SAR图像实验结果Fig.5 Experimental results for synthetic SAR image

FROST NL-CV 本文算法(a) 去噪图像

FROST NL-CV 本文算法(b) 边缘检测图像图 6 真实SAR图像实验结果Fig.6 Experimental results for real SAR image

对比图5(a)与图6(a)可以发现，FROST滤波的图像存在模糊,NL-CV算法的抑斑图像高低灰度同质区残留噪声相差较大,而本文算法的抑斑图像比较清晰,高低灰度值同质区的相干斑噪声得到了较好地抑制．对比图5(b)与图6(b)的边缘检测图像可知，FROST和NL-CV算法的边缘检测图像在高灰度同质区存在较多的虚假边缘,而本文算法的边缘检测图像边缘相对自然平滑,高灰度同质区的虚假边缘少．

表 1 各算法对2幅SAR图像抑斑参数性能对比Table 1 Despeckling parameters contrast of each algorithm for two SAR images

由表1所示的各算法对2幅图像的抑斑性能参数比较可以看出，本文改进算法在高灰度值同质区ENL和EPI指数两个方面均优于其他2种算法,而FROST和NL-CV算法在低灰度同质区的ENL指标更好．FROST滤波因只有局部像素参与运算而抑斑性能较差,NL-CV算法虽采用了非局部思想,但由于乘性噪声的特殊性使得高灰度值同质区残留噪声严重,本文算法不仅遵循了非局部思想,而且在相似性测量时通过对数处理和高斯平滑,有效抑制了高灰度值同质区的噪声．由于本文算法在相似性测量时对图像作对数变换处理,在一定程度上影响了低灰度值区域的抑斑性能,因为SAR图像相干斑是乘性噪声,高灰度值同质区的起伏比低灰度值同质区大,而其他2种算法在低灰度值区域抑制效果很好,因此加大高灰度值区域的噪声抑制是非常有必要的．

4 结束语

针对SAR图像的乘性相干斑抑制问题,给出了一种基于非局部平均的SAR图像滤波算法．该算法首先对原始SAR图像作对数变换和高斯平滑处理,以加快高灰度区域的衰减速度从而提高了高灰度同质区的抑斑性能,然后计算处理后图像每个像素的相似性测量参量．与此同时,采用能较好检测图像起伏的CV作为自适应衰减因子,从而不影响抑斑性能的同时保护了边缘．以上两个步骤使得本文算法的抑斑图像清晰,提高了高灰度值同质区的相干斑抑制能力和边缘保护性能．

参考文献(References)：

[1] 杨国梁,雷松泽.基于贝叶斯估计自适应软硬折衷阈值 Curvelet 图像去噪技术[J].西安工程大学学报,2011,25(6):857-861.

YANG G L,LEI S Z.The image denoising method of soft and hard adaptive thresholding based on Curvelet transform and Bayesian estimation[J].Journal of Xi′an Polytechnic University,2011,25(6):857-861.

[2] WANG Y,AINSWORTH T L,LEE J.On characterizing high-resolution SAR imagery using kernel-based mixture speckle models[J].IEEE Geoscience and Remote Sensing Letters,2015,12(5):968-972.

[3] GAO F,XUE X,SUN J,et al.A SAR image despeckling method based on two-dimensional S transform shrinkage[J].IEEE Transactions on Geoscience & Remote Sensing,2016,54(5):3025-3034.

[4] OLIVER C,QUEGAN S.Understanding synthetic aperture radar images[M].Boston:Artech House,2009.

[5] LEE J S.Digital image enhancement and noise filtering by use of local statistics[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2009,PAMI-2(2):165-168.

[6] FROST V S,STILES J A,SHANMUGAN K S,et al.A model for radar images and its application to adaptive digital filtering of multiplicative noise[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,1982,4(2):157-165.

[7] 朱磊,水鹏朗,程冬.基于混合迭代滤波的SAR图像相干斑抑制[J].电子与信息学报,2012,34(5):1038-1044.

ZHU L,SHUI P L,CHENG D.SAR image despeckling based on mixed iteration filtering[J].Journal of Electronics & Information Technology,2012(5):1038-1044.

[8] YU Y,ACTION S T.Speckle reducing anisotropic diffusion[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2002,11(11):1260-1270.

[9] ZHU L,ZHAO X T,GU M H.SAR image despeckling using improved detail-preserving anisotropic diffusion[J].Electronics Letters,2014,50(15):1092-1093.

[10] 朱磊,韩天琪,水鹏朗,等.一种抑制合成孔径雷达图像相干斑的各向异性扩散滤波方法[J].物理学报,2014,63(17):445-455.

ZHU L,HAN T Q,SHUI P L,et al.An anisotropic diffusion filtering method for speckle reduction of synthetic aperture radar images[J].Acta Physica Sinica,2014,63(17):445-455.

[11] LI H C,HONG W,WU Y R,et al.Bayesian wavelet shrinkage with heterogeneity-adaptive threshold for SAR image despeckling based on generalized gamma distribution[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(4):2388-2402.

[12] ARGENTI F,BIANCHI T,LAPINI A,et al.Fast MAP despeckling based on Laplacian—Gaussian modeling of wavelet coefficients[J].IEEE Geoscience & Remote Sensing Letters,2011,9(1):13-17.

[13] PURANIKMATH S S,VANI K.Enhancement of SAR images using curvelet with controlledshrinking technique[J].Remote Sensing Letters,2016,7(1):21-30.

[14] BUADES A,COLL B,MOREL J M.A non-local algorithm for image denoising[J].IEEE Computer Society Conference on Computer Vision & Pattern Recognition.San Diego:IEEE,2005:60-65.

[15] PARRILLI S,PODERICO M,ANGELINO C V,et al.A nonlocal SAR image denoising algorithm based on LLMMSE wavelet shrinkage[J].IEEE Transactions on Geoscience & Remote Sensing,2012,50(2):606-616.

[16] CHEN S B,HOU J H,ZHANG H,et al.De-speckling method based on non-local means and coefficient variation of SAR image[J].Electronics Letters,2014,50(18):1314-1316.

[17] 刘书君,吴国庆,张新征,等.基于非局部分类处理的SAR图像降斑[J].系统工程与电子技术,2016,38(3):551-556.

LIU S J,WU G Q,ZHANG X Z,et al.SAR image despeckling via the classification-based non-local clustering [J].Systems Engineering and Electronics,2016,38(3):551-556.

[18] 陈世媛,李小将.基于自适应非局部均值的SAR图像相干斑抑制[J].系统工程与电子技术,2017,39(12):2683-2690.

CHEN S Y,LI X J.SAR image despeckling based on adaptive non-local means[J].Systems Engineering and Electronics,2017,39(12):2683-2690.

[19] APRIL G,ARSENAULT H H.Properties of speckle integrated with a finite aperture and logarithmically transformed[J].Journal of the Optical Society of America,1976,66(11):1160-1163.