水声信号熵特征提取与分类研究

付君宇 陈越超 权恒恒

(声纳技术重点实验室 第七一五研究所，杭州，310023)

近年来，迅速发展的非线性时间序列分析方法和基于混沌的信号处理理论，给水声信号处理提供了新思路。水声信号在产生和传播过程中存在非线性机制，而复杂海洋信道引起的信号畸变加大了特征提取和分类识别的难度。实际运用中，以经典傅里叶变换为基础的分析信号的功率谱特征和解调谱特征是识别领域最常用的处理方法。研究表明[1-4]，利用水声信号的非线性特征进行目标识别，是区别于传统频谱分析的有效手段。

熵能表征时间序列的复杂性，熵值越大表示信号越复杂，产生新模式的概率越大。Princus等提出的近似熵(Approximate Entropy)算法[5]，给时间序列的复杂度提供了一种可量化的统计指标并成功应用于生物时间序列分析。Richman[6]等人通过剔除近似熵算法中的自匹配情况，得到了新的序列复杂度测量方法-样本熵(Sample Entropy)。Chen等人引入指数函数代替样本熵算法中的Heaviside二值函数，提出了模糊熵(Fuzzy Enropy)算法[7]，对体表肌电信号的提取和分类获得了较好的效果。本文以上述三种算法为基础，结合平稳小波变换，对实际水声信号的近似熵、样本熵、模糊熵进行特征提取，以期达到目标分类的效果。

1 熵特征提取

1.1 近似熵和样本熵

假设有N点的原始时间序列X=[x(i),x(i + 1 ),...x(N)]，此序列近似熵的计算步骤如下：

1、引入非负整数m对X进行相空间重构，按顺序得到N-m+1个m维矢量，即

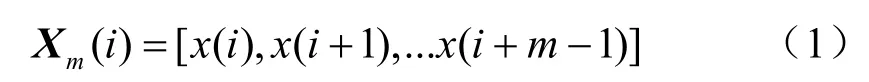
其中1 ≤ i≤ N - m +1。

2、计算重构矢量 Xm(i )与Xm( j )之间的距离，有

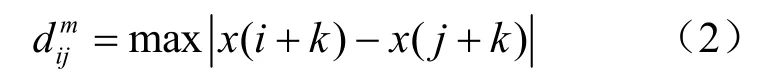
其中1 ≤ k ≤ m - 1 ,i ≥ 1 , j ≤ N - m +1。

3、统计小于给定相似容限r的数目num，并计算其与矢量总数的比值，记为

4、对C取对数，并求出对每个i的平均值，即

5、改变重构维数m=m+1，重复步骤1到4得到φm+1(r );

6、计算序列的近似熵ApEn：

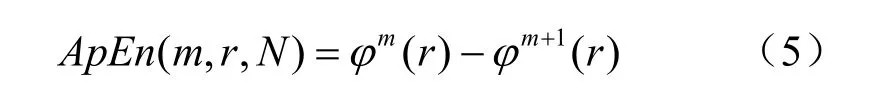
样本熵的计算过程与近似熵类似，需要注意的是，样本熵计算相似模式时先求和再求对数，并且重构矢量不进行自比较，即步骤2中的i不等于j，步骤3中重构向量总数为N-m，步骤4中先求和再取对数。

从理论上来说，熵是新信息产生率的测度，数据段的自比较没有任何意义，所以说实质上样本熵可以看做近似熵算法的改进。

1.2 模糊熵

时间序列 X = [ x(i),x(i + 1 ),...x(N )]的模糊熵计算过程如下：

1、重构矢量减去均值得新的矢量序列：

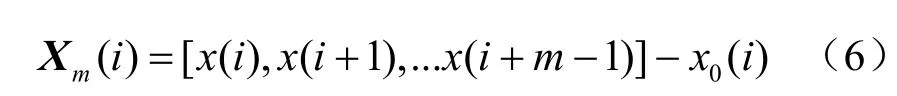
其中1 ≤ i ≤ N - m + 1 ， x0(i)为 x (i)的均值。

2、计算距离：

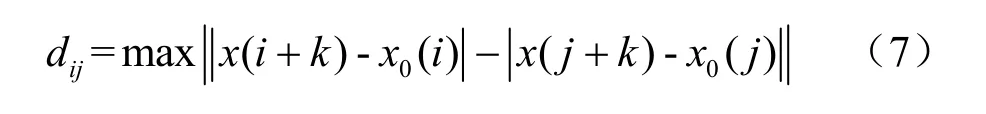
3、引入指数隶属度函数计算模式相似性：

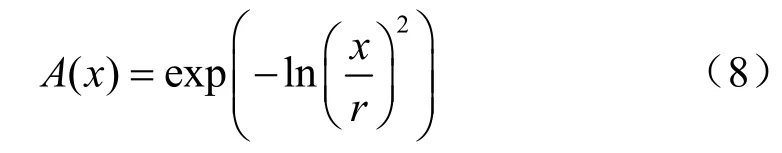
其中，令 x = dij，当x等于0时 A (x)取1，计算：

4、Aij求平均值得到：

5、改变重构维数m=m+1，重复步骤1到4得到φm+1(r )。

6、计算序列的模糊熵：

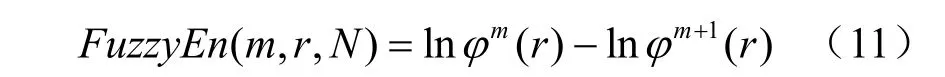
近似熵和样本熵的处理中，相似性由信号的绝对幅值差决定。而模糊熵算法首先通过均值运算除去了数据波动的影响，采用指数函数模糊化相似度度量公式。指数函数的连续性保证了模糊熵值随参数平稳变化。实际计算中N为有限值，重构维数m一般取1或者2，相似容限r范围在0.1SD～0.3SD之间(SD为时间序列的标准差)[8,9]，本文的计算中：m取2，r取0.2SD，点数N取2 048。

2 实验数据分析

试验采集得到A、B、C、D四种类型的水声目标信号，采样频率25 kHz。对四类目标原始信号进行滤波降采样处理之后，各取200个长度为2 048点的样本，分别提取近似熵、样本熵和模糊熵特征，结果如图1所示。可以看出，A类目标的近似熵、样本熵、模糊熵都明显小于其他三种目标类型，B、C、D三种目标类型的近似熵和样本熵接近，不具备可分性。另外，D类目标的模糊熵值最大，B、C两类目标的模糊熵虽然较A类和D类差异较大，但是此两类的模糊熵值很接近。

分别用K近邻（K-Nearest Neighbor，KNN）分类器和支持向量机（Support Vector Machine，SVM）两种分类器对特征提取的结果进行分类，其中，K取13，SVM的核函数使用径向基函数（Radial Basis Function，RBF）。对于每一类型的目标，随机选取200个样本中的70%作为训练样本，另外30%用来分类测试。

图1 四类目标的特征熵

表1 三种熵特征的分类结果

从表1的分类结果可以看出，A类目标的识别正确率均为 100%，说明近似熵、样本熵、模糊熵三种熵特征都能区分出A类型的目标，但是近似熵、样本熵特征无法区分B、C、D三类目标，而模糊熵特征可以明显区分出A、D，无法区分B类和C类目标。

综合来看，利用模糊熵特征的分类准确率要优于近似熵和样本熵。从理论上分析，一方面是因为在近似熵和样本熵的计算过程中，重构矢量相似性由 Heaviside函数决定，该函数的二值不连续性导致熵值的准确性和有效性出现问题。B、C、D三类目标的时域波形信号在幅度上差别很小，从绝对幅值差的角度出发，难以分辨出目标的差异。另一方面，模糊熵在进行矢量重构时，以去除均值后信号的相对误差代替信号幅值的绝对误差，同时利用具有连续取值的指数函数度量相似性，在一定程度上提高了熵值区分不同目标的能力。

考虑到B类目标和C类目标的识别率较低，下面对原始信号做平稳小波变换(Stationary Wavelet Transform，SWT)之后的近似成分和细节成分再分别提取以上三种熵特征。SWT不对信号采取降采样，而对滤波器系数进行插值，因而得到与原信号长度相同的近似信号和细节信号，具有平移不变性，避免了时移信息的丢失，能够更好地在空间上与原信号相对应[10]。处理中选择常用的db3小波基，对信号做5层分解。图2给出了第一层近似信号和细节信号的熵特征提取结果。

图2 SWT后熵特征提取结果

表2的分类结果表明，经过SWT变换后得到的近似信号，仍然无法分出B类和C类目标；而细节信号利用模糊熵特征，B类、C类目标的识别准确率分别提高到了96.7%、100%，整体平均识别率达到了98.55%，较好地区分了四种目标类型。文中选取的数据样本为相较慢变化的低频成分，时间长度较短，样本信号序列中自然会包含更多的高频信息。近似信号反映了原始信号的低频信息，细节信号反映的是高频成分。利用细节信号提取模糊熵特征，分类准确率高，说明文中四类目标低频成分相似度较高，差异主要体现在高频端，这给目标的准确识别提供了有效的信息。

表2 四类目标近似信号和细节信号的模糊熵分类结果

3 结论

本文结合近似熵、样本熵、模糊熵特征提取算法与平稳小波变换，通过对A、B、C、D四类实测水声目标信号做特征提取和分类研究，分析总结得到如下结论：

（1）模糊熵特征相比近似熵和样本熵特征有较好的连续性和准确性，实际分类结果表明，模糊熵可以作为区分水声目标类型的有效特征。

（2）通过SWT提取信号的低频成分和高频成分，再进行特征提取作分类研究，可以在一定程度上提高目标分类的准确率。

（3）模糊熵为目标识别提供了一定参考信息，实际运用中，计算参数的选择和算法的实时处理还需做更深入的研究。

参考文献：

[1] 李钢虎, 李亚安, 贾雪松. 水声信号的混沌特征参数提取与分类研究[J].西北工业大学学报,2006,24(2)：170-174.

[2] 章新华,林良骥. 船舶辐射噪声的混沌现象研究[J].声学学报,1998,23(2)：134-140.

[3] 赵犁丰, 宋洁, 姚玉玲, 等. 利用小波包分析和混沌特征提取进行船舶辐射噪声分类[J]. 中国海洋大学学报自然科学版,2004,34(6)： 1036-1040.

[4] 凌继平,黄定东,邓异,等. 基于递归图和近似熵的水下目标特征提取方法[J].计算机与数字工程,2011,39(11)：147-150.

[5] PINCUS S M. Approximate entripy (ApEn) as a complexity measure[J]. Chaos,1995,5(1)：110-117.

[6] RICHMAN J S, MOORMAN J R. Physiologicak timeseries analysis using aooroximate and sample entropy[J].Amer J Physiology--Heart Circulatory Physiology, 2000,278(6)： 2039-2049.

[7] CHEN WEITING, WANG ZHIZHONG, XIE HONGBO.Characterization of surface EMG signal based on fuzzy entropy[J].IEEE Transactions on Neural Systems and Rehabilitation Engeering,2007,15(2)：267-272.

[8] 李立,曹锐,相洁. 脑电数据近似熵与样本熵特征对比研究[J]. 计算机工程与设计,2014,35(3)：1021-1026.

[9] 孙克辉,贺少波,尹林子,等.模糊熵算法在混沌序列复杂度分析中的应用[J]. 物理学报, 2012, 61(13)： 71-77.

[10] 刘建国,李志瞬,刘东. 基于平稳小波变换及奇异值分解的湖底回波分类[J]. 声学学报,2006,31(2)：167-172.