正交试验下槽形梁桥瞬态噪声影响分析*

曾 峰刘林芽

（1.广深铁路股份有限公司广州工务段，510610，广州；2.华东交通大学土木建筑学院，330013，南昌∥第一作者，助理工程师）

轨道交通高架桥结构因其建设周期短、断面空间利用率高、造价低等优势，得以广泛应用。但其低频噪声的投诉也日益增加，已成为制约其发展的主要因素［1-2］。

文献［3］发现，列车通过高架桥时的桥梁结构噪声属于低频噪声。文献［4］发现，阻尼增大会导致桥梁辐射噪声降低。文献［5］研究表明，铁路桥梁的阻尼比会导致结构体系振动响应的减小，而对结构噪声的影响尚无权威定论。文献［6］研究表明，轨道板的刚度越大，移动荷载产生的声压就越大。文献［7］研究发现，增加轨道板的刚度，可以减小噪声辐射。文献［8］研究表明，仅改变光滑圆柱结构的刚度不能有效降低其辐射声压级。

综合以上研究发现，现有桥梁结构噪声研究主要集中在频域内，轨道交通噪声影响评价指标与时域密切相关。针对轨道交通槽形梁结构参数对瞬时噪声影响的研究，尚存在争议，无权威定论。因此，开展桥梁结构噪声影响参数的时域仿真分析十分必要。

本文以某拟建的30 m长轨道交通简支槽形梁为研究对象，结合有限元-瞬态边界元法，根据桥梁支座刚度、桥梁阻尼比及桥梁结构刚度等影响因素及水平，设计了16组正交试验，以分析不同结构参数组合的槽形梁声辐射特性。

1 正交试验设计

试验在桥梁跨中截面选取线路中线底板正下方4 m场点（场点1）作为近声场评价场点，选取距线路中线25 m的场点作为远声场评价场点（如图1所示）。

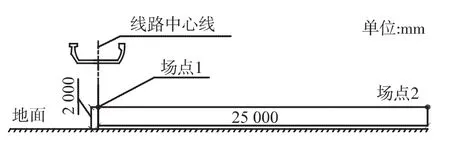
图1 正交试验声学场点分布图

据统计，目前的铁路桥梁阻尼比大多为0.01～0.05。本试验参考文献［10］，针对城市轨道交通通用桥梁支座（橡胶减振支座），实测得到铅芯橡胶支座竖向刚度。

本文选取桥梁支座刚度、桥梁阻尼比、桥梁结构刚度等3个因素进行正交试验。并将每个因素划分为4级水平（如表1所示）。

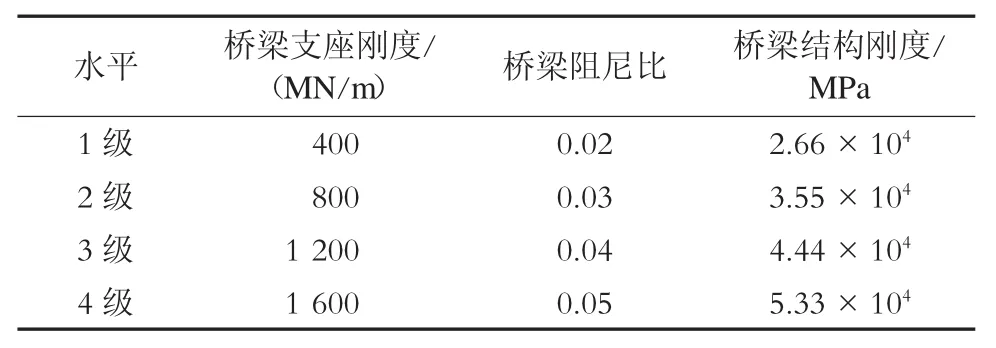
表1 桥梁正交试验影响因素水平划分

2 轨道交通高架槽形梁模型

2.1 有限元模型

建立轨道交通高架槽形梁有限元模型时，梁体、轨道板及CA（水泥沥青）砂浆层等采用Solid45单元，桥梁弹性支座和钢轨扣件采用Combin14单元，钢轨选用梁单元Beam188。由于只分析梁体的结构噪声，忽略了桥墩对结构声辐射的影响，因此，采用固定约束模拟桥墩。具体轨道结构参数见表2。

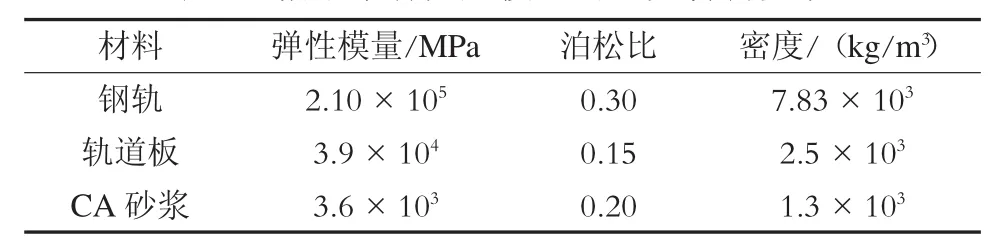
表2 槽形梁有限元模型的主要材料参数

简支槽形梁有限元模型如图2所示。梁体跨中截面腹板一侧为圆弧结构，另一侧采用直线折斜腹式的不对称结构。各项参数经过多次调试，能满足GB 50157—2013《地铁设计规范》（文献［9］）的要求。

2.2 瞬态边界元模型

图2 槽形梁有限元模型

将基于有限元法求解的桥梁瞬态动力响应结构，通过插值的方法分配到桥梁结构声学边界元网格上，并作为边界条件，进而求解出槽形梁的瞬态声辐射特性的方法，就是瞬态边界元法。槽形梁的表面为封闭的边界表面，通过对其离散，可得到边界元求解方程：

Ap（ra）=Bvn（ra）（1）

式中：

A——声压系数矩阵；

B——方向速度系数矩阵；

p（ra）——封闭边界表面Ωa的声压；

vn（ra）——封闭边界表面Ωa的方向速度。

槽形梁表面外部无限域内任意一点的声压可以通过Helmholtz积分方程求得。

瞬态边界元法用于计算桥梁结构振动声辐射问题时，不仅能合理反映列车荷载作用下桥梁辐射噪声在时间域的分布情况，还避免了采用模态叠加法出现的模态截断误差，使计算精度更有保障。

基于瞬态边界元理论建立的槽形梁结构声辐射边界元模型如图3所示。在进行瞬态边界元计算时，边界元网格必须是三角形网格，故采用自由网格划分。

图3 槽形梁边界元模型

2.3 轮轨激振力求解与加载

轨道交通槽形梁结构声辐射求解的关键问题就是激振源的获取。模拟试验通过SIMPACK多体动力学软件获取轮轨激振力。其中，地铁车辆包括车体、轮对、转向架等刚体,以及一系、二系弹簧等力元，轨道不平顺选用美国6级不平顺谱。经计算，列车以80 km/h运行时的垂向轮轨作用力时程曲线如图4所示。

3 槽形梁瞬态噪声响应正交分析

3.1 正交分析表设计

为了在不影响各个因素条件下，大大减少试验次数，也为了避免由主观经验造成的试验次数盲目性和试验结果的无代表性，选用正交表。得到的正交分析表如表3所示。

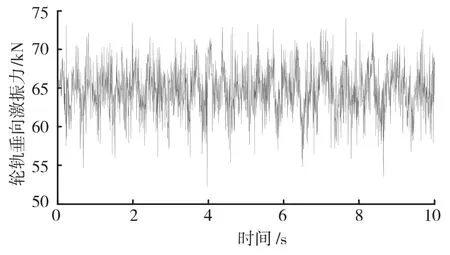
图4 轮轨垂向激振力

3.2 槽形梁结构瞬态噪声正交试验分析

表4分别为正交试验下桥梁结构噪声各影响参数的极差分析。根据极差R的大小，判断因素的主次影响顺序。R越大，表示该因素的水平变化对试验指标的影响越大，因素越重要。由表4可知，在结构辐射噪声近声场处，R3＞R2＞R1，桥梁结构阻尼比对槽形梁结构噪声影响较为显著，通过增大结构阻尼比将在一定程度上减少结构的瞬态噪声水平。由表4可知，在结构辐射噪声远声场处，R2＞R3＞R1，从R的大小可知，桥梁支座刚度对槽形梁结构噪声影响较小，桥梁结构刚度与桥梁结构阻尼比对近声场瞬态结构噪声影响较为显著。

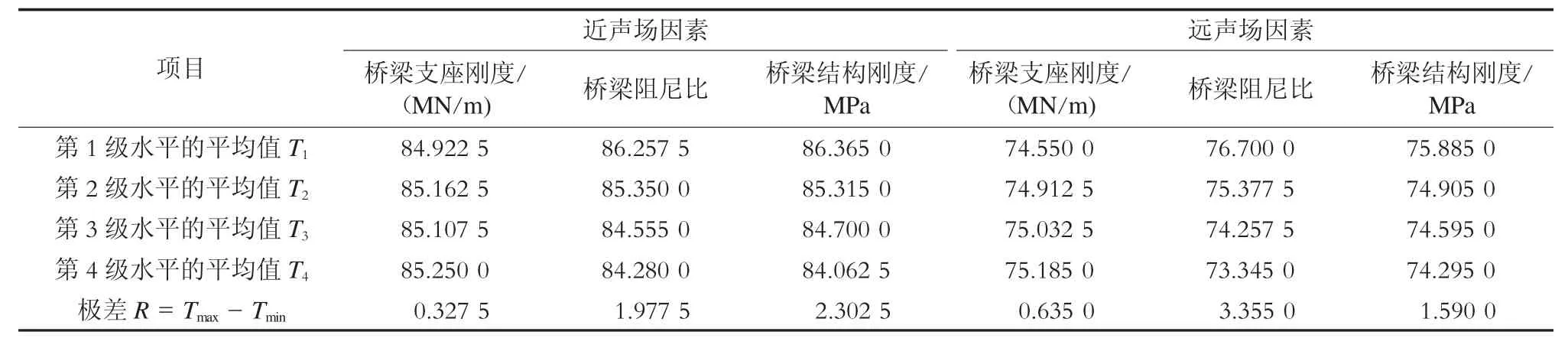
表4 桥梁结构辐射噪声近声场处和远声场处各因素极差分析

为了更好地反映因素与响应指标之间的变化趋势，以各因素水平级别为横坐标，场点瞬态最大线性声压级的平均值为纵坐标，绘制结构辐射噪声近声场及远声场影响参数变化趋势图，见图5～6。

由图5可知，随着桥梁阻尼参数和结构刚度系数的增大，场点最大线性声压级逐渐减小，但增大量随参数的增大而逐渐减小。由图6可知，桥梁结构支座刚度对低频瞬态辐射噪声影响较小，桥梁结构刚度达到4.44×104MPa之后，对远声场辐射噪声影响较小。

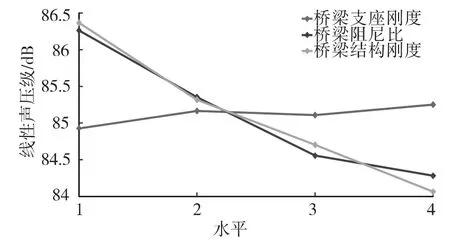
图5 槽形梁结构辐射噪声近声场各水平变化趋势

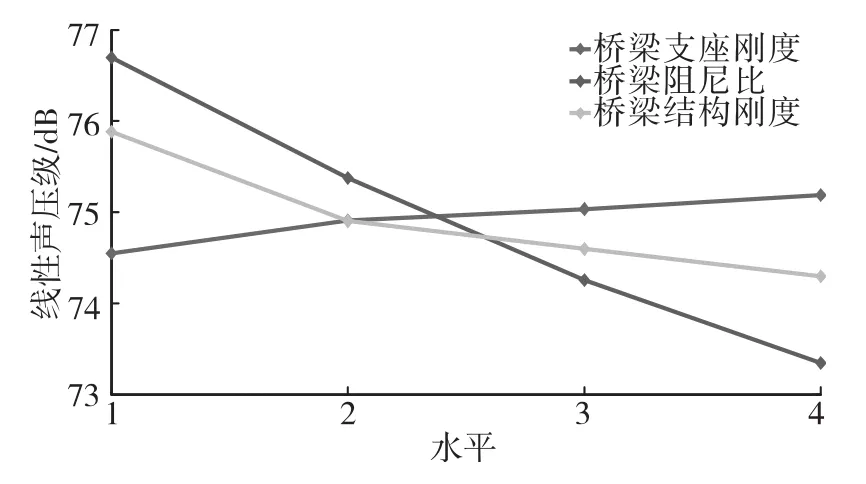
图6 槽形梁结构辐射噪声远声场各水平变化趋势

4 结论

本文针对槽形梁桥结构辐射噪声问题，从瞬时结构噪声出发，探讨分析了辐射特性及因素影响，通过数值分析得到以下结论∶

（1）轨道交通槽形梁结构瞬态辐射噪声对桥梁阻尼比和结构刚度的改变较为敏感，随着桥梁阻尼参数和结构刚度系数的增大，场点最大线性声压级逐渐减小。

（2）在结构辐射噪声近声场处，桥梁结构刚度对槽形梁结构噪声影响较为显著；在结构辐射噪声远声场处，桥梁阻尼比对槽形梁结构噪声影响较为显著。

（3）针对轨道交通槽形梁结构噪声优化控制时，可以适当提高槽形梁梁体的整体结构刚度或增加桥梁结构的阻尼比。

［1］ 雷晓燕，圣小珍.现代轨道理论研究［M］.北京：中国铁道出版社，2008：359.

［2］ 李奇，吴定俊.混凝土桥梁低频结构噪声数值模拟与现场实测［J］.铁道学报，2013，35（3）：89.

［3］ NGAI K W，NG C F.Structure-borne noise and vibration of concrete box structure and rail Viaduct［J］.Journal of Sound and Vibration，2002，255（2）：281.

［4］ STUBER C.Air-and structure-borne noise of railways［J］.Journal of Sound and Vibration.1975，43（2）：2819.

［5］ 李宝银.高速铁路32 m简支箱梁结构噪声研［D］.北京：中国铁道科学研究，2014.

［6］ AU F T K，WANG M F.Sound radiation from forced vibration of rectangular orthotropic plates under moving loads［J］.Journal of Sound and Vibration，2005，281（3-5）：1057-1075.

［7］ KIMURA S，INOUE K.Practical of floor impact sound by impedance method［J］.Applied Acoustics，1989，26（4）：263.

［8］ 谢伟平，陈西德.钢筋混凝土圆柱壳声辐射特性的有限元研究［J］.声学技术，2008，27（5）：769.

［9］ 中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局.地铁设计规范：GB 50157—2013［S］.北京：中国建设工业出版社，2013.

［10］ 吴彬.铅芯胶支座力学性能及其在桥梁工程中的减、隔振应用的研究［D］.北京：铁道科学研究院，2003.