跳跃风险的外溢效应与投资价值

刘庆富,张金清

(复旦大学金融研究院,上海200433)

1 引 言

随着金融自由化程度的加深,中国与美国期货市场之间的关联性日渐紧密.中国期货市场对美国市场施加自身影响的同时也不得不承受来自美国市场波动的冲击[1].其中,由于期货价格的大幅波动而带来的风险,常称之为跳跃风险1与连续的小幅的价格波动相比,大幅的波动常表现为非连续的跳跃[2]..并且,在这些冲击中,尤以跳跃风险对中国期货市场的影响最大2跳跃风险往往与知情交易者有关[3],且多属于系统性风险[4]..然而,大量事实表明,这些跳跃风险的背后,常伴随着风险事件的发生3与两市场收益之间的关系相比,期货市场波动含有大量的信息,是市场风险的主要来源,且具有风险累积和传染效应,对另一期货市场的影响往往很大;因此,本文将重点研究美国同步和异步期货市场的跳跃风险对国内期货市场的风险传递效应及其风险绩效..这些跳跃风险得到了期货交易者,期货交易所及监管当局的广泛关注4为防范跳跃风险的发生,上海期货交易所,大连商品交易所和郑州商品交易所均采用了涨跌停板制度及春节期间增加保证金的收取比例等举措.,但对期货市场的跳跃风险传导机制与投资价值的研究仍有待深入.

在跳跃风险传导机制方面,现有研究有些集中于风险事件对资产价格的影响[5-9],有些并不把风险事件加以具体区分,而是对市场上出现的所有跳跃风险进行研究[10-12].然而,这些研究多针对某一市场而言的,并没有分析跳跃风险在多个市场上的信息传递关系.为此,De Bandt等[13]从定性角度总结了作为系统性的跳跃风险在银行间跨境传递的证据;之后,Asgharian等[10]利用SVCJ风险模型研究了国际股票市场之间的跳跃溢出行为,发现不同国家股票市场之间存在显著的跳跃溢出效应,且处于同一地区和相同工业结构的股票市场之间的跳跃溢出程度更大.类似地,刘庆富等[14]对中国与美国异步商品期货市场之间的跳跃溢出行为进行了初步分析,发现中国与美国期货市场之间存在显著的跳跃溢出,且美国对中国的跳跃溢出存在“一日滞后”效应.这一研究的主要对象是针对中国和美国(白天)正规(异步)交易市场进行的,并没有对美国同步的电子交易期货市场展开研究5自1992年6月以来,已有很多国家加入了Globex电子交易系统,加入这一系统的交易所可以实现昼夜全天候交易(CME,2010),如伦敦金融交易所(LME),芝加哥商品交易所(CBOT)和纽约商品交易所(NYMEX)等..然而,由于通信技术和网络技术的飞速发展,与中国期货交易相同步的美国电子交易市场的价格变动会在瞬间传递到国内,其影响程度变得越来越不可忽视,其影响力也似乎有加速趋势.例如,NYMEX铜期货交易在Globex电子市场上的交易量占总交易量的比重已从2004年的18.4%上升至2010年的40.5%,平均占比为37.9%.若仅考虑美国正规交易市场的跳跃风险对中国期货市场的影响,势必会忽略电子交易市场更多富有价值的信息,其结论的可靠性也必将大打折扣.并且,近年来国际期货市场的大幅波动频繁发生,有愈演愈烈的趋势[15,16].

在投资价值方面,相关研究主要集中于跳跃风险的分散化与跳跃风险溢价.对前者而言,Jarrow等[17]和Ball等[18]发现跳跃风险是可以通过股票的投资组合进行分散的;Wu[19]和Kurmann[20]认为跳跃风险对投资组合的配置不仅具有重要影响,且能够改变投资组合的配置;Liu等[21]发现,跳跃溢出明显降低了能源期货的投资组合收益.对后者而言,Wright等[22]发现跳跃风险能够预测超额的债券收益;Broadie等[23]对期货期权的跳跃风险溢价进行了研究;Todorov[24]利用连续时间的跳跃风险溢价变量解释了隐含和现实波动的动态特征;同时,Todorov等[25]利用二次变差研究了跳跃的贝特值,发现跳跃的贝特值要大于连续的贝特值;之后,Chan等[26]发现,DAX,FTSE,Nikkei和S&P500股指期货的收益时变跳跃风险溢价是显著存在的.

在这一趋势下,美国期货市场的跳跃风险对中国期货市场是否有影响?如果影响存在,影响的方向和力度怎样?是否具有杠杆效应?有何趋势?并且,这些跳跃溢出是否具有哪些投资价值?这些问题尚不十分清楚.为此，本文将从四个方面展开研究：第一,不同于现有的波动溢出研究,本文既考虑美国期货正规交易市场的跳跃风险对中国期货市场的异步影响,也考虑美国期货Globex电子交易市场的跳跃风险对中国期货市场的同步影响;第二,为研究其影响趋势,本文将对加入WTO过渡期间和过渡期后的样本分别展开研究6中国加入世界贸易组织(World Trade Orgnization,WTO)的过渡期为2001年12月11日至2005年12月11日..第三,在分段考虑的基础上,从投资组合分散化角度分别给出中国期货市场剔除跳跃风险溢出和含有跳跃风险溢出情况下美国期货市场跳跃风险对中国期货市场的贡献度以及跳跃风险溢出绩效;第四,从风险溢价角度,给出中国加入WTO过度期间和过渡期后的期货市场的跳跃风险溢价,并对其进行了分析和比较.

2 研究方法

2.1 双变量SVIJ模型及其估计方法

假设中国或美国的期货价格为Yt=ln(Ft),SVIJ模型的随机微分方程为

其中t—为时间t前与之最近的时间点,且是R上的标准维纳过程;ρ为式(1)和式(2)波动率之间的相关度;是分别带有常数强度λy和λv的泊松过程,ξy和ξv分别为收益和波动的跳跃大小,且之所以选择SVIJ模型,是因为源于收益和波动跳跃的独立跳跃能够较全面地刻画市场的跳跃特征,其参数估计效果均比SV,SVJ和SVCJ模型都要好[12].

在t时刻的跳跃可用如下公式来估计

其中t=1,2,...,T,1{·}为示性函数,l为阈值.l的选择是通过估计隐含跳跃和估计跳跃之间平均间隔最小来实现的[27],其近似等于λ的估计值.为更具可比性,阈值将取中美期货市场跳跃的平均值.

2.2 跳跃风险溢出指标的建立

利用SVIJ模型所估计的潜在历史跳跃次数和跳跃大小,分别构建美国期货对中国期货市场的跳跃溢出概率,跳跃溢出强度和跳跃溢出大小指标.

1)跳跃溢出概率指标

美国对中国期货市场的跳跃溢出概率(jump spillover probability,JSP)是指美国期货市场的跳跃能够引起中国发生跳跃的概率.由于美国具有同步的电子交易和异步的正规交易两个市场,美国对中国的同步交易和异步交易的跳跃溢出概率指标可分别表示为

跳跃溢出概率的显著性可通过检测跳跃溢出概率与零假设下独立跳跃的相伴概率来实现[10].

2)跳跃溢出强度指标

美国对中国期货市场的跳跃溢出强度(jump spillover intensity,JSI)是指美国期货市场的跳跃能够引起中国发生跳跃的程度.美国对中国同步交易和异步交易的跳跃溢出强度指标可分别表示为

与Asgharian和Bengtsson[10]的研究方法类似,美国对中国期货市场跳跃溢出强度的显著性是通过检验估计的跳跃溢出强度是否要比零假设下完全独立的不同期货市场溢出强度更高而得到的.

3)跳跃溢出大小指标

美国对中国期货市场的跳跃溢出大小(size of jump spillover,SJS)是指美国期货市场的跳跃引起中国发生跳跃溢出的幅度.如此,美国对中国同步交易和异步交易的跳跃溢出大小指标可分别表示为

2.3 跳跃风险溢出的投资价值评估模型

1)跳跃风险溢出贡献度模型

美国对中国期货市场的跳跃风险溢出贡献度（contribution of jump risk spillover,CJRS）可表示为跳跃溢出概率与跳跃大小之积,然后除以总溢出概率与总跳跃大小之积.美国对中国同步交易和异步交易的跳跃风险溢出贡献度可分别表示为

2)跳跃风险溢出的投资组合夏普比率模型：基于投资分散化的视角

为计算含有和不含有跳跃溢出的中国期货资产组合绩效,采用的夏普比率公式为

设含有跳跃风险溢出的资产组合i和不含跳跃风险溢出的资产组合j的假设检验为

3)跳跃风险溢出的风险溢价模型：基于跳跃风险溢价的视角

由公式(2),Euler离散化的时变的跳跃波动率为

假设美国期货市场发生的跳跃能够引起中国期货市场发生跳跃的波动率记为(其中代表由极端事件(消息)引起的跳跃波动部分;那么,中国期货市场没有发生跳跃的波动率将记为代表由正常事件(消息)引起的正常波动部分.由此,与Eraker[30],Broadie等[23],Chan等[26]的跳跃风险溢价模型类似,美国对中国的跳跃风险溢价回归方程为

其中Rt=ln(Pt/Pt-1)为中国期货收益,φNJ和φJ分别为正常波动和跳跃波动参数,δNJ,t和δJ,t分别为单位正常波动和跳跃波动的风险溢出价格8公式(18)将采用加权普通最小二乘法来进行估计;类似于式(16),参数的显著性将采用基于正态分布的均值检验方法..

进一步地,美国对中国期货市场产生上跳和下跳的跳跃风险溢价回归方程为

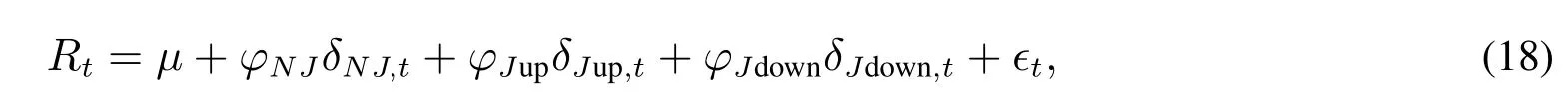
其中φJup和φJdown分别为上跳和下跳跃波动参数，δJup,t和δJdown,t分别表示上跳和下跳风险溢价.

3 中美期货数据的选择及其统计特征分析

3.1 数据选择

本文首先对中美期货市场及其数据进行选择.中国期货市场将选择上海期货交易所的铜期货和大连商品交易所的大豆期货每个交易日的收盘价格作为代表;鉴于美国期货市场是非常成熟且具有很强国际定价能力的市场,美国期货市场将选择纽约商品交易所(NYMEX)的铜期货和芝加哥商品交易所(CBOT)的大豆期货每个交易日的收盘价格作为美国期货异步交易市场以及CME Globex的铜和大豆即时期货价格作为同步交易市场的代表.之所以选择铜和大豆期货市场,主要是因为：第一,截止到2010年底,中国铜和大豆期货的交易量仍位居世界第二,是最具吸引力的新兴市场,对国际期货市场具有显著的影响,因而,选择这两个期货品种应具有较强的代表性;第二,相对于发达市场,由于交易成本,交易规则,流动性,投资群体结构及制度性因素的约束,我国市场仍不成熟,因此,探讨美国期货市场对中国的影响对中国期货本身而言就显得非常必要.为具有可比性,铜和大豆期货的时间跨度均从2002年1月2日∼2010年12月31日,共得到2 340组铜和大豆期货价格数据.此外,为研究中国加入WTO过渡期间和过渡期后美国期货市场跳跃溢出风险对中国期货市场的影响及其趋势,数据分为两个时段：2002年1月2日∼2005年12月11日的“过渡期间”与2005年12月12日∼2010年12月31日的“过渡期后”.中国期货价格数据来源于Wind数据库,美国数据则来源于CME数据库.

由于中国和美国市场所处时区不同,期货交易的时间也存在诸多差异(如表1所示).纽约商品交易所的交易时间为20：10至次日1：00,芝加哥商品交易所的交易时间为22：30至次日2：15,中国期货市场与NYMEX/CBOT的正规交易时间是互不重叠的;在CME Globex电子交易市场中,NYMEX的电子交易时间为5：00 至次日的4：15,CBOT 的电子交易时间为6：00至19：15与21：30至次日0：15,由此看来中国期货的交易时间已处于NYMEX/CBOT的电子交易时间之中.如前文所论,中国期货市场不仅受到正规交易价格的影响,也受到Globex电子交易价格的冲击.为研究美国正规交易和电子交易期货市场跳跃风险对中国期货市场的影响,本文除了选择美国正规交易市场的日交易收盘价格作为中国和美国期货市场异步交易的研究对象之外,还选择了与中国期货市场收盘时(即北京时间15：00)相对应的美国电子交易价格(即Globex铜期货价格选择的时点为美国东部时间上午3：00的收盘数据,而大豆期货价格选择的时点为美国中部时间上午2：00的收盘数据)作为中国和美国期货市场同步交易的研究对象9考虑异步交易时,本文将检测美国期货正规交易市场收盘价格对即将到来的中国期货市场收盘价格的影响状况,这时的美国期货市场在时间上应领先于中国期货市场;考察同步交易时,本文将考察美国Globex电子交易价格对同时正在交易的中国期货市场收盘价格的影响状况,此时的美国期货市场在时间上与中国期货市场完全同步..

表1 中国和美国期货市场的交易时间表Table 1 The schedule of Chinese and U.S.futures markets

3.2 数据的统计特征分析

图1∼图2分别给出了中国铜和大豆期货价格和美国同步(电子)交易和异步(正规)交易期货价格的运动趋势图10中国期货价格参照左坐标轴,美国期货价格参照右坐标轴..可以看出,中国和美国期货市场的运动趋势基本一致,存在很强的联动性11夏天等[32]、华仁海等[33]及Liu等[1]认为,中美两国期货市场之间不仅存在较强的相关度,还具有协整关系..从纵向看,中美期货价格的波动比较剧烈,如大豆在2003年4月至2004年6月间波动较大,2006年1月以后的铜也处于巨大波动之中.鉴于此，以2005年12月11日(中国履行WTO协议全面对外开放的时间)为分界点,来研究中国加入WTO过渡期间(2002年1月2日∼2005年12月11日)和过渡期后(2005年12月12日∼2010年12月31日)美国市场的跳跃风险对中国市场的影响及其趋势;直观上,与过渡期间相比,过渡期后中美期货价格的均价不仅有了很大提高,且市场波动也明显加大.

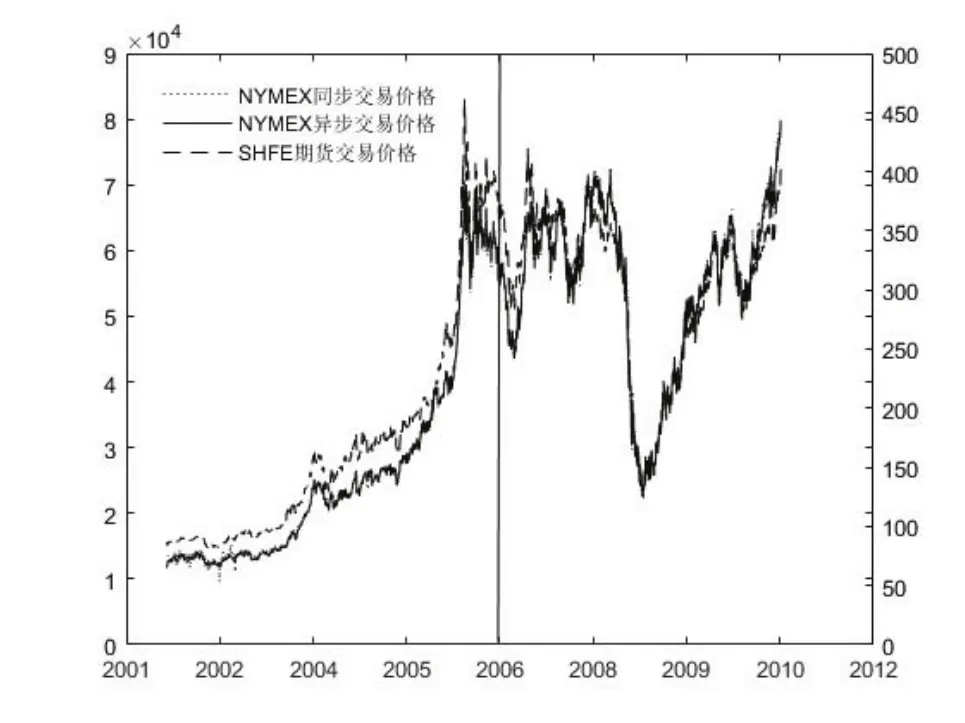
图1 SHFE与NYMEX铜期货同步和异步交易价格趋势图Fig.1 The price trends of synchronous and non-synchronous trading in copper futures markets

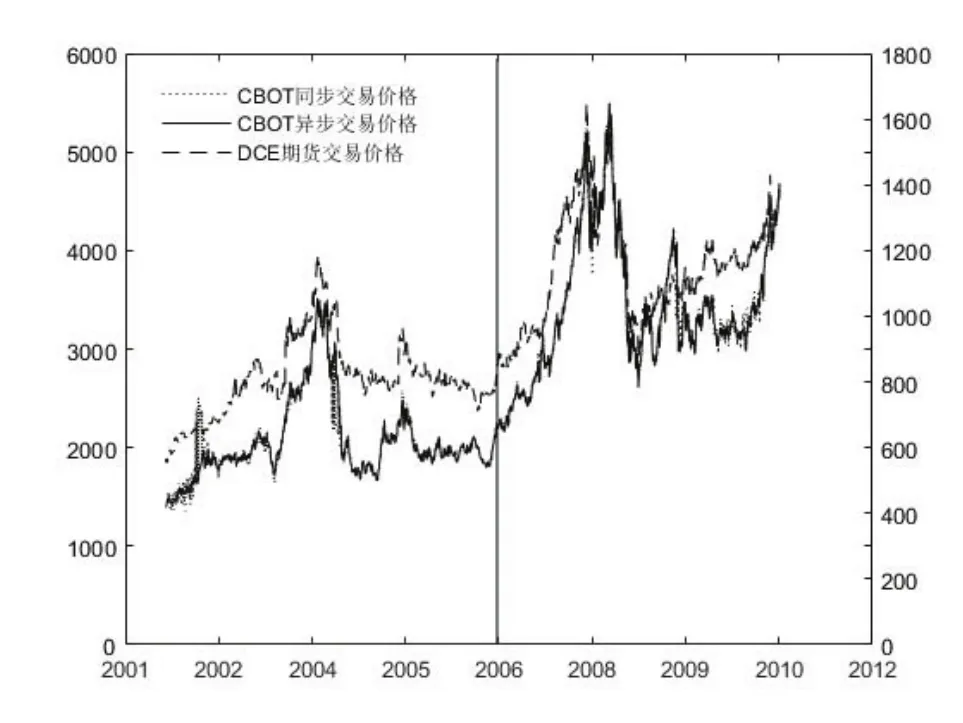
图2 DCE与CBOT大豆期货同步和异步交易价格趋势图Fig.2 The price trends of synchronous and non-synchronous trading in soybean futures markets

表2给出了中美期货市场收益的基本统计量.可以看出,中美期货的年化收益均大于零,过渡期间的铜收益明显大于过渡期后的收益,而大豆收益则相反;与过渡期间相比,过渡期后的期货市场风险明显增大了;收益的偏度基本为负,具有厚尾特性,这意味着期货收益必然存在诸多“跳跃”.此外,加入WTO过渡期间和过渡期后的中美期货收益均为平稳序列.以上特征为SVIJ模型的选择提供了证据12与Eraker[12]类似,本文利用SV,SVJ,SVCJ和SVIJ模型进行了实证分析，发现SVIJ的拟合度是最好的,这与Eraker[12]的结论相一致..

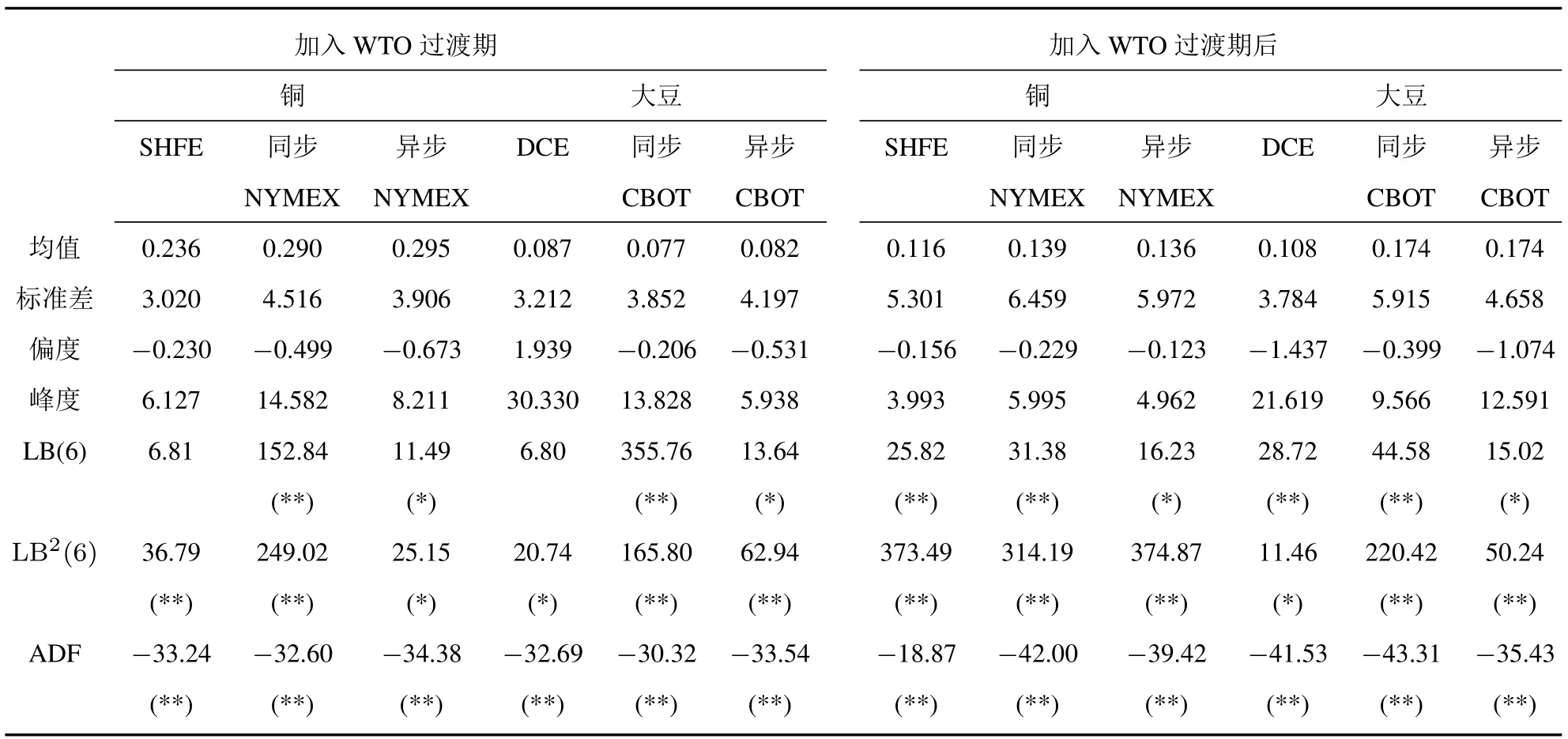
表2 中国和美国期货市场收益的基本统计特征Table 2 The descriptive statistics of returns in Chinese and U.S.futures markets

4 实证分析

4.1 基于SVIJ模型的参数估计结果

本部分对中美铜和大豆期货市场进行了实证分析.试验共模拟5万次,烧去1万次,剩余4万次作为参数估计的后验均值样本.表3给出了加入WTO过渡期间和过渡期后中美期货市场基于SVIJ模型的参数估计结果.可以看出,无论在加入WTO过渡期间还是在过渡期后,µY均为负,这意味着跳跃多与坏消息有关;相对地,过渡期后的数值明显小于过渡期间.ρ均为负,美国同步和异步交易的相关性均强于中国期货市场,且过渡期后的数值明显小于过渡期间.λV大于λY,说明波动跳跃总体上要大于收益跳跃,过渡期后的波动跳跃和收益跳跃均大于过渡期间.13实证结果还发现，基于SVIJ模型的波动跳跃概率显然能被很好地估计,波动跳跃呈现出稀疏性,非对称性和高波动时期下的集聚效应.并且,中美同步交易和异步交易市场之间均存在着很强的相依关系.

为更具可比性,选择各样本的平均值0.060 8来作为共同的阈值.这样,在识别出美中期货市场的跳跃之后,来分析一下美国期货跳跃风险对中国的直观影响.表4给出了过滤跳跃前后美中期货市场收益和波动之间的相关度.发现过滤跳跃前后美国和中国期货市场之间的相关度绝大多数为正,且均在5%的水平下显著,过滤跳跃前美中同步交易市场之间与美中异步交易市场之间的相关度均明显大于过滤跳跃后.这说明跳跃的存在强化了美中期货市场之间的相依关系.并且,通过比较同步和异步交易市场之间的相关性可以看出,对收益而言,同步交易市场之间的相关度大于异步交易市场之间的相关度;对波动而言,除铜期货市场过滤跳跃后的情况外,其它样本同步交易市场之间的相关度均小于异步交易市场之间的相关度.此外,通过比较加入WTO过渡期间和过渡期后的相关性可以看出,过渡期后美中期货市场之间的相关度也明显大于过渡期间的相关度.这些发现表明跳跃因素在维系美国和中国期货市场之间关系时,扮演着非常重要的角色,也同时意味着美国期货市场的跳跃风险对中国期货市场的影响是绝不可忽视的,这为下文进一步研究美国期货市场跳跃风险对中国的影响提供了又一证据.

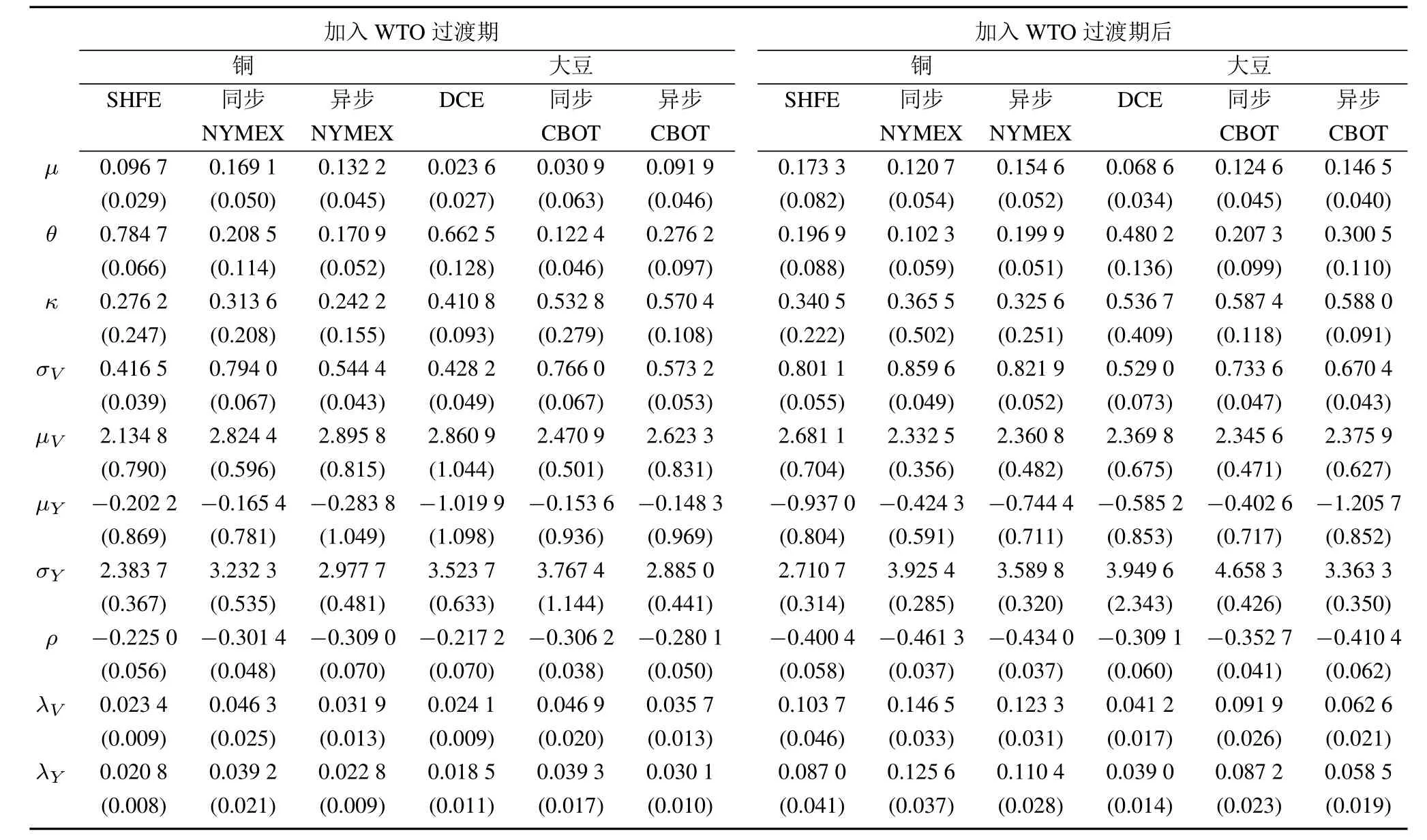
表3 中国和美国期货市场基于SVIJ模型的参数估计结果Table 3 The coeff i cient estimation of SVIJ model in Chinese and U.S.futures markets

表4 过滤跳跃前后美国和中国期货市场的相关度估计值Table 4 The correlation before and after f i ltering jumps in Chinese and U.S.futures markets

4.2 美国期货市场跳跃风险对中国期货市场影响的实证分析

在识别出美国和中国期货市场的波动跳跃之后,利用前文的跳跃溢出概率,跳跃溢出强度以及跳跃溢出大小测度指标,即可计算出美国期货市场跳跃风险对中国期货市场的影响状况.

1)美国对中国期货市场跳跃溢出概率的测度结果

表5给出了美国期货同步和异步交易市场对中国期货市场的跳跃溢出概率.实证结果发现,美国期货同步和异步交易市场的跳跃风险对中国期货市场的跳跃溢出概率均较大,且均在5%的水平下统计显著.从样本(包括全样本,过渡期间和过渡期后样本)的估计结果看,美国期货同步交易市场对中国期货市场的跳跃溢出概率明显大于美国异步交易市场对中国期货市场的跳跃溢出概率;也就是说,美国Globex电子交易市场对中国期货市场的影响要大于美国正规交易市场对中国期货市场的影响.并且,无论是Globex电子交易市场还是正规交易市场,美国铜期货市场的跳跃风险对中国铜期货市场的冲击能力显著大于美国大豆期货市场对中国大豆期货市场的冲击能力.同时,通过比较加入WTO过渡期间和过渡期后的冲击程度来看,过渡期后美国期货市场的跳跃风险对中国期货市场的冲击程度比过渡期间明显加强了,这意味着中国加入WTO以后,美国期货市场对中国期货市场的影响能力明显增强了.此外,作者还对美国期货市场好的(即好消息所影响的)和坏的(即坏消息所影响的)跳跃风险对中国期货市场的影响进行了分析,发现向下跳跃的概率值均大于向上跳跃的概率值,这说明美国期货市场基于坏消息的跳跃风险对中国期货市场的影响要大于同等程度的基于好消息的跳跃风险对中国期货市场的影响,即美国期货市场的跳跃风险对中国期货市场的影响具有杠杆效应.

表5 美国期货市场对中国市场的跳跃溢出概率估计值Table 5 The jump spillover probabilities from U.S.futures markets to Chinese markets

2)美国对中国期货市场跳跃溢出强度的测度结果

表6给出了美国期货同步和异步交易市场对中国期货市场的跳跃溢出强度.跳跃溢出强度的零假设为估计的跳跃溢出等于完全独立时不同期货市场的跳跃溢出,在这一零假设下,两个市场发生跳跃溢出的强度可估计为单一市场潜在跳跃强度的乘积14在零假设下,跳跃溢出强度和跳跃溢出概率是随机的.本文用解靴带法以非常高的置信度测试了跳跃溢出强度[34]..实证结果显示,美国期货同步和异步交易市场对中国期货市场的跳跃溢出强度还是比较大的,且均在5%的水平下统计显著.从样本的估计结果看,美国期货市场的同步交易对中国期货市场的溢出强度明显大于美国异步交易对中国期货市场的溢出强度.无论对Globex电子交易市场还是对正规交易市场而言,美国铜期货市场对中国铜期货市场的跳跃溢出强度显著大于美国大豆期货市场对中国大豆期货市场的跳跃溢出强度.并且,与中国加入WTO过渡期间相比,过渡期后美国期货市场对中国期货市场的跳跃溢出强度明显增强了.此外,还发现中国期货市场对来自美国同步交易和异步交易市场跳跃风险的溢出强度也均存在杠杆效应.另外,如果取溢出强度的倒数作为溢出频度的话,将自然发现过渡期后美国期货市场跳跃风险对中国期货市场的溢出频度明显大于过渡期间,且铜期货市场的溢出频度远大于大豆期货市场.

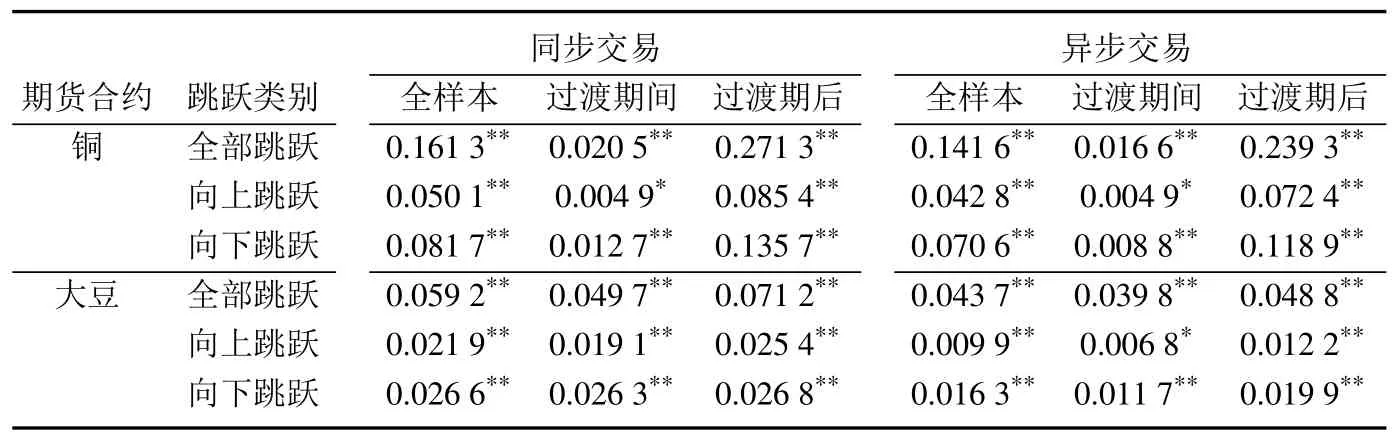
表6 美国期货市场对中国市场的跳跃溢出强度估计值Table 6 The jump spillover intensities from U.S.futures markets to Chinese markets

3)美国对中国期货市场跳跃溢出大小的测度结果

表7给出了美国期货市场对中国期货市场跳跃溢出大小的测度结果.实证结果发现,无论对铜期货市场还是对大豆期货市场而言,美国期货市场对中国期货市场的跳跃溢出大小均为负值.从跳跃幅度上看,美国期货同步交易市场对中国期货市场的跳跃溢出幅度大于美国期货异步交易市场对中国期货市场的跳跃溢出幅度.并且,与中国加入WTO过渡期间相比,过渡期后美国期货市场对中国期货市场的跳跃溢出幅度显然增大了,这一结论与前文跳跃溢出概率和跳跃溢出强度的结论基本一致.这意味着,过渡期后美国期货市场的跳跃风险对中国期货市场的影响显然增强了.此外,通过比较向上跳跃和向下跳跃的溢出大小,不难发现美国期货市场的坏消息对中国期货市场的跳跃溢出大小要大于好消息对中国期货市场的跳跃溢出大小,这进一步给出了美国期货市场对中国期货市场的跳跃溢出往往是由不寻常的坏消息所引起的证据.

4.3 美国期货市场跳跃风险对中国期货市场影响的投资价值实证分析

既然美国期货市场的跳跃风险对中国期货市场具体显著的冲击效应,那么,美国期货市场跳跃风险对中国期货市场产生影响的风险绩效到底如何,尚需进一步探讨.为此,下文将从过滤跳跃前(即存在跳跃因素)和过滤跳跃后(即去除跳跃因素)两种状态来研究中国期货市场受美国期货市场跳跃风险冲击的风险绩效.并且,本文对风险绩效的评价主要从两个方面来考察：一是研究美国期货市场对中国期货市场的跳跃风险溢出贡献度,二是分析美国期货市场的跳跃风险对中国期货组合的夏普比率的影响.

1)美国期货市场对中国期货市场的跳跃风险溢出贡献度分析

既然美国期货市场跳跃风险对中国期货市场的影响是不可忽视的,那么,美国期货市场的跳跃风险对中国期货市场的溢出会达到何种程度呢?为此,本文利用跳跃风险溢出贡献度指标对美国期货市场对中国期货市场的跳跃风险溢出贡献度进行了计算(如表8所示).研究发现,美国期货市场跳跃风险对中国期货市场的溢出是相当大的,从全样本的估计值看,变动范围为16.48%∼65.96%;更具体地,铜期货同步交易市场为65.96%,异步交易市场为36.98%,而大豆期货同步交易市场为46.38%,异步交易市场为16.48%,通过比较同步交易市场和异步交易市场的风险溢出贡献度来看,同步交易市场的风险溢出程度明显大于异步交易市场的风险溢出程度.相对而言,加入WTO过渡期后美国期货市场的跳跃风险对中国期货市场的溢出程度远大于过渡期间美国期货市场的跳跃风险对中国期货市场的溢出程度.并且,美国期货市场向下跳跃的风险对中国期货市场的风险贡献度也显著大于向上跳跃的风险对中国期货市场的风险贡献度,这表明美国期货市场的跳跃风险对中国期货市场的风险溢出贡献度也具有杠杆效应.

表8 美国期货市场对中国市场跳跃风险溢出贡献度的估计值Table 8 The contribution of jump risk spillovers from U.S.futures markets to Chinese marketss

2)美国期货市场跳跃风险对中国期货组合夏普比率的影响分析

下面,将检测美国期货市场跳跃风险溢出的存在是否会导致中国期货组合分散化收益的下降,分散化组合收益本文将用夏普比率来衡量15与Jobson等[31],Li等[35]及Cheung等[29]的研究类似,本文估计分散化收益的方法也将采用夏普比率..由于期货组合综合了更多信息,含有跳跃溢出的分散化组合收益很可能会降低.为此,下文来检测这一结论是否成立,以探讨美国期货市场的跳跃风险在中国期货组合风险绩效中的作用.

在计算过滤跳跃前后的夏普比率之前,先进行无风险利率的选择.本文的无风险利率主要选择3月,6月和1年期人民币定期存款每日基准利率.由于随着时间的变化中国人民银行会对利率做出调整,本文选择2002年1月2日至2010年12月31日一年期国债的均值作为对应期限无风险利率的代表16数据来源于中国人民银行和Wind数据库..表9给出了过滤跳跃前后中国期货组合的夏普比率估计值17事实上,本文也分别对铜和大豆期货市场进行了类似分析,实证研究结论与资产组合的研究结论基本一致.但相对而言,过滤跳跃前的夏普比率值要远小于过滤跳跃后的夏普比率值,且统计性测试也是显著的..在研究中,本文估计了基于不同无风险利率的夏普比率,发现实证结果能有效描绘不同无风险利率下的有效前沿,这意味着这一方法可以用于解决不同风险厌恶的投资者进行最优投资前沿的选择问题.因此,能够通过计算夏普比率及其显著性来探知不同程度的风险厌恶投资者所面临的分散化收益.由表9可知,与不含跳跃溢出的资产组合相比,含有跳跃溢出的分散化收益明显减少了,且对不同的无风险利率而言,均在1%的置信度下统计显著.这说明来自美国期货市场的大量跳跃溢出风险,加大了中国期货市场的风险,从而降低了中国期货市场的夏普比率.另外,通过比较加入WTO过渡期间和过渡期后的夏普比率可以发现：在过滤跳跃之前,过渡期后期货组合的夏普比率明显小于过渡期间期货组合的夏普比率;在过滤跳跃之后,过渡期后期货组合的夏普比率却大于过渡期间期货组合的夏普比率.由此说明,中国经济全面开放后,美国期货市场的跳跃风险对中国期货市场的影响要非常巨大的,绝不可忽视.并且我们还发现,无论对过渡期前还是过渡期后,无风险利率越高,期货组合的分散化收益越小.这说明交易成本越高,中国期货组合的分散化收益越低.由此看来,美国期货市场的跳跃风险的确显著降低了中国期货市场的组合分散化收益,且这一跳跃风险的影响是非常大的,是市场组合所无法规避的,多属于系统性风险18资产组合中跳跃风险往往是系统风险的论证和测度过程可以参见Dunham等[36]..

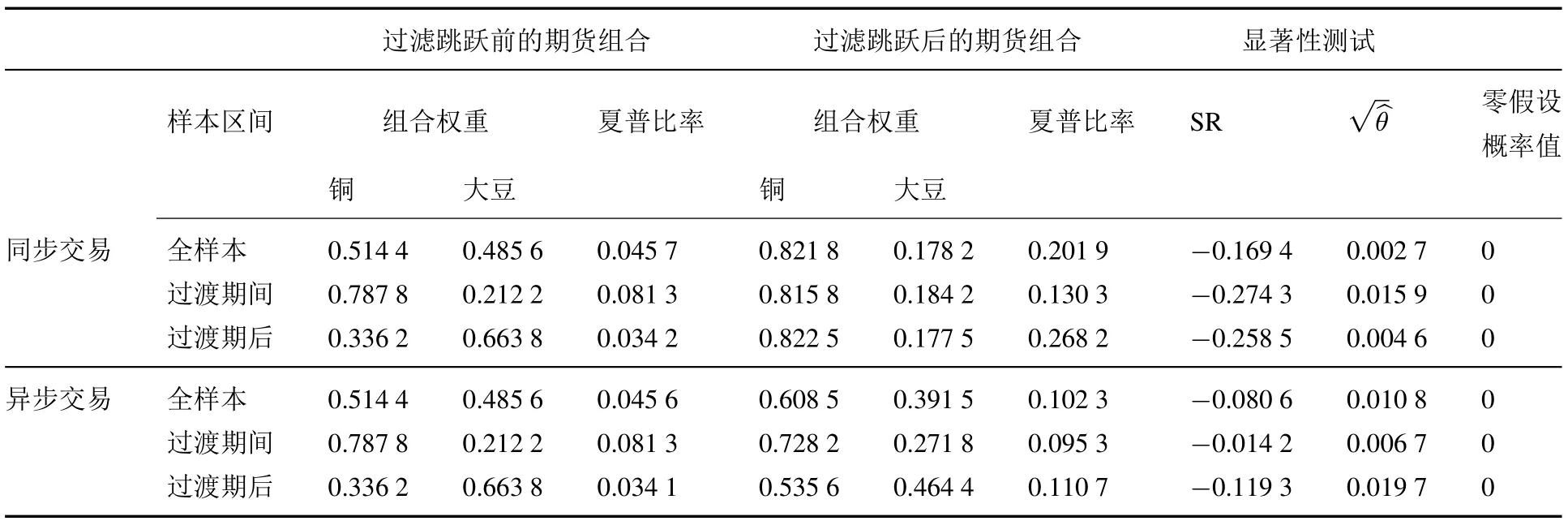
表9 过滤跳跃前后中国期货组合的夏普比率估计值Table 9 The Sharpe ratios of Chinese futures portfolio before and after f i ltering jumps

3)美国期货跳跃风险对中国期货的跳跃风险溢价分析

表10给出了美国期货跳跃风险对中国期货的跳跃风险溢价估计值.研究结果发现,无论对同步交易还是对异步交易的全样本而言,美国期货跳跃风险对中国期货的跳跃风险溢价系数均在1%的水平下统计显著,且数值均为负值,这表明美国期货市场的跳跃风险对中国期货市场的风险溢价具有显著的负向影响;相对而言,大豆期货市场的跳跃风险溢价要大于铜期货市场.通过比较同步交易和异步交易的跳跃风险溢价值可以发现,铜期货市场的同步交易的跳跃风险溢价绝对值要大于非同步交易的绝对值,而大豆期货市场正好与此相反.此外,通过比较加入WTO过渡期间和过渡期后的跳跃风险溢价绝对值发现,对铜和大豆期货市场而言,过渡期后的跳跃风险溢价绝对值要大于过渡期间的绝对值,这意味着过渡期结束后,美国期货市场对中国期货市场的跳跃风险溢价明显增强了.顺便提及美国期货跳跃风险对中国期货的非跳跃风险溢价(全样本)系数也在5%的水平下显著为负值,这说明不受美国跳跃风险影响的中国期货市场的风险溢价也是存在的,其主要原因可归结为中国期货市场本身存在的不受美国期货跳跃风险影响的跳跃成分,虽然非跳跃不存在显著的风险溢价19利用类似的方法,作者对中国期货市场的跳跃风险溢价和非跳跃风险溢价进行了研究,发现我国期货市场存在跳跃风险溢价,而不存在非跳跃风险溢价,这一结果与Chan等[26]对股指期货的跳跃风险溢价结果相一致..

表10 美国期货对中国的跳跃风险溢价估计值Table 10 The jump risk premium from U.S.futures to Chinese futures

表11 美国期货跳跃风险对中国上跳和下跳的风险溢价估计值Table 11 The risk premium of jumping up and down from U.S.futures to Chinese futures

既然美国期货跳跃风险对中国期货市场存在跳跃风险溢价,那么,好消息影响下的上跳跃和坏消息影响下的下跳的风险溢价是否均存在?如果存在,是否具有非对称性?为此,表11给出了美国期货跳跃风险对中国期货市场的上跳和下跳的风险溢价估计值.研究结果发现,上跳和下跳溢价参数和均在5%的水下统计显著;并且,铜期货市场下跳的溢价参数绝对值要大于下跳的溢价参数,而大豆期货市场则相反,这意味着期货市场的上跳和下跳风险溢价是非对称的;具体而言,铜期货市场具有杠杆效应,而大豆期货市场具有反杠杆效应.

5 结束语

为检测美国期货市场的跳跃风险对中国的外溢效应及其投资价值,从同步交易和异步交易视角出发,采用波动跳跃溢出概率,波动跳跃溢出强度,波动跳跃溢出大小,波动跳跃溢出贡献度以及跳跃溢出前后的夏普比率模型对2002年1月2日∼2010年12月31日美中的铜和大豆期货市场进行了实证研究.实证结果表明：

第一,期货市场的跳跃呈现出稀疏性,非对称性和高波动时期下的集聚效应;过滤跳跃前美国(同步和异步)和中国期货市场之间的相关度明显大于过滤跳跃之后,这说明跳跃的存在强化了美中期货市场之间的相依关系.并且,与过渡期间相比,过渡期后美中期货市场之间的相关度要明显大于过渡期间的相关度.

第二,美国期货市场的跳跃风险对中国的影响不仅是显著的，且美国期货同步交易对中国期货的影响明显大于美国期货异步交易对中国市场的影响.相对地，无论在同步还是异步交易市场,美国铜期货的跳跃风险对中国铜期货的冲击能力均大于美国大豆期货市场.此外，美国期货对中国期货的跳跃溢出大小均为负,且美国期货同步交易对中国期货的跳跃溢出幅度也大于美国期货异步交易市场20本文认为美国期货同步交易的跳跃风险对中国期货的影响大于其异步交易的跳跃风险,这一结论与Liu等[1]对中美期货市场关系的结论是不同的.之所以存在这一差异,主要是因为跳跃信息的传递速度往往更快,其影响力度往往更大[37,38]..

第三,过渡期后的美国期货的跳跃风险对中国期货的冲击能力均比过渡期间增强,说明中国经济全面开放以后,中国期货市场与国际市场更加接轨,受到来自美国期货市场的冲击明显加大.并且,美国期货的跳跃风险对中国期货的冲击概率,冲击强度及冲击大小均具有杠杆效应.

第四,过滤跳跃后的期货组合夏普比率明显高于过滤跳跃前的夏普比率;相对地,在过滤跳跃之前过渡期后期货组合的夏普比率明显小于过渡期间期货组合的夏普比率,而在过滤跳跃之后过渡期后期货组合的夏普比率却大于过渡期间期货组合的夏普比率.这意味着来自美国期货市场的大量跳跃溢出风险的确显著降低了中国期货市场的组合分散化收益,且这一跳跃风险往往在期货组合中充当非常重要的角色,是市场组合所无法规避的,多属于系统性风险.

第五,美国期货的跳跃风险溢价对中国具有显著的负向影响;相对而言,大豆期货市场的跳跃风险溢价要大于铜期货市场.并且,铜期货市场的同步交易的跳跃风险溢价绝对值要大于非同步交易的绝对值,而大豆期货市场正好与此相反.过渡期后的跳跃风险溢价绝对值要大于过渡期间的绝对值,这意味着过渡期结束后,美国期货市场对中国的跳跃风险溢价具有明显增强的态势.此外,期货市场的上跳和下跳风险溢价也是非对称的,铜期货市场具有杠杆效应,而大豆期货市场具有反杠杆效应.

参考文献:

[1]Liu Q,An Y.Information transmission in informationally linked markets：Evidence from US and Chinese commodity futures markets.Journal of International Money and Finance,2011,30(5)：778—795.

[2]Neftci S N.An Introduction to the Mathematics of Financial Derivatives.Second Edition.New York：Academic Press,2004.

[3]Easley D,O’Hara M.Price,trade size,and information in securities markets.Journal of Financial Economics,1987,19(1)：69—90.

[4]Mizrach B.Jump and Cojump Risk in Subprime Home Equity Derivatives.Rutgers University,January 2009.

[5]Bittlingmayer G.Output,stock volatility and political uncertainty in a natural experiment：Germany,1880—1940.Journal of Finance,1998,53(6)：2243—2257.

[6]Chan Y,Wei J.Political risk and stock price volatility：The case of Hong Kong.Pacif i c Basin Finance Journal,1996,4(2/3)：259—275.

[7]Cutler D,Poterba J,Summers L.What moves stock prices.Journal of Portfolio Management,1989,15(3)：4—12.

[8]Franck R,Krausz M.Institutional changes,wars and stock market risk in an emerging economy：Evidence from the Israeli Stock Exchange,1945—1960.Cliometrica,2009,3(2)：141—164.

[9]Kim H Y,Mei J P.What makes the stock market jump：An analysis of political risk on Hong Kong stock returns.Journal of International Money and Finance,2001,20(7)：1003—1016.

[10]Asgharian H.Bengtsson C.Jump spillover in international equity markets.Journal of Financial Econometrics,2006,4(2)：167—203.

[11]Duff i e D,Pan J,Singleton K.Transform analysis and asset pricing for aff i ne jump-diffusions.Econometrica,2000,68(6)：1343—1376.

[12]Eraker B,Johannes M,Polson N.The impact of jumps in volatility and returns.Journal of Finance,2003,58(3)：1269—1300.

[13]De Bandt O,Hartmann P.Systemic Risk：A survey.Working Paper,European Central Bank,2000.

[14]刘庆富,许友传.国内外异步期货交易市场之间的跳跃溢出行为：基于风险事件的视角.系统工程理论与实践,2011,31(4)：679—690.Liu Q F,Xu Y C.Jump spillovers between domestic and overseas no-cynchronous futures markets：Based on the perspective of risk events.Systems Engineering：Theory&Practice,2011,31(4)：679—690.(in Chinese)

[15]Chen A H,Siems T F.The effects of terrorism on global capital markets.Europen Journal of Political Economy,2004,20：349—366.

[16]Pindyck R S,Wang N.The economic and policy consequences of catastrophes.Working Paper,MIT Sloan School,2009.

[17]Jarrow R A,Rosenfeld E R.Jump risks and intertemporal capital asset pricing model.Journal of Business,1984,57(3)：337—351.

[18]Ball C A,Torous W N.On jumps in common stock prices and their impact on call option pricing.Journal of Finance,1985,40(1)：155—173.

[19]Wu L.Jumps and dynamic asset allocation.Review of Quantitative Finance and Accounting,2003,20(3)：207—243.

[20]Kurmann M.Dynamic jump risk and portfolio allocation.Working Paper,University of Lausanne,2009.

[21]Liu Q,Tu A H.Jump spillovers in energy futures markets：Implications for diversif i cation benef i ts.Energy Economics,2012(5)：1447—1464.

[22]Wright J H,Zhou H.Bond risk premia and realized jump risk.Journal of Banking and Finance,2009,33(2)：2333—2345.

[23]Broadie M,Chernov M,Johannes M.Model specif i cation and risk premia：Evidence from futures options.Journal of Finance,2007,62(3)：1453—1490.

[24]Todorov V.Variance risk premium dynamics：The role of jumps.Review of Financial Studies,2010,23(1)：345—383.

[25]Todorov V,Bollerslev T.Jumps and betas a new framework for disentangling and estimating systematic risks.Journal of Econometrics,2010,157(2)：220—235.

[26]Chan W H,Feng L.Time-varying jump risk premia in stock index futures returns.Journal of Futures Markets,2012,32(7)：639—659.

[27]Masood O,Sergi B S.How political risks and events have inf l uenced Pakistan’s stock markets from 1947 to the present.International Journal of Economic Policy in Emerging Economies,2008,1(4)：427—444.

[28]Lobo B J.Jump risk in the U.S.stock market：Evidence using political information.Review of Financial Economics,1999,8(2)：149—163.

[29]Cheung C S,Miu P.Diversif i cation benef i ts of commodity futures.Journal of International Financial Markets,Institutions&Money,2010,20(5)：451—474.

[30]Eraker B.Do stock prices and volatility jump：Reconciling evidence from spot and option prices.Journal of Finance,2004,59(3)：1367—1403.

[31]Jobson J D,Korkie B M.Performance hypothesis testing with the Sharpe and Treynor measure.Journal of Finance,1981,36(4)：889—908.

[32]夏 天,程细玉.国内外期货价格与国产现货价格动态关系的研究——基于DCE和CBOT大豆期货市场与国产大豆市场的实证分析.金融研究,2006,(2)：110—117.Xia T,Cheng X Y.The dynamix relationships between Chinese spot’s price and world futures price：Evidence from DCE and CBOT futures and domestic spot soybean markets.Journal of Financial Research,2006,(2)：110—117.(in Chinese)

[33]华仁海,刘庆富.国内外期货市场之间的波动溢出效应研究.世界经济,2007,(6)：64—74.Hua R H,Liu Q F.The volatility spillovers between domestic and overseas futures markets.Journal of World Economy,2007,(6)：64—74.(in Chinese)

[34]Hogg R,Tanis E.Probability and Statistical Inference.6th ed.Englewood Cliffs：Prentice Hall,2001.

[35]Li K,Sarkar A,Wang Z.Diversif i cation benef i t of emerging markets subject to portfolio constraints.Journal of Empirical Finance,2003,10(1/2)：57—80.

[36]Dunham L M,Friesen G C.An empirical examination of jump risk in U.S.equity and bond markets.North American Actuarial Journal,2007,11(4)：76—91.

[37]Dungey M,Hvozdyk L.Cojumping：Evidence from the US treasury bond and futures markets.Journal of Banking and Finance,2012,36(5)：1563—1575.

[38]徐元栋.投资者的奈特不确定性情绪与股市巨幅波动.系统工程学报,2015,30(6)：736—745.Xu Y D.Knightian uncertainty emotion of investors and the huge f l uctuations of stock market.Journal of Systems Engineering,2015,30(6)：736—745.(in Chinese)