基于有限元理论的竖曲线段吊弦计算方法

郑 伟，吴铁成



基于有限元理论的竖曲线段吊弦计算方法

郑 伟，吴铁成

基于有限元理论对竖曲线段整体吊弦的计算方法进行阐述，并对该方法进行数据验证，以实现整体吊弦的精确计算。

接触网；有限元；吊弦计算；竖曲线

0 引言

接触网整体吊弦的计算方法从最初的抛物线计算法发展到今天的有限元计算法，计算理论日趋复杂和精细。受线路条件水平区间和竖曲线变化的影响，整体吊弦的计算容易出现偏差，为实现整体吊弦的精确计算，需找到一种适应有限元计算理论且在竖曲线段也具有较高精度的计算方法。本文将利用闽赣客专的基础数据，基于有限元计算法，对竖曲线段的吊弦计算方法进行阐述，并对结果进行对比分析，验证竖曲线段参数修正方法的正确性，以实现整体吊弦的精确计算。

1 计算模型

1.1 竖曲线模型

在铁路接触网工程施工中，线路竖曲线参数一般为给定的设计参数，其数量较多，吊弦计算使用的主要参数为变坡点里程、切线段长度、斜率、半径。闽赣客专竖曲线主要参数如表1所示。

表1 线路竖曲线主要参数

为便于理解和观察，根据参数绘制出的竖曲线模型如图1所示。

1.2 参数修正

在整体吊弦计算中，竖曲线主要影响接触网的承力索高度和接触线高度，因此在进行基于有限元法计算前，需将承力索高度和接触线高度修正到竖曲线所在的高程系内。为便于计算，一般以所计算锚段内的第1根支柱为起点重新设置高程系，而不使用现场实际高程。

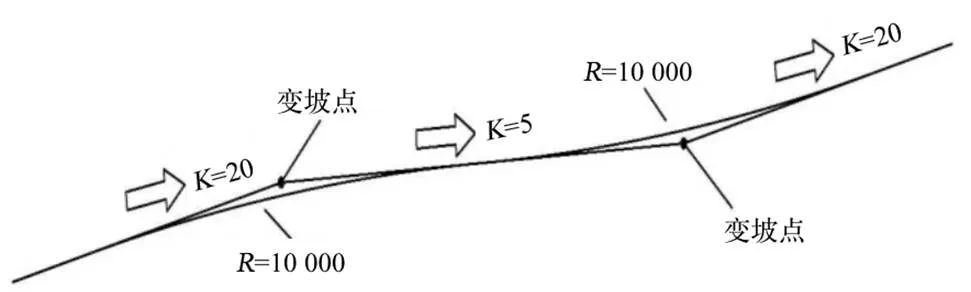
图1 竖曲线模型

1.2.1 接触线高度修正

建立接触线高度修正模型如图2所示。以锚段内接触线定位点为起点，高程设为0，计算定位点和吊弦点接触线高度相对高程系的偏差，接触线高度与偏差之和为接触线在高程系内的高程。

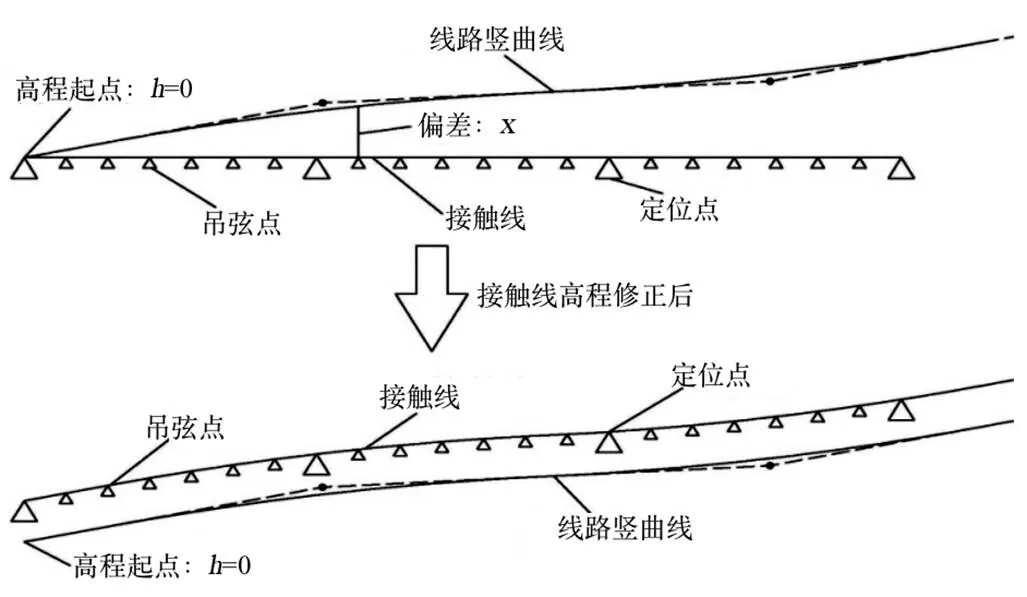
图2 接触线高度修正模型

设接触线修正点距离起点里程为x，变坡点里程为，斜率为，变坡点半径为，切线长为，修正点相对地点偏差为，接触线定位点、吊弦点实测高度为，接触线定位点、吊弦点高程系内高度为x。

上坡或下坡段偏差计算式为

=x·（1）

圆弧段偏差计算式为

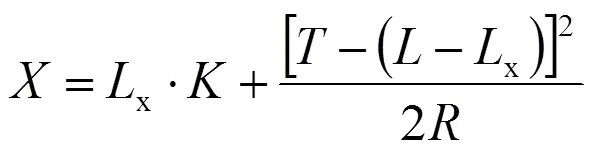
接触线高程修正计算为

x=+（3）

1.2.2 承力索高度修正

根据接触线高度修正理论，进行类比分析，可以知道，在进行承力索高度修正时，需计算出承力索定位点处相对高程系的偏差，承力索高度与偏差之和为承力索在高程系内的高程。修正计算式同接触线参数修正计算式一致，修正模型如图3所示。

图3 承力索高度修正模型

1.3 吊弦计算

1.3.1 建立吊弦计算模型

利用有限元法计算时，主要求在承力索自重和接触线、吊弦等负载作用力下承力索在吊弦安装点的位移，然后利用高程减去位移和接触线高度，便可得到吊弦的长度，计算模型如图4所示。

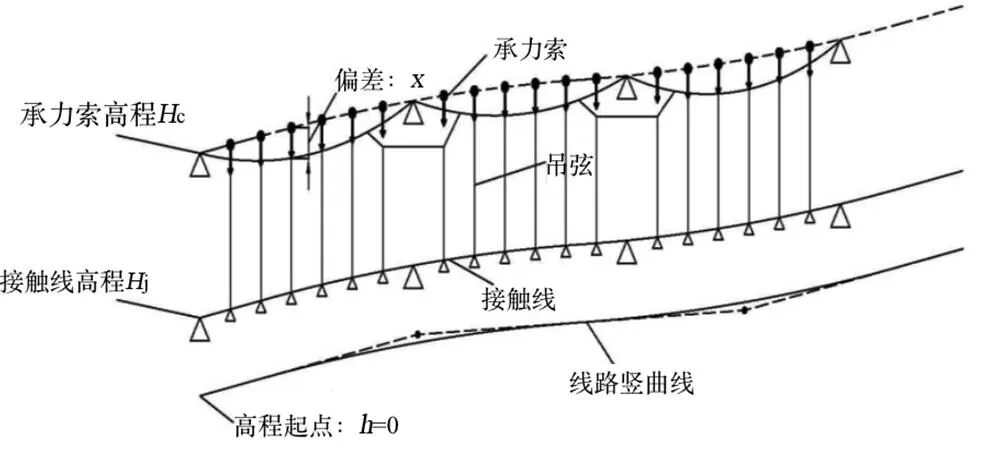
图4 吊弦计算模型

1.3.2 吊弦计算式

根据吊弦计算模型可以得出，经过有限元法的求解，可以得出承力索在高程系内吊弦点处的位移量，接触线在高程系内的高程为j，可得整体吊弦的长度为

d=c-j-（4）

式中，c为高程系内承力索高度；j为高程系内接触线高度；为承力索在高程系内的位移量。

2 计算理论验证

为验证竖曲线内吊弦计算理论的正确性与准确性，选取闽赣客专的1锚段中的中间跨（DK616+601.22—DK 617+820.86）进行计算验证，接触网张力为（30+21）kN，吊弦计算参数如表2所示。

表2 1锚段吊弦计算参数

为验证计算的正确性，与该锚段内对应的线路参数进行核对，并验证该锚段仅处于竖曲线段内，不存在水平曲线的影响。竖曲线资料如表3所示。

表3 1锚段所在竖曲线参数

在计算前，首先建立以780支柱为0点高程的高程系，并通过计算承力索定位点、接触线定位点和吊弦点相对高程系的偏差，分别对1锚段接触线高度、承力索高度进行了修正，之后利用有限元法计算出承力索吊弦点位移量，利用式（4）计算得出该锚段吊弦长度，如表4所示。

表4 1锚段吊弦计算结果 m

选取其中任意3跨与已知吊弦长度进行对比，为便于观察，将误差定义在mm级，其对比结果如表5所示。

对比计算结果可以看到，利用该竖曲线计算方法得到的整体吊弦长度的误差均在±1mm范围内。经查用于该客专工程的计算软件已用于多条客专线路，同时经过现场的安装验证，原已知吊弦数据可靠、精确。

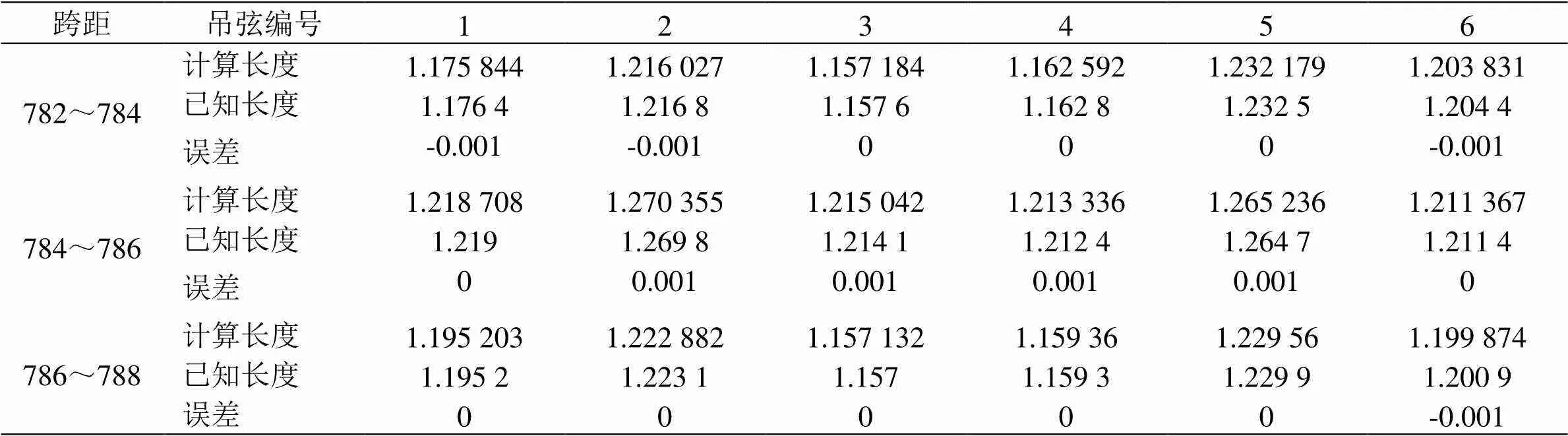
表5 吊弦计算结果对比 m

3 结语

基于有限元计算理论的竖曲线段吊弦计算方法，在利用有限元计算整体吊弦计算前，将竖曲线段的承力索与接触线高度参数修正到竖曲线所在的高程系内，再进行整体吊弦计算。由计算结果的验证可以看到，该方法得到的计算结果误差较小，精确性较高，能实现整体吊弦的精确计算，可用于实际工程。

[1]阮杰，颜伏伍，李红梅. 电气化高速铁路接触网静态模型的建立[J]. 铁道学报，2012，34（8）：20-25.

[2] 李瑞平，周宁，梅桂明，张卫华，等. 初始平衡状态的接触网有限元模型[J]. 西南交通大学学报，2009，44（5）：732-737.

[3] 刘大勇，吴积钦. 基于索网找形的吊弦长度计算方法探讨[J]. 电气化铁道，2008（4）：31-33.

[4] 常丽，李丰良，年晓红. 武广高铁定位器坡度算法研究[J]. 铁道科学与工程学报，2014，11（2）：131-135.

[5] 冯超，韩俊杰，苗杰，等. 基于有限元方法的接触网吊弦长度计算[J]. 电气化铁道，2012，23（4）：1-4.

The finite element theory based method for calculation of integral droppers in vertical curve section is illustrated, and the data verification is made by this method accordingly, so as to realize the accurate calculation of integral droppers.

OCS; finite element; calculation of droppers; vertical curve

U225.4+8

B

1007-936X(2018)02-0047-03

2017-08-01

10.19587/j.cnki.1007-936x.2018.02.012

郑 伟.中铁电气化局集团西安电气化工程有限公司，工程师；吴铁成.中铁电气化局集团西安电气化工程有限公司，高级工程师。