差压式流量计小流量在线非线性补偿的测量方案
2018-04-26冯杰顾佳乐
冯杰,顾佳乐
(上海石油天然气有限公司 天然气处理厂,上海 201304)
差压式流量计是常用的流量测量仪表。标准孔板的流量系数经Reader-Harris/Gallagher修改,于1998年被采纳作为标准孔板流出系数的计算公式。它对小流量时差压式流量计的补偿提供了理论基础,但在分散控制系统(DCS)中实现有困难,为此,笔者提出两种实施方法: 直接用Reader-Harris/Gallagher公式,但在DCS上Reader-Harris/Gallagher公式实施困难;针对特定标准孔板,用NURBS函数拟合标准孔板流出系数的Reader-Harris/Gallagher计算公式,并在DCS中实现。该方法既解决了小流量在线补偿的实施问题,也提高了差压式流量计的测量范围度和精度。
1 NURBS样条函数
1.1 B样条基函数
B样条即基本样条(basic spline)。1946年由舍恩贝格(Schoenberg)提出,并在1972年由德布尔和考克斯(deBoor-Cox)分别独立给出B样条计算的标准算法[1-2]。理论上常采用截尾幂函数的差商定义B样条曲线,实际应用则常采用B样条的递推定义。
B样条曲线采用控制顶点定义曲线[1-2]。曲线方程可描述为
(2)
式中:Pi——控制多边形的顶点,i=0,1,…,n;Ni,k(u)——k次(k-1次)B样条基函数,i=0,1,…,n。
其中,每个k次规范B样条基函数称为规范B样条,或简称B样条。由于它由非递减节点矢量u的序列T:u0≤u1≤…≤un+k所决定的k次分段多项式,因而,称为k-1次多项式样条。
根据德布尔-考克斯的递推公式,曲线方程可写为
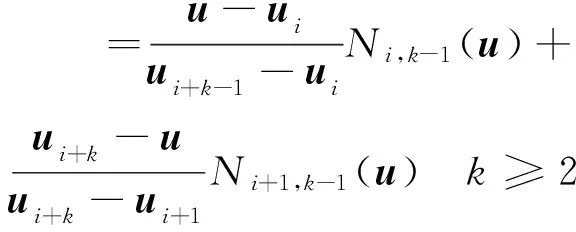
(4)
式中:i,k——下标,i表示序号,k表示次数。
1.2 三次非均匀有理B样条函数
三次非均匀有理B样条函数描述为
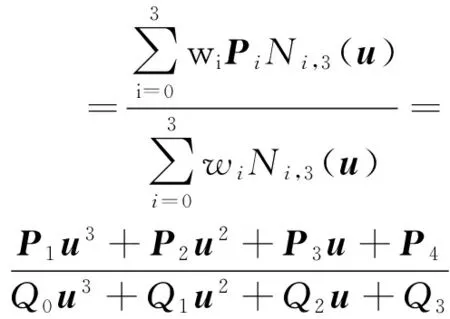
(5)
式中:wi——权因子,分别与控制顶点Pi相联系,(i=0,1,…,n);Ni,k(u)——节点矢量,u=[u0,u1,…,un+k+1]按递推公式确定的k次规范B样条基函数;P1,P2,P3,P4——分子系数,为矢量;Q0,Q1,Q2,Q3——分母系数。B样条基函数的递推公式见式(3)~式(4)。
在数控技术中,NURBS曲线插补算法将定义NURBS曲线的控制顶点、权因子、节点矢量和进给速度等作为NC程序指令,在CNC系统生成NURBS曲线,驱动机床运动,加工出NURBS曲线的形状,这就是NURBS曲线插补。在非线性补偿环节中应用的NURBS曲线,可根据应用要求选用不同的阶次。
2 差压式流量计在非线性补偿中的应用
2.1 差压式流量计的问题
差压式流量计是应用历史最久远的流量计之一[3-4],其测量原理是孔板上游侧与下游侧之间产生的静压差与流过该装置的流体流量之间存在下列关系:
当满足0.2≤β≤0.6时,流出系数C的不确定度为0.5%。其他条件下,不确定度会有所增加。其中,C经Reader-Harris/Gallagher修改,可表示为
C=0.596 1+0.026 1β2-0.216β8+0.000 521×
(0.043+0.080e-10L1-0.123e-7L1)×
(7)
当工艺管道的管道内径D<71.12 mm时,增加下列项:
式中:β——节流孔直径d与D之比,即β=d/D;ReD——根据D和流体流量等数据计算出的雷诺数;L1——孔板上游端面到上游取压口的距离l1除以D得出的商。
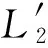
根据Reader-Harris/Gallagher公式,可画出不同管道直径和不同取压方式下,C与ReD,β之间的关系曲面。角接取压,D=150 mm时,C与ReD,β的关系如图1所示。
从图1可见,当D确定后,如果d也确定,则当流体的ReD大于某限值时,其C可基本稳定在某个规定的值。通常在0.60~0.61,而测量不确定度应满足小于0.5%。
角接取压,D大于72.12 mm时,β在0.4~0.5,C与ReD的关系见表1所列。根据表1中数据的分析,可以发现,当最大流量与最小流量之比为10∶1时,即小流量时,其C的误差可达2%。但如果最小雷诺数大于2×104,则C的误差就可小于0.5%。该条件是采用差压式流量计有最小雷诺数限制的原因。由于受到流体流速的限制,最大流量不能设置很大。又由于小流量时,ReD成比例缩小,在C的非线性影响下造成流量测量的精度下降。因而,该情况是差压式流量计的范围度不能较大的原因。其根本原因是在流量小时,ReD也小,这时,C与ReD之间存在较大的非线性关系,造成小流量时流量测量误差大,和流量测量范围度不能大的结果。
解决该类非线性关系的最好方法是进行非线性补偿[6-7]。对差压式流量计由于存在迭代运算,加上在DCS中进行式(7)的运算比较困难,因此,实际应用时可采用两种实现的方法。
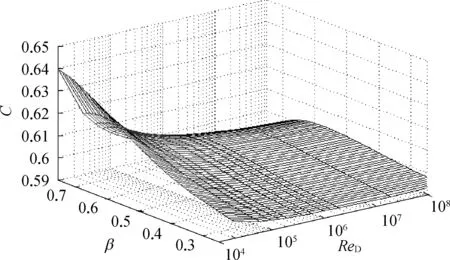
图1 角接取压时C随ReD和β变化示意
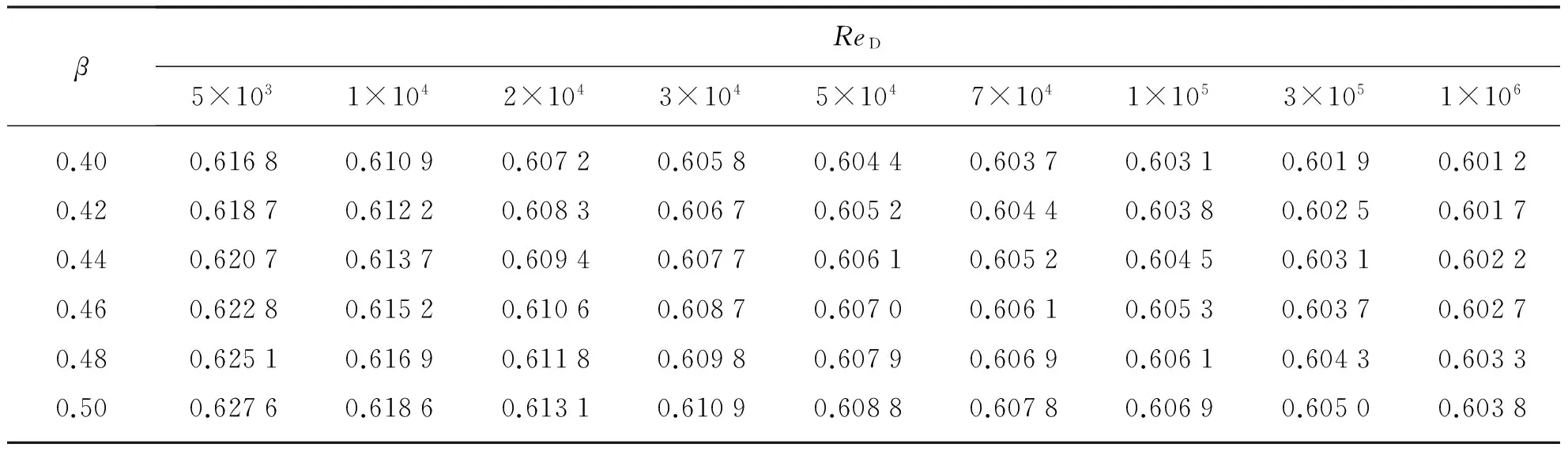
βReD5×1031×1042×1043×1045×1047×1041×1053×1051×1060.400.61680.61090.60720.60580.60440.60370.60310.60190.60120.420.61870.61220.60830.60670.60520.60440.60380.60250.60170.440.62070.61370.60940.60770.60610.60520.60450.60310.60220.460.62280.61520.61060.60870.60700.60610.60530.60370.60270.480.62510.61690.61180.60980.60790.60690.60610.60430.60330.500.62760.61860.61310.61090.60880.60780.60690.60500.6038
2.2 差压式流量计理论补偿方法
当实际差压流量计已安装在工艺管道中时,可采用理论补偿方法。该方法根据Reader-Harris或Gallagher公式,根据已知的β和取压方式,计算出C与ReD之间的关系。根据两者关系,有多种方法实现补偿,如采用多段折线近似法进行补偿;采用拟合函数进行补偿;也可用其他非线性环节实现,例如,神经网络等。
示例是已经安装的某节流装置,已知D=100.00 mm,β=0.40,角接取压方式。为提高拟合精度,取点较多,其计算结果见表2所列。采用NURBS函数进行拟合,其NURBS函数表示为
(10)
式中:p1=3.741×10-13;p2= -6.771×10-8;p3=0.605 6;p4=42.30;p5=0.251 8;p6=0.417 3;q1=-26.05;q2=0.859 9;q3=0.944 8。
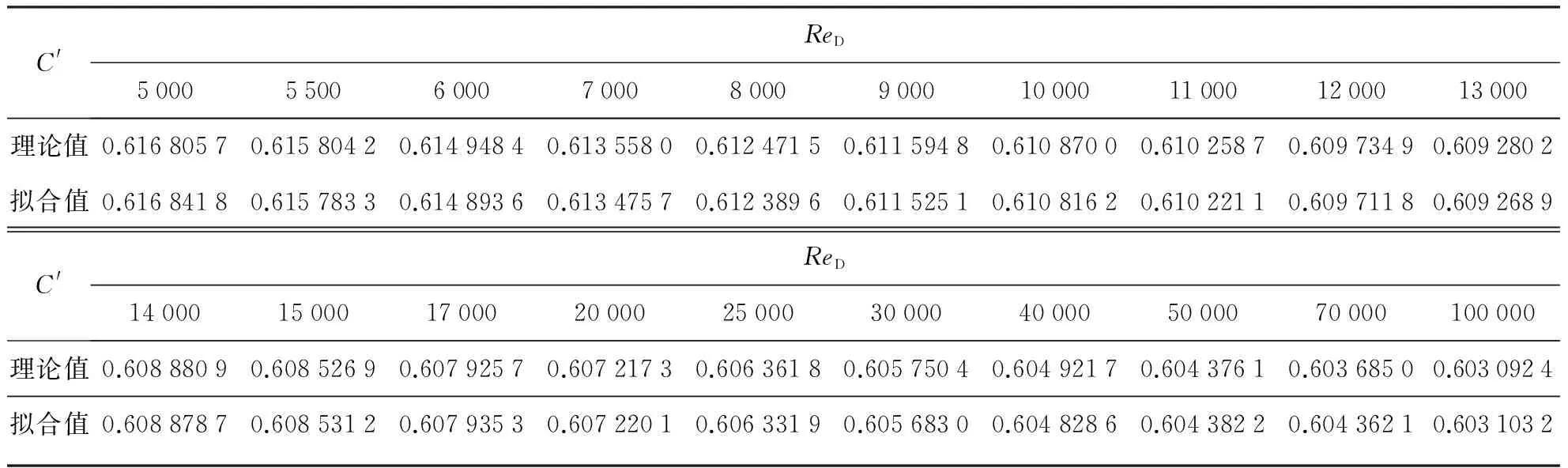
表2 角接取压孔板C′的理论值和拟合值
从表2可见,用式(10)拟合Reader-Harris或Gallagher计算公式,具有很高的精度,最大误差小于0.013%。因此,可直接根据ReD确定C。
2.3 差压式流量计实际标定补偿方法
在新建项目中,可用实流标定的方法确定不同流量时ReD与C的关系曲线,采用上述拟合方法确定其非线性关系。最简单的方法是用多段折线方法拟合,但需设置段数,并用内插方法确定其输出值[8-10]。例如,DCS可以实现其他非线性环节[11],也可采用神经网络实现非线性关系,或用有关方法获得该非线性关系的描述,在此不多述。本文采用NURBS函数拟合在特定径比条件下的ReD与C之间的非线性关系,并实际实施。将NURBS函数表示为下列形式。
利用可编程控制器编程语言中的可重用性,发现NURBS函数的基本算式是y=Ax+B。为此,可编写AXB函数实现。NURBS函数的程序实现如图2所示。
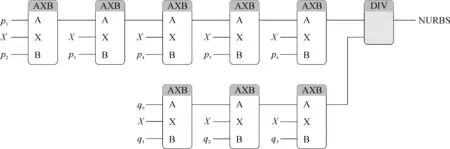
图2 NURBS函数的程序实现流程示意
2.4 DCS中在线非线性补偿关系的实现
为在线实施,先建立Online功能块,用于实现非线性的ReD与C的关系,再针对本文的实际应用,编写主程序,它由QCal,ReCal和NUBRS 3个功能块组成。以C作为反馈变量,该程序为迭代程序。QCal功能块用于计算流体流量,ReCal功能块用于计算ReD,NUBRS函数用于计算不同ReD下的C。
在线实现时,将Online与用常规开方计算的结果进行比较,确定其误差。如图3所示。
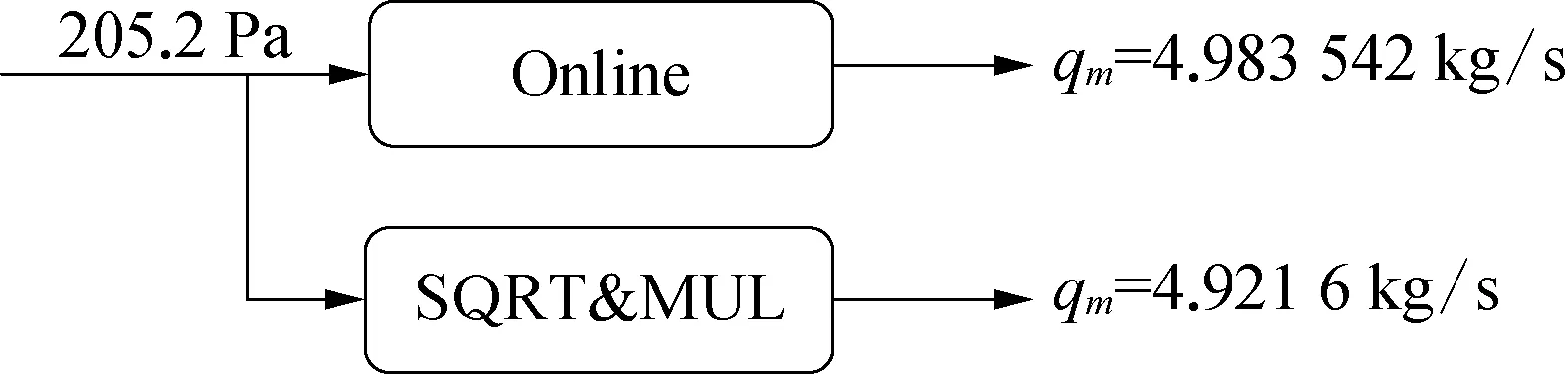
图3 在线运行时的结果显示
从图3可见,当实际差压输入信号是205.2 Pa时,实际流量应为4.983 542 kg/s。如果没有非线性补偿,显示值是4.921 6 kg/s,显示值偏小,误差达1.24%。通过该方法的补偿,使原流量计的范围度提高到接近10∶1。
3 结 论
为提高差压式流量计的流量测量精确度和范围度,可对小流量进行在线非线性补偿。由于标准孔板C的计算公式实现比较复杂,在DCS中计算较困难,因而采用NURBS函数[9]来拟合该非线性关系,并用它计算小流量时的C,通过该非线性补偿的方法,提高了小流量测量精度,同时提高了测量范围度。
参考文献:
[1] Piegl L, Tiller W. The Nurbs Book. [M].2版. 赵罡,穆国旺,王拉柱,译.北京: 清华大学出版社,2010.
[2] 王宁,禹人贵. 非均匀有理B样条曲线的快速实现[J].荷泽学院学报,2009,31(02): 59-61.
[3] 罗健旭,黎冰,黄海燕,等. 过程控制工程[M].3版. 北京: 化学工业出版社,2015.
[4] 周人,何衍庆. 流量测量和控制实用手册[M].北京: 化学工业出版社,2013.
[5] 李明华,彭淑琴,尤竹霖,等.GB/T 2624—2: 2006 用安装在圆形截面管道中的差压测量满管流体流量 第2部分: 孔板[S].北京: 中国标准出版社,2006.
[6] 纪纲. 流量测量仪表应用技巧[M].2版. 北京: 化学工业出版社,2009.
[7] 纪纲,纪波峰. 流量测量系统远程诊断集锦[M].北京: 化学工业出版社,2012.
[8] 何衍庆,姜捷,江艳君,等. 控制系统分析、设计和应用——Matlab语言的应用[M].北京: 化学工业出版社,2003.
[9] 彭瑜,何衍庆. IEC 61131-3编程语言及应用基础[M].北京: 机械工业出版社,2009.
[10] 何衍庆. 常用PLC实用手册[M].北京: 电子工业出版社,2008.
[11] 何衍庆,黄海燕,黎冰. 集散控制系统原理及应用[M].北京: 化学工业出版社,2009.
