水中管道顺流舞动水弹性分析

张大朋，白 勇，刘科伟，朱克强

1.浙江大学建工学院，浙江杭州 310058

2.宁波大学海运学院，浙江宁波 315211

深海石油勘探开发兴起于20世纪70年代末[1]，至今已有30多年的历史。海洋平台上生产的油气要通过管道来输运，由于波流作用，管道受到水动力、惯性力和弹性力的耦合作用而发生运动，这是管道水弹性的体现。

水弹性理论是把液体和固体弹性系统作为一个统一的动力系统来研究它们之间相互作用的理论[2-7]，解决水弹性问题的重要关键是找到流体和固体弹性系统的耦合条件。在水弹性作用过程中，流体的动压力是一种作用于弹性系统的外加载荷，其大小取决于弹性系统振动的位移、速度和加速度；另一方面，流体动压力又会改变弹性系统振动的位移、速度和加速度。这种互相作用表现为流体对于弹性系统在惯性、阻尼和弹性诸方面的耦合现象。由惯性耦合产生附连质量，在有流速场存在的条件下，由阻尼耦合产生附连阻尼，由弹性耦合产生附连刚度。它们取决于流场条件及液体和弹性系统相连接的边界条件，不易求解。本文以海洋中的管道为研究对象，将其简化为一弹性悬臂梁，采用广义坐标法[2]，即将系统的惯性与弹性特性转化到一些振型上去，采用国际水动力分析软件OrcaFlex建立模型[4，7-8]并进行静态分析及动态运算，用Matlab得出管道曲率、运动速度、斯特哈尔数、雷诺数、振动幅度与直径之比和剪切力随时间的变化曲线。

1 基本理论

采用假设模态法，使用有限个假设模态的振动来近似地线性描述弹性体的振动。在梁的振动问题中，设梁的位移（或挠度）可表示为：

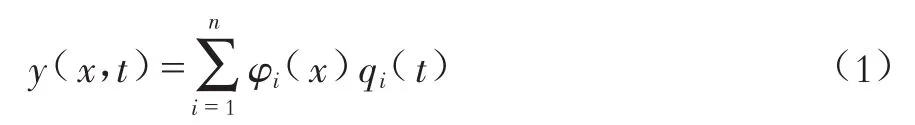
式中：φi（x）为假设模态函数，是指定边值问题的容许函数；qi（t）是相应的广义坐标，单位为m。利用拉格朗日方程，得出关于广义坐标qi（t）的一组（n个）运动微分方程。

梁在振动时的动能T为：

式中：l为梁的总长度，m；ρ（x）在这里指的是梁在某一位置的密度，kg/m3；T为动能，J。

写成矩阵形式有：

在弯曲振动中，梁的势能可表示为：

式中：U为势能，J；EI为弯曲刚度，N·m2。

写成矩阵形式有：

式中：q为广义位移矩阵，m；K为广义刚度矩阵，N/m。且有

由于梁受外部激扰的作用，这时系统已经是非保守的，故拉格朗日方程取如下形式：

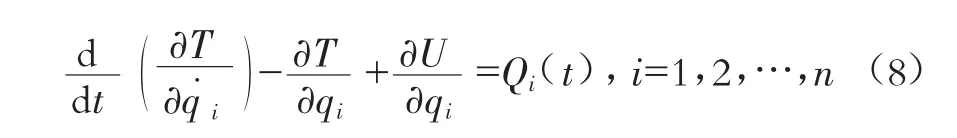
式中：Qi（t）为对应于广义坐标qi的广义力，N。按广义力的定义，激扰力在系统虚位移上所作的虚功就等于各个广义力在虚位移上所作的虚功。由此可求出各个广义力。

设作用在系统上的激扰力可表示为：

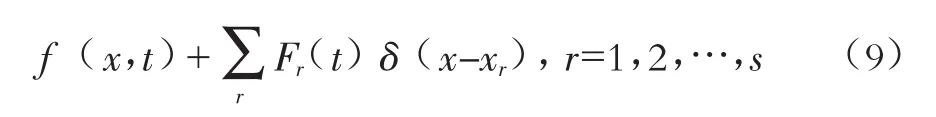
式中：f（x，t）表示分布力，N/m；Fr（t）δ（x-xr）表示作用于xr处的集中力，N；δ（x-xr）是δ函数：

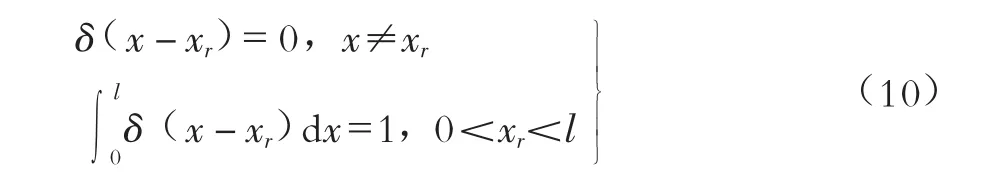
Fr（t）δ（x-xr）的量纲与分布力相同。

由式（1）可知，系统的虚位移可取为：

于是，激扰力在系统虚位移上所作的虚功为：

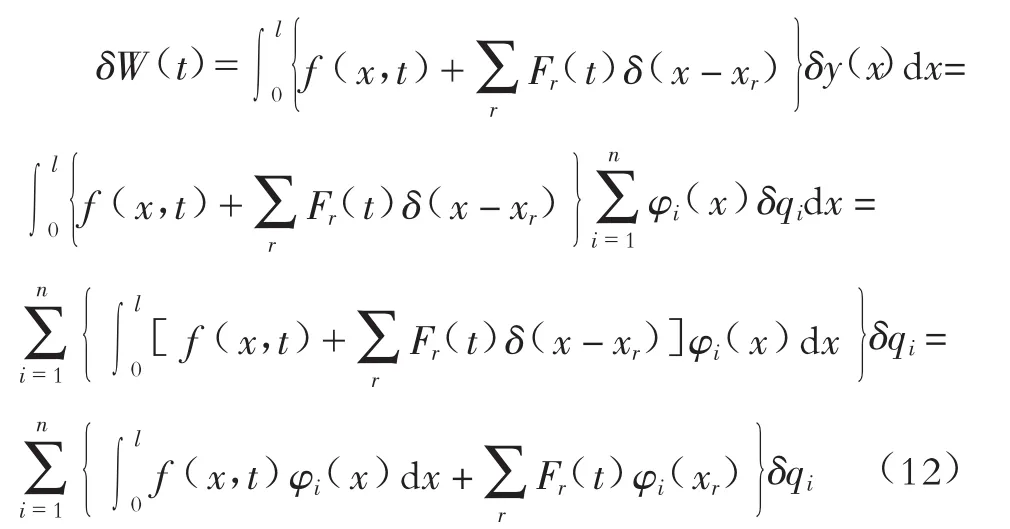
按照广义力的定义，有：

所以有下式：

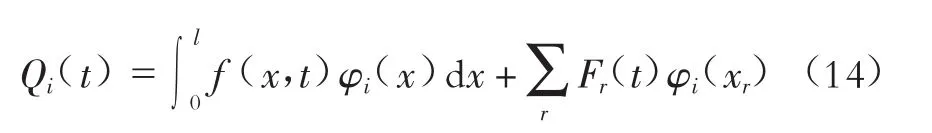
即对应于qi的广义力Qi的表达式。

将式（2）、（5） 和（12） 代入方程（8） 中可得：

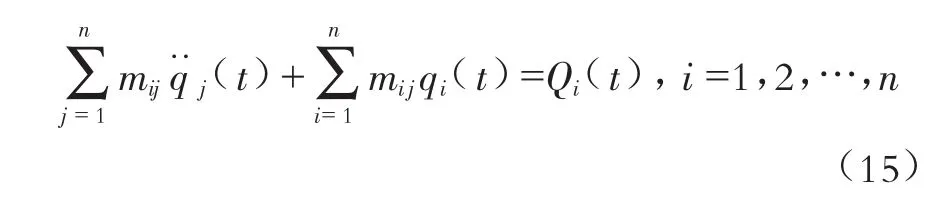
写成矩阵形式为：

2 算例与分析

以横跨海沟的某水下输油管道为例，将其简化为圆柱形，管道模型见图1。模型的几何参数：直径D=0.107 m，长度L=17 m，单位长度质量m=16 kg/m，弯曲刚度为 0.25 kN·m2，轴向刚度为1.05×102kN，扭转刚度为10 kN·m2，阻力系数Cd=1.2，附加质量系数 Cm=1.0，泊松比 0.3，流体密度为 1.024×103kg/m3，运动黏性系数 1.2×10-6m2/s。水流的速度为6 m/s，模拟时间为120 s，计算管道曲率、运动速度、振动幅度与直径之比等在管道和流体耦合过程中的变化。

图1 管道模型示意

模拟开始后，管道曲率、运动速度、振动幅度与直径之比和剪切力的变化，如图2所示。

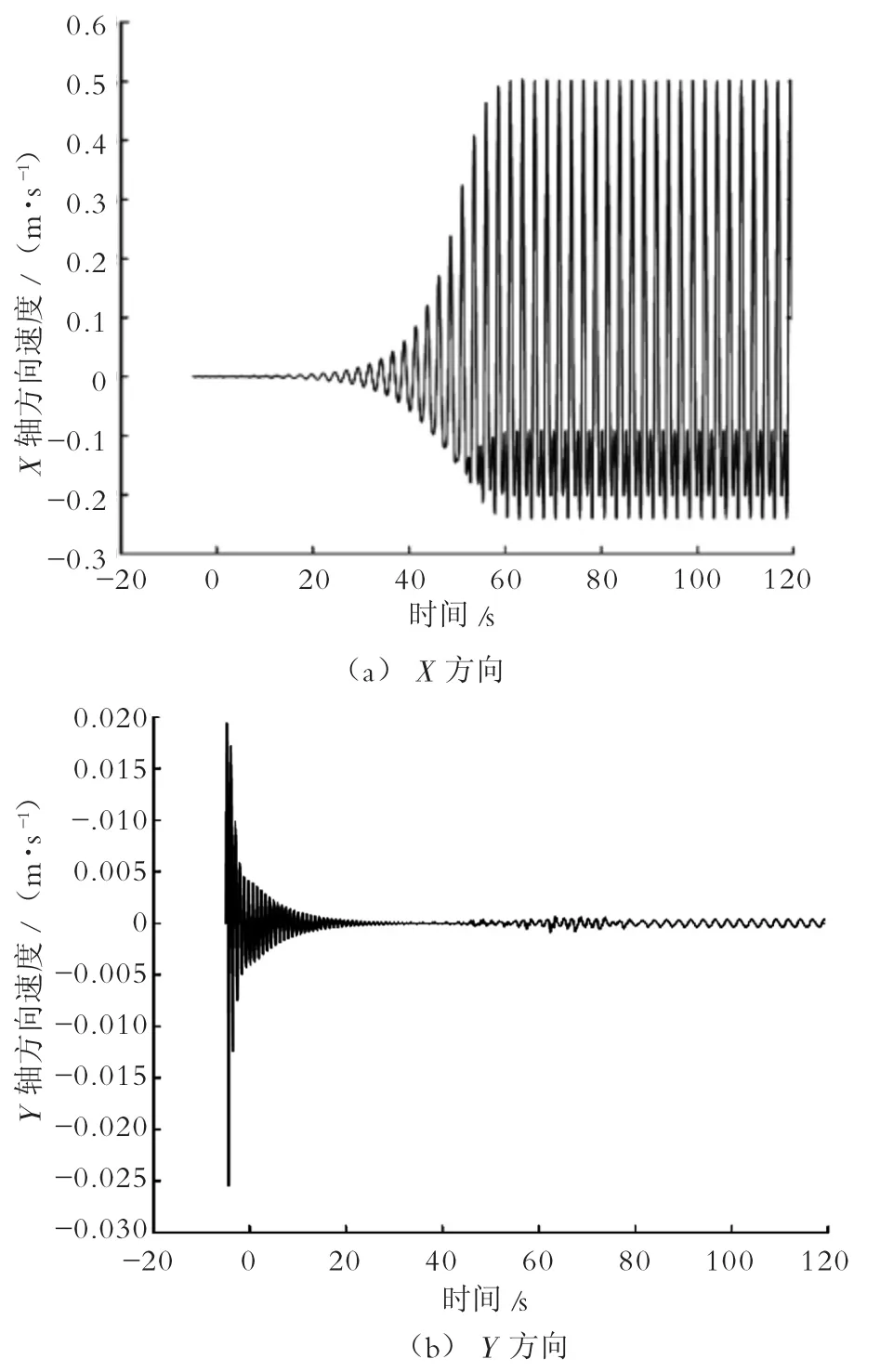
图2 管道速度-时间关系曲线

从图2的管道速度-时间关系曲线可以看出：模拟开始后，在速度为6 m/s的流体的水动力作用下，管道由于流体的作用力变得不稳定，在大约20 s以后，管道右端开始出现明显的振动，且振幅越来越大，最后稳定在一个范围。管道在沿Y轴方向的速度迅速增加到最大，随后逐渐减小，在模拟时间（20 s）以后沿Y轴（速度）在0附近上下浮动（0.002 m/s），大小可以忽略。X轴方向速度在开始时增加缓慢，但在30 s后速度增加，直至在 -0.25 ～ 0.5 m/s范围内变化。

将图3、图4分别与图1进行对比，不难发现在管道的右端尽管运动幅度比左端大，但是管道的曲率半径在左端（0.25～1 m范围内） 的变化比右端大得多。而管道的振动幅度与直径之比的变化却与曲率半径变化相反，管道的左端运动幅度较小，所以横截面无明显变化；管道的右端运动幅度较大，故管道的振动幅度与直径之比变化比较大，在大约14 m处管道横截面变化最大。换句话说，尽管右端比左端运动幅度大，但是由于左端固定，故管道在顺流向发生舞动时，左端的剪切力比右端明显要大。此外，从速度-时间关系曲线上可以发现，管道运动一段时间后，只剩下沿X轴方向的速度，故管道的主运动是在OXZ面内运动。

图3 管道运动过程中曲率随管道长度变化

图4 管道运动过程中管道振动幅度与直径之比随管系长度变化

以上的变化趋势表明管道在顺流向时需要注意以下三点：

（1）管道的弹性模量对顺流向管道的振幅产生影响，若考虑不慎，在大流速情况下，管道会由于持续而猛烈地反复振动而导致管道截面的急剧变化，进而会使连接端的截面产生复杂的变化和径向骤缩，甚至导致管道的连接端直接断裂；同时为了减小管道顺流向的振动，可增加管道的单位浸水重量，使管道埋入海床，减小海流的冲刷。对于与连接端相连的管道段而言，由于曲率变化较大，管道易在反弯点附近受损，因此在此段的设计上应根据曲率变化给予优化。管道的运动会导致管道径向应力和应变的变化，而高频的振动会造成应力过大和管道的失效。

（2）发生以上现象正是由于管道为细长挠性构件，管道与流体相互作用，管道在水流的拖曳作用下顺流舞动，这正是水弹性的体现。

（3）由于管道右端的横截面变化较大，管道在此处也容易折损，在管道设计时应针对性地选取材料，以此综合考虑保障管道的安全可靠性能。

3 结束语

本文采用广义坐标法建立水中管道顺流时的动态响应模型，结合假设模态法利用拉格朗日广义力的平衡方程推导水动力响应的计算公式，并得到了管道振动的控制方程。模拟了水中管道顺流舞动的时间历程，得到了管道在X、Y轴方向的运动速度图，以及整根管道的曲率、横截面变化和管道的运动轨迹，分析了水中管道的结构设计的关键点，可为相关工程实践提供一定的理论参考。

[1]李志刚.深水海底管道铺设技术［M].北京：机械工业出版社，2012：1-5.

[2]季文美，方同，陈松淇.机械振动[M].北京：科学出版社，1985.

[3]罗伯特·E·兰德尔.海洋工程基础[M].包从喜，译.上海：上海交通大学出版社，2001.

[4]ZHU Keqiang，CAI Ying，YU Chunling，et al.Nonlinear hydrodynamic response of marine cable-body system undergoing random dynamic excitation[J].Journal of Hydrodynamics，2009，21（6）：851-855.

[5]朱克强，李道根，李维扬.海洋缆体系统的统一凝集参数时域分析法[J].海洋工程，2002，2（25）：101-103.

[6]张成，刘志忠.水下细长体结构“流—刚—弹耦合”特性及方法[J].舰船科学技术，2014，36（9）：25-31.

[7]董鹏，朱克强，秦道武.海洋平台立管系统的三维动态响应仿真研究[J].港工技术，2011，48（4）：5-7.

[8]朱克强，郑道昌，周江华，等.生产驳船多点系泊定位动态响应[J].中国航海，2007，71（2）：6-9.