基于果蝇算法优化极限学习机的体育竞赛成绩预测研究

张文， 牟艳， 高振兴， 刘志丰

(河海大学物联网工程学院， 江苏常州 213022)

0 引言

根据大型运动会已有的运动成绩对将要发生的体育竞赛成绩进行预测，有助于为运动员、教练员提供训练和竞赛目标的决策依据，同时可以挖掘出体育竞赛运动成绩的发展特征和规律。因此，对体育竞赛成绩进行预测具有重要现实价值和理论意义，其预测精度的高低直接影响运动员和教练员的训练目标和备战目标的制定和实施，同时影响运动成绩的发展特征和规律的发现[1-3]。目前，体育竞赛成绩的预测方法主要有统计法和神经网络法，前者需要搜集大量历史数据，后者的预测结果易受其参数选择的影响。

针对神经网络算法学习速度慢和局部最优的缺点，Huang[4]提出一种新的单隐含层前馈神经网络-极限学习机(Extreme Learning Machine，ELM)，该方法对处理非线性数据具有很强的适应性，但其参数随机产生会影响预测效果。

针对极限学习机预测结果易受其初始化输入权值和偏置值的影响，将果蝇优化算法[5](Fruit Fly Optimization Algorithm，FOA)引入ELM进行权值和偏置优化，并将其应用于体育竞赛成绩预测。选择第23～29届奥运会男子100、200、400、800、1 500、5 000、10 000 m 7 个项目的已有成绩作为研究对象，运用FOA_ELM实现第30届奥运会相应项目的成绩预测，验证FOA_ELM进行体育竞赛成绩预测的可行性和可靠性。

1 果蝇优化算法

FOA算法步骤如下[5]：

Step1：设置FOA算法参数：果蝇种群规模popsize、迭代次数Iteration，果蝇群体初始位置分别为X_begin和Y_begin；

Step2：更新果蝇个体寻优方向和距离，如式(1)、(2)。

xi=X_begin+Value×rand()

(1)

yi=Y_begin+Value×rand()

(2)

其中，xi、yi表示果蝇个体的位置，Value表示搜索距离；

Step3：计算果蝇个体和原点之间的距离di，在此基础上计算果蝇个体的味道浓度si，如式(3)、(4)。

(3)

(4)

Step4：计算适应度函数值，获得果蝇个体在当前位置的味道浓度，如式(5)。

Smelli=Function(si)

(5)

Step5：迭代寻优，找到最佳适应度和最佳位置，分别为Smellb和(xb,yb)；

Step6：记录并保留寻优结果，令Smellbest=Smellb， X_begin=xb，Y_begin=yb，寻着果蝇群体最佳位置方向搜索；

Step7：重复执行Step2-Step5，若当前味道浓度大于前一位置的味道浓度，则执行Step6；反之，则执行Step2-Step5。

2 极限学习机

极限学习机[4]是一种新型的单隐含层前馈神经网络(single-hidden layer feed-forward neural networks，SLFNs)，其是在Moore-Penrose矩阵理论基础上所提出的快速学习算法，其结果示意图，如图1所示。

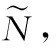
(6)

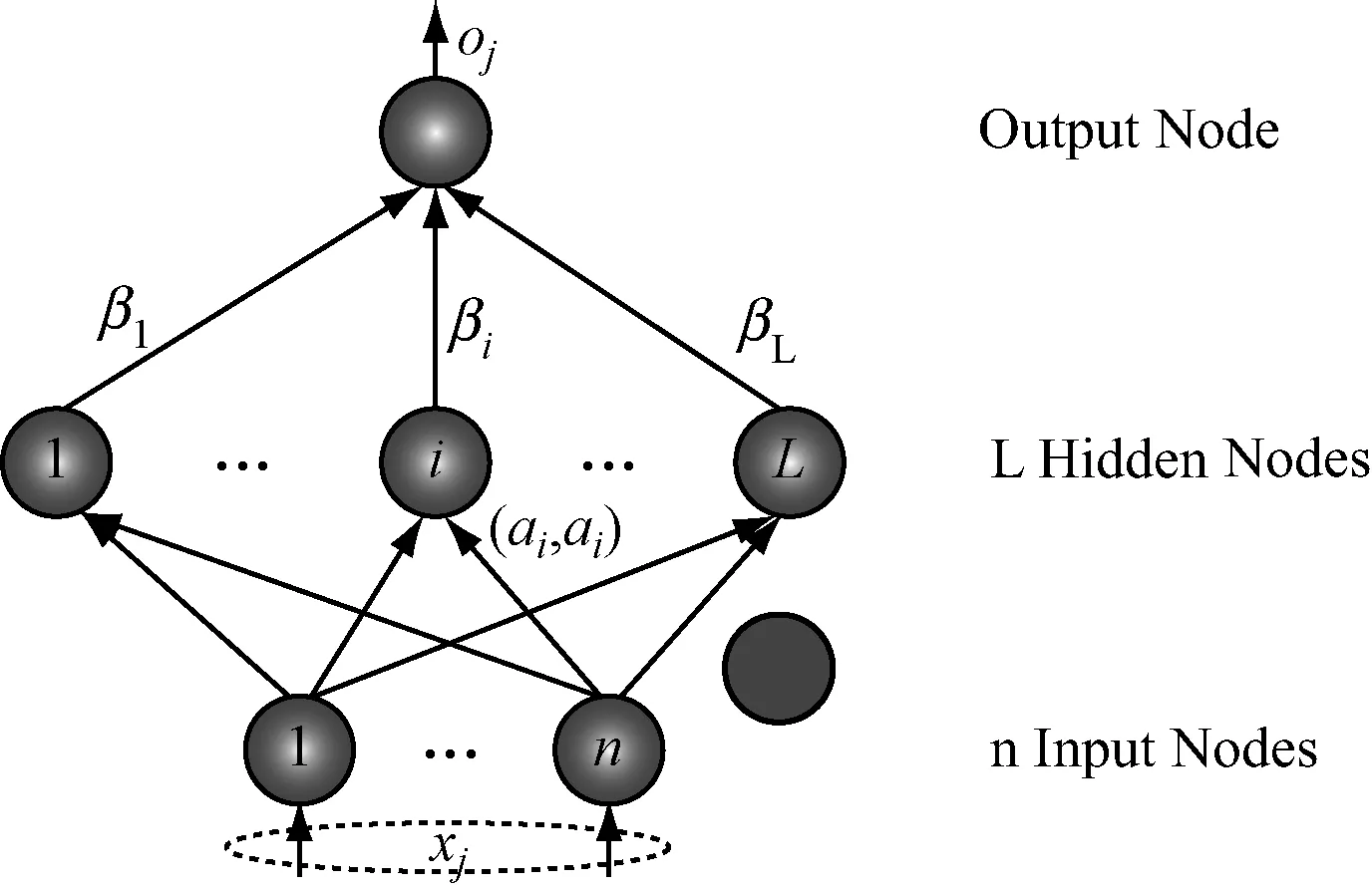
图1 ELM结构示意图

其中，ai=[ai1,ai2,…,ain]T表示第i个隐含层神经元的输入权值；βi=[βi1,βi2,…,βim]T表示第i个隐含层神经元的输出权值；ai·xj表示ai和xj的内积；bi表示第i个隐含层神经元的偏置，可由矩阵，表示为式(7)。

Ηβ=T

(7)

其中式(8)。

(8)

求解该问题就是寻找最优的权值W=(a,b,β)，使代价函数E(W)最小，其数学模型可表示为[7-9]式(9)、(10)。

(9)

(10)

3 基于FOA优化极限学习机的预测模型

针对极限学习机随机输入权重和偏置对预测结果影响较大，如图2所示。

图2 FOA优化ELM流程图

利用FOA算法快速搜索能力和全局寻优能力对ELM的输入权重和偏置进行优化，其适应度函数，为式(11)。

(11)

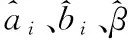
(1) 初始化果蝇算法参数和ELM网络结构参数：果蝇算法最大迭代次数maxgen，种群规模，输入神经元个数inputnum、隐含层神经元个数hiddennum和输出层神经元个数outputnum；

(2) 初始化输入权值、输出权值和偏置；

(3) 原始数据分成训练样本和测试样本，将训练样本输入ELM，根据适应度函数式(11)计算果蝇个体的适应度函数值，寻找果蝇个体和全局最优果蝇个体的位置和最优值；

(4) 更新果蝇的位置和搜索方向；

(5) 计算评估适应度大小并更新更新果蝇的位置和搜索方向；

4 实证分析

4.1 数据来源

为实现第31届奥运会男子田径项目成绩的预测，本文选取第24～30届奥运会男子100、200、400、800、1 500、5 000、10 000 m 7 个项目的冠军成绩为研究对象[6-7]，数据如表1所示。

4.2 评价指标

为了评价体育竞赛成绩预测的效果，选择平均绝对百分比误差(mean absolute percentage error，MAPE) 、平均绝对误差(mean absolute error，MAE) 和均方根误差( root mean square error，RMSE) 作为预测结果的评价指标，评价如式(12)～(14)。

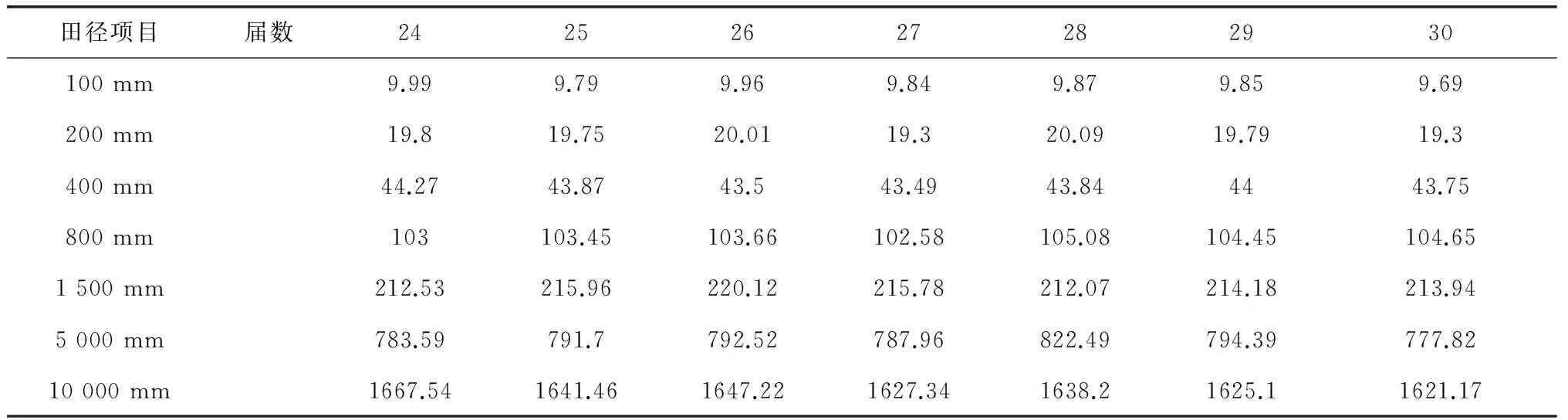
表1 奥运会男子田径项目冠军成绩(成绩单位：秒)

(12)

(13)

(14)

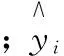
4.3 实验结果

预测方法采用滚动预测方式[8-9]，即用第24～28届成绩来预测29届成绩，用第25～29届成绩来预测30届成绩，用第26～30届成绩来预测31届成绩，反复训练直到满足精度要求，此时成绩即为预测成绩。果蝇算法参数设置如下：最大迭代次数maxgen=100，种群规模popsize=10，极限学习机参数设置如下：输入神经元个数inputnum=7、隐含层神经元个数hiddennum=30和输出层神经元个数outputnum=7，FOA-ELM的体育竞赛成绩预测结果，如图3所示。如图3～图5和表2所示。

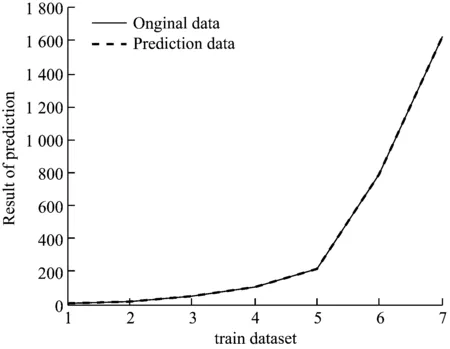
(a) 训练样本预测结果

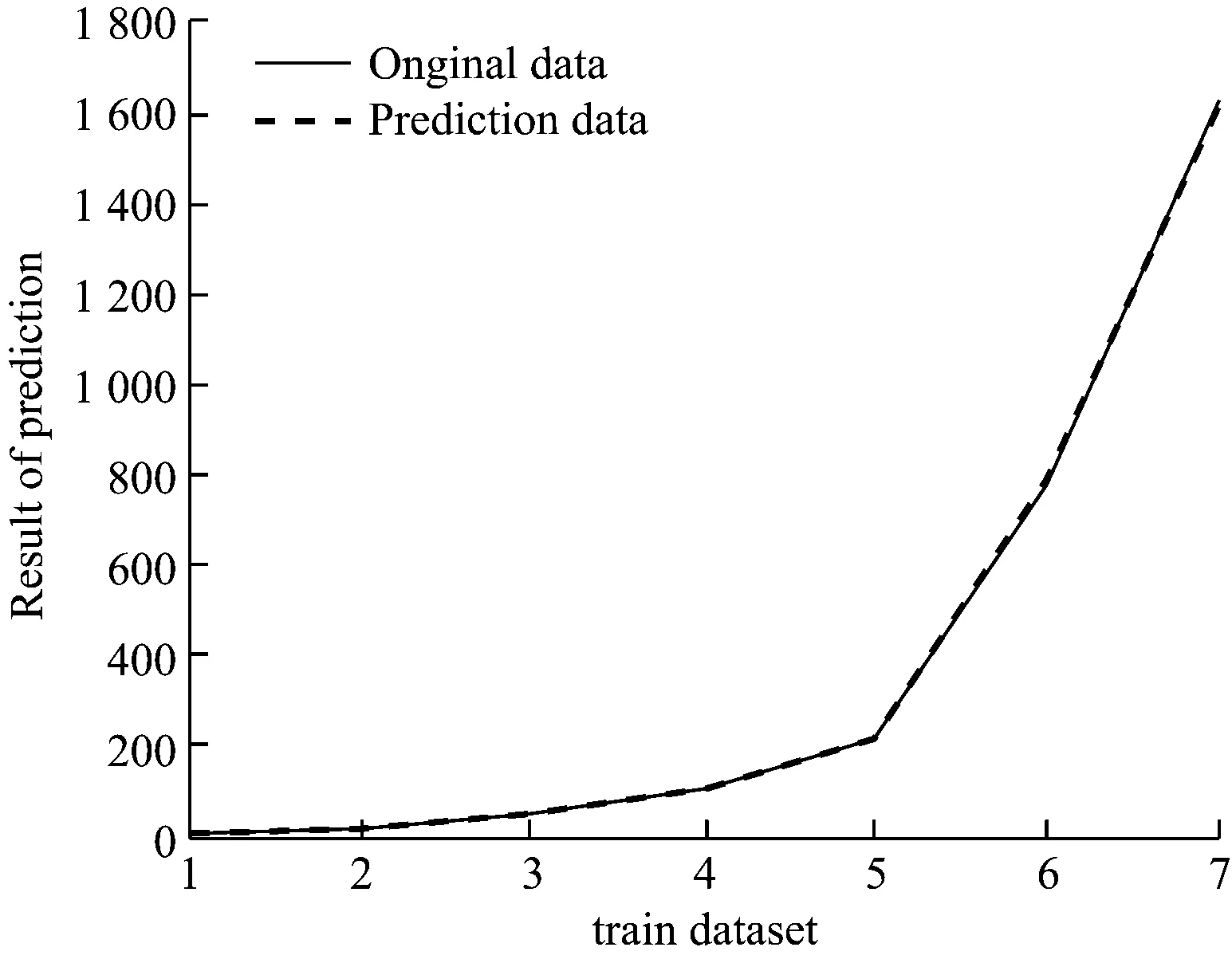
(b) 测试样本预测结果

图3 FOA_ELM预测结果

(a) 训练样本预测结果

图4 ELM预测结果

结合图3-图5和表2不同算法进行短期风速预测结果可知，在RMSE、MAE和MAPE三个评价指标上，FOA-ELM的预测精度最高，优于PSO-ELM[10]、GA-ELM[11]、SOA-ELM[13]、DE-ELM[12]和ELM[14]；其次，GA-ELM的预测精度优于PSO-ELM、SOA-ELM、DE-ELM和ELM；最后，ELM的预测精度最差，RMSE、MAE和MAPE分别比FOA-

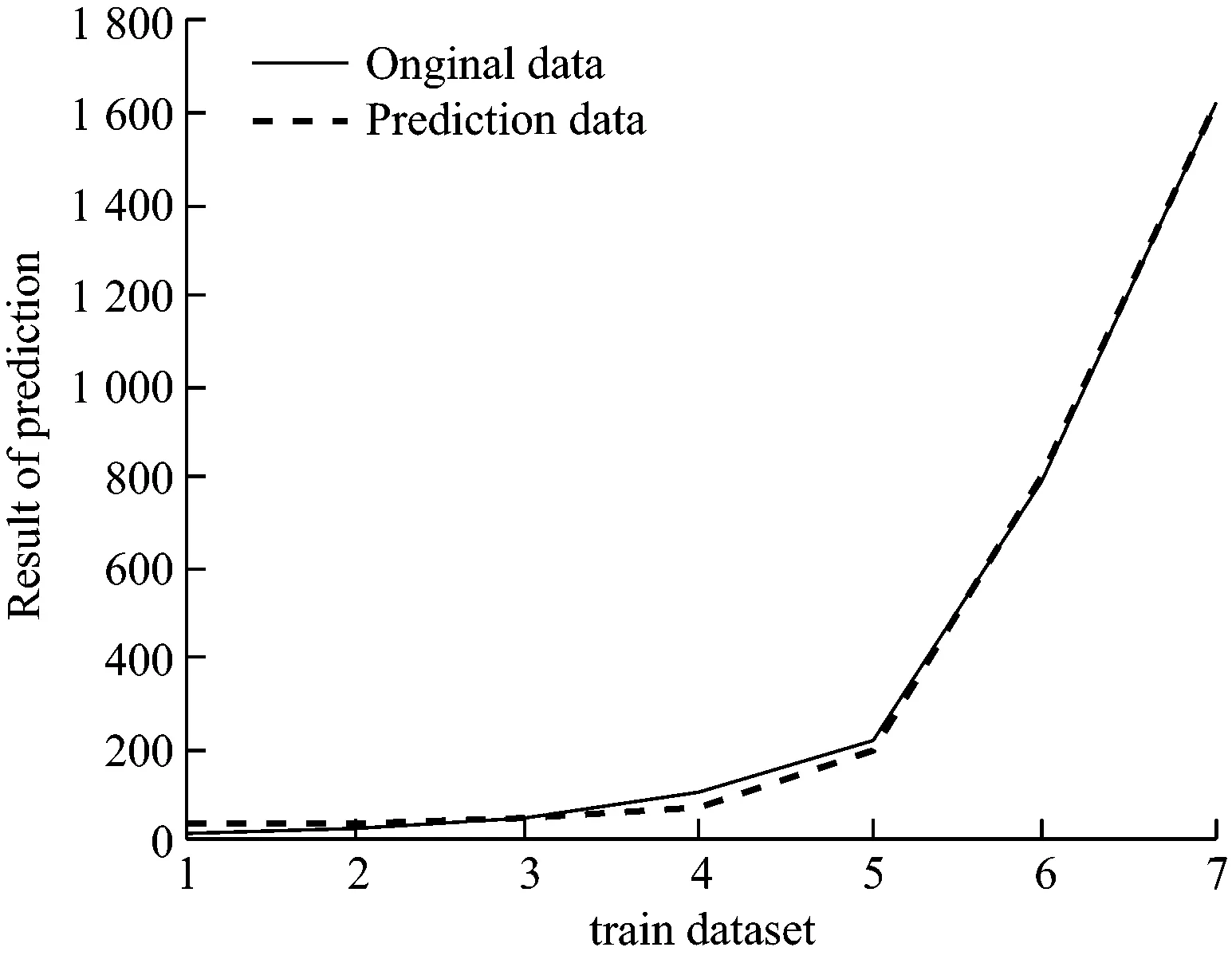
(a) 训练样本预测结果

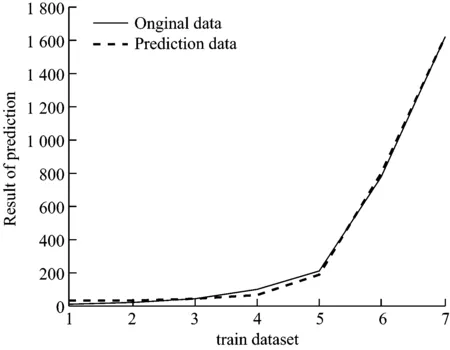
(b) 测试样本预测结果

图5 RBF预测结果

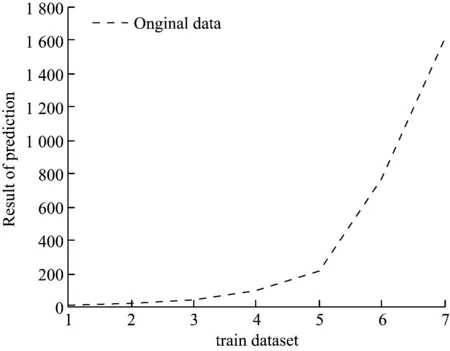
图6 FOA-ELM预测结果

方法RMSEMAEMAPE时间/sFOA-ELM0.31940.18442.2032%4.67PSO-ELM0.38340.24202.8478%10.35GA-ELM0.35990.20572.4322%13.61SOA-ELM0.45940.31073.6194%24.20DE-ELM0.37370.24072.8192%61.67ELM0.82260.62657.3074%3.42

ELM低0.5032、0.4421和5.1042%，通过对比可知，运用群智能算法对ELM的输入权值、输出权值和偏置进行优化，可以有效提高ELM的预测精度，其中FOA算法对ELM的优化效果最好，同时耗费的时间除ELM之外也远低于其他智能算法。

5 总结

针对极限学习机预测结果对其输入权值和偏置值的选择敏感的特点，提出一种基于果蝇算法优化极限学习机的体育成绩预测模型。研究结果表明，与其他智能算法优化ELM的结果对比可知，FOA-ELM在预测精度和计算效率上，均优于其他智能算法，从而验证本文方法的有效性和可靠性。

[1] 郭维民. GM(1,1)与BP神经网络组合预测模型在田径成绩预测中的应用[J]. 体育研究与教育, 2013(5):95-97.

[2] 范文杰, 刘芳. GM(1,1)模型在田径成绩预测中的运用[J]. 重庆工商大学学报(自然科学版), 2001, 18(3):63-66.

[3] 魏春玲, 孙晋海. 奥运会田径项目成绩发展趋势及灰色预测研究[J]. 中国体育科技, 2005, 41(2):18-20.

[4] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1-3):489-501.

[5] Wen-Tsao Pan.A new fruit fly optimization algorithm: Taking the financial distress model as an example[J]Knowledge-Based Systems.2012(26) :69-74.

[6] 杜娜娜, 杜少武, 林慧. 我国城市运动会田径速度类项目成绩发展趋势及灰色预测研究[J]. 中国体育科技, 2012, 48(6):10-13.

[7] 王伟. 系统论及马尔柯夫模块理论在田径运动成绩预测中的应用研究[J]. 南京体育学院学报社会科学版, 2004, 18(6):85-87.

[8] 宋小凤. 田径短跑成绩变化趋势动态预测仿真研究[J]. 计算机仿真, 2016(10):417-420.

[9] 张宇, 袁晓曦, 弓小倩. 基于BP神经网络算法的体育成绩预测研究[J]. 科技通报, 2013(6):149-151.

[10] 王杰, 毕浩洋. 一种基于粒子群优化的极限学习机[J]. 郑州大学学报(理学版), 2013, 45(1):100-104.

[11] 高彩云, 崔希民, 高宁. 熵权遗传算法及极限学习机地铁隧道沉降预测[J]. 测绘科学, 2016, 41(2):71-75.

[12] 王芳, 续欣莹, 阎高伟. 基于自适应差分进化算法优化极限学习机的球磨机料位测量[J]. 仪表技术与传感器, 2015(6):143-145.

[13] 余胜威, 曹中清. 基于人群搜索算法的PID控制器参数优化[J]. 计算机仿真, 2014, 31(9):347-350.

[14] Huang G B, Zhou H, Ding X, et al. Extreme learning machine for regression and multiclass classification.[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society, 2012, 42(2):513.