基于保边IBP和结构相似性的超分辨率图像重建算法

卜宇， 梁传君

(新疆工程学院，计算机工程系，乌鲁木齐 830052)

0 引言

最近的几十年中，超分辨率[1](Super Resolution，SR)理论和技术发展非常迅速，应用极其广泛，如地形分类、矿物检测和勘探、遥感制图、环境监测、以及军事监视等[2][3]。由于仪器限制和不完美成像光学器件，外界的影响，如大气湍流，成像中的噪声等造成传感器相元分辨率变低，提高硬件上的成像技术代价比较高，不适用于民用和军事领域所需要性能和价格，因此，如何提高成像的分辨率是一个重要的研究课题。

在实践中，修改成像光学器件或传感器阵列代价太大，而且传感器阵列的密度已经趋于饱和[4]，提升的可能性不大，从软件算法角度提高分辨率是一种切实可行的方案[5][6]。超分辨率重建的主要思想是将多个低分辨率(Low Resolution, LR)图像重建为一个或多个高分辨率(High Resolution, HR)图像。

已经有很多学者对超分辨率问题进行了研究。一般SR算法一般分为三大类：基于插值的算法，基于学习的算法和基于重建的算法。

基于插值算法的主要优点是算法简单，运行速度快，如文献[7]提出了一种改进的插值算法，添加了更多的先验知识，如平滑先验和噪声先验，但边缘，角点，使用简单的平滑先验来重建HR图像将会产生振铃、模糊、鬼影等效果。

基于重建的SR算法主要利用正则化对各种平滑先验知识约束求解。如文献[8]提出了一种利用自身实例图像的SR问题，其中就用到了高斯先验和L2正则化进行鲁棒估计，不过病态问题，即许多HR图像能产生相同的LR图像，并没有明显得到缓解，对异常点(outlier)处理也比较乏力。

基于学习的SR算法中，细节纹理通过LR/HR训练图像集搜索获得。这些纹理细节需要训练图像的精细选择，否则将匹配错误的纹理细节。文献[9]提出了基于多尺度结构自相似性的单幅图像超分辨率算法，充分利用结构自相似性在多尺度上的应用，效果也不错，但实例比较理想化，从LR图像块到HR图像块的映射病态问题没有很好的解决。

考虑到任何观察到的场景中经常有许多重复的物体和自然图像的结构相似性属性，本文引入一个新的超分辨率重建算法，将结构相似性结合改进的具有保边效果的迭代反投影(iterative back projection, IBP)，提出的算法既有IBP算法的快速特性，又有较高的重建效果。

1 具有保边效果的IBP

1.1 迭代反投影算法IBP

迭代反投影的SR重建方法[10]类似于在断层摄影中使用的背投影。在这种方法中，HR图像估计由模拟LR图像之间的差值估计得到，终止迭代的条件是成像模糊图像和观察LR图像的误差最小，其简要示意图，如图1所示。

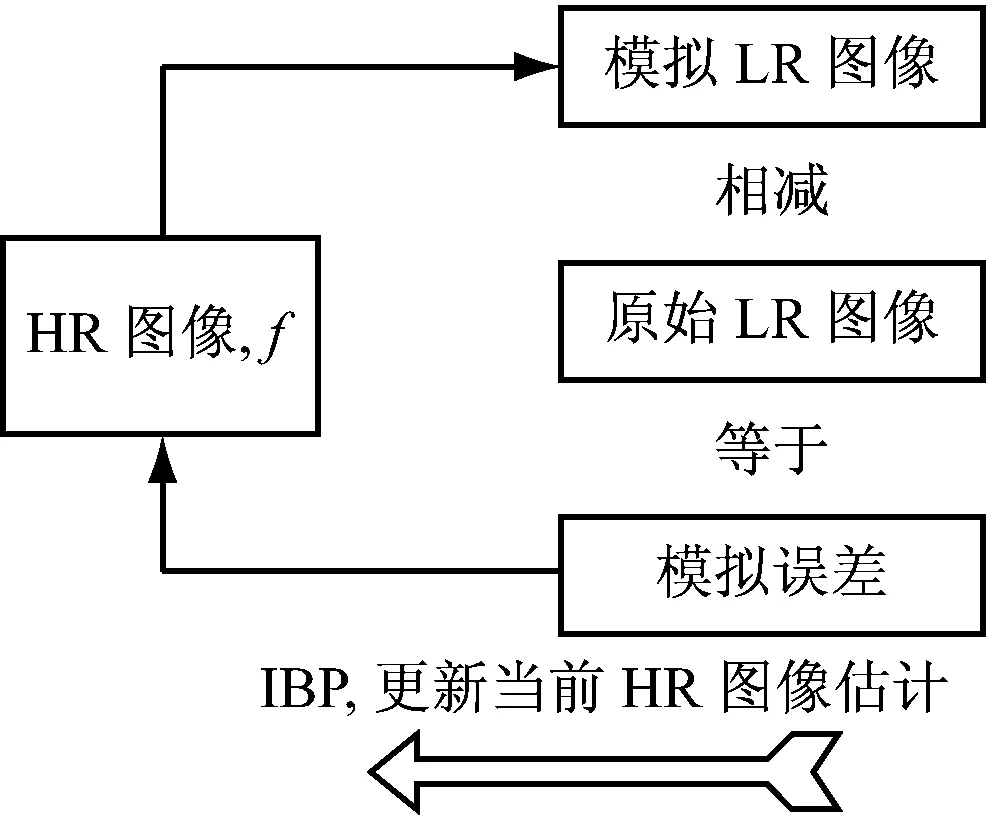
图1 IBP算法流程的示意图

IBP估计HR图像表示如式(1)。

gk(m,n)=σk(h(f(x,y))+ηk(x,y))

(1)

式(1)中，gk表示第k个观察图像帧；f表示潜在的高质量图像；h表示模糊算子；ηk是加性噪声项，一般用高斯白噪声表示；σk是一个图像像素抽样离散化的非线性函数。σk还包括第k帧的位移;(x,y)高质量图像f的中心。

一般先初始化一个高分辨率图像HR，即先将LR图像通过插值的方式将其分辨率上采样为所要的分辨率，模拟图像降质的过程，以获得一组对应于所观察到的输入图像的模拟LR图像。模拟LR图像应该与原始LR图像相减，即获得差分图像，这种模拟误差随着HR的更新而变化，重复该迭代过程最小化误差函数,如式(2)。

(2)

式(2)中，gk的第n次迭代模拟成像过程,如式(3)。

(3)

式(3)中，↓s表示下采样因子为s的下采样操作，Tk是σk的逆运算，HR图像的迭代更新为式(4)。

(4)

式中，K是低分辨率帧的数量，↑s是上采样因子为s的上采样操作，*是卷积运算符，hBP是一种“反投影”内核，取决于模糊算子h和Tk确定。

1.2 具有保边效果的IBP

各向异性扩散的目的是结合边缘增强，保持图像亮度的边界，因此各向异性扩散可以从几个重叠模糊LR图像重建一个HR图像，而且保留和增强边缘，同时减少在恢复过程中图象噪声[11]。其扩散过程,表示如式(5)。

(5)

式中，X表示浓度，D表示扩散张量，即一个正定对称矩阵，式(2)可以被改写为式(6)。

(6)

式(6)中，gk(x)是SR图像X.在这种情况下的变换后的图像时，相应的梯度下降方程,表示为式(7)。

(7)

与传统的低通滤波和线性扩散相比，掺入的边缘增强各向异性扩散到SR中的特性具有明显的提升效果，其中标量由2×2弥散张量D上进行如下替换，即式(7)可以改写为式(8)、式(9)。

(8)

(9)

2 结合结构相似性的保边IBP

为了得到更多先验知识，完全可以考虑结构相似性，自然图像都拥有大量的自相似小图像块，这是局部图像结构在不同尺度下的重现[9][12]，即在某个自然图像上取一个4×4的小图像块，一定能在这幅图像上找到和这一图像块最匹配的图像块。这是自然图像非常重要的属性，将其先验性运用到图像重建中将非常有益[14]。

本文在保边IBP的基础上，引入图像块相似性作为图像重建的新的先验知识。于是修改式(6)得到式(10)。

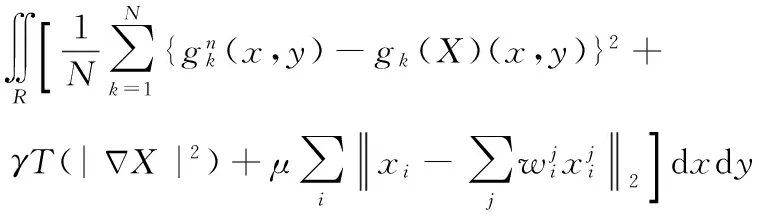
(10)

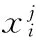
(11)

式中，h是归一化因子，t是控制相似度的标量。式(10)可以简化为式(12)。

(12)

式中，I是单位矩阵，A是N×N的矩阵，N是原始超分辨率图像维数。矩阵A中[14]元素满足式(13)。

(13)

对初始的高分辨率图像分块处理，可求出矩阵A。整个算法流程图,如图2所示。

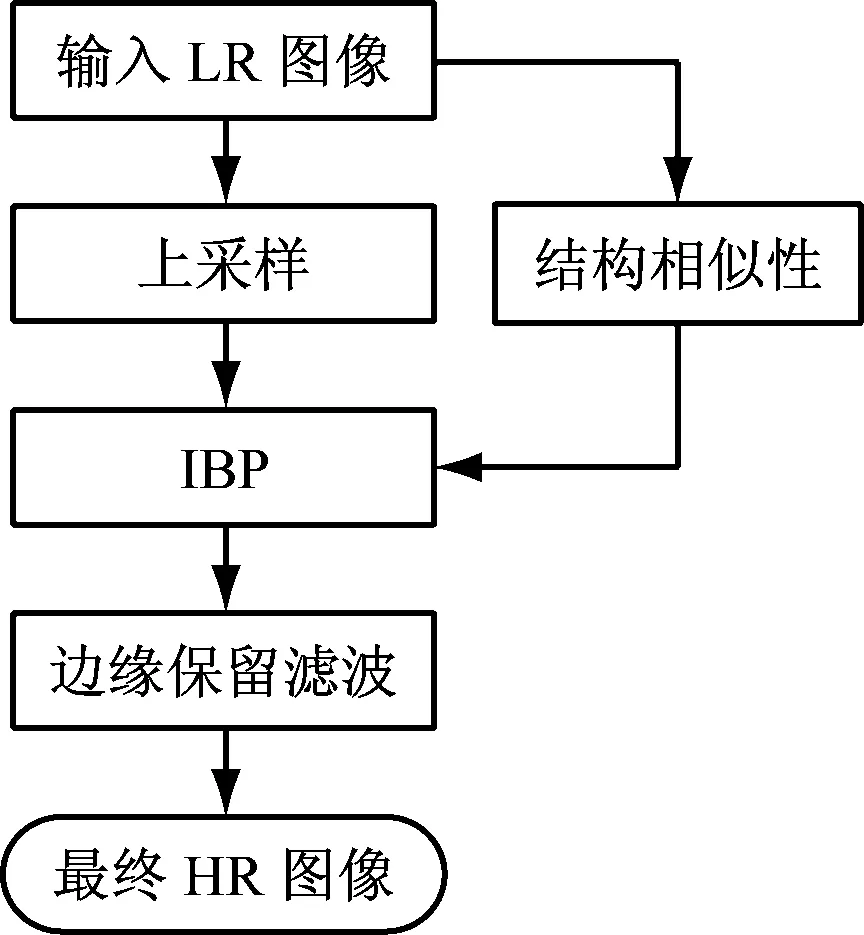
图2 算法流程图

3 实验与分析

仿真实验在配置为Win7操作系统、intel酷睿II处理器、1.86 GHz主频、2.95 GB RAM的笔记本计算机进行。使用MATLAB 7.1平台。

3.1 算法参数设置及评价函数

本文选择的小图像块尺寸为a=6，判断块与块之间关系阈值T取3，控制相似度的标量t取0.02。IBP迭代最高次数为8次，IBP的内核的σ值选择在0.8到1.5之间。经过6次迭代就已经收敛了,如图3所示。

图3 IBP的迭代次数与误差关系图

本文使用图像的峰值信噪比(Peak Signal to Noise Ratio, PSNR)和结构相似性指标(Structural Similarity Index Measurement, SSIM)表征估计得到HR图像的好坏，其中PSNR可以表征图像高频成分损失情况，越高越好，SSIM是一种衡量两幅图像的相似程度，最大值为1，越接近1表示越相似，SSIM非常符合人眼对图像品质的判断。

图像亮度分量均值表达形式为式(14)。

(14)

其中bins(i)代表亮度为i的直方图条块的高度，PSNR的形式为式(15)。

(15)

SSIM定义为式(16)。

(16)

式中，ux及uy、σx及σy分别为图像x，y的平均值和标准差，σxy为x，y的共变异数，C1,C2,C3都为常数。一般情况下，取图像局部性视窗，遍历整个图像，直到整个图像的SSIM计算完毕，将全部的SSIM平均起来为x，y图像的结构相似性指标。

3.2 定量分析

实验所用图像大多采自文献[8][14][15]，图2为用于比较测量的图像，比较的算法是文献[8]提出Huber函数双变分重建算法(HBTV)，文献[15]提出的一种实例回归的算法(IPER)和单纯的IBP。

为了获得客观的测量结果，首先使用SSIM表征结果，如表1所示。

表1 分辨率增强因子为2时各算法SSIM结果

从表1可以看出立方插值的结果最差，因为立方插值假设图像总是平滑先验的。IPER，IBP和HBTV的效果明显好于立方插值，SSIM都比立方插值的大。本文算法大多数情况下拥有最高的SSIM值，这是由于该方法组合了更多的先验知识，获得更好的结果。

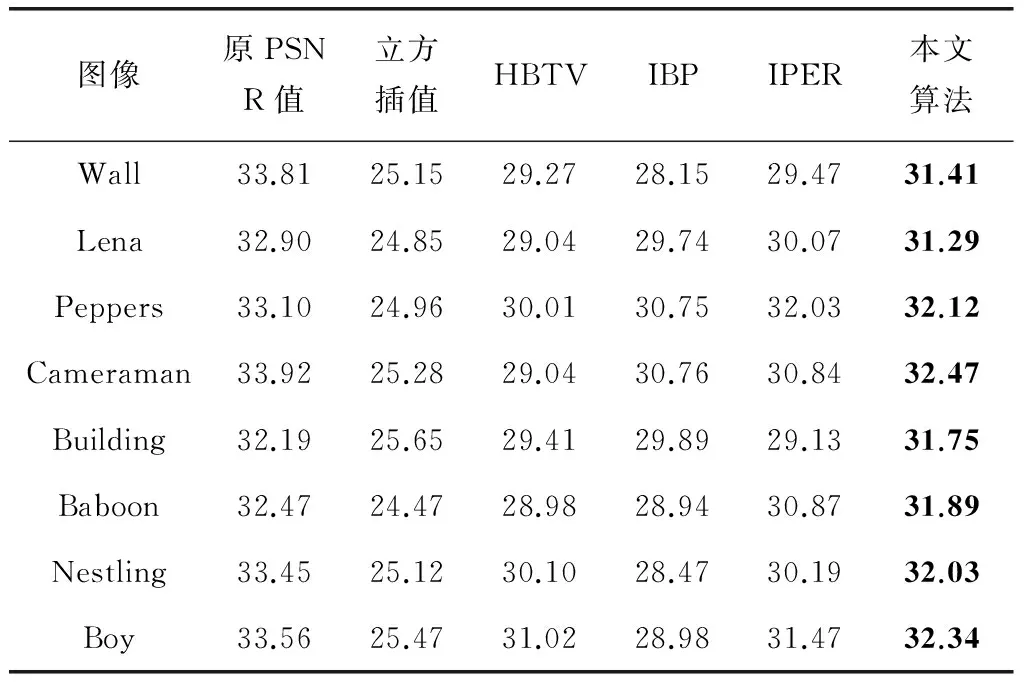
表2是PSNR的值测量结果，PSNR值越高表示图像的高频成分越多，如表2所示。

从表2可以看出本文算法的PSNR值最高，与原始图像的PSNR值相差最少，效果最好。

3.3 定性分析

不同算法在“Wall”，“Nestling”和“Cameraman”的结果，可以看出，从“Wall”图像上，IBP、HBTV和IPER算法都有鬼影和振铃效应，造成了视觉的不舒服，石头的层次和纹理不是非常差明朗，而本文算法石头的层次感强，在“Nestling”图像中，本文算法能显示出更细腻的雏鸟的毛发。另外其他三种算法在“Cameraman”图像上的细节都有些模糊。从对比可以看出，本文算法重建的结果最自然准确,图4，图5和图6分别所示了。

图像原PSNR值立方插值HBTVIBPIPER本文算法Wall33.8125.1529.2728.1529.4731.41Lena32.9024.8529.0429.7430.0731.29Peppers33.1024.9630.0130.7532.0332.12Cameraman33.9225.2829.0430.7630.8432.47Building32.1925.6529.4129.8929.1331.75Baboon32.4724.4728.9828.9430.8731.89Nestling33.4525.1230.1028.4730.1932.03Boy33.5625.4731.0228.9831.4732.34

3.4 处理速度比较

一个好的SR算法应该满足以下三大方面：图像纹理，图像自然性和算法处理的速度。本文算法具有IBP的快速特性，添加的先验知识可以被快速计算,如表3所示。

表3 各算法的平均运行时间比较(s)

从表3可以看出，插值算法依然最快，因为插值算法最简单。对于256×256的图像“Wall”，“Nestling”和“Cameraman”，在matlab7.1平台上，比较平均运行时间，可以看出本文算法运行时间比IPER和HBTV的短，与纯IBP差不多。

4 总结

超分辨率图像重建可以克服成像系统固有分辨率的限制，改善成像性能。本文提出一种混合算法，即改进的IBP结合结构相似性的先验知识，该算法可以提高图像对比度，同时恢复退化的细节，相比于其他优秀算法，拥有更多的先验，从实验结果看，重建的图像更准确自然，运行速度更快。

未来将重点研究使用数据库较少的学习方法，结合适当正则化，建立联合字典的SR方法，讨论如何快速准确地LR图像对HR图像块的映射病态问题。

[1] 杨宇翔. 图像超分辨率重建算法研究[D]. 合肥:中国科学技术大学, 2013.

[2] 苏衡, 周杰, 张志浩. 超分辨率图像重建方法综述[J]. 自动化学报, 2013, 39(8):1202-1213.

[3] 杨文波. 航空图像超分辨率重构技术研究[D]. 长春:中国科学院研究生院(长春光学精密机械与物理研究所), 2014.

[4] 江毅, 黄俊斌. 基于波分复用器的光纤光栅振动传感器阵列[J]. 中国激光, 2005, 32(11):1525-1528.

[5] Zhang H, Zhang L, Shen H. A super-resolution reconstruction algorithm for hyperspectral images[J]. Signal Processing, 2012, 92(9): 2082-2096.

[6] Zhang L, Zhang H, Shen H, et al. A super-resolution reconstruction algorithm for surveillance images[J]. Signal Processing, 2010, 90(3): 848-859.

[7] Mallat S, Yu G. Super-Resolution With Sparse Mixing Estimators[J]. IEEE Transactions on Image Processing, 2010, 19(7):2889-2900.

[8] 梁风梅, 邢剑卿, 罗中良,等. 基于Huber函数双边全变分的多帧文档图像超分辨率重建[J]. 中山大学学报(自然科学版), 2014, 21(4):74-78.

[9] 潘宗序, 禹晶, 胡少兴,等. 基于多尺度结构自相似性的单幅图像超分辨率算法[J]. 自动化学报, 2014, 40(4):594-603.

[10] 首照宇, 廖敏璐, 张彤. 基于IBP改进和稀疏表示的图像超分辨率重建[J]. 计算机工程与设计, 2014, 35(3):934-938.

[11] Ma J, Plonka G. Combined Curvelet Shrinkage and Nonlinear Anisotropic Diffusion[J]. IEEE Trans Image Process, 2007, 16(9):2198-2206.

[12] 吴炜, 郑成林, 张莹莹,等. 广义非局部均值和自相似性的超分辨率算法[J]. 西安电子科技大学学报, 2014, 27(4):100-107.

[13] 王素玉, 卓力, 沈兰荪,等. 一种用于动态视频超分辨率的多尺度最小二乘仿射块匹配图像配准方法[J]. 电子与信息学报, 2009, 31(3):542-545.

[14] Dong W SH, SHI G M, and Zhang L, Super-resolution with nonlocal regularized sparse representation [C]//Proc. SPIE Visual Communications and Image Processing, 2010: 1-10.

[15] Yang J, Lin Z, Cohen S. Fast Image Super-Resolution Based on In-Place Example Regression[J]. IEEE Conference on Computer Vision & Pattern Recognition, 2013, 9(4): 1059-1066.