不确定箱重下内河集装箱班轮航线配载决策

李 俊，张 煜*，计三有，程 昭，马 杰

(武汉理工大学a.物流工程学院；b.航运学院，武汉430063)

0 引言

集装箱运输需求的增加对班轮航线配载决策提出了更高要求.内河集装箱班轮由于体型较小，船舶稳性对配载计划十分敏感，少量集装箱堆放位置变化或重量偏差可能导致配载计划失效.对于内贸箱而言，货主提供箱重信息的不确定性导致内河集装箱班轮航线配载决策变得更加复杂.

已有的航线配载决策研究大多围绕集装箱海运展开，往往假设航线上各港口节点的集装箱信息已知，采用的方法包括启发式算法[1-3]、遗传算法[4]、整数规划[5]、帕累托聚类搜索[6]等.这些研究未考虑不确定因素对航线配载决策影响，且主要针对海运展开.内河集装箱班轮运输与海运相比往往更强调舱容利用率，船舶稳性对配载计划脆性较强.同时航线配载决策会受到集港过程中不确定箱重影响，已有研究配载效率退化明显，无法适应内河集装箱班轮航线配载决策需求.

内河集装箱班轮航线运输中，内贸箱箱重信息具有不确定性，采用随机变量描述，约束条件中包含随机变量的航线配载决策问题属于随机规划问题.目前，与集装箱运输相关的随机规划研究主要关注班轮航线规划[7]、集装箱舱位分配[8]、堆场容量需求[9]等.已有研究表明随机规划可有效应对不确定因素干扰，提高方案抗干扰能力.

本文考虑内河集装箱班轮运输中内贸箱不确定箱重影响，对班轮航线配载决策进行研究，构建随机规划和随机机会约束规划模型，并设计混合邻域搜索算法求解.最后通过算例研究和蒙特卡罗随机模拟验证算法的有效性.

1 问题描述

内河集装箱班轮航线配载决策中，当前港口输出的配载计划将作为制定下一港口配载计划的输入，如图1所示.班轮在航行过程中顺序遍历多个港口节点，在到达各港口节点之前，船方利用货主提供的订舱信息完成当前节点的预配计划和后续节点箱位预留.当前节点结合集装箱实际集港信息，基于船方制定的预配计划完成船舶实配计划.针对内贸箱而言，实际中为了降低运输成本，货主在向船方订舱时存在瞒报集装箱重量信息的情况，导致实际箱信息发生变化.而船方利用货主提供的箱信息进行配载，使配载计划隐含极强脆性.

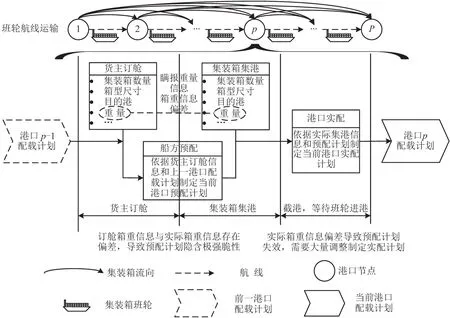
图1 内河集装箱班轮航线配载决策Fig.1 Inland container liner route stowage planning decision

因此，对于内贸箱而言，需要考虑集港过程中不确定箱重对航线配载决策的影响，在满足船舶稳性、强度及容量等约束前提下，综合考虑航线各港口节点之间的运输需求，制定航线各挂靠港的配载计划.考虑到内河集装箱班轮运输的独特性，航线配载决策的目标为最小化航线班轮堆栈占用数量，实现被占用堆栈的高效利用，保证船舶的舱容利用率.

2 模型构建

2.1 假设条件

针对内河集装箱班轮航线运输的特点，考虑现实约束，做出以下假设：

(1)考虑同一尺寸的普通箱；

(2)货主在向船方订舱时存在瞒报集装箱重量信息的情况；

(3)参考国家交通运输部发布的《载货集装箱累加计算法重量验证指南》，集装箱箱重在货主提供重量的基础上最大偏差设为1 t.

2.2 模型建立

为了方便建模，将班轮贝位内堆栈按前半部、后半部、左半部、右半部分成不同的堆栈集合，如图2所示.

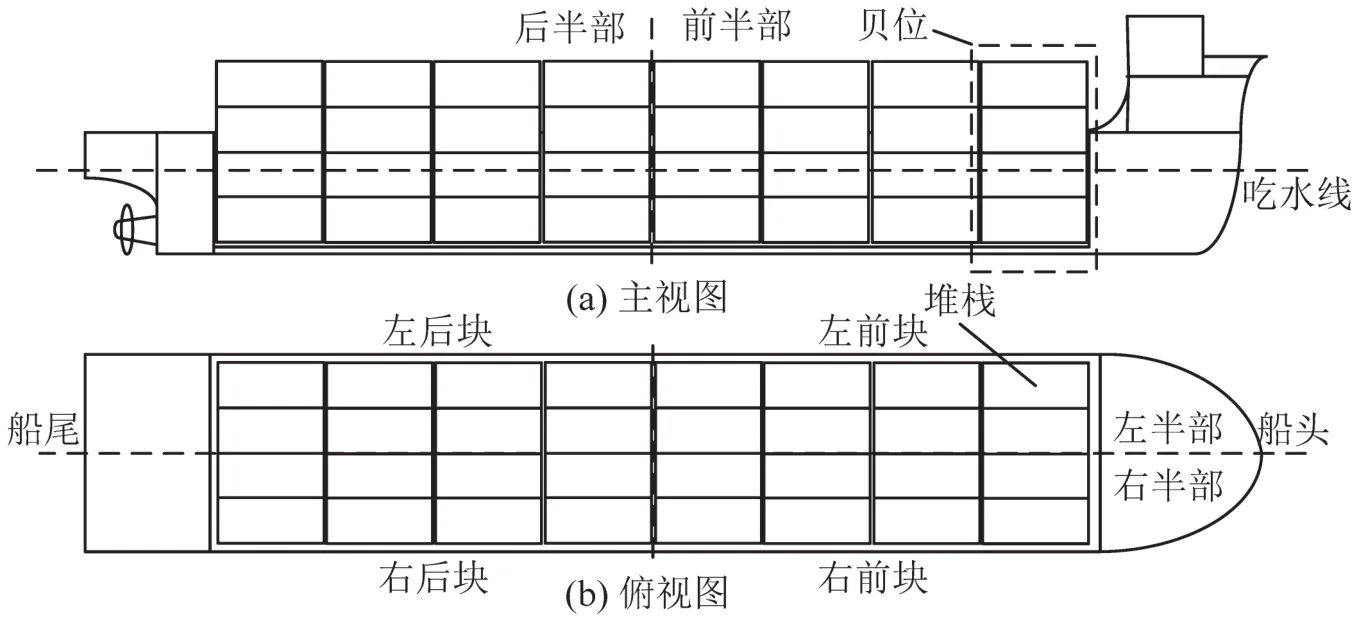
图2 内河集装箱班轮结构Fig.2 Structure of inland container liner

模型参数设置如下：

(1)集 合.

P——航线港口集合；

Q(p)——航线上港口p的OD副集合，Q(p)=Qt(p)⋃Qs(p),∀p∈P；

Qt(p)——航线上途径港口p的OD副集合，Qt(p)={a|o,p,d∈P,o＜p＜d,a=(o,d)}；

Qs(p)——航线上从港口p始发的OD副集合，Qs(p)={a|o,p,d∈P,o=p＜d,a=(o,d)}；

G——集装箱重量等级集合(轻、中、重)，G={1,2,3}；

J——班轮堆栈集合，J=JF⋃JA=JL⋃JR；

JF、JA——班轮前、后半部堆栈集合；

JL、JR——班轮左、右半部堆栈集合.

(2)参 数.

Ng(a)——港口p流向后续港口d的重量等级为g的待装船集装箱箱量(TEU)，∀a=(o,d)∈Qs(p),p∈P,g∈G；

wg——重量等级为g的集装箱平均重量(t)，g∈G；

——重量等级为g的集装箱随机重量(t)，g∈G；

ΔCG、ΔLG——班轮允许的最大横、纵向重量差(t)；

STj——班轮堆栈j的最大箱位容量(TEU)，∀j∈J；

SWj——班轮堆栈j的最大载重量(t)，∀j∈J；

L——一个大数.

(3)变 量.

xjg(a)——班轮堆栈j内OD副a流向下重量等级为g的集装箱箱量(TEU)，∀g∈G,j∈J,a∈Q(p),p∈P；

yj(a)——0-1变量，若班轮堆栈j被OD副a流向下的集装箱占用则为1，否则为0，∀j∈J,a∈Q(p),p∈P.

随机规划模型(Stochastic Programming Model,SPM)为

式(1)为目标函数，表示最小化航线班轮堆栈占用数量；式(2)～式(11)为约束条件.式(2)保证任意港口的集装箱均可装船.式(3)保证任意OD副流向下的集装箱至少占用1个堆栈.式(4)保证任意堆栈至多被1种OD副流向下的集装箱占用，避免出现阻塞箱.式(5)定义决策变量xjg(a)、yj(a)关系，若xjg(a)＞0，则说明堆栈j内堆放有OD副a流向下的集装箱，此时yj(a)=1；反之，若xjg(a)=0，则yj(a)=0.式(6)和式(7)保证任意堆栈均满足容量和载重量约束.式(8)和式(9)保证班轮在任意港口均满足横、纵向重量差约束.式(10)和(11)定义决策变量的取值范围.

将模型SPM中与随机重量相关的约束式(7)～式(9)松弛，得到原问题的下界模型(Lower Bound Model，LBM)为

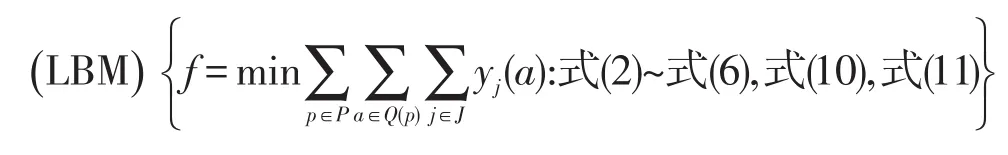
由于式(7)～式(9)均为随机约束，模型SPM无法直接求解.基于随机规划理论，采用机会约束描述随机约束，转化得到随机机会约束规划模型(StochasticChance-constrainedProgrammingModel,SCPM)为

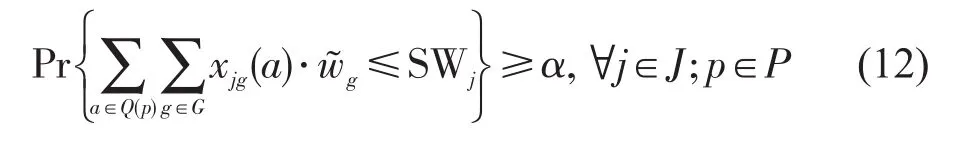
式(12)～式(14),式(10),式(11)}

式中：α为置信水平，α=0.95.

3 混合邻域搜索算法

模型SCPM无法通过已有数学规划软件求解，参考文献[10]中混合智能算法，设计混合邻域搜索算法(Hybrid Neighborhood Search Algorithm，HNS)求解.该算法包含蒙特卡罗随机模拟、神经元网络训练及邻域搜索启发式3个部分.

3.1 蒙特卡罗随机模拟

由式(12)～式(14)得到不确定函数U:x→(U1(x),U2(x),U3(x))，其中：

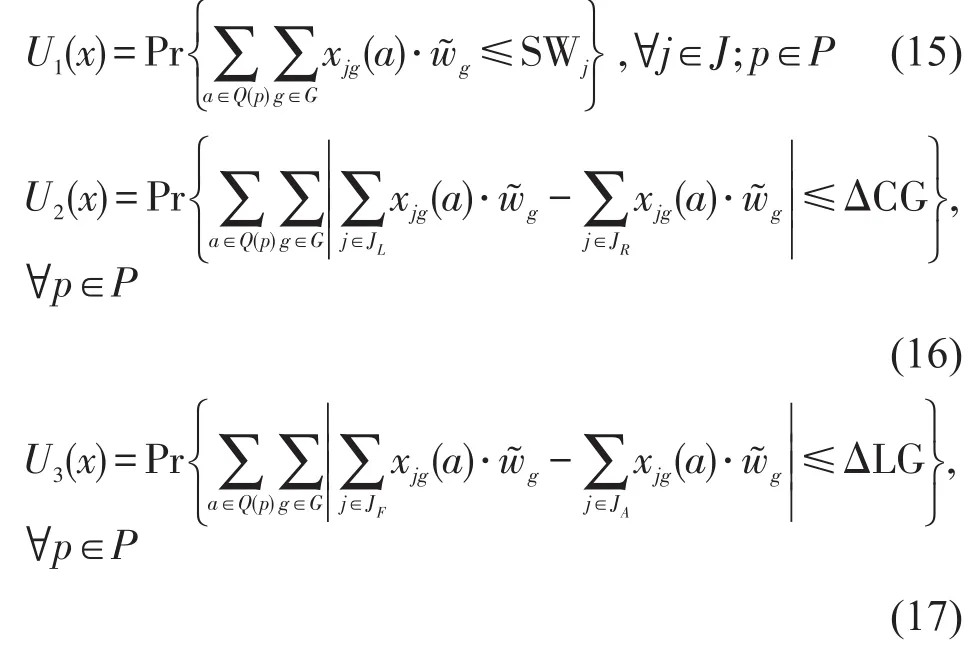
采用蒙特卡罗随机模拟为U:x→(U1(x),U2(x),U3(x))产生输入输出数据，w͂g按g∈G={1,2,3}分别服从[6,8]、[13,15]、[20,22]的均匀分布.

Step 1构建无目标优化模型(CSM1){f=0:式(2)～式(6),式(10),式(11)}，确定待装船集装箱组与班轮堆栈之间的对应关系；

Step 2设置训练样本数量，N0=3 000；

Step 3调用Gurobi求解模型CSM1产生输入数据；

Step 4循环模拟(N1=5 000)得输出数据，记录输入、输出得到1组样本数据；

Step 5重复Step3～Step4至达到样本数量，结束.

3.2 神经元网络训练

利用样本数据训练神经元网络逼近不确定函数U:x→(U1(x),U2(x),U3(x))，包含1个隐含层，采用反向传播法更新权重.每组数据训练5 000次，完毕后保存网络.

3.3 邻域搜索启发式

(1)初始解构造.

Step 1将当前港口待装船集装箱按照OD副、重量等级等属性分组得到集装箱组.

Step 2将集装箱组按照“OD副由近到远、重量等级由轻到重”排序.

Step 3将班轮堆栈按照从“船头到船尾、左侧到右侧”的顺序依次编号.

Step 4考虑堆栈箱位容量约束，将排序后的集装箱组依次堆放至班轮堆栈中，并更新集装箱组和堆栈状态.重复Step4至所有集装箱组装船完毕.由于未考虑载重量和稳性约束，可得到每个OD副a流向下集装箱组最少堆栈占用，记为M(a).

Step 5对于每个OD副流向a，构建无目标优化模型(Container to Stack Model 2,CSM2)，如式(18)和式(19)所示，得到满足堆栈载重量约束的初始配载计划.若模型CSM2无法在有限时间内求解，则更新M(a)=M(a)+1，重复Step5至得到当前港初始配载计划.

(CSM2){f=0:式(2)～式(6),式(18),式(19),式(10),式(11)}

模型CSM2中，式(18)保证最差情形下任意堆栈满足载重量约束；约束(19)保证集装箱组占用尽可能少的堆栈.

(2)初始解优化.

将堆放在任一班轮堆栈内所有集装箱视为1个堆栈箱组，按集装箱重量等级计算各堆栈重量.将班轮堆栈按前后和左右分为左前块、右前块、左后块、右后块，如图2所示.设计3种不同的邻域搜索策略优化初始配载计划，只可对当前港装船的堆栈箱组操作，调整后更新各堆栈重量.

策略1调整堆栈箱组所在位置，快速优化班轮横、纵向重量差.

①纵向重量差调整.ⓐ前半部更重，计算前、后半部重量差值的1/2(记为Δw)，从前半部选取重量最接近Δw的堆栈箱组，将其调整到后半部第1个空堆栈；ⓑ后半部更重，类似地调整.

②横向重量差调整.为了保证已优化的纵向重量差不被改变，调整时只可在前半部或后半部内部的堆栈块之间操作，其他按策略1中①方法类似调整.

策略2互换不同堆栈箱组所在位置，进一步优化班轮横、纵向重量差.

若通过策略1调整后仍无法通过神经网络检验，则继续调整：

①纵向重量差调整.更新Δw，从前、后半部中选取重量差值最接近Δw的2个堆栈箱组互换位置.

②横向重量差调整.同样只可在班轮前半部或后半部内部的堆栈块之间操作，其他按策略2中①方法类似调整.

策略3拆分堆栈箱组并调整其堆栈位置，进一步优化班轮横、纵向重量差.

若通过策略2调整后仍无法通过神经网络检验，则继续调整：

为了保证班轮堆栈的航线占用率，优先选择集装箱目的港最近的堆栈箱组拆分，避免新占用堆栈在过多港口被占用.

①纵向重量差调整.ⓐ前半部更重，更新Δw，从前半部选择1个目的港最近且重量大于Δw的堆栈箱组拆分，取出重量最接近Δw的若干个集装箱形成新的堆栈箱组，堆放在后半部第1个空堆栈；ⓑ后半部更重，类似地调整.

②横向重量差调整.上述调整时出现了新的堆栈箱组，为了不增加堆栈占用，首先采用策略2调整，若调整后可通过神经网络检验，则输出配载计划；若调整后仍不通过，则针对左、右半部按策略3中①方法类似调整.

4 算例研究

4.1 算例设计

根据国标GB/T 19283-2010，选取3艘不同尺寸类型(小型、中型、大型)的长江集装箱班轮进行算例研究，如表1所示.基于长江实际运输场景设计算例，考虑4条航线(表2)和3种不同的班轮装载率(表3).采用诸如S1-L1-C45的方式来表示不同算例，其中第1部分S1表示船型，第2部分L1表示航线，第3部分C45表示装载率.

表1 长江集装箱班轮信息Table 1 Information of container liner on the Yangtze River

表2 班轮航线Table 2 Container liner routes

表3 班轮装载率Table 3 Loading rates of container liner

4.2 算例求解

4.2.1 班轮航线配载结果

模型 SPM、LBM、CSM1及 CSM2均采用Gurobi 7.5.1求解.其中，模型SPM求解时其随机重量参数按平均箱重计算.HNS采用Python 3.6编程.所有算例均在一台4GB内存的笔记本电脑(Intel Core I7-5500U,2.40GHz)求解.

集装箱平均箱重分别设置为7 t、14 t和21 t.为了保证模型的求解效率，首先设置求解时间为60 s，当结果不理想或无法求解时，调整为600 s.对不同班轮而言，模型及算法的求解结果如表4～表6所示.在表4～表6中，f表示航线班轮堆栈占用数量；T表示算例求解时间(s)；gap表示模型SPM及算法HNS对应结果与下界模型(LBM)结果之间的偏差(%)；*表示无法在时间限制内求得结果.

从表4和表5中可以看出，由于模型SPM找到更多下界值且gap更小，其解的质量优于HNS.在求解时间方面，对于班轮S1，HNS表现更优；而对于班轮S2，模型SPM表现更优.从表6中可以看出，对于班轮S3，算例S3-L2-C85、S3-L3-C85及S3-L4-C85由于船舶体型更大、航线更长、班轮装载率更高，导致模型SPM无法在有限时间内求解.HNS求解所有算例且求解时间更短，其gap劣于模型SPM，但均小于4.5%.

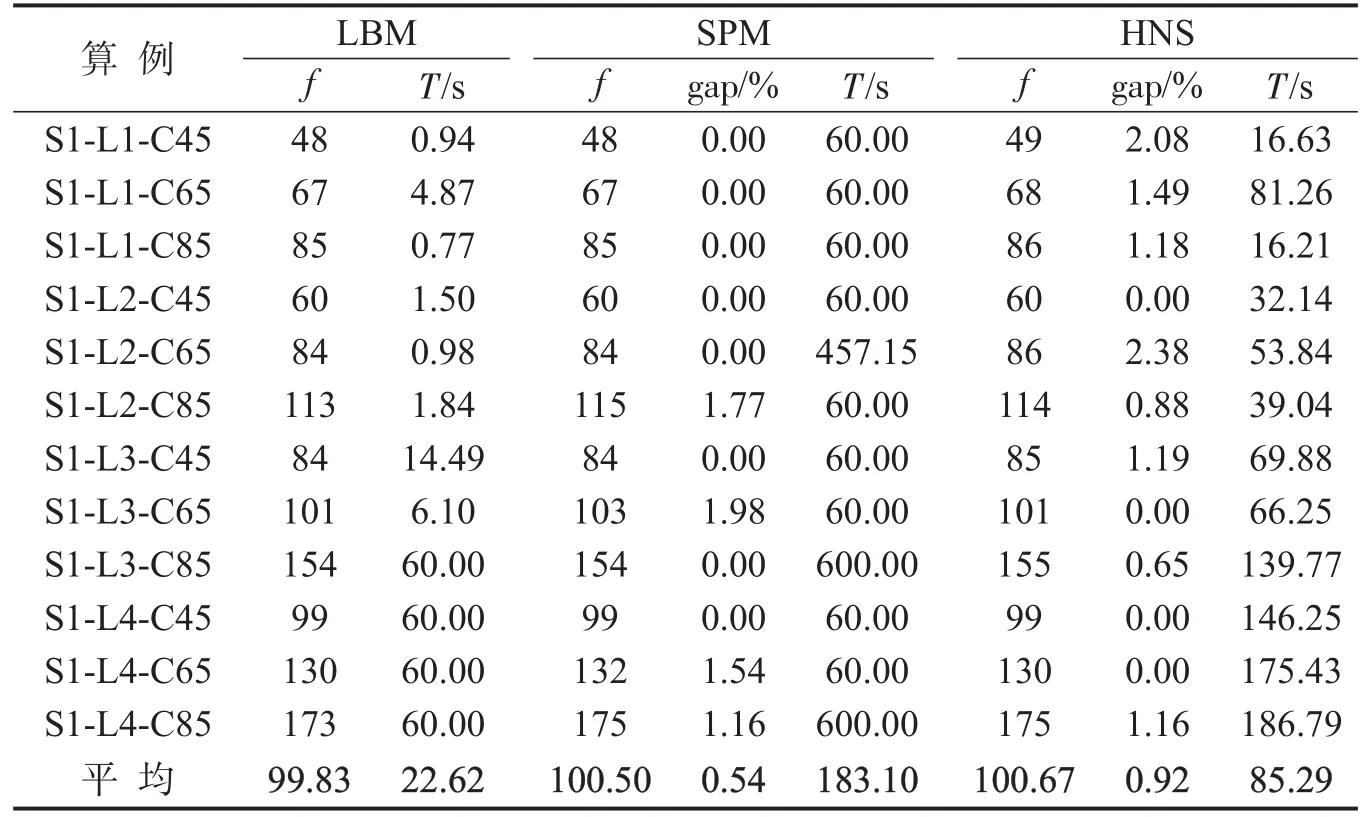
表4 班轮S1-模型及算法求解结果Table 4 Results of model and algorithm for liner S1

表5 班轮S2-模型及算法求解结果Table 5 Results of model and algorithm for liner S2

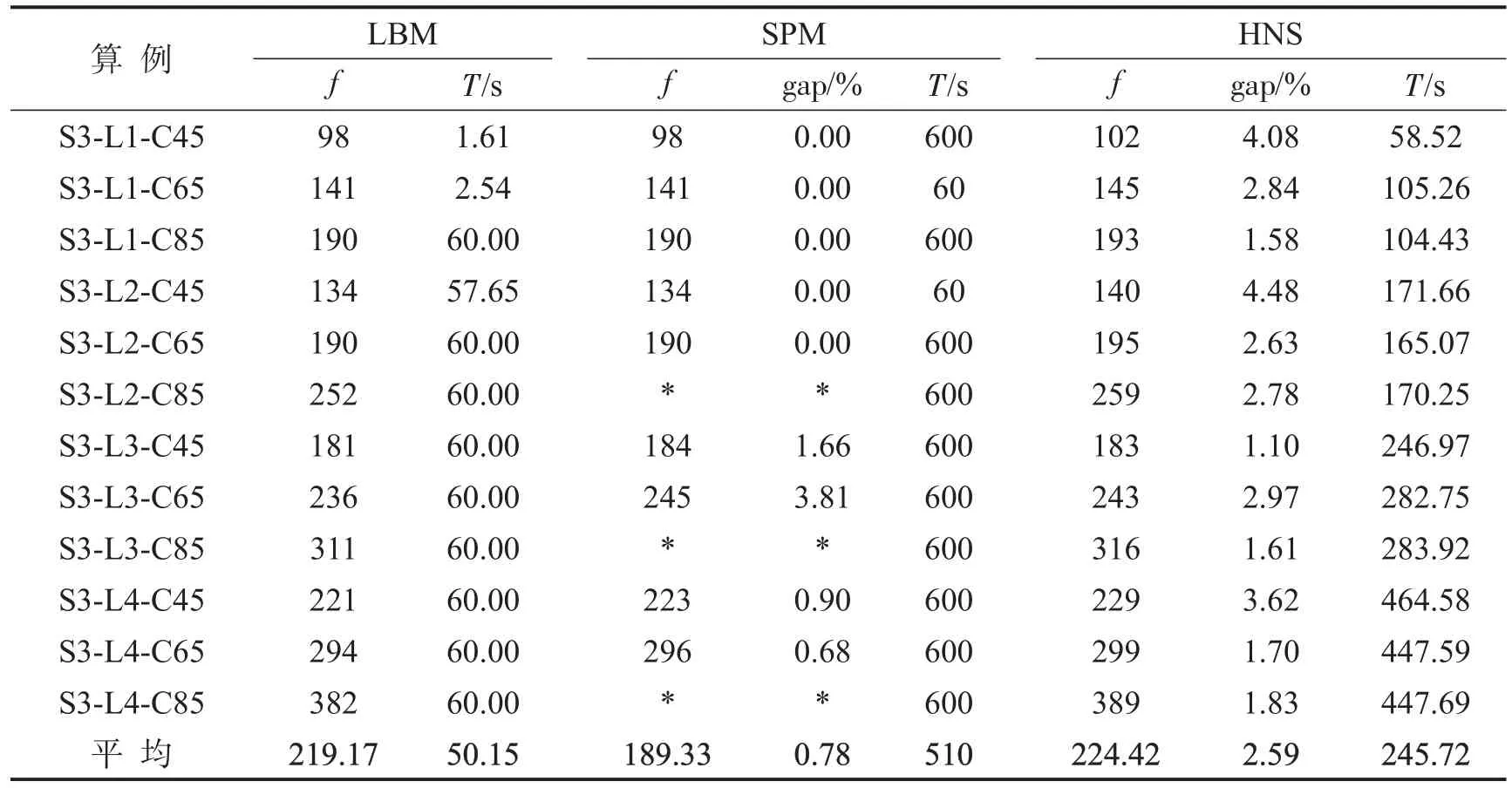
表6 班轮S3-模型及算法求解结果Table 6 Results of model and algorithm for liner S3

综上，在解的质量方面，模型SPM优于HNS，但由于未考虑不确定箱重对配载决策影响，无法保证当随机事件发生时配载计划仍可行；与模型SPM相比，HNS在求解时间和求解数量上更优且gap合理，尤其在求解大规模算例时表现更好.

4.2.2 蒙特卡罗仿真验证

为了进一步验证模型及算法的鲁棒性，采用蒙特卡罗随机模拟进行仿真验证.每个算例仿真1 000次，结果如图3所示.

从图3可以看出，由于未考虑不确定箱重对制定航线配载计划的影响，模型SPM的鲁棒性较差，仅有8个算例达到0.95的置信度水平，其他的通过率均不到0.8.而HNS均可达到0.95的置信度水平，满足模型SCPM的置信度要求.

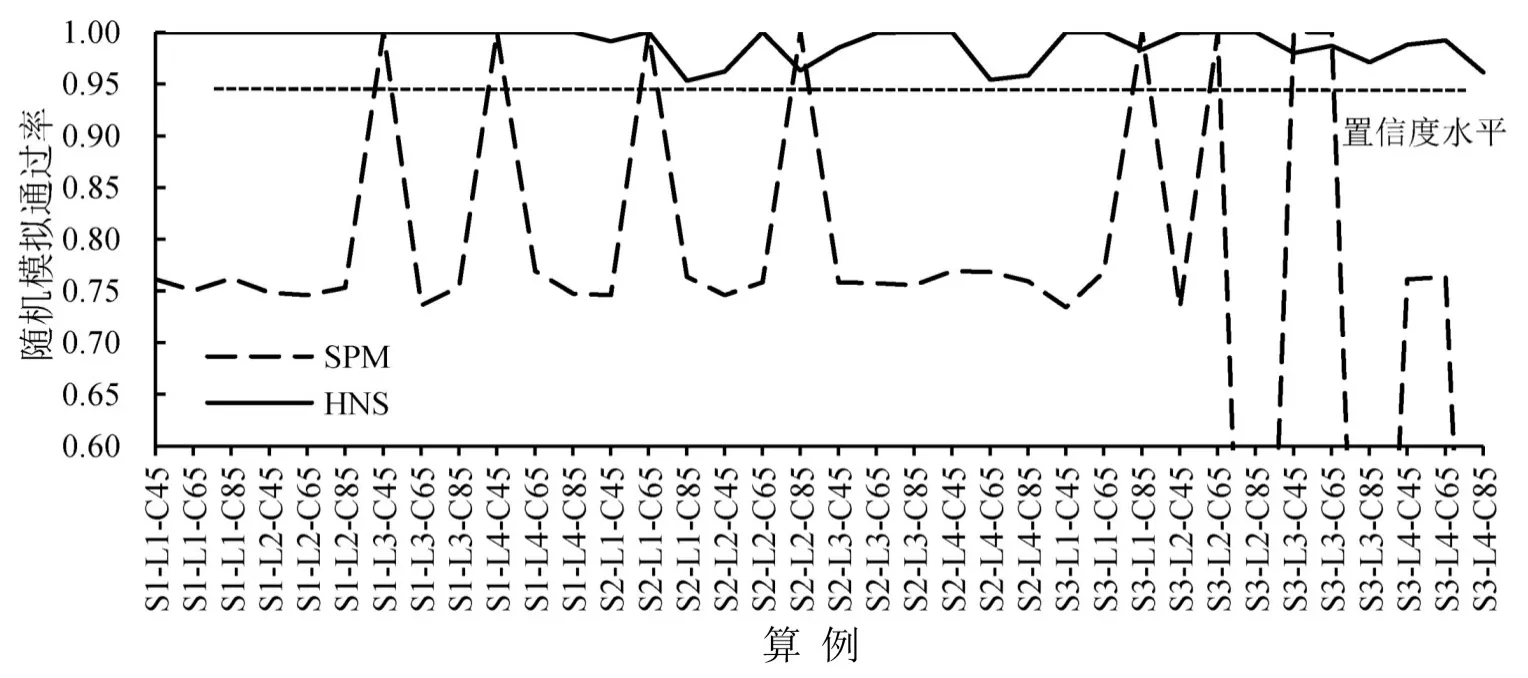
图3 蒙特卡罗随机模拟结果Fig.3 Result of Monte Carlo stochastic simulation

5 结论

本文考虑内贸箱不确定箱重，研究内河集装箱班轮航线配载决策问题.以最小化航线班轮堆栈占用数量为目标，构建随机规划和随机机会约束规划模型.对于后者，设计混合邻域搜索算法实现求解.算例研究表明：随机规划模型虽然求解结果更优，但难以保证随机事件发生时配载计划仍可行，鲁棒性较差；混合邻域搜索算法在求解数量和求解时间上均更优，与下界值的偏差也在合理范围内，且可顺利通过蒙特卡洛仿真检验，鲁棒性较好.后续，将针对内河集装箱班轮运输中外贸箱箱量变化等不确定因素进行研究.

参考文献：

[1]AZEVEDO A,RIBEIRO C,SENA G,et al.Solving the 3D container ship loading planning problem by representation by rulesand meta-heuristics[J].International Journal of Data Analysis Techniques and Strategies,2014(6):228-260.

[2]DING D,CHOU M C.Stowage planning for container ship:A heuristic algorithm to reduce the number of shifts[J].European Journal of Operational Research,2015(246):242-249.

[3]AMBROSINO D,PAOLUCCI M,SCIOMACHENA A.A MIP heuristic for multi-port stowage planning[J].Transportation Research Procedia,2015(10):725-734.

[4]祝慧灵,计明军.集装箱船舶全航线配载优化模型与改进遗传算法[J].交通运输工程学报,2014,14(5):59-67.[ZHU H L,JI M J.Optimal model and improved genetic algorithm of containership stowage on full route[J]．Journal of Traffic and Transportation Engineering,2014,14(5):59-67.]

[5]AMBROSINO D,PAOLUCCI M,SCIOMACHENA A.Computational evaluation of a MIP model for multi-port stowage planning problems[J].Soft Computing,2017(21):1753-1763.

[6]ARAÚJO E J,CHAVES A A,NETO L L S,et al.Pareto clustering search applied for 3D container ship loading plan problem[J].Expert Systems with Applications,2016(44):50-57.

[7]DONG J X,LEE C H,SONG D P.Joint service capacity planning and dynamic container routing in shipping network with uncertain demands[J].Transportation Research Part B,2015(78):404-421.

[8]杨华龙,刘迪,夏秋.集装箱班轮多港挂靠循环航次舱位分配[J].重庆交通大学学报(自然科学版),2012,31(6):1248-1251.[YANG H L,LIU D,XIA Q.Slot allocation of container liner in multi-port call cycle voyage[J].Journal of Chongqing Jiaotong University(Natural Science),2012,31(6):1248-1251.]

[9]郭子坚,许松乔,王文渊,等.集装箱港口堆场箱位数的二阶段随机规划方法[J].哈尔滨工程大学学报,2013,34(12):1520-1523.[GUO Z J,XU S Q,WANG W Y,et al.The two-stage stochastic programming method for determining the number of flat containers in the portyard[J].JournalofHarbin Engineering University,2013,34(12):1520-1523.]

[10]ZHAO R Q,LIU B D.Stochastic programming models for general redundancy optimization problems[J].IEEE Transaction on Reliability,2003,52(2):181-191.