动态不确定性环境下的地铁车站应急疏散仿真建模

黄家骏，徐瑞华*，洪 玲，黄肇红

(1.同济大学道路与交通工程教育部重点实验室，上海201804；2.广州地铁集团有限公司线网管控中心客运管理部，广州510000)

0 引言

应急疏散仿真已经广泛应用于模拟突发事故情况下地铁车站乘客应急疏散过程，以评估不同应急预案合理性，对于提高车站应急处置水平、保障社会公共安全具有重要意义.相比其他建筑，地铁车站以其空间关系复杂、设施设备众多、客运组织要求高等特点，使得应急疏散仿真除了疏散行为建模[1]，更应关注实际疏散环境对乘客疏散过程的影响.

实际疏散环境具有动态不确定性，表现为：①乘客从常态服务流程的不同环节开始疏散，个人状态及初始环境各不相同；②车站应急预案是依据实时客流分布调整，而疏散环境会随之产生动态变化，使乘客疏散运动发生改变，如果处置不当，则可能诱发二次事故.乘客疏散运动的改变，反映为动态调整疏散行为及通往出口的全局疏散路径，又会引起周围客流分布的波动.因此，动态不确定性环境使得乘客疏散行为及流线错综复杂、难以预测.目前，学者主要考虑环境感知和信息传递过程，并运用博弈论[2]、启发式力学[3]、选择效用[4]等模型模拟了节点选择行为，以体现疏散行为的不确定性.但选择过程的执行条件被限制，难以模拟环境突变(如采取应急预案等)的情况.在全局疏散路径方面，一般采用“流线客流”模型[5-6]，即疏散流线或出行矩阵事先人工设置，且初始状态与常态服务无关.然而，对于复杂场景仍存在着设置工作繁杂、主观经验依赖强等缺点，无法体现动态不确定性环境，从而影响仿真结果的精度.

在动态不确定环境下，乘客疏散过程是从常态服务状态切换，并以安全出口为最终疏散目标，不断感知周围环境的动态信息，及时做出决策的过程.因此，本文将疏散过程分解为不同的疏散阶段，基于Agent构建考虑变更代价的疏散行为动态切换模型，以及时响应环境变化；考虑与常态仿真的衔接，提出全局疏散路径搜索方法，摒弃提前设置流线的方法，解决空间疏散流线不确定性的问题，进而完善地铁车站应急疏散仿真模型.

1 乘客应急疏散过程的特征分析

地铁车站安全疏散要求[7]当发生灾害事故时，需根据灾害情况和灾害发生位置组织乘客通过非灾害区域向最终安全区域疏散.其中，最终安全区域为空间足够大、灾害无法波及的区域，一般为站厅层非付费区(下文简称非付费区)出入口.以位于站台层的进站乘客为例，当发生灾害事故时，乘客正处于常态服务的某一流程(候车或前往候车区)中，其应急疏散过程描述如图1所示.

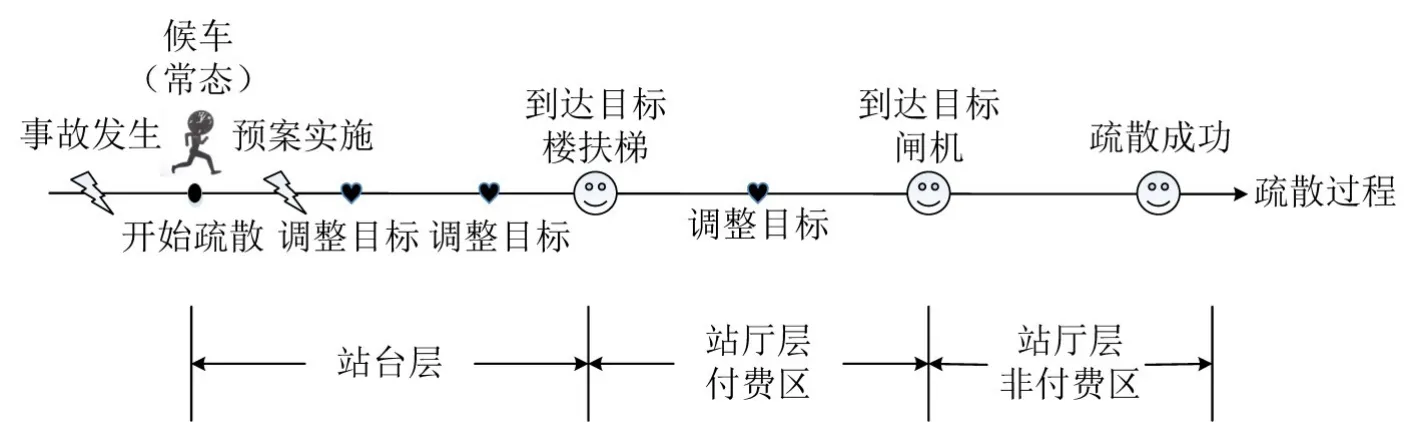
图1 站台层乘客分阶段疏散Fig.1 Staged evacuation process of passenger from platform

综上分析，各楼层/区域通往安全出口的楼扶梯、通道口、闸机(下文简称疏散设备)将乘客疏散过程划分为多个独立的疏散阶段.下一阶段的衔接是由当前阶段的目标疏散设备决定的.而目标疏散设备是乘客根据环境动态变化不断做出的决策及调整.其中，环境的变化包括预案实施、客流分布变化等，将导致乘客决策调整时机和次数不确定，全局疏散路径也无法预知.因此，在动态不确定性环境下，乘客应急疏散过程也具有动态不确定性的特征，表现为初始状态复杂、疏散行为的动态切换及空间疏散流线的不确定.这也是疏散仿真建模急需解决的问题.

2 基于Agent的疏散行为动态切换模型

乘客主要的疏散行为[8]包括就近、退避、原路返回、从众及引导等疏散行为.除了退避疏散行为是人类对突发事故的应激反应，可以用社会力模型[1]中排斥力进行描述，其余的疏散行为都是来源于乘客心理感受，可以用“效用值”进行描述.在应急疏散过程中，乘客遵循环境感知、目标决策及疏散运动的行为逻辑，可以通过Agent模型描述.

2.1 “环境感知”层建模

“环境感知”层是动态环境与乘客疏散行为间联系与互动的纽带.在时刻t，乘客r(r∈N*)所能感知到环境的动态信息INFOr(t)包括：Agent属性信息集，当前平面层的疏散设备状态信息集，以及事故信息集等3大类，即

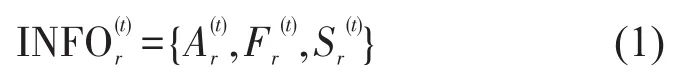
2.2 “目标决策”层建模

引入效用函数量化动态信息INFOr的影响，每个仿真步长选取效用值最高的疏散设备作为阶段目标，并动态切换就近、原路返回、从众及引导等4种疏散行为.

(1)就近疏散行为是乘客选择最近的疏散设备的行为，以乘客当前位置到疏散设备的距离构建效用函数为

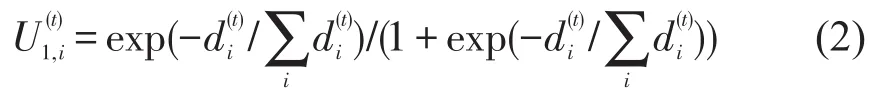
(2)原路返回疏散行为是乘客选择最为熟悉的疏散设备，以熟悉程度ci构建效用函数为

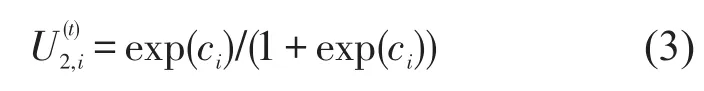
式中：如果疏散设备i被使用过，则ci=1；反之，ci=0.

(3)从众疏散行为是乘客选择使用人数最多的疏散设备，以使用人数构建效用函数为

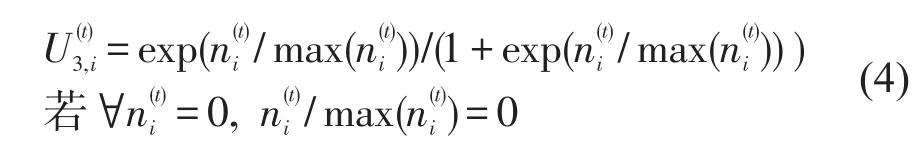
(4)引导疏散行为是乘客受导向/人员引导而选择指定的设备，以引导信息gi构建效用函数为

式中：如果乘客受引导疏散设备i的信息影响，即乘客当前位置p(t)在以引导信息位置为圆心、影响范围e为半径的圆内，则；反之，

上述4个效用函数独立不相关，因此乘客对于可选疏散设备i的总效用函数为这4种效用函数的权重加和，即

为减少仿真过程中因目标不断变更而导致疏散过程“左右摇摆”的情况，引入选择变更代价γ(t)，以描述乘客如果变更了目标，意味着之前的效用“无用”；乘客需要花费更多的时间趋向于新的目标，所产生的心理落差会阻碍其调整目标.公式为

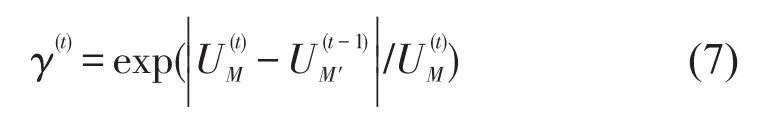
当时刻t，疏散设备M的效用最大，且与时刻t-1时选择的疏散设备M′不同，判断M是否已计算代价，如果已付出代价，则确认调整阶段疏散目标；反之，计算M的选择变更代价，重新权衡各疏散设备效用.

2.3 “疏散运动”层建模

乘客在明确阶段目标后，由“疏散运动”层负责规划走行路径并开始运动.因此，本层主要由A*算法和社会力模型构成：A*算法负责搜索当前位置到阶段疏散目标的最优路径，初步规划乘客在疏散阶段中的流线；社会力模型确定乘客实时速度、加速度等运动参数，并对具体路径进行局部调整，以模拟碰撞避让、退避疏散等行为.由于篇幅有限，A*算法和社会力模型的实现见文献[1]和[9]，本文不再赘述.

3 全局疏散路径搜索方法研究

3.1 基于常态服务流程的疏散空间衔接关系建模

疏散仿真的初始状态是由事故发生时每个乘客所处的常态服务流程事件所决定.在车站常态服务流程中，“通过楼梯”事件和“验票”事件的进入和离开地点不同，并表征了常态空间衔接关系{Lx→Ly},x,y∈N*,x≠y，即楼层/区域Lx(事件发生点，指向关系)指向楼层/区域Ly(事件结束点，被指向关系).

因此，针对不同类型服务流程的特点和流向，将“通过楼梯”事件和“验票”事件中涉及的常态空间衔接关系转置或不变，形成指向安全出口的疏散空间衔接关系集O，并以“疏散空间衔接关系—涉及疏散设备”({Lx→Ly-i})的形式记录.具体方法如下：

(1)对于进站客流，从第1个“验票”/“通过楼梯”事件开始，判断所涉及的疏散设备是否可以反向.如果为是，则转置事件中常态空间衔接关系，并记录涉及的疏散设备；否则，跳过.

(2)对于出站客流，从第1个“通过楼梯”/“验票”事件开始，记录涉及的疏散设备和常态空间衔接关系.

(3)对于换乘客流，在存在“通过楼梯”事件或“验票”事件的条件下，可近似看成是“出站服务+进站服务”的流程，分界点为“通过楼梯”事件是否发生在站厅层或“验票”事件结束在非付费区.如果上述条件均不满足，则相当于只有目的地为另一条线站台层的“出站服务”.

3.2 基于改进Dijkstra算法的全局疏散路径集搜索算法

基于疏散空间衔接关系集O，以经过楼层/区域最少(快速疏散)为目标，改进Dijkstra算法形成车站所有楼层/区域到非付费区的全局疏散路径集W.算法引入级数k来评估到非付费区距离：不与非付费区直接衔接的级数＞1，否则级数为1.关系集O中各元素的被指向关系将被赋予唯一的最小级数，则当前楼层/区域级数为k时，从级数k-1到级数1的各级可达元素均是当前楼层/区域起全局疏散路径的节点.具体流程(图2)如下：

Step 1疏散空间衔接关系集O的所有元素列入OPEN表中，清空CLOSE列表，初始化级数k=1.

Step 2判断OPEN表中各元素的楼层/区域被指向关系是否为非付费区.如果是，则将指向关系的楼层/区域记录到CLOSE列表，同时删除OPEN表中指向关系在CLOSE表的元素，并标识级数k.

Step 3判断CLOSE列表是否已经覆盖车站所有楼层/区域(除非付费区外)，如果是，转向Step4；否则，k=k+1并转向Step5.

Step 4输出全局疏散路径集W.

Step 5判断OPEN表中各元素的楼层/区域被指向关系是否为CLOSE表中k-1级的楼层/区域.如果是，则将指向关系的楼层/区域记录到CLOSE列表，并标识级数为k，同时删除OPEN表中指向关系在CLOSE表k级的相关元素.

Step 6结合集合O构建k到1级的楼层/区域衔接关系，更新至全局疏散路径集W，转向Step3.

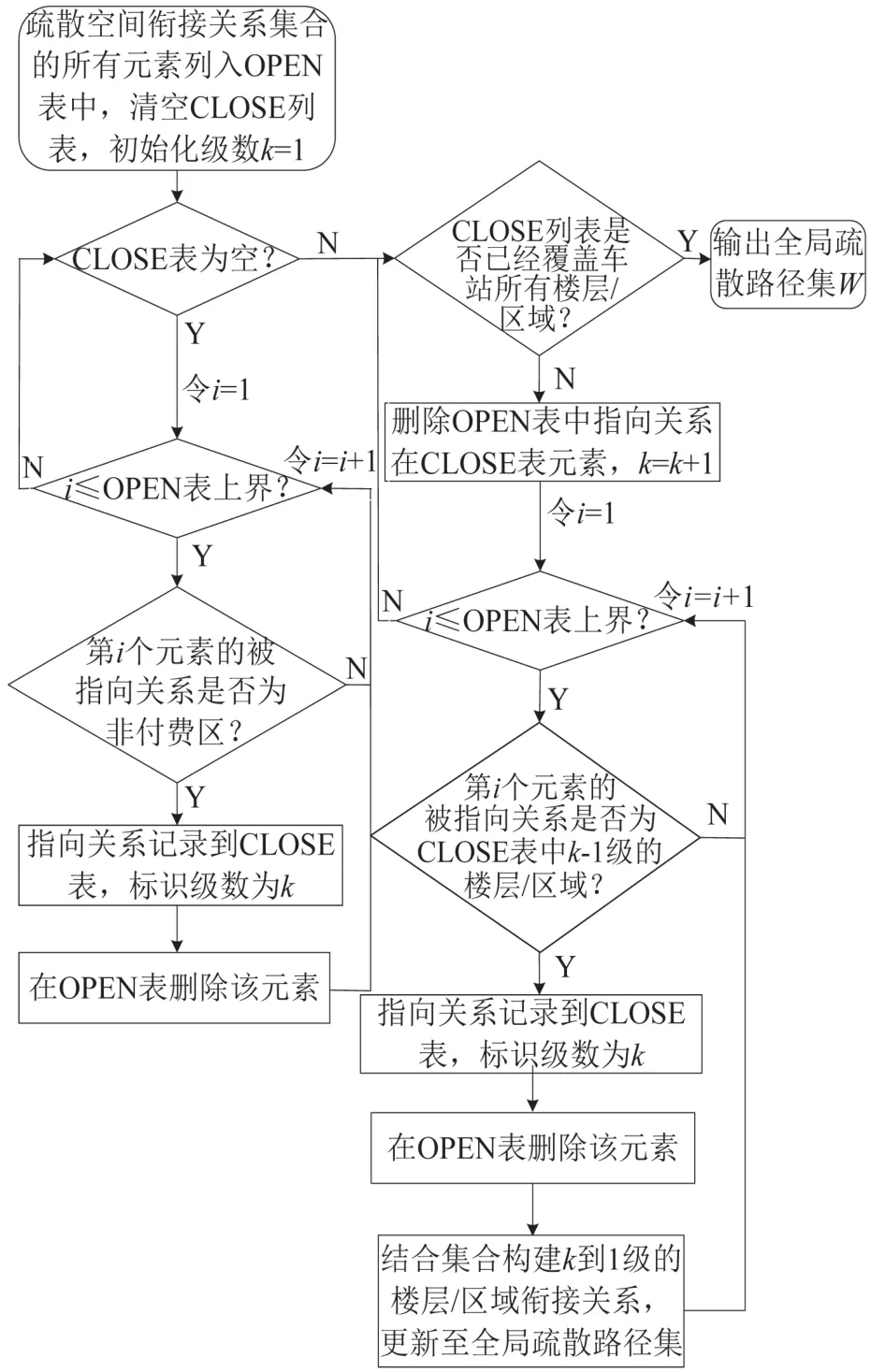
图2 全局疏散路径规划算法流程Fig.2 Global evacuation path planning algorithm flow

4 应急疏散仿真实验及分析

4.1 模型实现及突发事故场景设置

为了验证上述模型的可行性，在常态仿真软件Stapass[9-10]的基础上开发实现模型.软件中疏散仿真流程如图3所示.

以南宁轨道交通金湖广场站为例进行疏散仿真实验.金湖广场站为1、3号线通道换乘站，具体站内结构如图4所示.

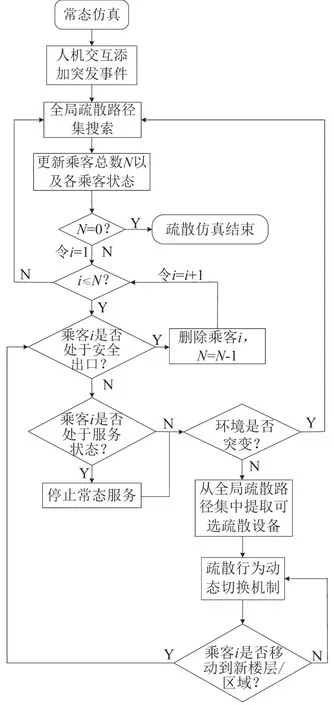
图3 Stapass中应急疏散仿真流程设计Fig.3 Design of emergency evacuation simulation process based on Stapass

假设突发事故场景为发生在3号线站厅层左侧楼扶梯附近的火灾，如图5所示，初始影响范围约为0.5 m.总疏散人数控制在1号线在站客流3 300±1%，3号线在站客流4 500±1%，要求发生事故后正处于或即将到达1号线站厅层、站台层的所有乘客疏散至1号线站厅层安全出口，其余客流疏散至3号线站厅层安全出口.

早高峰客流参数如表1所示.

表1 金湖广场站远期早高峰客流参数Table 1 Morning peak passenger parameters of Jinhu Plaza Station (人次/h)

4.2 不同应急预案仿真及结果分析

按规范[4]要求在突发事件发生后，车站立即关闭3号线站厅层最左侧的楼扶梯(图5中S1处)，作为预案1.位于3号线站台层的乘客仅能通过中间的扶梯(图5中S2处)和最右侧的楼扶梯(图5中S3处)疏散.

本预案总疏散时间为263 s，符合地铁安全疏散的要求.空间平均密度如图6所示，3号线站台层平均密度最大为7.15 ped/m2，站厅层平均密度最大为5.30 ped/m2.平均密度最大位置主要发生在S2处和S3处的楼扶梯区域，以及Z1处和Z4处的闸机区域(图6中圆圈部分).

S2处和S3处的楼扶梯区域平均密度较高是因为3号线站台层的客流仅能从这两个区域通过，造成了拥挤；Z4处的闸机区域平均密度较高是因为离S3处的楼扶梯最近，大部分乘客就近选择了通过Z4处闸机区域疏散；Z1闸机区域的平均密度较高是因为离突发事故位置较近，乘客发生了退避行为而拥挤于Z1闸机区域.

图4 金湖广场车站示意图Fig.4 Jinhu Plaza Station structure

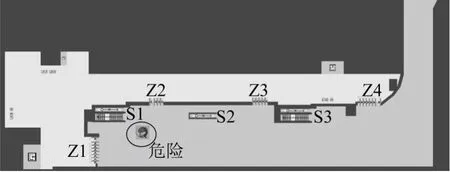
图5 突发事故场景示意图Fig.5 Incident scene

图6 3号线空间平均密度图(关闭楼扶梯)Fig.6 The average density of space in Line 3(the stairs in S1 were closed in Case 1)

对本预案中所有乘客采取的疏散行为(除退避行为之外)变更次数和比重进行统计，并与文献[8]中的调查结果对比，如图7所示，1～4次变更疏散行为的乘客较多，合计占77.4%，和调查结果(84%)基本接近，验证了模型实现乘客疏散行为的动态切换.

图7 不同疏散行为变更次数的乘客比重Fig.7 The proportion of times of evacuation behavior changing

考虑到Z1闸机区域的平均密度过大影响S3处的乘客快速疏散，在维持3号线站厅层最左侧的楼扶梯关闭后30 s内，在通道处增加引导标识，如图8所示，作为预案2.标识影响范围设定10 m，引导S3处乘客通过换乘通道前往1号线站厅疏散，并与预案1仿真结果比较.

本预案总疏散时间为251 s，符合地铁安全疏散的要求，比原预案降低约12 s.增加引导标识后的空间平均密度如图8所示，3号线站台层和站厅层平均密度最大值保持不变，但是和原疏散方案相比，在通道上的密度有所增加，而Z4处的闸机区域高密度范围减少，通过人数也减少，如图9所示.可见引导标识使得客流分布发生了变化，在一定程度上提高了疏散效率.

图8 3号线空间平均密度图(增加引导标识)Fig.8 The average density of space in Line 3(the guide was added in Case 2)

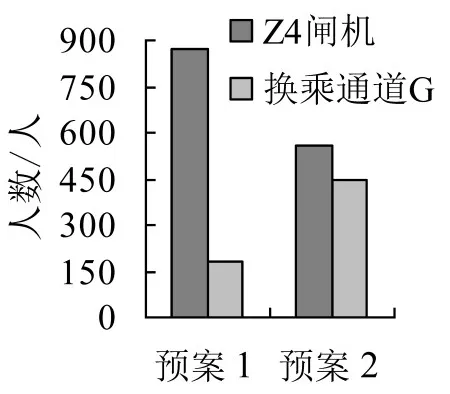
图9 2种应急疏散预案在关键位置通过人数比较Fig.9 The comparison of numbers of people passing key locations

5 结论

动态不确定性环境使乘客疏散过程具有初始状态、疏散行为、全局疏散路径不确定等问题.本文基于Agent模型提出疏散行为动态切换模型，并引入选择变更代价解决了动态环境下乘客因目标变更而产生的“左右摇摆”现象；考虑与常态仿真衔接，分析常态服务流程构建疏散空间衔接关系集；在此基础上以快速疏散为目标，引入级数并改进Dijkstra算法解决了全局疏散路径不确定的问题；结合Stapass软件设计了疏散仿真流程，并开发实现及案例验证.结果表明，模型具有可行性，并能够模拟动态不确定性环境下乘客的疏散过程.此外，模型摒弃了流线设置，并实现了仿真过程中随时干预环境的功能，提升了仿真精度，增加了实用性.但是，模型中“目标决策”层的决策过程建模需进一步深化，以贴合乘客实际选择过程.

参考文献：

[1]HELBING D,FARKAS I,VICSEK T.Simulating dynamical features of escape panic[J].Nature,2000,407(6803):487-490.

[2]李得伟.城市轨道交通枢纽乘客集散模型及微观仿真理论[D].北京:北京交通大学,2007.[LI D W.Modeling and simulation of microscopic pedestrian flow in MTR Hubs[D].Beijing:Beijing Jiaotong University,2007.]

[3]屈云超,高自友,李新刚.考虑从众效应和信息传递的行人疏散建模[J].交通运输系统工程与信息,2014,14(5):188-193.[QU Y C,GAO Z Y,LI X G.Modeling and simulating herding behavior and information spreading process in pedestrian flow[J].Journal of Transportation Systems Engineering and Information Technology,2014,14(5):188-193.]

[4]马洁,徐瑞华,李璇,等.地铁车站乘客疏散出口选择行为仿真建模[J].同济大学学报(自然科学版),2016,44(9):1407-1414.[MA J,XU R H,LI X,et al.Simulation modeling of pedestrian exit selection in evacuation process of rail transit station[J].Journal of Tongji University(Nature Science),2016,44(9):1407-1414]

[5]KISKO T M,FRANCIS R L,NOBEL C R.Evacnet4 user’s guide[M].University of Florida,1998.

[6]STAHL F I.BFIRES-II:a behavior based computer simulation of emergency egress during fires[J].Fire Technology,1982,18(1):49-65.

[7]全国公共安全基础标准化技术委员会(SAC/TC 351).地铁安全疏散规范(GB/T 33668-2017)[S].北京:中国标准出版社,2017.[China National Public Safety Fundamental Standardization Technical Committee(SAC/TC 351).Code for safety evacuation of metro(GB/T 33668-2017)[S].Beijing:Standards Press of China,2017.]

[8]洪玲,徐瑞华,段晓英.基于动态切换的城市轨道交通车站应急疏散模型[J].同济大学学报(自然科学版),2016,44(1):87-94.[HONG L,XU R H,DUAN X Y.Emergency evacuation model of urban rail transit station based on dynamic switching pattern[J].Journal of Tongji University(Nature Science),2016,44(1):87-94.]

[9]GAO P,XU R,ZOU X.A modified heuristic search algorithm for pedestrian simulation[C].Plan,Build,and Manage Transportation Infrastructure in China.ASCE,2008.

[10]高鹏,徐瑞华.城市轨道交通车站客流仿真中的事件驱动模型[J].系统工程理论与实践,2010,30(11):2121-2128.[GAO P,XU R H. Event-driven simulation model for passenger flow in urban mass transit station[J]. Systems Engineering-Theory &Practice,2010,30(11):2121-2128.]