多元数据下的公交站点客流不确定性分析

柳伍生，周向栋，谭 倩

(1.长沙理工大学交通运输工程学院，长沙410004；2.中南大学交通运输工程学院，长沙410075)

0 引言

传统的公交客流数据采集主要通过人工问卷调查法获取，需要耗费大量的人力、物力，且样本数量少、精度不高.近年来，GPS系统、公交IC卡数据及地铁数据的广泛应用，为公交乘客出行特征分析、公交出行OD获取提供了新的思路[1].

国外对结合大数据的公交客流OD研究较早，也相对成熟.James等[2]依托大数据分析实现了对纽约市的公交客流OD推导.Zhao等[3]针对地铁—地铁，地铁—公交的两类出行链做了公交客流推导，Cui等[1]对于不同规模的公交客流研究了相应的推导方法.国内对于公交客流OD的推导研究较晚.胡郁葱等[5]通过IC卡数据挖掘技术获取了公交OD矩阵.胡继华等[6]提出结合出行链的IC卡公交客流研究方法.李海波等[7]提出了公交IC卡与AVL数据相结合的公交客流OD研究方法.综上国内学者研究主要集中与单个IC卡数据的下车站点的推导问题.

实际上，复杂的公共交通环境及乘客的个体随机出行特征，使得上下车客流往往在一个区间范围内波动.大数据背景下，对同一对象的观测值是多个的，利用长时间观测的多个数值分析公交客流，并未得到学者足够的重视[8].给定一个区间客流值给决策者提供更好地支撑，也更有实际作用.本文通过区间不确定性理论与交通大数据相结合，以出行链的思想，对1天刷卡次数行为进行分析，结合乘客出行站数和乘客个体出行特征，以公交IC卡数据和GPS数据为基础，对公交客流区间OD推导方法进行系统研究，并以深圳市公交数据为实例进行分析研究.

1 公交数据处理与上车站点的确定

1.1 公交数据处理

研究数据来源于深圳市公交IC卡和公交GPS数据，公交线路及站点基础数据，需要对这些数据进行预处理，剔除不需要的数据，筛选得到研究需要的公交基础数据，如表1所示.依据车辆编号与车牌号之间的对应关系，终端ID与车牌号之间的对应关系，得到公交融合数据，包括IC卡编号、车辆编号、终端ID、刷卡时间与接受时间、车辆GPS经纬度和站点经纬度等.

表1 公交基础数据Table 1 Bus basic data

1.2 基于时间匹配的上车站点的确定

上车站点的确定可通过2步数据融合得到，第1步为GPS数据与静态的公交站点数据的融合，得到车辆到达各个站点的时间；第2步为车辆到达各个站点的时间与IC卡刷卡数据的融合，得到各个站点在各个时间的刷卡数据，如图1所示.

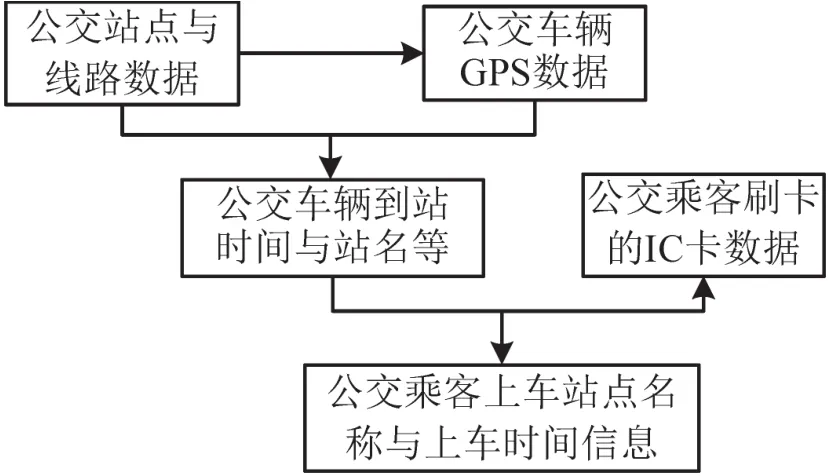
图1 基于公交IC卡数据和GPS数据的上车站点识别Fig.1 Based on bus IC card data and GPS data on the site identification

Step 1公交GPS数据与站点静态数据匹配方法.

(1)利用公交GPS经纬度坐标与站点经纬度坐标于MySQL数据库中做笛卡尔积，并进行行车方向的判断(上行或下行).

(2)运用SQL查询语句筛选得到站点经纬度坐标50 m范围内公交GPS经纬度坐标，选取2个离公交站点最近GPS经纬度Si(xi,yi),Si+1(xi+1,yi+1)，相应的时间分别为Ti,Tj.Si，Si+1分别为行车方向上的前后两个经纬度坐标点.

(3)到离站时间判断.公交站点经纬度坐标为Pi(xi,yi)，若Pi位于Si，Si+1连接线之间，如图 1(a)所示，则认定相应的Ti,Tj分别为到站时间和离站时间；若Pi位于Si之前，如图1(b)所示，则认定Ti为离站时间，Ti-30 s为到站时间；同样，若Pi位于Si+1之后，如图1(c)所示，则认定Tj为到站时间，Tj+30 s为离站时间.

Step 2公交IC卡数据和GPS数据相结合的上车站点识别方法.

对于公交IC卡任意刷卡记录i，若刷卡记录i的刷卡时间tbi和一对进离站时间区间(tak,tck)满足式(1)，则该时间区间所在站点Sk即为记录i的上车站点.

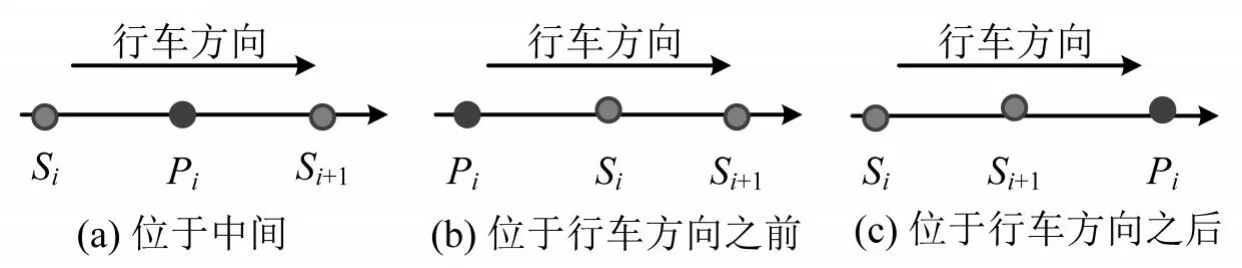
图2 公交站点经纬度与GPS数据位置关系判断Fig.2 Judgment of the relationship between latitude and longitude of the bus station and GPS data location

式中：tak为公交车到站时间；tck为公交车离站时间.

实际公交运营中，对于公交多换乘站点，大量公交车同时在站点排队，导致存在站前站后刷卡现象，为增加认知精度，对进离站时间区间(tak,tck)进行弹性改进.

式中：φa为公交车到站弹性时间；φc为公交车离站弹性时间；φa，φc皆大于0.

2 区间不确定性理论与公交刷卡行为分析

2.1 区间不确定性理论

区间不确定性理论在数学上叫做区间数优化方法[8].通过一个参数取值的波动区间集合，对该区间集合进行优化即区间数优化.区间数优化方法一般以概率大小来确定不确定约束及控制的满意程度，不确定性目标函数的性能由多个约束保证，具有更好的灵活性和柔性.区间数优化方法分为3类：①基于区间数序关系的线性区间数优化，②基于最大最小后悔准则的线性区间数优化，③非线性区间数优化.

本文采用第3类非线性区间数优化方法，对于1组数据集合A=[μ1,μ2,μ3,…,μn]，从小到大排列，得到n个数据排列新集合，采用统计学中置信区间概念进行取值优化，通过专家经验法和实际数据分析，设显著性水平β，置信水平(1-β)×100%，=1-β，A1和A2为置性区间的两个上下界值，得到n个数据的区间集合[A1,A2].

2.2 上车刷卡行为分析

实际生活中公交乘客存在1天多次的刷卡行为，对1天刷卡次数1～4次的行为进行了分析，如表2所示，对于刷卡次数超过4次以上的少数情况忽略不计.

结合现实生活中一卡多刷的现象，提出和人共乘行为的假设：如果同一卡号的连续2次以上的刷卡记录的时间间隔小于对应站点间的行程时间，则后几条刷卡记录判定为和人共乘记录.假设和人共乘人员出行路径一致，即两者下车站点一致(假设1).

结合刷卡行为分析，结合实际运营中，公交乘客于同一站点间换乘，提出换乘假设：乘客下次刷卡站点位于当次乘客刷卡上车站点的下游站点(当次乘客线路行驶方向向下)且时间间隔为当次乘车所用时间波动区间内，则乘客当次乘车的下车站点为下次乘车上车站点(假设2).

3 下车站点推导及上下车区间客流的确定

3.1 下车站点推导模型

现有公交IC卡信息中无乘客下车信息，依本研究上车站点确定方法，可得乘客上车站点，下车站点通过乘客个体出行特征和乘客出行距离相结合的站点吸引概率模型来进行推导.

乘客出行站数分布具有一定的统计分布规律，本文采用泊松分布，即

考虑乘客个体特征，在任意站点i上车的特定乘客q，在线路l下游任意站点j下车，定义如下：

(1)下游站点集合Eq，运行方向下线路l在上车站点i的下方所有站点集合.

(2)高频站点集合Fq，下游站点集合中，乘客上下车频次高的站点.由于每个乘客的高频站点各不相同，Fq为乘客前n天上车站点记录的集合与Eq的交集.Fq中的站点需满足条件：乘客在该站点的前n天上车次数高于数值x.x的取值由前n天的时间跨度所决定，从而得到高频站点集合Fq.依据高频站点性质分类为商业中心站点集合F1q、学校中心站点集合F2q、居住中心站点集合F3q、办公中心站点集合F4q，其数学关系为F1q⊂Fq，F2q⊂Fq,F3q⊂Fq,F4q⊂Fq,F1q+F2q+F3q+F4q=Fq.

(3)换乘枢纽站点集合Gq，乘客下次乘车的上车站点与当次乘车的下车乘车的交集.

表2 1天中不同刷卡次数行为分析Table 2 Analysis on the behavior of different scrap cards in one day

这3大集合的数学关系为：Gq⊂Fq⊂Eq，其中，Gq最多包含1个元素，Gq,Fq可为空集.

若Gq非空，则站点j对特定乘客q的站点吸引权为

若Gq为空，Fq非空，则站点j吸引权重为

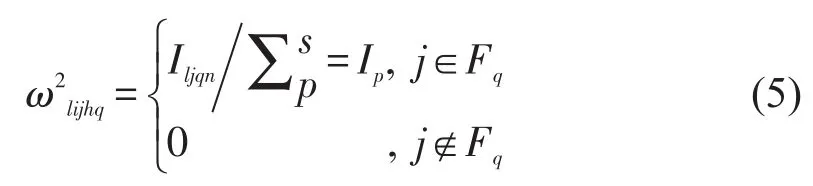
式中：Iljqn为在线路l上，特定乘客q在前n天在站点j的上车次数；s为高频站点集合包含的站点个数；p为s个高频站点的任意站点；Ip为乘客q在高频站点p的近期上车次数.

若Gq为空，Fq为空，则站点j吸引权重为

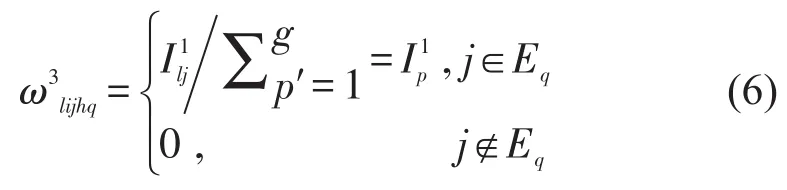
综上，考虑乘客个体特征和乘客出行距离，线路l上在站点i上车的特定乘客q，经过h个站点在站点j下车的概率为

式中：plijhq为线路l上在站点i上车的特定乘客q，经过h个站点在站点j下车的概率；为线路l上在站点i上车的特定乘客q，经过h个站点在站点j下车的出行距离概率；ωlijhq为在线路l上，在站点i上车的特定乘客q，经过h个站点在站点j下车的站点吸引权重.

3.2 下车站点推导流程

依据本文上车站点确定方法，得到线路l上的每条公交IC卡刷卡记录的上车站点，再依据乘客前n天公交IC刷卡记录，其前n天的上车站点推导仍用本文推导方法，乘客下车站点的推导算法流程如图3所示.

图3 下车站点推导流程图Fig.3 Get off the site to derive the flow chart

3.3 上下车区间客流的推导

线路l前n天k个站点的公交IC卡刷卡数据为：天数集合N={1,2,…,n}，站点数集合K={1,2,…,k}.依据上车站点识别方法，下车站点推导算法得到线路l上各站点的当天上下车人数集合分别为S={αi,i=1,2,…,k} ，X={λj,j=1,2,…,k} ；线路l上前n天的各站点的上下车人数集合分别为S1={αxi,x=1,2,…,n,i=1,2,…,k},X1={λxj,x=1,2,…,n,j=1,2,…,k} ；对集合S1，X1中的各站点的前n天上下车人数进行从小到大重新排列得到新集合S2=

由于前n天第k个站点每天的上下车人数集合中某些元素不符合常规，不符合该站点下车人数规律的变化，结合区间不确定性理论，利用区间数优化理论，对新集合S2，X2进行区间取值优化，本文采用统计学中置信区间概念进行取值优化，通过实际调查和专家经验法，分别设上下车显著性 水 平 为β1，β2；置 信 水 平 分 别 为，Yi1和Yi2，Zj1和Zj2分别为两个置性区间的两个上下界值.则前n天k个站点的每天上下车客流区间值分别为[Yi1,Yi2]，，从而得到线路l上前n天的各站点的上下车人数区间数集合分别为

4 实例分析

4.1 上车客流区间推导

以深圳市21路公交2015年11月13～12月25日全天单向(紫薇阁总站—中山园场站)的IC卡刷卡数据为例，对其中30天工作日每日的公交IC卡数据进行上车站点确定，共63 891条数据.通过计算分析，弹性时间φa和φc，分别取进站前和出站后的站间行驶时间的1/5，即依据上车站点确定法则，通过编程匹配得到98.2%的数据确定上车站点，1.4%的数据需人工匹配确定上车站点，得到每天各站点工作日的上车人数.依据上车站点的确定数据和上车客流区间推导方法，取显著性水平β1=0.1.通过python数据预处理，R数据筛选分析处理，得21路公交2015年11月13日～12月25日期间工作日全天单向(紫薇阁总站—中山园场站)的各站点的上车客流区间数分布，如图4和图5所示.

4.2 下车客流区间推导

依据本研究下车站点客流推导流程法则，进行下车站点推导，高频站点集的频次约束不低于3次，乘客近期出行的历史数据为2015年11月13日～12月25日，判断出下车站点的数据总数共61 610条，占确定的上车站点数据的96.6%，其部分计算结果和下车站点客流区间如表3和图6所示.

图4 上车站点确定结果汇总图Fig.4 On the site to determine the results of the summary map

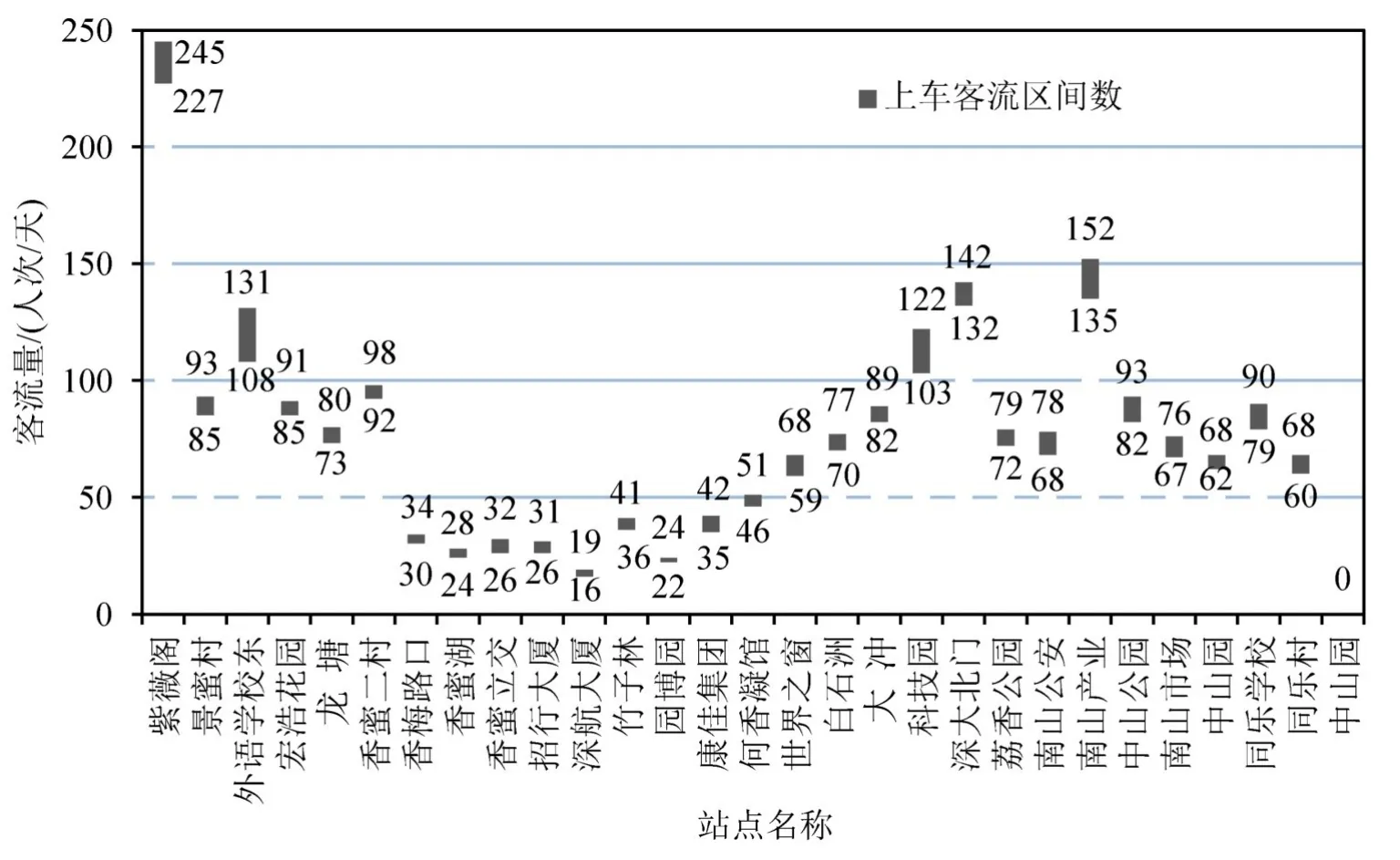
图5 上车客流区间分布图(单向)Fig.5 On the bus passenger flow distribution map(one way)

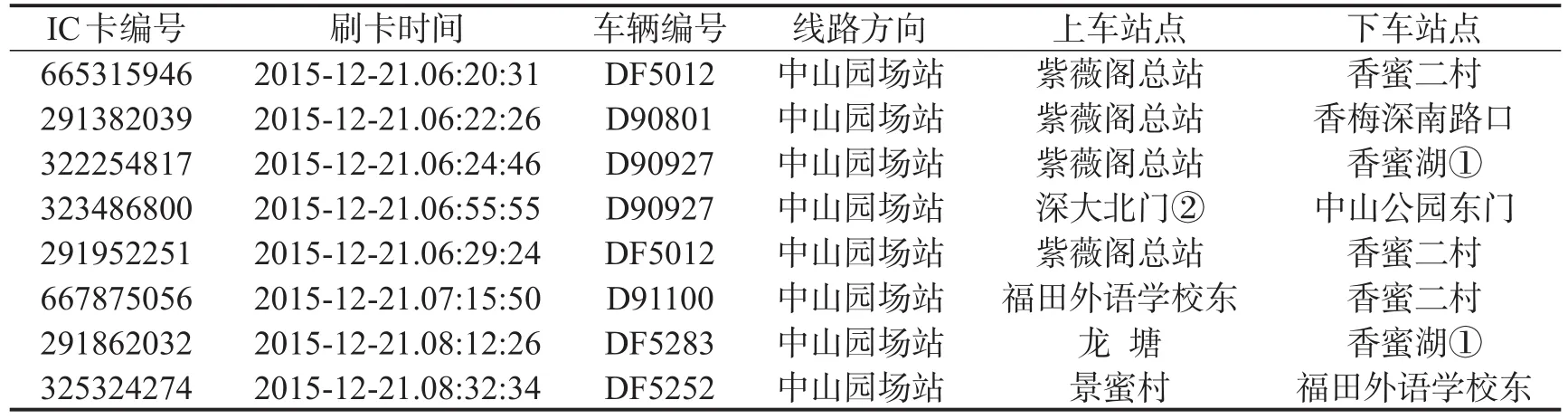
表3 算法部分计算结果Table 3 The algorithm part calculates the result

图6 下车客流区间分布图(单向)Fig.6 On the bus passenger flow distribution map(one way)

5 结论

结合交通大数据和区间不确定性理论，以公交IC卡和GPS海量数据为基础，改进上下车站点推导方法，增加进离站时间弹性时间，提高了上车站点识别率；依据乘客个体特征，对乘客刷卡行为进行分析，提出乘客出行线路的多种组合模式；结合既有的下车站点距离吸引概率推导模型，提出增加各个站点吸引权重，得到乘客下车站点推导模型.最后考虑海量数据在同一对象上具有多个数据，加入区间不确定性理论，以置信区间区间数优化方法得到上下车站点的公交客流区间，有利于决策者在分析客流时的客观性.在此基础上，以深圳市21路公交IC卡和GPS数据为例进行实例分析，验证了方法的有效性.

对于乘客上下车客流区间值分布研究，得到每天的客流区间分布，对于每个时段的客流区间分布将是下一步研究重点，同时将通过可靠的居民出行OD数据结合交通大数据，得到公交交通出行区间OD.

参考文献：

[1]CUIA.Bus passengerorigin-destination matrix estimation using automated data collection system[D].Boston:Massachusetts Institute of Technology,2006.

[2]BARRY J J,NEWHOUSER R,RAHBEE A,et al.Origin and destination estimation in New York City with automated fare system data[J].Transportation Research Record,2002,18(17):183-187.

[3]ZHAO J H.The planning and analysis implications of automated data collection systems:Rail transit OD matrix inference and path choice modeling examples[D].Cambridge:Massachusetts Institute of Technology,2004.

[4]ALEX C.Bus passenger origin-destination matrix estimation using automated data collection systems[D].Cambridge:Massachusetts Institute ofTechnology,2006.

[5]胡郁葱,梁杰荣,梁枫明.基于IC卡数据挖掘获取公交OD矩阵的方法[J].交通信息与安全,2012,30(4):66-70.[HU Y C,LIANG J R,LIANG F M.A way to get bus regional OD matrix based on mining IC card information[J].Journal of Transport Information and Safety,2012,30(4):66-70.]

[6]胡继华,邓俊,黄泽.结合出行链的公交IC卡乘客下车站点判断概率模型[J].交通运输系统工程与信息,2014,14(2):62-67.[HU J H,DENG J,HUANG Z.Trip-chain based probability model for identifying alighting stations of smart card passengers[J].Journal of Transportation Systems Engineering and Information Technology,2014,14(2):62-67.]

[7]李海波,陈学武,陈峥嵘.基于公交IC卡和AVL数据的客流OD推导方法[J].交通信息与安全,2015,33(6):33-39.[LI H B,CHEN X W,CHEN Z R.Amethod for estimating origin-destination matrix of public transit based on smart card and AVL data[J].Journal of Transport Information and Safety,2015,33(6):33-39.]

[8]周和平,全维杰,杨启福,等.基于区间情景的不确定性OD反推模型与算法[J].系统工程,2013,31(10):75-80.[ZHOU H P,QUAN W J,YANG Q F,et al.Uncertain optimization model and algorithm of estimating origin-destination matrices based on interval scenarios[J].Systems Engineering,2013,31(10):75-80.]