突发环境下城市道路网关键路段集识别

李彦瑾，罗 霞

(西南交通大学 交通运输与物流学院，成都610031)

0 引言

自然灾害、交通事故等突发事件具有随机性强、涉及面广和负扩散效应显著等特点.当城市道路网中单条或多条脆弱路段出现突发事件时，极易引发相关路段连锁排队，造成大面积的交通拥堵.这不仅阻碍了受困人群的疏散，而且延误了救援人员的到达和应急物资的输送.因此，合理运用路网脆弱性分析方法，识别突发环境下影响路网运行的关键路段集合，对于道路交通防灾减灾规划和灾后应急救援资源调度等有重要的实践意义.

关键路段的识别是路网脆弱性分析的基础[1]，传统研究思路为：先构建关键路段识别指标，运用“遍历法”轮流从路网中删除某一路段，再依据识别指标的变化情况来衡量该路段对整个路网的影响.沿用这一思路，Berdica[1]、D’Este[2]、Jenelius[3]、Sullivan[4]等分别采用路段饱和度、连通性、路段重要度和网络鲁棒性指数等识别关键路段.这类方法虽可直接比较不同拓扑结构的道路网络，但对于大规模路网，其计算效率较低，误判可能性较大[5-8]；对此，Wang[5]、Farahani[6]等采用对偶算法压缩模型可行域；张玺[7]、李彦瑾[8]等运用鲁棒性分析减少对关键路段的误判.

上述研究虽作出了积极地探索，但囿于均以单条路段为研究对象，不能理清多条路段同时失效时，路网与关键路段集之间的内在联系；另外，突发环境下的城市道路网一般拥有以下3个特征，也使得既有方法不能很好解决这类问题：

(1)突发事故涉及面广、传播速度快，在短时内可能造成路网中多条路段失效，失效路段构成一个路段集合；

(2)突发环境下，路网中的正常路段一般无法迅速消解拥堵，其道路通行能力限制会对整个路网的交通流分布产生重要影响[8]；

(3)突发事件的应急响应具有紧迫性，需及时制定救援策略，避免对关键路段的误判.

因此，为克服以上3个问题可能带来的不足，本文拟从路网特性分析入手，采用线性化手段，构建一个涵盖单条到多条路段失效的混合0-1规划模型，再以分支定界法获取可行解，并设计算例进行验证.

1 城市路网特性分析

对城市道路网进行拓扑分析时，一般采用原始法或对偶法.考虑到原始法能直观、简明地反映路网拓扑结构，且便于研究者分析网络效率，故本文选用原始法构建路网.

1.1 突发事件的特点

突发事件的主要特点是发生的随机性与影响的不可预知.

对于发生的随机性，采用鲁棒性分析方法，旨在从中观层面上得到不同路段失效后路网鲁棒性的变化情况.另一方面，由于负面效应越大的突发事件对路网的破坏力也越强，这反映在网络中则是失效路段数的增多，故本文尝试用失效路段数对突发事件的影响进行差异化评价.下面，先量化突发事件发生的随机性.

1.2 突发事件下的路网拓扑变化

暂不考虑交通流等因素，假定某条路段出现突发事件将立即导致路段失效，其拓扑变化如图1所示.

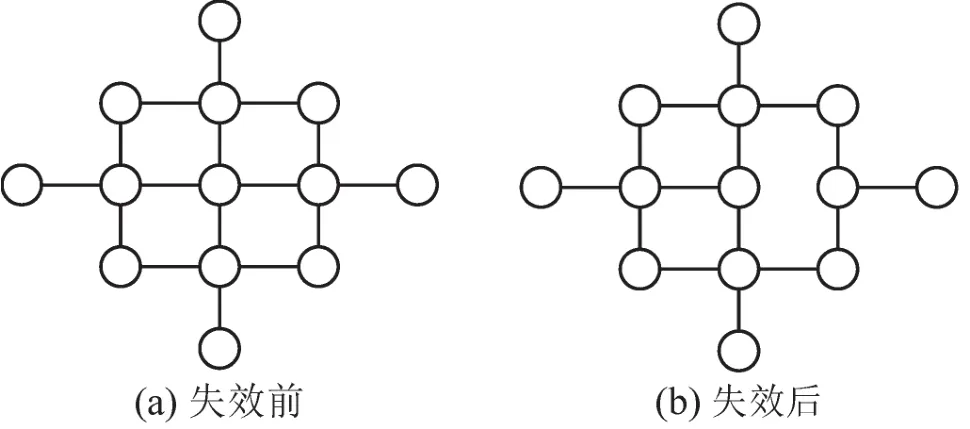
图1 路网拓扑形态变化Fig.1 Road network’topological morphological changes

进一步地，将突发事件视为对路网的一次随机攻击，则该环境下的路网拓扑变化可用鲁棒性方法进行评估[8-9].

1.3 城市道路网鲁棒性分析

路网鲁棒性是指路网在遭受随机或蓄意攻击时，保持正常运作的能力，由鲁棒性指标刻画.本文从中观层面选取：网络效率、最大连通子图2类与路段相关的鲁棒性指标进行分析.

(1)网络效率.

网络效率是利用节点间最短路的均值衡量路网的通行效率[9].若在路段失效前后其变化量ΔE越大，表明该路段对路网鲁棒性的影响越显著.ΔE计算公式为

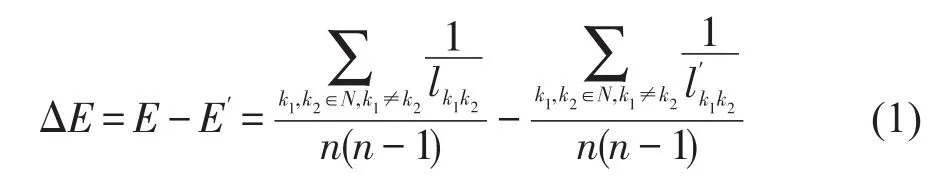
式中：E为网络效率；N为节点集合；n为路网节点总数；分别为路段失效前后连接节点k1，k2间的最短路.

(2)最大连通子图.

最大连通子图是指以最少的边把网络中尽可能多的节点连接起来的子图[9].其相对大小变化量ΔS反映了路网在遭受随机攻击后，拓扑结构发生的改变.ΔS计算公式为

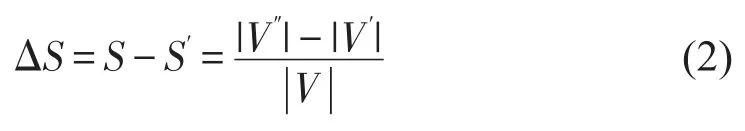
对于路网G(N,L)，N为点集合，L为边集合.采用遍历法，轮流去掉G(N,L)中的路段，分别计算其鲁棒性指标的变化量：ΔE和ΔS.然后，寻找出ΔE和ΔS均较大的路段，构成潜在关键路段集合L′(备选集).

注意：在不考虑路网交通流的条件下，潜在关键路段集L′可视为模型可行域的压缩.这既有助于简化模型求解规模，又能建立路网鲁棒性与关键路段识别指标间的联动关系.

接着，完成单条到多条路段失效后的路网关键路段集识别，以此评价不同类型突发事件对路网的影响.

2 关键路段集识别

本文将突发事件前后路网总阻抗的变化量作为识别指标[1-4,7-8]，研究起讫点(Origin-Destination，OD)需求固定的道路交通网络，并在潜在关键路段集L′的基础上，构建一般化的关键路段集识别模型.

2.1 符号说明

对路网G(N,L)进行建模，模型运用的符号变量及其意义如表1所示.

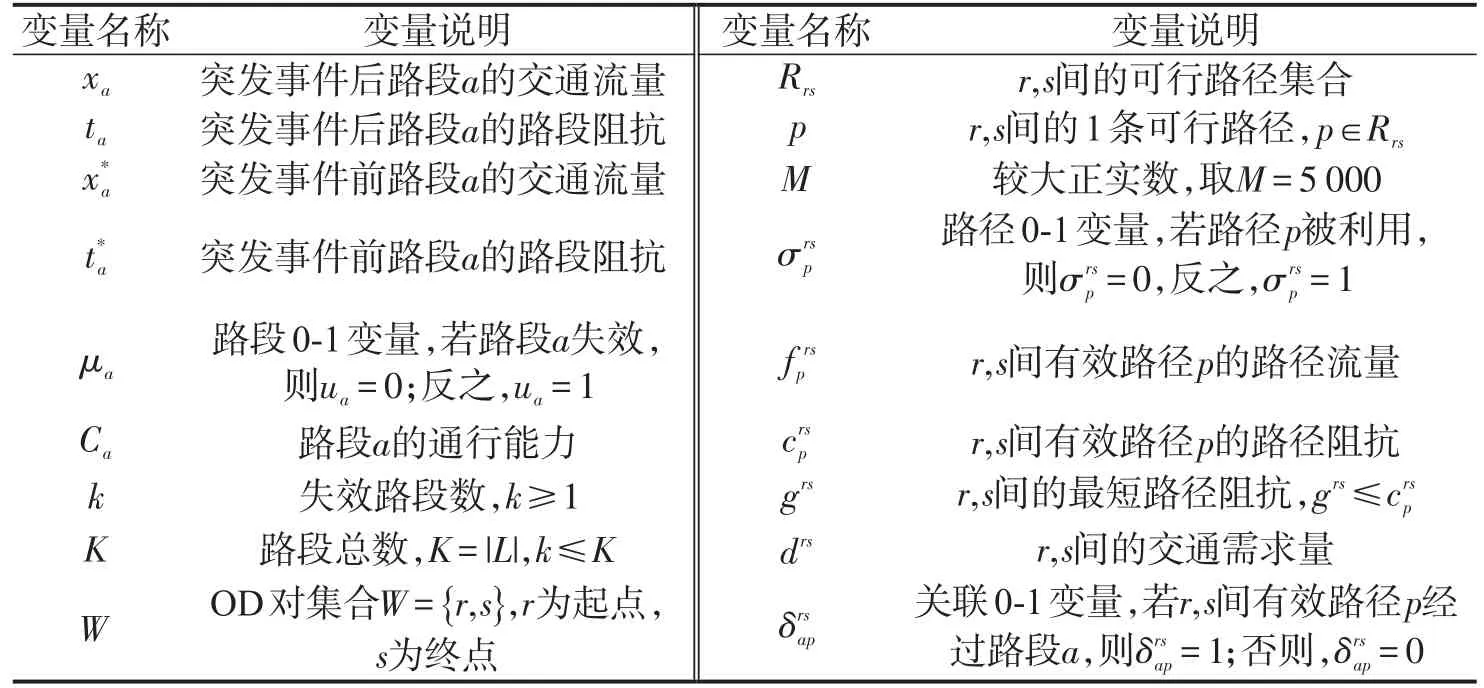
表1 模型的符号变量说明Table 1 Notation’s description in the model

2.2 目标函数

与传统方法[1-4,7-8]不同，本文构建的目标函数为“max型”，用于寻找使路网G(N,L)总阻抗变化最大的关键路段，对应的识别指标为

2.3 约束条件

模型的约束条件分为3类：路段通行能力约束、路径流量约束和路网均衡约束.引入相应的0-1变量进行描述.

(1)通行能力约束.

首先，利用路段0-1变量ua，ua∈{0,1}、路段a通行能力Ca、失效路段数k等来表征路段通行能力约束，即

式(4)实现了突发环境下路网从单条到多条路段失效的情景刻画；式(5)描述了路段通行能力限制.

(2)路径流量约束.

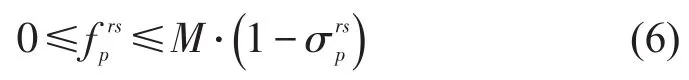
式(6)中，当路径p是均衡状态下的可行路径时，参数，从而保证了路径流量的非负性.

(3)路网均衡约束.

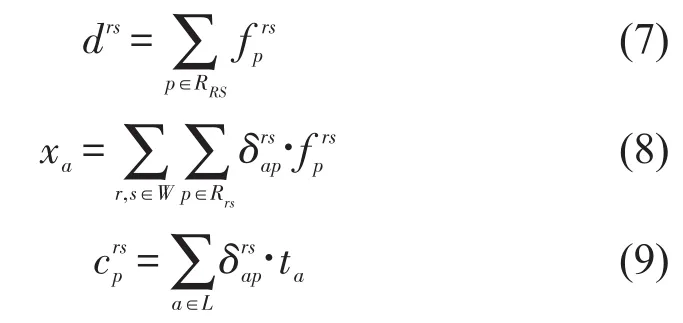
式(7)保证了路网需求均衡；式(8)刻画了路段交通流；式(9)描述了有效路径阻抗.

综上，该模型从路段、路径、路网等3个方面约束了突发环境下的网络流量平衡，是一个混合0-1非线性规划，求解算法较为复杂且不能保证获得可行解[5]，故需进行线性化处理.

2.4 线性化处理

不难发现：除了目标函数与约束条件的式(9)含有路段阻抗ta，需利用BPR函数计算，模型其余部分均为线性形式，故只对这两部分进行处理.

(1)目标函数线性化.

故，可在前文“路径流量约束”中增设表征Wardrop均衡原理的约束条件，即

实现原始目标函数从路段形式到路径形式的等价转换.转换后的目标函数为

其决策变量是grs(参数drs、均已知).它通过约束条件式(11)和参数紧密联系，而参数在“路网均衡约束”中由式(7)～式(9)量化.

(2)约束条件线性化.

路段阻抗ta一般按BPR函数计算[5]，即

式中：α为具体参数，本文取α=0.15.

显然，式(14)对于βa是线性的.下面，利用xa对βa进行“分段逼近”，如图2所示.

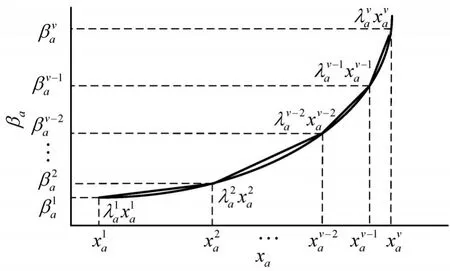
图2 βa的分段线性化逼近Fig.2 Piecewise linear approximation ofβa

图2中，v为区间数；为xa在对应区间的值.非线性函数被v个线性函数“逼近”.显然，当v越大，函数逼近的效果越理想.本文取v=50，将逼近方式表述为

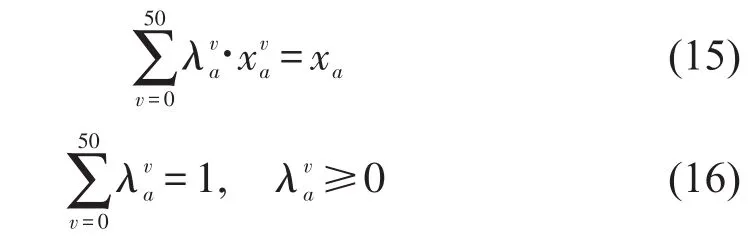
式(15)和式(16)用于确定区间划分方式；式(17)采用“层层递加”的方法“逼近”βa.

最后，得到模型的最终形式为

式(19)为通行能力约束；式(20)为路径流量约束；式(21)为路网均衡约束；式(22)为分段线性约束.目标函数和约束条件均是线性的，且含有ua、等3个0-1变量，是典型的混合0-1规划问题.

3 求解算法

利用分支定界法求解通过线性化处理的混合0-1规划问题.

Step 0初始化.对G(N,L)进行初始配流，得到正常情况下各路段的初始阻抗、初始交通量及分段线性因子

Step 1事故模拟.确定失效路段数k(k≤K)，从潜在关键路段集合L′中选择k个路段，将它们从G(N,L)删除，得到更新路网G′(N′,L-k).

Step 2标准化.依据G′(N′,L-k)将(P0)转变为“标准形式”，便于直接套用单纯形法求解，并置Z″初值为+∞.

Step 3分支.选择下标i∈NF，用单纯形法解松弛子问题，解为x()i，目标函数值为 fi；如果无解，则置fi=+∞.

Step 4若fi=+∞，则置NF=NF-{i}，转Step8；否则，执行Step5.

Step 5若fi≥Z″，则置NF=NF-{}i，转Step8；否则，执行Step6.

Step 6定界.若 fi＜Z″，且x()i∈S()P0，则置Z″=fi，xˉ=x()i，NF=NF-{}i，转 Step8；否则，执行Step7.

Step 7再分支.若 fi＜Z″，且，则将分解成2个子集，i1,i2∈NF，置转Step3.

Step 8若NF≠∅，则转Step3；否则，算法终止，xˉ为(P0)的最优解，Z″为目标函数值.

在最后的可行解中，通过观察参数ua中的零元素，即可找到对应的关键路段.至于关键路段的数目(零元素个数)则由失效路段数k决定.

4 算例分析

算例网络G(N,L)由4个OD对、21个节点和33条路段组成，如图3所示.路段具体参数如表2所示.网络上共 4 个 OD 对：(1,14)、(1,18)、(4,14)、(4,18).网络的各条路段均是双向的，限于论文篇幅，只列出了正向路段的基本参数并进行了鲁棒性分析与网络配流.

下面，分别进行路网特性分析与关键路段集识别：

(1)路网特性分析.

每次从G(N,L)中删除1条路段，运用Matlab2012a按式(1)和式(2)计算突发事件前后路网鲁棒性指标的变化量ΔE和ΔS，结果如图4所示.

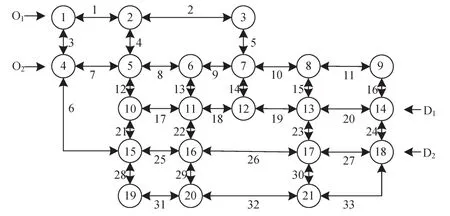
图3 算例网络Fig.3 Example network

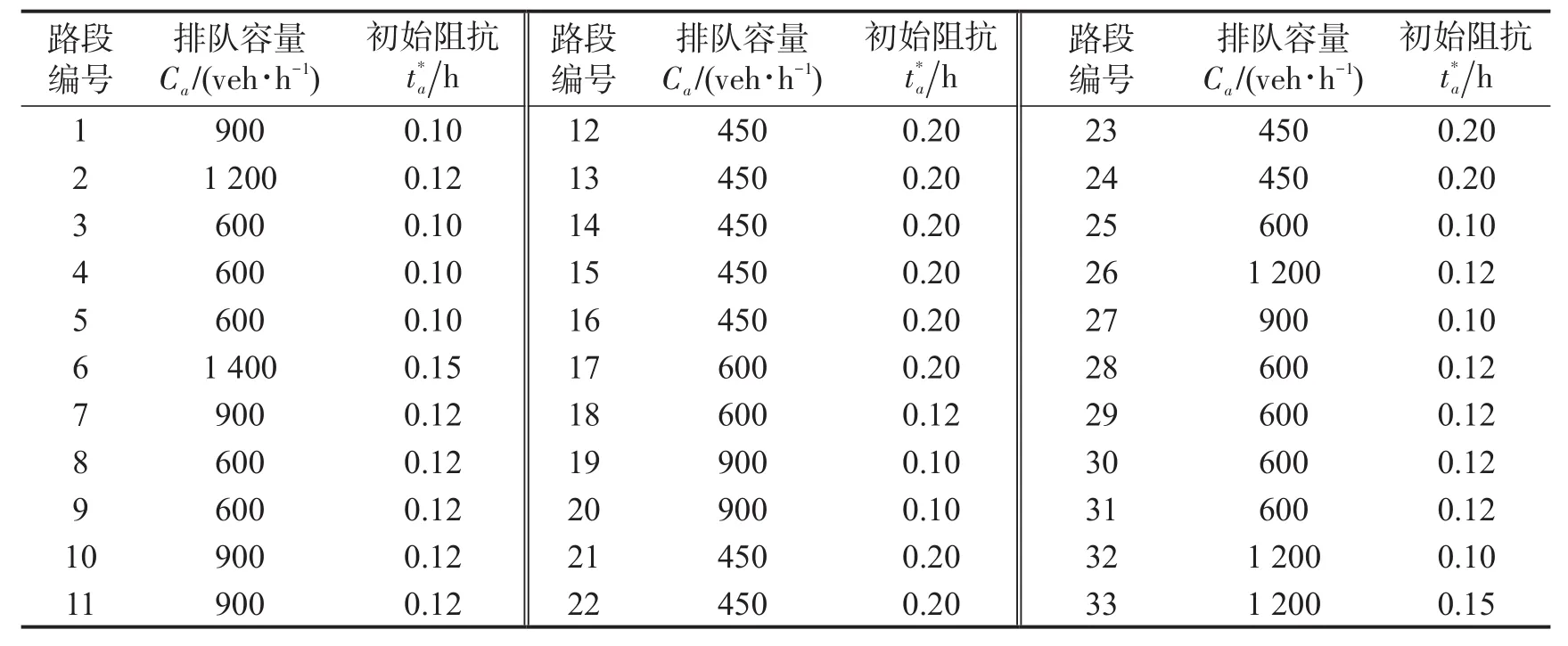
表2 路段基本参数(正向)Table 2 Links’basic parameters(Forward direction)

图4 突发环境下的路网鲁棒性指标变化Fig.4 Road network’s robustness index changes under emergency environment

将图 4中ΔE与ΔS的均值：，作为路网潜在关键路段的筛选条件，选择变化量均大于的路段构成潜在关键路段集合L′，即

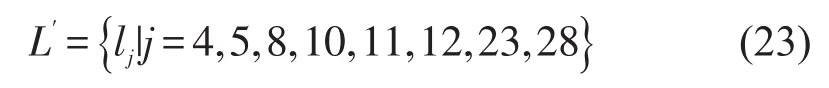
式中：j为路段编号.

(2)关键路段集识别.

设OD需求为

先从单条路段(k=1)失效入手，得到对应的关键路段识别指标(Z″-Z0)，结果如表3所示(以无通行能力约束的关键路段识别模型[1-4]作对比).

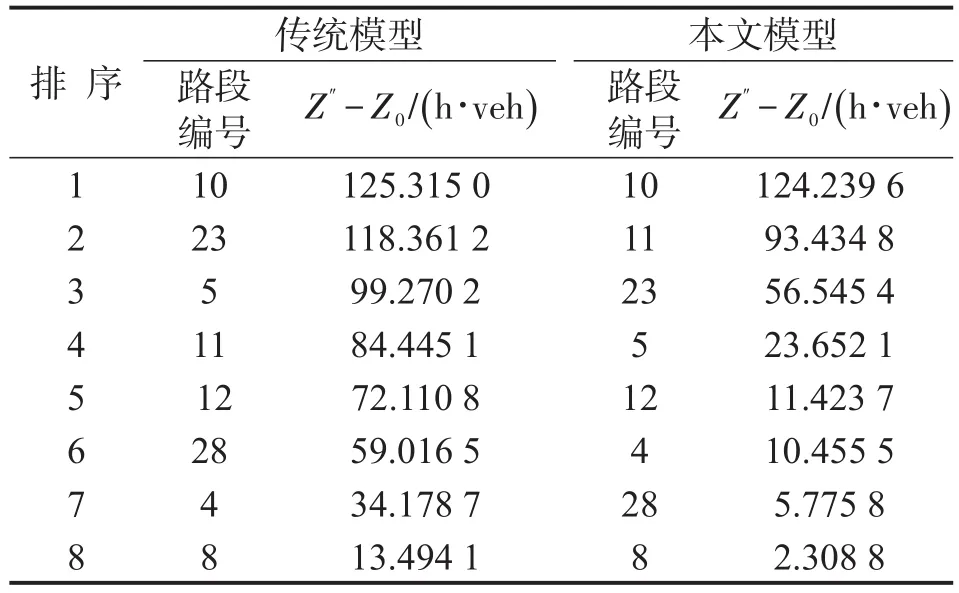
表3 识别结果对比(k=1)Table 3 Comparison of recognition results(k=1)

由表3可知，在k=1的情况下，网络能够满足相应的OD需求，且2种模型对关键路段的识别结果均为：路段5、路段10、路段11和路段23.

接着，将k:2→8逐一取值，进行多条路段失效(k＞1)的路网关键路段集识别，结果如表4所示.

由表4可知，对于多路段失效，2种模型的识别结果也基本相同.但传统模型耗时随着失效路段数的增多呈现“指数增长”，而本文模型耗时却“稳中有降”.原因在于：传统模型需要在备选集中进行一次排列组合操作，并遍历各种可能的关键路段组合，这导致计算复杂度显著增大；而本文模型以零元素个数表示关键路段数，计算难度会随着零元素个数的增加而平稳下降.

表4 多条路段失效下的路网关键路段集识别Table 4 Road network’s critical links set identification with multiple links failure

另外，对比多路段失效与单条路段失效的识别结果，有：①(4,5)、(4,5,10)、(4,5,10,12,28)等集合的路段在几何拓扑上没有邻接关系；②关键路段集并非表3中关键路段的简单集成，如表4关键路段集里的路段4、路段12、路段28等，在表3的排名均靠后.

为了解释上述现象，本文试对失效路段数与识别指标值间的关系进行描述：先绘制散点图，然后利用非线性插值拟合关系曲线，结果如图5所示.

由图5可知，曲线拟合度很高(97.77%)，且走势变化与文献[7]和[9]中路网鲁棒性分析结果是“逆向”的.这说明，突发环境下的路网鲁棒性与总阻抗变化量之间存在“逆向”曲线关系：即随着失效路段增多，路网将变得更为脆弱且渐趋其鲁棒性的极限.故可利用拟合曲线实现两者的相互转化.

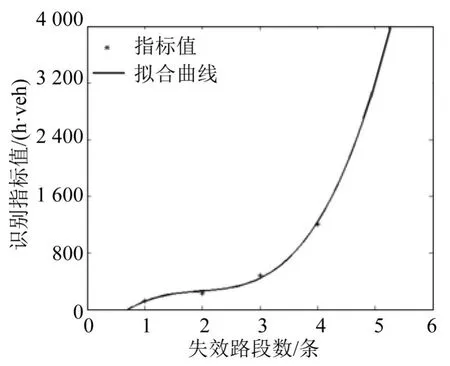
图5 失效路段数与指标值的关系Fig.5 Relationship between with the number of links failure and index values

5 结论

本文针对突发环境下的路网关键路段集识别，得到相关结论如下：

(1)考虑路段通行能力约束，可有效降低对关键路段的误判；

(2)关键路段集并非若干关键路段的集成，其构成元素一般无邻接关系；

(3)突发环境下的路网鲁棒性与总阻抗变化量间存在“逆向”曲线关系.

然而，如何在获得关键路段的基础上进行路网应急控制，则是未来的研究方向.

参考文献：

[1]BERDICA K.An introduction to road vulnerability:What has been done,is done and should be done[J].Transport Policy,2002,9(2):117-127.

[2]D'ESTE G M,TAYLOR M A P.Model network vulnerability at the level of the national strategic transport network[J].Journal of the Eastern Asia Society for Transportation Studies,2001,1(2):1-14.

[3]JENELIUS E,PETERSEN T,MATTSSON L G.Road network vulnerability:Identifying important links and exposed regions[J].Transportation Research A,2006,6(40):537-560.

[4]SULLIVAN J L,NOVAK D C,et al.Identifying critical road segments and measuring system-wide robustness in transportation networks with isolating links:A linkbased capacity-reduction approach[J].Transportation Research Part A,2010,44(95):323-336.

[5]WANG D Z W,LIU H,SZETO W Y.Identification of critical combination of vulnerable links in transportation networks:A global optimisation approach[J].Transportmetrica A:Transport Science,2016,12(4):346-364.

[6]FARAHANI R Z,MIANDOABCHI E,SZETO W Y,et al.A review of urban transportation network design problems[J].European Journal of Operational Research,2013,229(2):281-302.

[7]张玺.基于网络效率的日变路网脆弱性识别方法[J].交通运输系统工程与信息，2017,17(2):176-182.[ZHANG X.Day-to-day road network vulnerability identification based on network efficiency[J].Journal of Transportation Systems Engineering and Information Technology,2017,17(2):176-182.]

[8]李彦瑾,罗霞,车国鹏.突发拥挤条件下城市道路网脆弱性识别[J].公路交通科技,2017,34(5):129-136.[LI Y J，LUO X，CHE G P.Vulnerability identification of urban road network underabruptcongestion condition[J].Journal of Highway and Transportation Research and Development,2017,34(5):129-136.]

[9]ZHAO G F,YUAN S W,CI Y S.Analysis of complex network property and robustness of urban road network[J].Journal of Highway and Transportation Research and Development,2016,33(1):119-124.