参照系变换及其在物理解题中的应用研究

冉婷 兰小刚 余杰

摘 要：简要回顾经典力学与狭义相对论时空观，运动相对性原理的内涵，并对时间和空间的概念作简要描述。并通过实例，详细讨论了参照系变换思想在求解物理问题中的重要性。以期加深学生对物理学中时间和空间概念的理解，激发学生对物理学进行探索和研究的兴趣。

关键词：经典力学；狭义相对论；参照系变换

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2018）3-0058-3

1 引 言

研究物体运动规律是经典力学的主要研究目标之一，为了定量地描述物体的机械运动，我们需要选择适当的参照系。而力学概念，如速度、加速度等，以及力学规律都是对一定的参考系才有意义[1，2]。学生习惯于选取地面为参照系，不善于变换参照系，解决物理问题时常常陷入困境。本文首先简要回顾经典力学与狭义相对论时空观，运动相对性原理的内涵，对时间和空间的概念作简要描述。期望能够用简单易懂的语言，让学生正确理解“动”与“静”的辩证关系，加深对时间和空间概念的理解，提升学生对力学规律的认识。

2 经典力学时空观与狭义相对论时空观

自古以来，空间的概念来源于物体的广延性，时间的概念则来源于过程的持续性。早在1632年，伽利略曾在封闭的船舱里仔细观察了力学现象，发现在船舱中察觉不到物体的运动规律和地面上有任何不同[3]。由此，伽利略总结出力学的相对性原理，或伽利略相对性原理（Galilean principle of relativity）[4]： 在一个封闭的系统中，不论进行怎样的力学实验，都不能判断一个惯性系统是处于静止状态或是在做等速直线运动。在经典力学中，时间和空间都是绝对的，即：相对于不同的参照系，同样两点之间的距离或同样两个事件之间的量度与参考系无关，无论在哪一个参照系中测量，其结果都是一致的。牛顿曾说过“绝对的、真正的和数学的时间自己流逝着，并由于它的本性而均匀地与外界对象无关地流逝着，与任何外界事物无关。”在牛顿力学中，空间和时间的量度都是绝对的，二者不仅被看作同物质一样的独立存在，而且还扮演了某种有绝对意义的角色[5]。

在牛顿等对力学进行深入研究后，人们对光和电磁现象的研究也逐步深入，逐渐形成了比较严整的电磁理论——麦克斯韦理论[6]。伽利略变换能否用于麦克斯韦电磁理论引起了物理学家的广泛思考。在1887年，著名的迈克尔-莫雷实验证实：光或电磁波的运动不服从伽利略变换。爱因斯坦在1905年发表的《论动体的电动力学》论文中，提出著名的狭义相对论的相对性原理和光速不变原理，建立了一套完整的理论——狭义相对论，而把物理学推进到一个新的阶段[7]。狭义相对论否定了脱离物质运动的“绝对时间”和“绝对空间”的概念，指出时空与物质运动不可分割。

3 参照系变化与求解物理问题

所有的时空测量都是在某个参照系中或某个参照物上、通过使用某套时空测量标准而进行的，离开了参照物和时空测量标准，时空测量就无法进行。对中学生而言， 对时间和空间的认识深度有限，在分析物理问题或物理现象时，往往缺乏参照系变换的概念。实际上，在一个问题中若未指定参照系，则通过选定适当的参照系可使运动的描述得以简化，从而使问题的解决得以简化。在物理试题中有不少关于两物相距的问题。学生往往习惯于选取地面为参照系，来描述物體的运动。但在处理某一类问题中，采用这种常规解法，会使得求解过程繁琐， 若学会变换参照系来研究此类问题， 会大大简化解题过程。接下来我们将通过在两个简单的例子中，选取不同的参照系来研究物体的运动规律。

如图1所示，在同一竖直平面上沿两个相互垂直的方向以vA=10 m/s、vB=20 m/s的初速度抛出A、B两个小球。 问1 s后A、B相距多远？（假设A、B两球未着地，并忽略一切阻力）

在处理此类问题时，学生往往习惯于以地面为参照系。利用抛体运动规律，分别列出A、B两球的运动学方程。然后求得1 s后A、B两球的位置坐标。再利用两点间距公式，求出两球的距离。但我们也应该注意到，这种求解过程会涉及求解高次方程组，计算过程相当复杂。

但如果我们换一个参照系来研究二者的运动，即：选取一个初速度为零，加速度为g，在A、B两球被抛出时同时开始向下运动的参照系。在该参照系中观察，A、B两球相对对方以相互垂直的方向做匀速直线运动。显然，很容易求得在1 s后二者之间的距离为：

为了直观反映出通过不同参照系中观察到的运动规律，我们采用Matlab进行了部分数值模拟。如图2（a）中所示为在地面参照系中观察，选取发射角φ分别为π/6、π/4、π/3时，观察到A、B两个物体的斜抛运动轨迹。显然，直接求解二者之间的间距会非常困难。图2（b）通过Matlab模拟出在地面参照系中，观察到的A、B两球的间距与时间的变化规律：二者间距与时间成正比例关系。这与我们选取的在抛出A、B两球同时开始自由落体的参照系中观察到的结果完全一致：A、B两球相对对方以相互垂直的方向做匀速直线运动。此外，图2（b）是选取发射角φ分别为π/6、π/4、π/3时，A、B两球间距与时间变化的数值计算结果。可见，只要A、B两球速度不变，即使沿不同发射角φ发射，A、B两球的间距与时间变化体现出完全一致的正比例关系，与发射角φ无关，进一步验证了我们假设的正确性。

运动轨迹及二者间距随时间变化关系

在处理另一类斜抛问题时，也可以采纳类似的参照系变换方法，可以避免处理复杂的斜抛运动。如图3所示，用一只玩具手枪瞄准一小球开枪，子弹的发射速度v=12 m/s，假设小球离枪口的竖直高度H=7 m，水平距离L=11 m。在子弹发射同时，小球开始由初速度为零自由下落，忽略一切阻力。子弹能否击中小球？若能击中，需要多少时间？

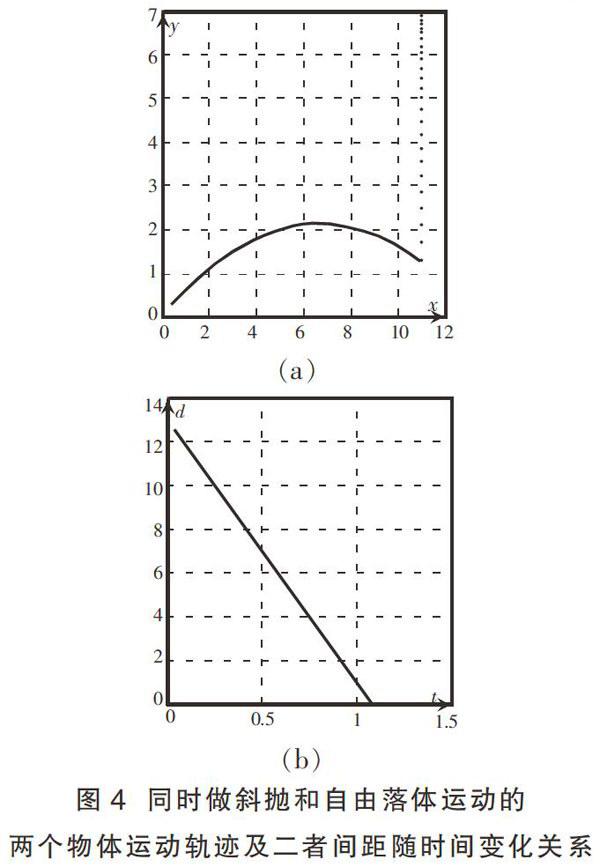
显然，如果选取地面为参照系，如图4（a）所示，将涉及到选取分析一个自由落体运动和斜抛运动，求解过程会非常复杂。但如果我们以自由下落的小球为参照系，我们将看到子弹将以速度v向小球匀速运动，子弹必将击中小球，且所需时间为：t=■/v=1.1 s（2）

在图4（b）中，我们通过Matlab进行了数值计算，作出了在地面参照系中观察子弹与小球间距随时间的变化关系。显然，二者间距随时间线性递减，证明我们假设的正确性，即：若以小球为参照系，将看到子弹以速度v做匀速运动。显然，我们仅仅通过一个参照系变换就使该求解过程大大简化，构建出相当简洁、直观的物理图像。

两个物体运动轨迹及二者间距随时间变化关系

4 结论与讨论

研究和描述物体运动，只有在选定参照系后才能进行。合理选择参照系，会使一个复杂的物理过程变得简单、明了[8]。本文列举了两个例子，详细讨论了参照系变换思想在求解物理问题中的重要性。我们撰写本文的目的不是为了讨论求解某些类型物理问题的方法和技术，而是想通过介绍经典力学中最基本的参照系变换思想，加深学生对物理学中时间和空间概念的理解，激发学生对物理学进行探索、研究的兴趣，并为以后进入更高层次的物理学学习奠定基础。

参考文献：

[1]张申如，孙松庚.作用力与反作用力做功之和与参照系无关的一种证明[J].大学物理，1986（1）：44.

[2]许洪林.非惯性参照系中机械能转换和守恒定律及功能原理的沿用[J].大学物理， 1984（2）：13-15.

[3]A.柯瓦雷，晓怡.伽利略与17世纪的科学革命[J].世界哲学，1994（4）： 55-61.

[4]朱惠萍.伽利略研究的历史线索[J].自然辩证法通讯，1990（6）：59-63.

[5]张元仲.从牛顿力学到狭义相对论[J].力学与实践，2005（4）：1-7.

[6]向义和.麦克斯韦电磁场理论的建立[J].物理，1991（1）：43-48.

[7]倪光炯，陈苏卿.关于狭义相对论的本质[J].复旦学报（自然科学版），1996（3）：325-334 .

[8]冉婷，余杰，兰小刚.惯性参考系的选择与机械能守恒[J].物理教学探讨，2017，35（9）：38-39.