加筋板穿透数值仿真中网格尺寸对失效应变的影响分析研究

谷家扬，凌 晨，邓炳林，王 璞，周 佳

（1.江苏科技大学 海洋装备研究院，江苏 镇江212003；2.中国船舶及海洋工程设计研究院，上海 200011）

0 引 言

碰撞事故是海洋结构物在营运过程中常见的海损事故之一，破坏性较大的碰撞事故一旦发生，将有可能直接带来经济损失，甚至会给生命财产和生态环境带来严重后果。因此，船舶与海洋结构物碰撞事故下的结构强度分析问题一直是国内外船舶结构力学界关注的热点之一，同时对此也开展了大量的试验研究工作[1-6]。

加筋板是组成海洋工程结构物的基本单元，发生碰撞事故时，加筋板的损伤变形是碰撞能量主要的吸收机制[7]。因此，研究加筋板结构在碰撞载荷作用下的动态响应问题对深入理解船舶碰撞的内部动力学问题和开展海洋工程结构物耐撞性结构设计都具有重要指导意义。随着非线性有限元分析（Non Linear Finite Element Analysis，NLFEA）技术和计算机硬件系统的发展，在分析碰撞事故下结构的动态响应时，越来越多的学者采用有限元法进行碰撞机理研究[8-12]，并从中得到了一些对碰撞事故分析方法、碰撞安全性评估及耐撞性结构设计等具有重要指导意义的结论。采用NLFEA技术，对于不同类型的碰撞问题，可以较为精确地描述船舶和被撞体两者复杂的几何形状、材料本构、破坏损伤等信息，从而能够得到更精确的结果，较传统的经验公式计算体现了较大的优势。

在船舶与海洋结构物碰撞事故这种典型的高能碰撞中，涉撞区构件往往会因延展性超过极限值而发生断裂失效现象。在运用NLFEA方法对高能碰撞过程模拟时，能否准确模拟材料的断裂失效现象，对于碰撞计算结果的准确性具有非常重要的意义。目前主流软件对碰撞过程的数值模拟，一般是通过定义材料模型的失效准则来表达结构的断裂失效现象，该现象的直接体现便是失效单元不再具有承载力。因此，材料断裂失效应变取值在有限元仿真软件里是一个非常重要的参数，它直接控制钢材断裂失效的模拟，同时对结构体现出的力学性能的数值仿真也具有很大的影响。

工程上应用最广泛的断裂失效准则是最大等效塑性应变失效准则，大多数非线性有限元软件也都采用此准则。该准则所确定的失效应变取值与有限元模型所采取的网格尺寸具有明显的依赖关系，因此网格尺寸与失效应变取值的确定对仿真结果的可靠性与准确性具有重要意义。国内外研究人员针对失效应变与网格尺寸之间的关系也做了相应的研究工作[4-6，13-14]，给出了网格尺寸与失效应变取值的关系曲线，研究表明：网格划分得越精细，其失效应变取值就越大。然而，大部分现有网格尺寸与失效应变取值的关系曲线都是基于光板冲击或杆件的拉伸试验并与有限元仿真结果进行拟合来确定的。对于加筋板结构，碰撞仿真模拟时其失效应变取值是否可以直接从基于光板穿透试验所确定的关系曲线中加以确定是一个值得讨论的问题。

实际碰撞事故过程中，加筋板架直接承受撞击体的面外碰撞载荷而产生穿透失效，因此在做碰撞事故下板架失效机理分析时一般可从板架的穿透试验进行研究。本文首先对Alsos[2]所做的光板、加筋板准静态穿透试验进行简要介绍，参照其试验结果，采用非线性有限元仿真软件LS-DYNA对光板及加筋板进行穿透仿真分析。通过改变不同网格尺寸下的失效应变取值来拟合试验结果，进而探讨光板与加筋板在碰撞仿真分析中网格尺寸与失效应变取值之间的关系，同时还对加筋板结构碰撞仿真模型是否考虑焊缝进行了讨论，得到了对具有加筋板结构进行碰撞有限元仿真分析时确定失效应变取值的规律，这对于今后碰撞仿真分析具有一定指导意义。

1 Hagbart S.Alsos的光板与加筋板准静态穿透试验

1.1 试验设置及试验模型

模型试验设置如图1所示，模型的冲击破坏通过最大压力达到250 t的液压千斤顶以10 mm/min恒定速度准静态加载来完成。撞头顶点与试验模型的中心重合，碰撞力和撞头的位移通过液压千斤顶上面的传感器进行测量。为了准确评估试验模型发生失效破坏的位置，对试验模型板壳进行绘制网格线，试验时对试验模型两横向端部及底部进行约束。受液压千斤顶位移量程（150 mm）的限制，试验过程中首先将外载增加到135 mm左右，随后将外载卸载，接着继续缓慢加载，直到试验模型发生失效破坏为止。

图1 试验设置[2]Fig.1 Experimental set-up[2]

1.2 试验模型

Alsos对一个光板模型及4种加筋板模型进行了系列准静态穿透试验，这里选取光板（US）模型与设置有两道扁钢骨材（2 Flat Bar）的加筋板（2FB）模型进行介绍，模型试件如图2所示。矩形板壳的几何尺寸为1 200 mm×720 mm，板厚为5 mm；两加强筋均为扁钢，间距为240 mm，截面尺寸均为120 mm×6 mm；矩形板壳四周与结构较强的钢箱焊接在一起，钢箱截面尺寸为300 mm×200 mm，厚度为12.5 mm。撞头为一个带有球头刚度较大的实心锥形体，锥形体扩张角为90°，球头半径为200 mm，如图2所示。加强筋通过焊接方式与矩形板壳连为一体，加强筋端部固定在钢箱上，各构件的装配均依照船厂的加工要求来完成，各构件材料参数如表1所示。

表1 各构件幂指数塑性材料参数[3]Tab.1 Power law material parameters for the various components[3]

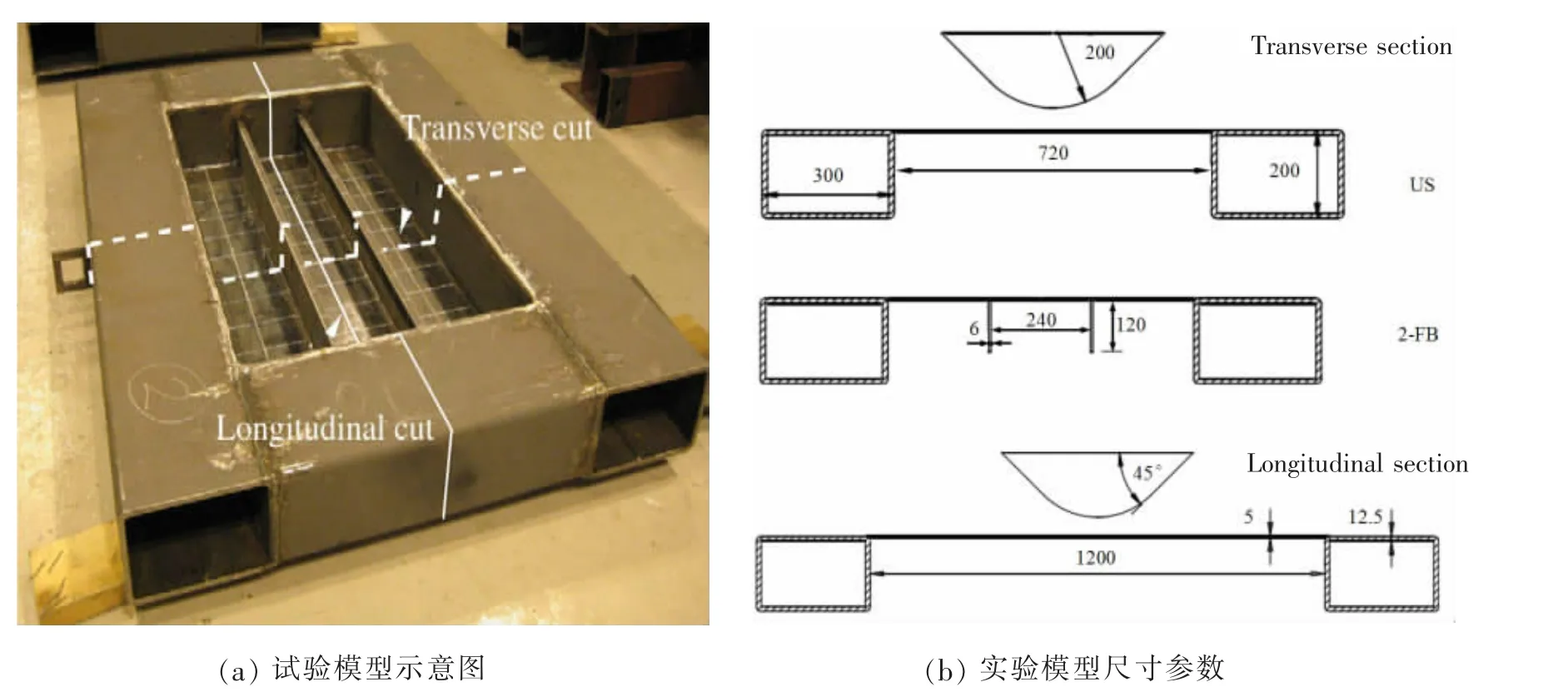
图2 光板(US)及加筋板(2FB)试验模型[2]Fig.2 Test model of none stiffener of plate(US)and two flat bar in plate(2FB)[2]

2 光板与加筋板准静态碰撞仿真模拟

采用Hypermesh/LS-DYNA分别对光板和加筋板建立有限元模型，分别构建5、10、15、20、25、30及40 mm等7种网格尺寸模型进行系列碰撞仿真模拟，每一种网格尺寸模型均采用单元厚度方向定义5个积分点的Belytschko-Lin-Tsay壳单元，图3所示为10 mm单元网格的有限元模型。各构件幂指数塑性材料参数按表1进行确定，对应LS-DYNA中MAT.18号材料。由于模拟的是准静态穿透过程，不考虑材料应变率效应，因此为加快计算效率，数值仿真时取撞头恒定加载速度为10 mm/s，即为试验加载速度的60倍。撞头假定为刚体，撞头顶点位于矩形平板中心以上5 mm高度处，撞头与矩形平板之间的摩擦系数取为0.3，对光板及加筋板定义结构失效时采用最大等效塑性应变失效准则。

图3 光板（US）及加筋板（2FB）有限元模型Fig.3 The finite element model of US and 2FB

对于加筋板，由于扁钢骨材与矩形板壳焊缝的存在会造成板壳与扁钢骨材交汇处局部厚度的变化，从而造成板壳断裂模式的改变[15]。当采用小网格尺寸建模时，有必要考虑焊缝的存在，可将焊缝以增大局部板壳和加强筋厚度的形式进行等效处理，具体而言，是在壳板焊接处各边宽约为3.5 mm区域增厚2 mm，加强筋焊接处高约为5 mm区域增厚4 mm[3]，如图4所示。然而采用较大网格建模时，焊缝属于小特征结构，是否有必要考虑焊缝的存在还需要探讨。

在各组碰撞仿真分析中，以试验结果为参考，对于确定的网格尺寸模型，通过搜索不同的失效应变值，得到不同的碰撞力-撞深曲线，使试验与数值仿真的碰撞力-撞深曲线基本一致，同时定义数值仿真计算得到的板壳断裂失效时临界撞深、临界吸能及碰撞力峰值与相应试验值的相对误差均在10%以下为最终搜索的失效应变值，相对误差定义如下：

图4 有限元模型中骨材与板壳交汇点“焊缝单元”截面图[3]Fig.4 Cross section illustration of‘weld element’ in the stiffener-plate junction in FEM[3]

板壳断裂失效时碰撞力峰值、临界撞深及临界吸能的试验结果如表2所示。

表2 光板与加筋板板壳断裂失效时的试验结果[2]Tab.2 Test results of plate and stiffened plate at the onset of fracture[2]

3 光板与加筋板碰撞仿真结果分析

表3-5给出了光板（US）、考虑焊缝加筋板（2FB）及忽略焊缝加筋板（2FB-NW）最终确定的失效应变值，由表中可知各参数相对误差均在10%以下，满足数值仿真与试验结果容许相对误差的精度要求。

表3 光板（US）板壳断裂失效时数值仿真结果Tab.3 Numerical simulation results of US at the point of fracture

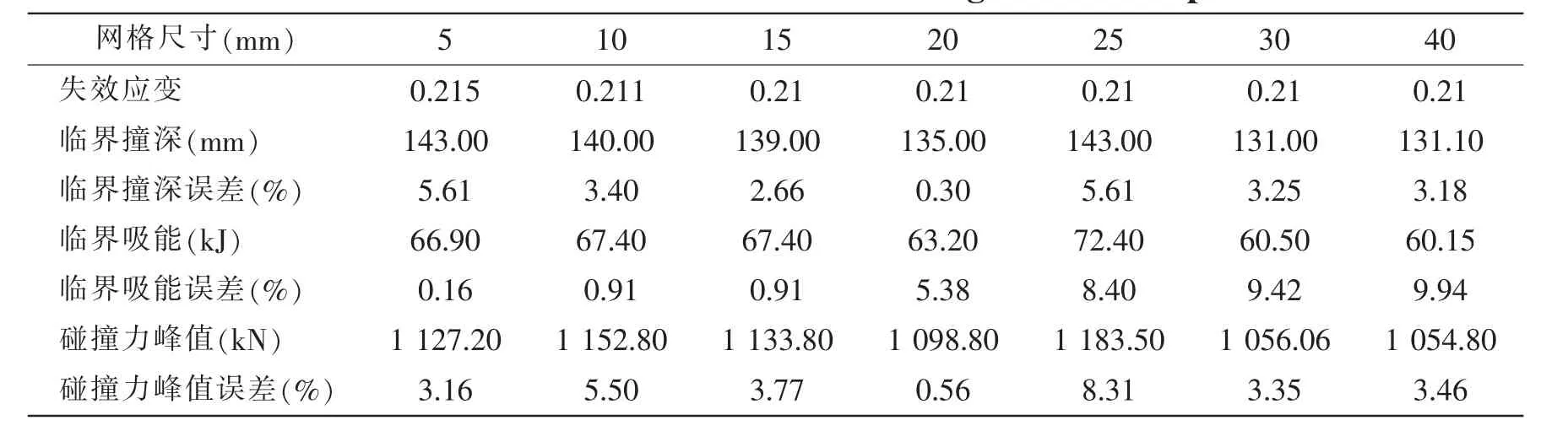
表4 考虑焊缝加筋板（2FB）板壳断裂失效时数值仿真与试验结果误差对比Tab.4 Numerical simulation results of 2FB considering weld at the point of fracture

表5 忽略加筋板（2FB-NW）板壳断裂失效时数值仿真与试验结果误差对比Tab.5 Numerical simulation results of 2FB ignoring weld at the point of fracture

从能量的角度来看，碰撞就是能量转换的过程，结构的塑性应变吸能在一定程度上可以表征结构的耐撞性能，而结构的吸能大小可以根据碰撞力-撞深曲线进行积分求得。因此，衡量数值仿真结果与试验结果的误差值，主要取决于临界吸能计算结果的准确程度，图5为根据表3-5中绘制的网格尺寸与临界吸能相对误差的关系曲线。

图 6给出了光板（US）、考虑焊缝加筋板（2FB）及忽略焊缝加筋板（2FB-NW）不同网格尺寸对应的碰撞仿真得到的碰撞力-撞深曲线，图中也给出了相应的试验曲线。从图6可以看出试验与数值仿真在碰撞力从0增大到峰值区间的碰撞力-撞深曲线基本一致，说明本文所采用的数值仿真方法及最终搜索确定的失效应变值可以很好地仿真再现准静态碰撞冲击动力学过程，结合表3-5可知，该仿真过程具有较高的精度。

图 7给出了光板（US）、考虑焊缝加筋板（2FB）及忽略焊缝加筋板（2FB-NW）网格尺寸均为5 mm的应变云图。从图7可以看出，对于相同的撞头及撞击速度，光板的耐撞性能明显优于加筋板。具体而言，光板发生失效时，临界撞深达到195 mm，临界吸能达到124 kJ，而加筋板撞深仅在142 mm或143 mm就发生断裂失效，失效位置出现在扁钢附近，此时临界吸能仅为67 kJ左右。

图5 网格尺寸与临界吸能相对误差的关系Fig.5 The relationship between the mesh size and the relative error of fracture energy

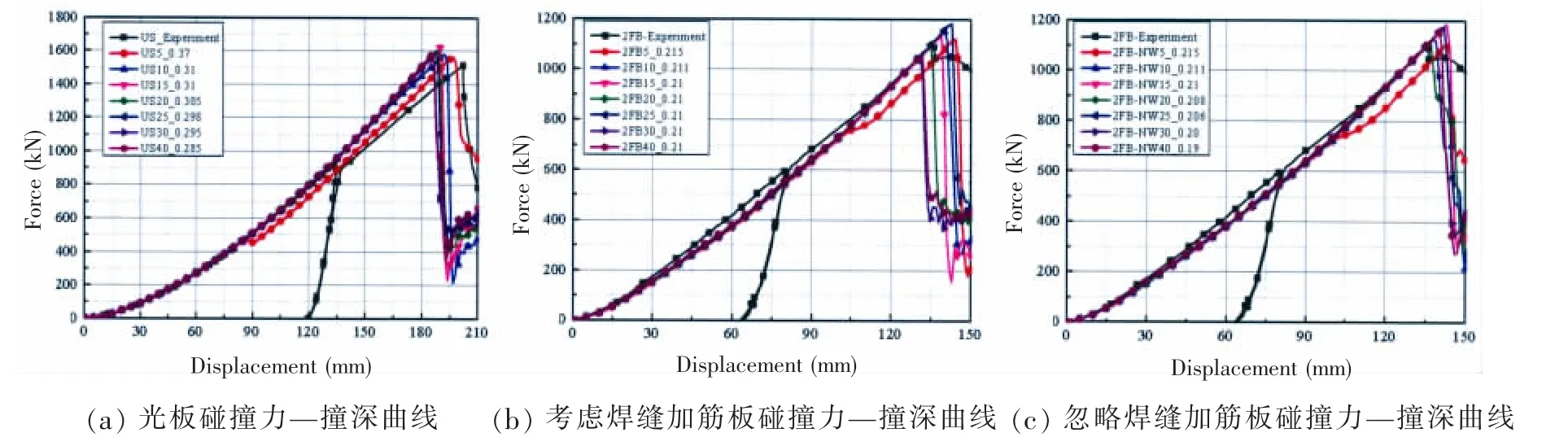
图6 碰撞力—撞深曲线Fig.6 Force-indentation curve

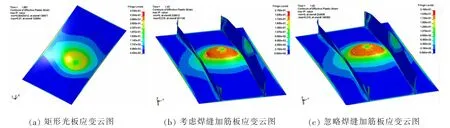
图7 三种有限元模型的应变云图Fig.7 Strain distribution for three different finite element models

由图7中光板与加筋板应变云图，还可以发现，光板在发生断裂失效时，较大应变云图覆盖区域相对较大，说明光板的塑性变形发展得更充分，即产生了更多塑性吸能从而吸收了更多的冲击能量。而对于加筋板，虽然扁钢的存在增大了整体板架的刚度，但却限制了矩形板壳产生塑性变形的范围，使板壳发生的塑性变形更加集中从而降低了板壳塑性吸能的能力，因此造成加筋板提前发生断裂失效。

对比图7（b）和（c）的应变云图可知，两者的应变云图基本一致，首次发生断裂失效的位置均发生在扁钢附近，扁钢的损伤变形模式均以膜拉伸、翘曲、扭转及折边为主。结合表4和表5可知，两者体现出的抗撞性能有所差异，考虑焊缝的临界撞深为143 mm，忽略焊缝的临界撞深为142 mm，由图5对比两者临界吸能的相对误差，可以发现考虑焊缝的计算结果更接近试验结果。

4 光板及加筋板有限元模型网格尺寸与失效应变关系

图8 有限元模型网格尺寸与失效应变取值关系曲线Fig.8 The relationship curve of element size and equivalent plastic failure strain

由碰撞仿真分析与实验结果对比，最终搜索得到满足精度要求的失效应变值。图8给出了光板（US）、考虑焊缝加筋板（2FB）及忽略焊缝加筋板（2FB-NW）不同网格尺寸对应的等效失效应变取值关系曲线。

从图8可以看出，对于同一种有限元模型，失效应变取值基本上都是随着网格尺寸的增大而减小，换言之，网格尺寸越精细，失效应变值就越大，结合图5可知，三种有限元模型所计算的临界吸能相对误差均随着网格尺寸的增大而增大，说明网格越精细，碰撞仿真所捕捉的应变能也越接近真实值；而相同网格尺寸下，加筋板的失效应变值要小于光板，且对比明显。这说明对于那些基于光板冲击或杆件的拉伸试验并与有限元仿真结果进行拟合确定的网格尺寸与失效应变取值关系曲线并不适用于加筋板结构，需要区别对待。同时也说明，对含有大量加筋板结构这类大型海洋工程结构物做非线性冲击动态数值仿真确定其材料失效应变取值时，应优先参考通过加筋板碰撞试验得到的网格尺寸与失效应变取值的关系曲线。

对比考虑焊缝加筋板与忽略焊缝加筋板模型的网格尺寸与失效应变取值关系曲线可以发现，考虑焊缝加筋板模型在网格尺寸大于15 mm以上时，失效应变取值恒定在0.21，表明焊缝存在较大网格的有限元模型是会影响板壳整体失效机制的，而忽略焊缝加筋板模型的关系曲线，则呈现随网格尺寸增大，失效应变取值递减的规律。

结合图5两者网格尺寸与临界吸能相对误差的关系曲线可知，网格尺寸小于20 mm以下时，考虑焊缝的有限元模型所计算的临界吸能相对忽略焊缝存在的模型要准确，然而当网格尺寸大于20 mm时即板壳厚度的5倍以上(网格尺寸约为最小焊缝单元的6倍以上)，考虑焊缝有限元模型所计算临界吸能的相对误差反而较大，说明在决定是否需要将焊缝予以在有限元模型中体现，要结合网格尺寸与焊缝覆盖区域进行对比来决定。此外，对于较大网格模型，焊缝相对于平均网格尺寸属于小特征结构，若仍考虑这类小特征结构，则需要花费较大的建模及计算成本，且计算准确度并没有提高，因此对于采用较大网格的分析模型并没有必要以等效单元形式来考虑焊缝。

5 结 论

本文基于Alsos所做的光板、加筋板准静态穿透试验结果，应用LS-DYNA软件对光板、考虑焊缝的加筋板及忽略焊缝的加筋板分别进行7种网格尺寸有限元建模并进行准静态碰撞仿真分析，通过对比分析得出以下结论：

（1）相同结构模型，网格尺寸越精细，等效失效应变取值就越大，碰撞仿真所捕捉的应变能也越接近试验观测值，但相应的建模及计算成本也会增加。

（2）相同网格尺寸的模型及相同的碰撞参数，加筋板与光板的失效应变取值存在明显的差异。因此，对含有大量加筋板结构的海洋工程结构物做非线性冲击动态数值仿真确定其材料失效应变取值时，应优先参考根据加筋板碰撞试验得到的网格尺寸与失效应变取值的关系曲线。

（3）以临界撞深及临界吸能的角度来看，相同碰撞参数下加筋板的耐撞性能相比光板的要差。这是因为：对于加筋板，由于扁钢的存在使板壳发生的塑性变形更加集中而降低了板壳塑性吸能的能力，因此造成加筋板提前发生断裂失效；而光板在发生断裂失效之前，可充分发挥光板的塑性变形能力，从而提高了自身的耐撞性能。

（4）加筋板结构中骨材与板壳之间的焊缝是否需要考虑，要结合网格尺寸与焊缝等效单元的相对大小进行决定。当网格尺寸不大于焊缝等效单元的5倍时，建议将焊缝以等效单元形式处理；而当网格尺寸为焊缝等效单元尺寸的5倍以上时，焊缝相对于平均网格尺寸属于小特征结构则没有必要将焊缝以等效单元形式在有限元模型中进行处理。

参 考 文献：

[1]Janssen M M H H,Schipperen J H A,Vredeveldt A W.Crashworthiness through smart use of high failure strain steel[J].Structures Under Shock&Impact XII,2012：345-356.

[2]Alsos H S,Amdahl J.On the resistance to penetration of stiffened plates,Part I-Experiments[J].International Journal of Impact Engineering,2009,36(6)：799-807.

[3]Alsos H S,Amdahl J,Hopperstad O S.On the resistance to penetration of stiffened plates,Part II：Numerical analysis[J].International Journal of Impact Engineering,2009,36(7)：875-887.

[4]Kitamura O.Comparative study on collision resistance of side structure[J].Marine Technology and SNAME News,1997,34(4)：293.

[5]Lehmann E,Peschmann J.Energy absorption by the steel structure of ships in the event of collisions[J].Marine Structures,2002,15(4-5)：429-441.

[6]Liu K,Wang Z,Tang W,et al.Experimental and numerical analysis of laterally impacted stiffened plates considering the effect of strain rate[J].Ocean Engineering,2015,99：44-54.

[7]刘 峰,王自力.加筋板抗撞击性能的比较研究[J].中外船舶科技,2006,3：1-2.Liu Feng,Wang Zili.Comparative study on impact resistance of stiffened panels[J].Shipbuilding Science and Technology,2006,3：1-2.

[8]胡志强,崔维成,杨建民.基于模型试验和数值模拟方法的深吃水立柱式平台碰撞特性[J].上海交通大学学报,2008,42(6)：939-944.Hu Zhiqiang,Cui Weicheng,Yang Jianming.Research on the collision characters of spar platform based on model test and numerical simulation methods[J].Journal of Shanghai Jiao Tong University,2008,42(6)：939-944.

[9]Haris S,Amdahl J.Analysis of ship-ship collision damage accounting for bow and side deformation interaction[J].Marine Structures,2013,32(7)：18-48.

[10]张相闻,杨德庆,胡志强.船舶碰撞事故数值模拟与评估通用流程[J].中国造船,2016,57(2)：120-128.Zhang Xiangwen,Yang Deqing,Hu Zhiqiang.A general procedure of numerical simulation and evaluation of ship collision accident[J].Shipbuilding of China,2016,57(2)：120-128.

[11]Drücker S,Steglich D,Merckelbach L,et al.Finite element damage analysis of an underwater glider-ship collision[J].Journal of Marine Science&Technology,2016,21(2)：261-270.

[12]林 明,吴胜军,侯学杰,等.港珠澳大桥FRP桥梁防撞护舷船碰撞数值模拟及结构设计[J].玻璃钢/复合材料,2016(7)：42-47.Lin Ming,Wu Shengjun,Hou Xuejie,et al.Numerical simulation of ship collision and structural design on FRP anti-collision fender of Hong Kong-Zhuhai-Marco bridge[J].Fiber Reinforced Plastic/Composites,2016(7)：42-47.

[13]Jeom K P,Pedersen P T.Modelling of the internal mechanics in ship collisions[J].Ocean Engineering,1996,23(2)：107-142.

[14]Kõrgesaar M,Ehlers S.An assessment procedure of the crashworthiness of an LNG tanker side structure[J].Ship Technology Research,2010,57(2)：108-119.

[15]Wang T,Hopperstad O S,Lademo O G,et al.Finite element analysis of welded beam-to-column joints in aluminium alloy EN AW 6082 T6[J].Finite Elements in Analysis&Design,2007,44(1)：1-16.