基于损伤力学和XFEM的舰船蒸汽轮机叶片裂纹扩展研究
2018-04-25李亚政孙亚非张广辉黄洪雁刘占生
李亚政,王 峥,孙亚非,张广辉,黄洪雁,刘占生
(1.哈尔滨工业大学 能源科学与工程学院,哈尔滨 150001;2.上海空间推进研究所,上海 200433)
0 引 言
叶片作为船用汽轮机的核心部件,其疲劳寿命的长短直接影响整个舰船动力装置的稳定可靠运行;若能在复杂工作环境中大致预测叶片的疲劳寿命,并在危险点出现前及时检修,将能在很大程度上减少事故的发生。目前,传统疲劳寿命分析方法[1]在计算疲劳寿命的过程中大多要根据实际经验进行修正,难以给出详细的裂纹具体扩展过程和具体发生破坏的循环次数,而连续介质损伤力学则能够较好地解决这一问题。
损伤力学是研究材料在各种不同的加载条件下,其损伤的演化发展直至破坏的过程。材料疲劳破坏的实质是材料在循环应力下的性能发生恶化而不断减损,其间断裂面的有效接触面积逐渐减小,材料的弹性模量等参数减小,间接造成应力、应变增大。目前损伤力学的基本理论已经越来越多地应用于材料的疲劳寿命评估。陈沙古等人[3]结合低周疲劳试验数据,在简化的椭圆形裂纹形状扩展模型的基础上提出了一种基于损伤演化的疲劳裂纹扩展寿命简化计算方法。张鼎等[4]将风暴模型和裂纹扩展率单一曲线模型及焊趾表面裂纹应力强度因子的计算方法结合起来,探讨了复杂载荷作用下船舶结构疲劳裂纹扩展预报方法。
本文基于损伤力学的基本理论,推导叶片低周疲劳的寿命模型,同时利用扩展有限元方法进行叶片裂纹扩展模拟和低周疲劳寿命分析,对比理论计算和数值模拟的结果,验证所提出的寿命模型的准确性。
1 循环载荷下的损伤力学模型
1.1 损伤数学模型
Lemaitre[5]文中提出的耗散能理论认为:疲劳损伤过程往往伴随着能量的流动以及损失,其间发生的材料性能劣化以及塑性应变均为不可逆过程,所以损伤的实质是不可逆的能量耗散过程,可以用耗散势函数将其表示出来,最终求得可以表达疲劳损伤过程的损伤本构方程。
在损伤演化的过程中,起主要作用的有以下几个状态变量,温度、应力、弹性应变、塑性应变、总应变、累积塑性应变以及损伤变量等。假设材料存在Helmholtz自由能ψ,且由于损伤与塑性不耦合,则其表达式为:

其中:ε为总应变;εe为弹性应变;εp为塑性应变;γ表示累积塑性应变;α为背应变;D为损伤变量。类比断裂力学中的能量释放率,定义损伤变量的伴随变量应变能释放率,其表达式为:
其中:σeq为Mises等效应力,Rv为三轴应力比,表达式为:

1.2 损伤演化方程及其修正
对于一个稳定的循环过程,考虑在材料受损的过程中损伤变量的变化,在此式中引入损伤变量D,其中塑性应变的微分表达式为:

选取损伤的增量形式进行推导。对于单次循环而言,塑性累积增量越大,表示材料受损的程度越高。损伤增量与应变能释放率Y成正比。损伤增量D˙表示为:

Lemaitre在推导损伤演化方程时,没有考虑材料在发生断裂时弹性模量的变化。而现今大量实验数据表明,钢材料在进入塑性区时弹性模量会下降6%-10%左右,所以将弹性模量用=E·(1- )D代替。将(2)式与(4)式代入(5)式,同时得到塑性应变增量的表达式:损伤增量定义为单次循环加载内损伤的增加量,则将上式写成微分形式为:

对于单次循环内的损伤,在积分式要考虑加载(0-1积分)和卸载(1-0积分)的过程[6],因此积分(6)式得:

(7)式中应力部分是针对于对称循环而言,对于非对称循环,在求解等效应力时考虑平均应力的影响,在(7)式中引入平均应力项加以修正,得到下式:

根据(8)式可以快速地计算出单次循环内损伤的增量。随着循环次数的不断增加,损伤变量D不断变大,危险部位的应力值不断增大,所以单次循环内损伤变化量也逐渐增大。与Morrow疲劳寿命公式不同的是,Morrow公式只能粗略估计材料总的疲劳寿命,而损伤变量的计算公式则体现出真实的材料失效过程,即损伤不是随着循环呈线性变化,而是呈类似指数增长的趋势。
在得到单次循环内损伤增量后,对损伤变量从0到1积分,即可得到低周疲劳寿命的表达式:

对于同一种材料,循环应变硬化系数n′、循环强度系数K′、杨氏模量等不随着构件形状、载荷大小而变化,而不同载荷直接影响的是应力幅值σeq以及材料常数S。
为了得到损伤随循环次数的变化过程,在积分的过程中,从0到D积分,可导出D的表达式为:

(9)(10)ND。过低周疲劳试验确定材料的低周循环疲劳寿命,再基于损伤力学的基本公式进行反推[5],即可得到材料常数S,在无法满足实验条件的情况下也可以通过(6)式曲线的斜率来确定等。在已知各项材料参数时,可以通过有限元分析,得到裂纹位置的应力状态,即可得到计算材料的低周疲劳寿命。
上述的低周疲劳寿命公式是在损伤变量由0到1积分得到的,即包括疲劳裂纹萌生以及疲劳裂纹扩展的寿命,但在试件的实际工作中,尤其是汽轮机的叶片,在非外物损伤的情况下,损伤变量达到1即完全断裂开是非常危险的,所以应该在适当的损伤情况下及时更换受损叶片。大量的试验表征,材料的疲劳裂纹扩展的寿命仅仅占总寿命的20%左右,损伤力学中将疲劳裂纹萌生和裂纹扩展的界限处的损伤变量值Dc称为损伤门槛临界值,加载过程中当损伤变量达到Dc时,一般可以认为材料发生破坏。本文叶片的材料为2Cr13,刘晓燕等通过疲劳试验测得其损伤门槛值约为0.094[7]。
2 基于损伤力学的裂纹扩展模拟
2.1 扩展有限元方法
裂纹位置处的应变不连续、几何界面处的位移不连续性和裂纹尖端的奇异性使得疲劳裂纹成为典型的不连续问题。求解不连续问题最有效的数值方法就是扩展有限元方法(XFEM),其适用于任意边界条件、几何形状和几何非线性问题等,因而成为分析裂纹等不连续问题的主要手段。XFEM所使用的网格与结构内部的几何或物理界面无关,克服了在裂纹尖端等高应力和变形集中区进行细密的网格划分所带来的困难,同时在模拟裂纹扩展时也无需对网格进行重新划分。
XFEM方法通过对已被裂纹分割开的单元和裂纹尖端所处的单元上的节点位移函数引入富集项加以表征,其表达式为[8]:

式中:第一项代表未受裂纹影响的单元的位移形函数,其中I是网格单元中所有的离散点集,N(x)表示传统有限元单元内的形函数, {u0I,v0I}T表示未被分割开的位移函数;第二项代表被裂纹完全穿透的单元的位移形函数,J是该区域内的节点集,如图1中空心节点位置,{a1j,a2j}T为裂纹位置单元修正后的节点自由度;H(x)为单位阶跃函数,模拟穿过裂纹面的位移跳跃,其表达式为:

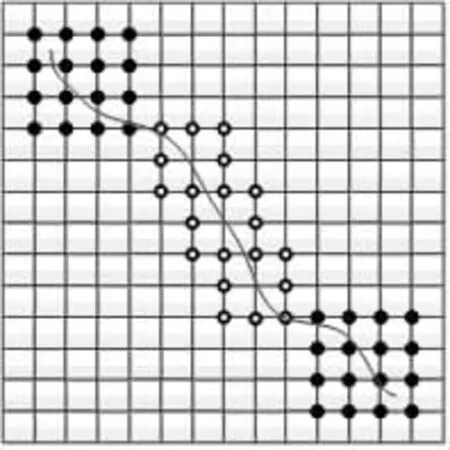
图1 裂纹及裂纹尖端单元节点图Fig.1 Crack and crack tip unit node map
完整的XFEM方程如下:

式中:Kuq、Muq是刚度矩阵中两种自由度的耦合项,F、V是与两种节点自由度对应的合外力,从方程中可见,在XFEM方法计算中,最重要的是计算出两种节点自由度。
2.2 ABAQUS低周疲劳分析技术
ABAQUS在低周疲劳分析方面有独特之处,它通过Direct cyclic分析直接计算结构稳态的循环响应,利用傅里叶级数及材料非线性行为的时间积分获得稳定的循环求解。该方法的基础是构造一个位移函数描述结构在整个循环载荷周期内所有时间点的响应。低周疲劳分析基础是损伤起始标准的判断。当循环中的结构响应稳定时,使用每个循环的累积非弹性滞后能△ω和材料常数来确定开始损伤的循环次数。一旦在材料满足损伤起始标准时,则需要基于稳定循环的非弹性滞后能来计算和更新损伤状态。
由于裂纹尖端不可能停留在单元内,只能在边界上,所以对于稳定循环N结束时如果单元的任一裂纹尖端均满足裂纹扩展标准,则将从当前循环向前延伸△N个周期,通过压裂使裂纹长度向前延伸至少一个单元,当前循环的损伤变量DN也增大,新的损伤变量DN+△N由下式给出:

式中:L为单元节点相关的特征长度,c3和c4为材料常数。
通过指定损伤外推公差△Dtol,使用自适应算法基于下式来确定损伤外推的周期数:

如果最大损伤增量大于指定的损伤外推公差,则向前推出损伤的循环次数相应减少,以确保最大损伤增量小于损伤外推公差。反之如果所有材料点的最大损伤增量小于指定的损伤外推公差的一半,则循环次数相应增加,以确保最大损伤增量等于损伤外推公差。

图2 预置裂纹的叶片模型Fig.2 The blade model with pre-crack
2.3 舰船蒸汽轮机叶片裂纹扩展数值模拟
在损伤起始标准中,选用POWER准则来计算临界应变能释放率,其表达式为:

其中:Gequiv为等效应变能释放率。 GIC、GIIC、GIIIC为沿三个方向的剪切模态断裂能量。arn、ars和art为各幂指数。
本文选取实际舰船蒸汽轮机叶片来进行裂纹扩展模拟,并在叶片上预置裂纹,如图2所示。
叶片材料选择2Cr13,其主要参数如表1所示。
参考舰船蒸汽轮机叶片实际的工作过程,不考虑温度引起的热应力的影响,对叶片施加旋转载荷条件,旋转半径414 mm,大小为2 500弧度/分析步,步长设置为3 000步。计算结果如图3所示。

表1 2Cr13材料参数Tab.1 2Cr13 material parameters

图3 始末状态的应力云图Fig.3 Stress cloud charts of beginning and end
裂纹扩展过程中的应力云图和塑性应变累积过程如图4所示。
图4(a)为叶片裂纹扩展过程中的应力变化云图,从图中可以看出应力集中基本发生在已完全裂开单元的上下表面和裂纹尖端,当循环达到1 075次时,由于此时裂纹长度较长,叶片有效承载面积较小,整个叶身的有效应力处于较高水平。图4(b)为累积塑性应变云图,同应力云图一样,塑性应变区集中在裂纹上下表面以及裂纹尖端,随着叶片损伤程度的增加,在保持循环内外载荷不变的情况下,塑性应变量也大幅增加。
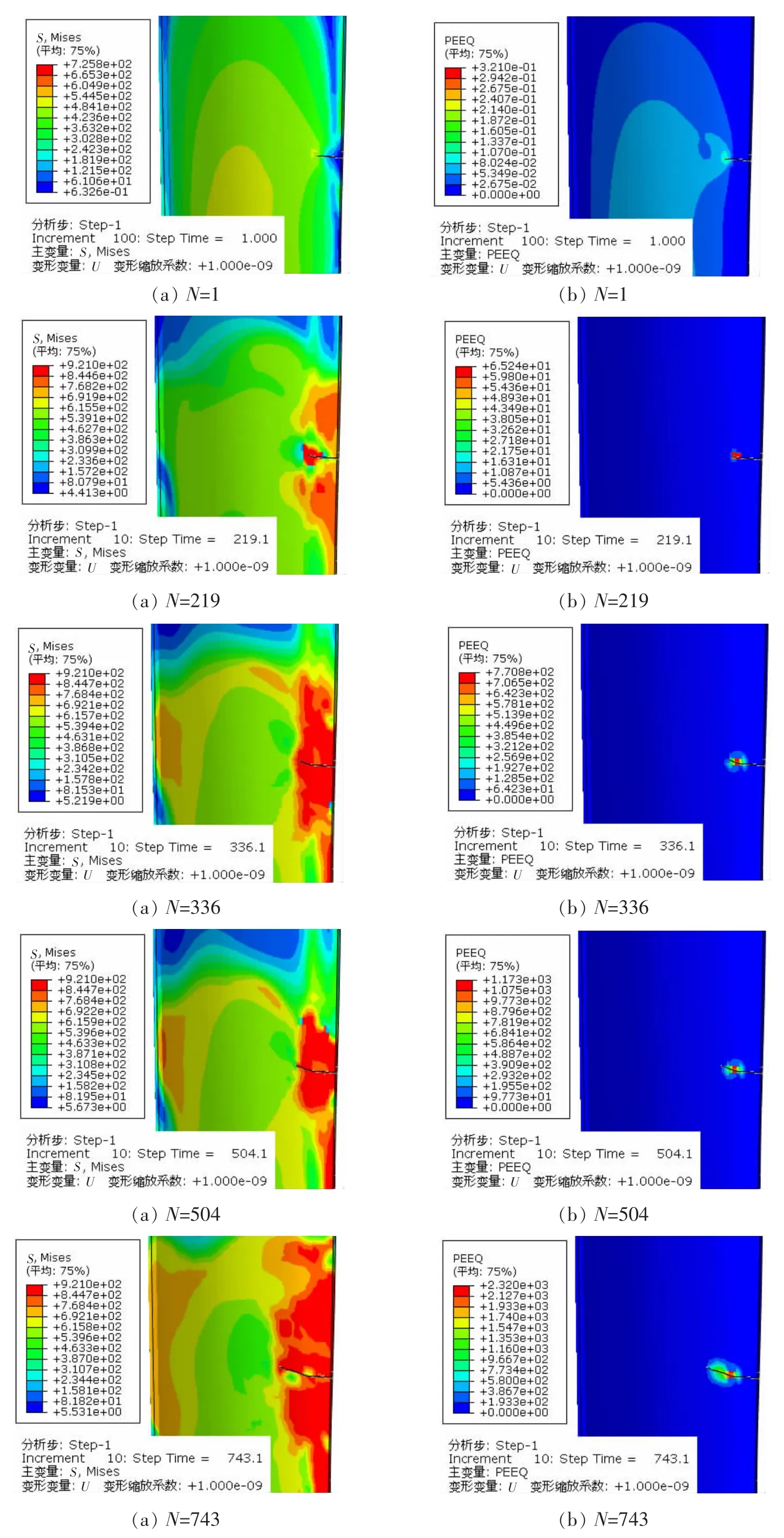

图4 (a)应力云图;(b)累计塑形应变云图Fig.4 (a)Stress cloud charts;(b)Cumulative plastic strain cloud
3 结果分析
ABAQUS模拟裂纹扩展时每次向前推进至少一个单元,且裂纹尖端一般都在网格界面处,因此,对于整个叶片的损伤变量可以通过已断裂的网格面积和叶片横截面积的比值来确定。表2和图5给出了裂纹扩展模拟时损伤变量与循环次数的对应关系。
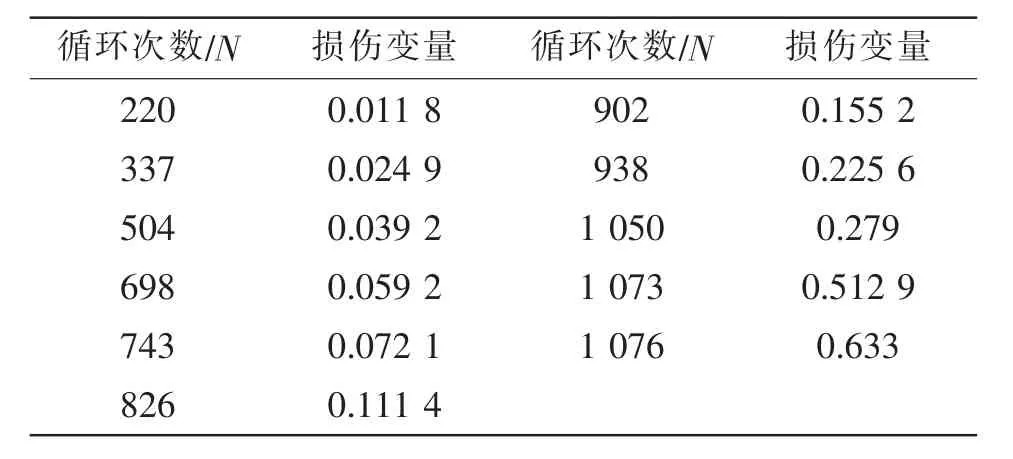
表2 N次循环后的损伤值Tab.2 The damage value after N times cycle
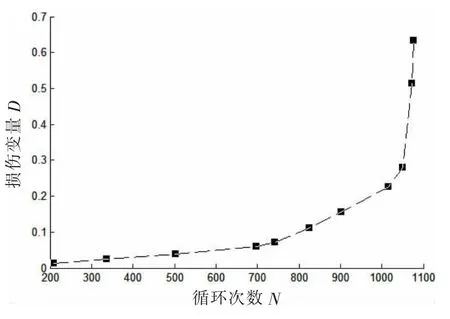
图5 损伤随循环次数的变化曲线Fig.5 Damage curve with the number of cycles
由于载荷较大,当材料进入塑性区时,随着塑性的逐渐积累,ABAQUS在每一个循环加载后会出现由于塑性引起的残余应力场,这使得循环特性的值不为0,间接影响平均应力的大小。
选择初始循环中裂纹尖端位置的前缘单元的应力状态作为理论计算的基础。峰值应力出现在载荷达到最大时,大小为533 MPa,谷值应力出现在载荷卸载后的残余应力场,大小为403 MPa,同时可计算出三轴应力Rv为1.79。
根据损伤增量的表达式来确定材料常数S,即:

通过ABAQUS输出材料随循环加载得到的累积塑性应变,得出S≈89 MPa。
将上述值代入(9)式中,可得叶片的低周疲劳寿命约1 132次。将计算结果与ABAQUS模拟结果对比如图6所示。
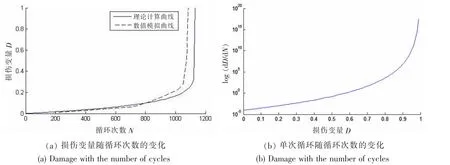
图6 损伤过程变化曲线Fig.6 Damage process curve
从上图可以看出,数值模拟曲线与理论计算曲线结果基本相近,误差约为5%左右。同时曲线变化的趋势大致相同,在损伤变量小于0.1之前,材料的损伤程度随着循环次数呈现近似比例增长,且斜率较小。达到损伤门槛值前后时,损伤的增长速率逐渐增加,直到损伤变量达到0.3左右时,较高的应力集中程度使得材料进入严重塑性区,叶片失去作用而迅速断裂,此时模型曲线也接近垂直于横轴。
4 结 论
本文基于损伤力学的基本理论给出了叶片低周疲劳寿命的计算方法,考虑实际叶片的受力情况以及材料塑性应变的影响,在公式中加入平均应力进行修正。同时基于XFEM方法模拟叶片裂纹扩展过程,分析了低周疲劳寿命,得出以下结论。
(1)本文给出了计算叶片低周疲劳寿命的数学模型,并在考虑叶片实际非对称循环的工作状态下,引入平均应力的概念对模型进行了修正。
(2)使用该模型计算低周疲劳寿命的结果与数值模拟的结果相比基本接近,误差约在5%。
(3)材料损伤程度达到损伤门槛值0.094前,单次循环内损伤增量较小,损伤变量随循环次数变化幅值较小,此阶段大致占总寿命的80%;损伤达到临界值以后,单次循环内增量迅速提高,材料进入严重的塑性变形区,进而迅速失效,表现为叶片断裂。
参 考 文献:
[1]朱宝田,刘东远.计算汽轮机叶片低周和高周疲劳寿命的改进的局部应力应变方法—第一部分 模型与方法[J].热力发电,1997(04):9-14.Zhu Baotian,Liu Dongyuan.Improved local stress-strain method for calculating low cycle and high cycle fatigue life of steam turbine blades-part I models and methods[J].Thermal Power Generation,1997(04):9-14.
[2]朱宝田,刘东远.计算汽轮机叶片低周和高周疲劳寿命的改进的局部应力应变方法—第二部分 计算和分析[J].热力发电,1997(05):3-8.Zhu Baotian,Liu Dongyuan.Improved local stress-strain method for calculating low cycle and high cycle fatigue life of steam turbine blades-part II calculation and analysis[J].Thermal Power Generation,1997(05):3-8.
[3]陈沙古,黄进浩,万正权,卞如冈.基于损伤演化的裂纹扩展寿命简化计算方法[J].船舶力学,2014,18(07):815-820.Chen Shagu,Huang Jinhao,Wan Zhengquan,Bian Rugang.Research on calculation method of crack propagation life based on damage evolution[J].Journal of Ship Mechanics,2014,18(07):815-820.
[4]张 鼎,黄小平,崔维成.一种复杂载荷作用下船舶结构疲劳裂纹扩展预报方法[J].船舶力学,2015,19(05):541-552.Zhang Ding,Huang Xiaoping,Cui Weicheng.A procedure to predict fatigue crack growth of ship structures under complex loading condition[J].Journal of Ship Mechanics,2015,19(05):541-552.
[5]Lemaitre J.损伤力学教程[M].北京:科学技术出版社,1996.Lemaitre J.Damage mechanics tutorial[M].Beijing:Science and Technology Press,1996.
[6]周胜田.航空发动机叶片疲劳的损伤力学研究及外物损伤影响[D].沈阳:东北大学,2008.Zhou Shengtian.Study on fatigue of air-engine blades by damage mechanics and infulence of object damage[D].Shenyang:Northeastern University,2008.
[7]刘晓燕,何晓梅,董 洁.2Cr13钢的疲劳裂纹萌生与扩展行为[J].热加工工艺,2012(02):51-54.Liu Xiaoyan,He Xiaomei,Dong Jie.Fatigue crack initiation and propagation behavior of 2Cr13 steel[J].Hot Working Technology,2012(02):51-54.
[8]孙 勇.基于Monte-Carlo法的燃气轮机压气机叶片可靠性分析[D].哈尔滨:哈尔工业大学,2015.Sun Yong.Reliability analysis of gas turbine compressor blade based on Monte-Carlo method[D].Harbin:Harbin University of Technology,2015.
