对旋转棱镜法和旋转齿轮法测光速的讨论

李忠相 胡馨月 李思衡 张伦铭

(重庆市第一中学校，重庆 400030)

真空中的光速是物理学基本常数之一．1973年确定的国际标准值为c=299 792 458 m/s,1983年第17届国际计量大会决定,将光在真空中1/299 792 458s内运行路程的长度作为“m”的新定义．1986年,国际科技数据委员会又规定1973年的光速国际标准值为精确值．

光速的测定在物理学史上有非常特殊而重要的意义，它不仅推动了光学实验的发展,打破了光速无限的传统观念,也为粒子说和波动说的争论提供了判定的依据,而且最终推动了爱因斯坦相对论理论的发展．历史上,光速的测定花费了好几代物理学家的心血,方法不断改进,测量结果越来越精确,这些巧妙的实验中蕴含了十分丰富的教学价值,但大多数教材都只是一带而过．近日,在面向九年级资优学生的讲座中对旋转棱镜法和旋转齿轮法测光速进行了尝试性挖掘,取得了较好的效果．于是我们把几个相关问题及其讨论整理成此文,与大家分享．

题目.图1给出了历史上测量光速的两种经典装置简图．其中甲图为旋转棱镜法,乙图为旋转齿轮法．请据此完成以下问题:

(1) 阐述两种测量方案的测量原理和测量步骤;

(2) 两种测量方案需要分别记录哪些物理量,并给出计算光速的相应表达式;

(3) 结合实际情况,对两种方案的优劣进行对比;

(4) 查阅相关史实,了解光速测定的历程,体会光速测定的艰辛和成就．

通过学生独立思考、相互讨论和教师引导,当堂完成了前3个问题．第(4)问留作课后作业,一周之后作了交流讨论．通过讨论,对这两个实验有了更深入的认识．

甲 旋转棱镜法

乙 旋转齿轮法

1 测量原理和步骤

1.1 旋转棱镜法

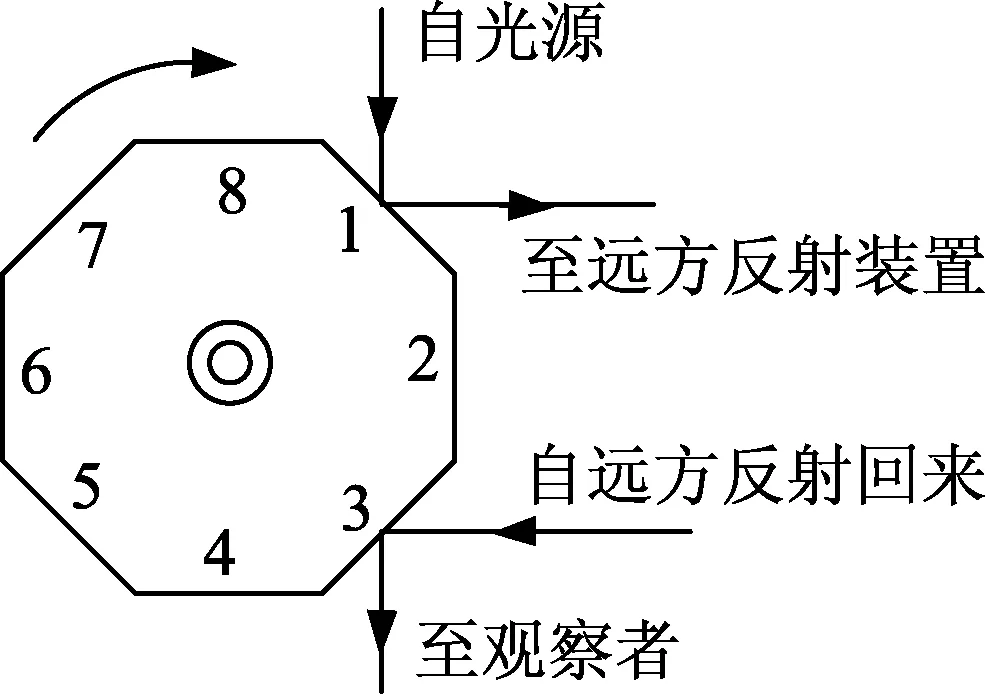
图2 旋转棱镜法原理

测量原理:如图2所示,棱镜不转动时,只有八棱镜的某一面(如图中的1号面)恰好与入射光线成45°角时,光线能被反射至远方的反射装置,反射回来的光线经3号面反射进入观察者眼睛,观察者能看到光源的像．棱镜以较小的转速转动时,光线经1号面和反射装置反射后到达棱镜时,3号面已经不再与光线成45度角,光线无法进入观察者眼睛,观察不到光源的像．若缓慢提高棱镜转速,当光线反射回棱镜时,棱镜刚好转过1/8转,即2号面转至原3号面所在位置,则光线又可以进入观察者眼睛,重新看到光源的像．

测量步骤:先在棱镜不转动的情况下,调节棱镜和反射装置,使观察者能看到光源的像．缓慢提高棱镜转速,当再次看到光源的像时,即达到目标转速．在目标转速下,理论上看到的应该是不断闪烁的像,但闪烁间隔通常非常小,由于视觉暂留,实际看到的是光源“持续”的像．

1.2 旋转齿轮法

测量原理:实验中选用齿宽和齿间缝宽相等的齿轮,当齿轮匀速转动时,光线周期性被齿轮遮挡,穿过光线的光强随时间变化规律如图3中甲所示．这些光线由反射装置反射回齿轮处时,具有一定的延时,光强随时间变化规律如图3中乙所示．返回的光线被齿轮部分遮挡,如图3中阴影部分．若进一步提高齿轮转速,则齿轮透光时间和挡光时间均减小,反射光线中被遮挡的比例增大(如图3中丙所示)．当其减小到刚好等于光线反射延时(如图3中丁所示),反射光线刚好全部被遮挡,观察者刚好看不到光源的像．

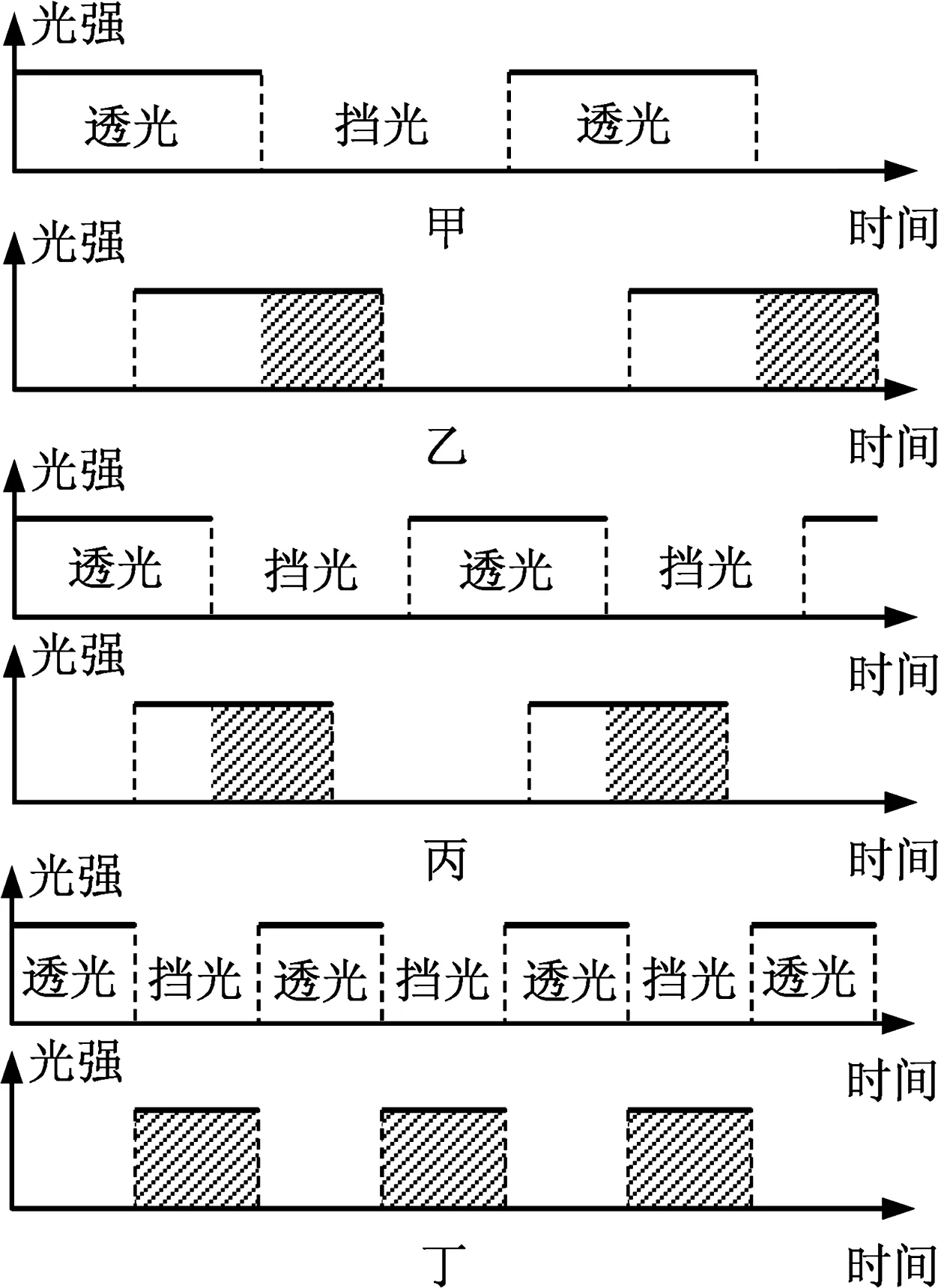
图3 旋转齿轮法原理

测量步骤:先在齿轮不转动的情况下,调节齿轮和反射装置,使观察者能看到光源的像．缓慢提高齿轮转速,光源的像逐渐变暗,当看到光源的像第一次完全变暗时,即达到目标转速．

2 待测物理量和计算公式

2.1 旋转棱镜法

由前述测量原理可知,该实验需要测量反射装置到棱镜的距离L,目标转速n(以“r/s”为单位),由于光在距离L上一个来回的时间内棱镜刚好转过八分之一圈,有

(1)

得

c=16nL.

(2)

2.2 旋转齿轮法

(3)

得

c=4nNL.

(4)

3 两种方案的对比

3.1 实验现象及精度

旋转棱镜法中,棱镜转速只有在目标转速附近极小的范围内可以看到光源的像,其他转速下均观察不到光源的像．虽然理论上目标转速的整数倍处也能看到光源的像,但目标转速非常大,其整数倍几乎难以实现,故不做考虑．所以,在此实验中,实验现象稍纵即逝,难以被观察到．而一旦被观察到,对应的转速会比较精确,测量结果精度较高．

旋转齿轮法中,齿轮转速在接近目标转速的过程中,看到光源的像逐渐变暗,转速超过目标转速后,像又逐渐变亮．所以,在此实验中,实验现象容易被观察到．但在目标转速附近,像的亮度小到观察者无法识别时会和目标状态混为一体,于是目标转速的不确定度便增大了,降低了实验精度．

3.2 实验条件

光速难以测量主要是因为光速数值太大,由公式(2)和(4)不难发现,实验需要尽可能大的反射距离L和转速n．考虑到光束的发散、损耗等因素,距离L不能无限制增加,若两个方案使用相同的距离L,增大齿轮齿数可以显著降低对转速的要求,但八棱镜却受限于加工精度不便于随意增加镜面数,所以旋转齿轮法在实验条件上具有优势．

4 对旋转齿轮法计算公式的修正

当齿轮不转动时,观察者看到光源的像是连续存在的,将其亮度记为I0;当齿轮转动时,像的亮度降低．若观察者能识别的最小亮度为αI0(α为小于1的常数),当转速增大到某一值(记为n1)时像刚好无法识别,转速继续增大到另一值(记为n2)时重新观察到像．那么,目标转速n能否由n1和n2确定?

如图4甲所示,当齿轮齿数为N，转速为n1时,透光时间和挡光时间均记为ΔT,有

图4 旋转齿轮法像的亮度

(5)

光线在距离L上一个来回用时记为Δt,有

(6)

观察者观察到像的亮度αI0与齿轮不转动时像的亮度I0之比等于一个周期内反射光的透光时间与周期2ΔT之比,即

(7)

由(5)～(7)式可得

(8)

同理,可得当转速为n2时,有

(9)

由(8)、(9)式可得

c=2(n1+n2)NL.

(10)

此即为考虑到观察者分辨临界后的光速计算公式．与(4)式对比可知,目标转速n和n1、n2的关系为

(11)

可见,在亮度减小和增加时观察阈值一样的假设下,利用(10)式可以提高测量精度．

5 一些相关史实

1849年法国人斐索(A.H.Fizeau)用旋转齿轮法(即图1乙所示)测得光速为3.153×108m/s．成为在地面上用实验方法测定光速的第一人．旋转齿轮法能率先取得成功但误差相对较大,和前文对于实验现象和精度的分析结论一致．当时采用的距离大约8 km,齿轮齿数720,所需转速大约13r/s,这在当时通过机械装置是可以实现的．

图5 傅科用旋转镜法测光速

1862年法国人傅科(J.L.Foucault)用旋转镜法测量空气中光速为2.98×108m/s．旋转镜法(如图5所示)是本文所述旋转棱镜法的前身,实验难度很大但精度较高．

1874年考尔纽(A.Cornu)改进了斐索的旋转齿轮法,取得更精确的结果,即2.999×108m/s．由改进方案,成功地提升了旋转齿轮法的测量精度．

1879年美国物理学家迈克尔逊(A.A.Michelson)又改进了傅科的旋转镜法,测得光速为(2.999 1 ± 0.000 5)×108m/s．迈克尔逊的实验非常精湛,他把毕生精力沉浸在光学实验中,以光速精密测量为己任,40多年后,他把方法逐渐发展为旋转棱镜法(即图1甲所示),1926年他用棱镜的相反两面发送和接收信号(如图6),在相距35km的两山之间,测得光速的结果为(2.997 96 ± 0.000 04)×108m/s．这个实验免除了旋转镜法中对角度测量的偏差,进一步提高了测量精度．

图6 迈克尔逊手绘的光速测量示意图(1926年)

参考文献：

1 郭奕玲,沈慧君.物理学史(第2版)[M].北京:清华大学出版社,2005:140-144.

2 弗卡约里.物理学史[M].桂林:广西师范大学出版社,2008:118-122.