精密线切割电加工建模仿真研究
2018-04-25张宏达
张宏达
(宝鸡职业技术学院 陕西 宝鸡 721013)
引言
当前,随着我国制造工业的不断发展,对精密模具的要求也变得越来越高。比较典型的如汽车方向盘、保险杆,以及空调、洗衣机等电器,都对模具的精度提出了更高的要求。要生产高精度的模具,加工过程控制是关键,也是当前研究的难点。如在一般的模具生产中,其精度要求在3~5 μm,但是部分模具精度要求,则需要达到1~2 μm的精度。模具精度的提高,对工件加工设备提出了更高的要求,特别是在精加工阶段。实践认为在模具加工的整个阶段,精加工所耗费的时间最长,若可以提高模具加工的效率和精度,不仅可以缩短整个加工时间,缩短模具交货的周期,还可以节省部分工序。而根据部分专家对模具市场的预测,在未来我国模具精度将提高到1 μm以下的水平。
电火花线切割加工(WireCutEDM,简称WEDM),被认为是一种借助火花放电的方式,对需要加工的工件进行切割的技术[1]。在电火花放电的过程中,放电时间通常都比较短,通常以μs的时间来计算,并且在放电的过程中,伴随着比较复杂的物理过程,即短时间之内会形成高温,并蚀除工件表面的材料,进而达到对精度的控制。这种切割加工方式具有可控性好,工艺精度高等特点,从而被广泛地应用在复杂零件,或者是一些高硬度材料的加工中。同时随着现代加工对精度的要求,如何提高电火花切割中工件加工的精度,对提升整个加工行业的水平具有重要的价值和意义。当前针对电火花加工的研究中,主要集中在两个方面:一是对影响电火花加工的影响因素进行研究,进而对工艺参数进行优化。如A&M大学的Philip T.Eubank等人[2]则根据热动力学等理论构建等离子体柱电加工模型,构建阴、阳蚀除模型,进而对加工过程进行仿真,影响EDM蚀除的主要原因是因为过热的问题。哈尔滨工业大学的崔景芝则结合电火花加工的基本规律[3],以分子运动学作为研究基础,对针尖钨的放电加工过程进行了模拟,进而验证了在放电过程中的影响因素;二是在上述研究基础上,部分学者提出提高加工精度的方法,如华中科大的明五一博士在其发表的博士论文中[4],则提出通过多目标优化的方式对工艺参数进行优化,进而提高加工精度。江晖则针对壳体底部均布三处复杂沉窝加工中存在的难题提出:提高电极的制造精度,同时优化工艺参数的方式,进而提高粗加工精度。本文则在上述研究的基础上,提出一种基于人工智能算法的切割工艺参数优化模型,并对其加工精度进行仿真验证。
1 神经网络算法的提出
在电火花切割加工过程中,影响切割加工工艺的参数很多,明五一通过研究认为[4],影响电火花加工工艺的参数主要包括材料去除率及表面粗糙度等,并通过建立回归模型的方式就材料去除率和表面粗糙度与加工精度的关系进行建模;英国伯明翰大学的Bayamglu等[5]就主轴转速及电极相对损耗等对切割精度的影响进行了探讨。但随着现代智能算法的发展,Hsue,Liao等开始将智能算法应用到电火花切割加工中[6],对切割过程中的工艺参数进行优化。其中,BP神经网络算法作为现代人工智能算法的典型代表,更是被广泛的研究。
BP网络是一种多层前馈网络,主要包括输入层、隐含层和输出层[7]。如图1所示为典型的三层结构的神经网络。
通过图1看出,在神经网络结构中每个神经元都和下层的神经元保持联结,其中的箭头则表示神经元之间的信息流动方向。当通过输入层输入相关的参数后,经隐含层传递给输出层,输出层再根据输出结果与实际结果之间的误差,通过反向传递的方式传回到输入层,并逐步对连接点的权重进行修正。通过这种反复的修正,最终将输出结果调整到误差范围内,并结束学习训练过程。
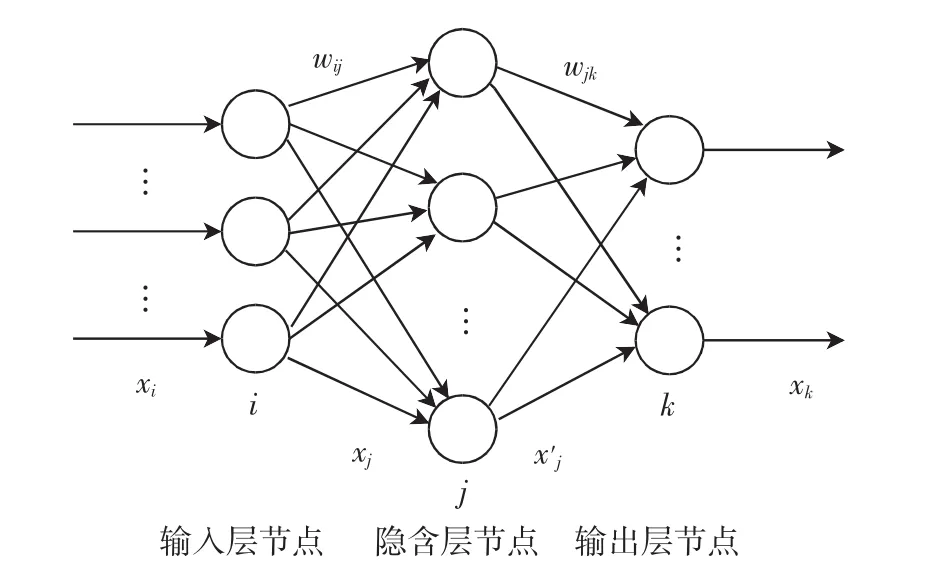
图1 典型的BP网络结构模型
2 基于BP神经网络的电火花线加工模型构建
2.1 参数选取
结合对BP神经网络的分析看出,要完成对电火花线切割加工的精度控制,首先要对影响电火花切割的参数进行验证。根据当前对电火花线切割的研究发现,影响其切割精度的参数很多。本文结合以往的研究基础,选择表1所示的研究参数。

表1 加工模型参数选取

2.2 隐含层节点设计
对BP神经网络来讲,最为关键的一个问题就是对隐含层中的节点进行设计。如果节点过少,会造成学习模型容量有限,进而影响训练的效果;如节点过多,则会导致计算时间过长,从而影响模型的效率。对此,在本文中则借鉴隐含层节点参考公式,对隐含层节点进行计算。

其中,切割速度计算为:
其中:n表示输入层的节点数;m表示隐含层节点的数目;l表示输出层节点的数目,a表示为常数。
根据以往研究的经验,在对隐含层数量的确定取值中,大部分集中在6~15个节点数之间。为确定最佳的隐含层节点数目,本文通过网络训练的方式对节点数进行确定。训练的目标误差设定为0.000 5,当达到这个训练目标,则停止训练。由此可以得到表2所示的网络训练误差。
通过上述的训练看出,当隐含层的节点数在9和14的情况下,其训练误差符合要求。同时比较两个节点数的迭代次数发现,节点数在14的情况下,其迭代次数最少,为5次。由此,本文在对隐含层的选取中,则选择14个节点。
2.3 基于BP的电火花切割加工模型构建
根据上述的分析,加工模型设计如图2所示。

表2 网络训练误差

图2 电火花切割加工网络模型构建
3 模型仿真验证
3.1 训练流程设计
在对模型进行仿真前,需要对BP网络训练的流程进行设计,从而更好地完成仿真。结合BP神经网络的操作,具体的操作流程设计如图3所示。
3.2 试验参数设定
为验证上述方案的可行性,以某中走丝切割数控系统为例,同时以Cr12材料的加工作为试验材料。在具体的切割参数上,将电火花的切割参数设计如表3所示。
3.3 仿真实验结果
对上述参数的仿真,以MATLAB软件进行编程,同时采用正交实验法选取部分组合对预测结果与实际结果进行验证。在仿真训练样本选取方面,选取20组实验数据,其中15组为训练样本,5组为实验样本。通过选取合理的传递函数等,可以得到表4所示的仿真结果。
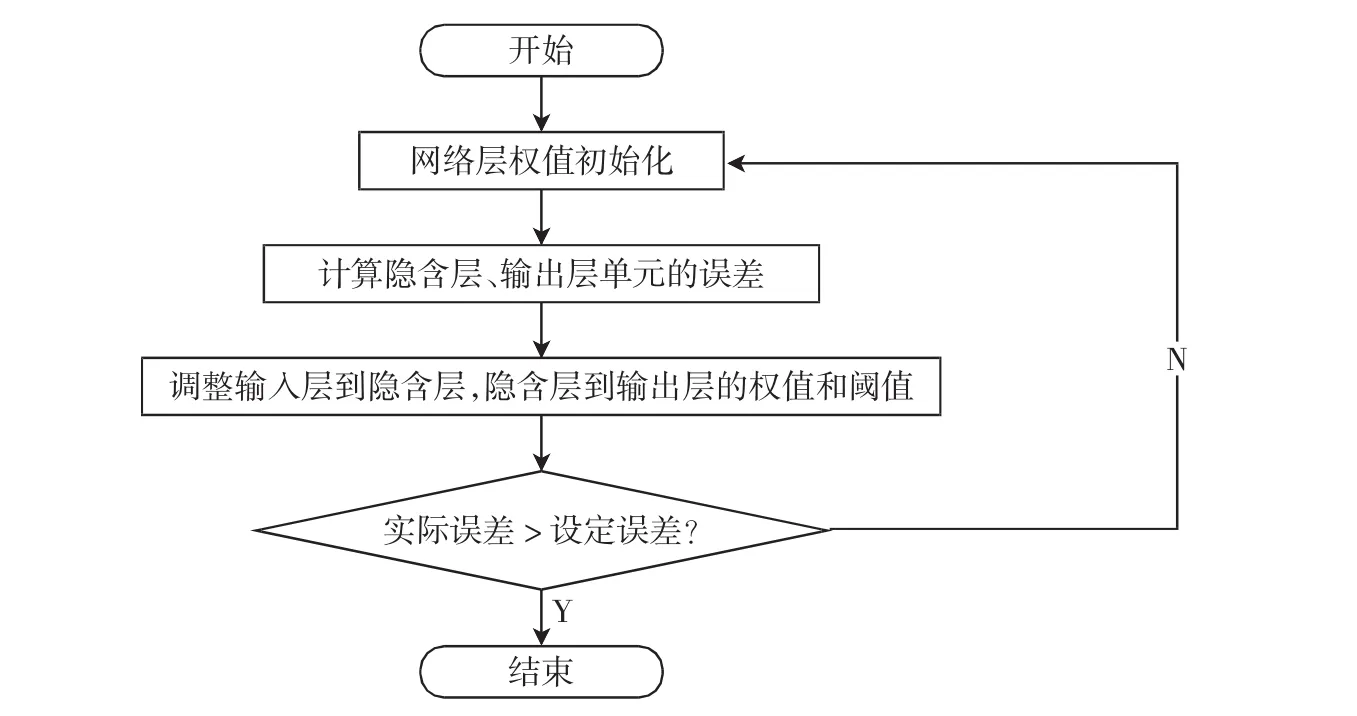
图3 BP网络训练具体流程

表3 电火花切割加工参数

表4 实验因素及结果对比
3.4 结果分析
通过表4的结果看出,采用BP神经网络可及时预测电火花切割线的切割速度和表面粗糙度,并且预测值大部分都与实际值的相差不大。由此可以看出,在电火花切割加工中,引入神经网络算法具有一定的可行性。
4 结束语
通过上述的试验看出,神经网络算法可以有效建立电火花加工切割参数与切割速度和表面粗糙度之间的关系,并通过该模型可对上述结果进行预测,并通过预测的结果来看,与实际值相差不大,大部分都在9.8%的范围之内,从而得出神经网络算法对该加工精度控制的有效性和可行性。
1 陆程,甄敬然.线切割加工连续脉冲放电电极丝三维振动分析[J].机械设计与制造,2015(5):130-133
2 Philip T.Eubank,Mukund R.Patel,Maria A.Barrufet,et al.Theoretical models of the electrical discharge machining process.III.The variable mass,cylindrical plasma model[J].J.Appl.Phys.1993,73(11):7900-7909
3 崔景芝,闫文艳.压路机BYD3313箱体铸造工艺[J].金属加工(热加工),2012(21):16-17
4 明五一,郭建文,张臻,等.精密线切割加工关键理论研究进展综述[J].机电工程技术,2014,43(5):10-13
5 M.Bayamoglu,A.W.Duffill.Systematic investigation on the use of cylindrical tools for the production of 3D complex shapes on CNC EDM machines[J].Int.J.Manufact,1994,34(3):327-339
6 Hsue W.J.,Liao Y.S.,Lu S.S.Analysis and control for wire-EDM roughing-stage conner cutting[J].Bulletin of College of Engineering,N.T.U.1999,75:71-89
7 焦李成,杨淑媛,刘芳,等.神经网络七十年:回顾与展望[J].计算机学报,2016,39(8):1697-1716
