漫谈因式分解的方法与技艺

◎吴文忠

把一个多项式写成几个整式的积的形式，这种变形叫做多项式的因式分解，也叫做把这个多项式分解因式.因式分解是中学数学中最重要的恒等变形之一，它被广泛地应用于初等数学之中，在求根作图、解一元二次方程方面也有很广泛的应用，是解决许多数学问题的有力工具.因式分解方法灵活，技巧性强.学习这些方法与技巧，不仅是掌握因式分解内容所必需的，而且对于培养解题技能、发展思维能力都有着十分独特的作用.学习它，既可以复习整式的四则运算，又能为学习分式打基础；学好它，既培养了观察、思维、运算能力，又提高了综合分析和解决问题的能力.常见的因式分解方法有：提公因式法、公式法、分组分解法、十字相乘法等.

一、提公因式法

如果一个多项式的各项有公因式，可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提公因式法.

例1 分解因式：-2m3+8m2-2m.

【分析】当各项系数都是整数时，公因式的系数应取各项系数的最大公约数；字母取各项的相同的字母，而且各字母的指数都取次数最低的.如果多项式的第一项是负的，一般要提出“-”号，使括号内的第一项的系数成为正数.提出“-”号时，多项式的各项都要变号.

解：原式=-2m·m2-2m·（-4m）-

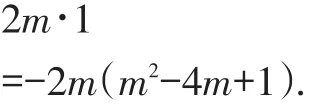
【点评】提完公因式后，另一个因式的项数与原多项式的项数相同；注意2a+1=不是提公因式，因为括号内不得出现分数.提公因式法可以用一句话来概括：找准公因式，一次要提尽，全家都搬走，留1把家守，提负要变号，变形看奇偶.

二、公式法

如果把乘法公式的等号两边互换位置，就可以得到用于分解因式的公式，用来把某些具有特殊形式的多项式分解因式，这种分解因式的方法叫做公式法.

平方差公式：a2-b2=（a+b）（a-b）；完全平方公式：a2±2ab+b2=（a±b）2.

例2 （2017·无锡）分解因式：3a2-6a+3.

【分析】能运用完全平方公式分解因式的多项式必须是三项式，其中有两项能写成两个数（或式）的平方和的形式，另一项是这两个数（或式）的积的2倍.

解：原式=3（a2-2a+1）=3（a-1）2.

【点评】提完公因式后，再运用完全平方公式继续分解因式.公式法也可以用一句话来概括：首平方，尾平方，积的二倍放中央；同号加、异号减，符号添在异号前.

三、分组分解法

通过分组分解的方式来分解的因式一般有四项或大于四项，一般的分组分解有两种形式：二二分法，三一分法.初中教材中只是作为阅读内容供同学们课外了解、研究，没有作为必学内容展开.

例3 分解因式：ac+bc+3a+3b.

【分析】可以把ac和bc分为一组提取公因式c，3a和3b分为一组提取公因式3，最后再提取公因式（a+b）.

解：原式=c（a+b）+3（a+b）=（a+b）（c+3）.

【点评】当然也可以把ac和3a分为一组提取公因式a，bc和3b分为一组提取b，最后再提取公因式（c+3）.一定要合理分组.

四、十字相乘法

十字相乘法在初中教材中没有涉及，但在高中的数学学习中运用得非常多.它有两种情况：①x2+（p+q）x+pq型的因式分解，这类二次三项式的特点是：二次项的系数是1，常数项是两个数的积，一次项系数是常数项的两个因数的和.因此，可以直接将某些二次项的系数是1的二次三项式因式分解：x2+（p+q）x+pq=（x+p）（x+q）.②kx2+mx+n型的因式分解，如果有k=ac，n=bd，且有ad+bc=m时，那么kx2+mx+n=（ax+b）（cx+d）.图示如下：

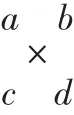
例4 分解因式：2x2-5x-3.

【分析】对于不能用提公因式和公式法来分解的二次三项式可考虑用十字相乘法.

1×1=1，-3×2=-6，且-6+1=-5，

所以2x2-5x-3=（x-3）（2x+1）.

【点评】运用十字相乘法分解因式时，先不断尝试拆分首尾数，可以用一句话来概括：首尾分解，交叉相乘，求和凑中间.

因式分解没有普遍适用的方法，初中数学教材中主要介绍了提公因式法、运用公式法、分组分解法，在分解因式时要根据题目的具体情况而定.多项式因式分解的一般步骤：①如果多项式的各项有公因式，那么先提公因式；②如果各项没有公因式，那么可尝试运用公式、十字相乘法来分解；③如果用上述方法不能分解，那么可以尝试用分组、拆项、补项法来分解；④分解因式，必须进行到每一个多项式的因式都不能再分解为止.因式分解也可以用一句话来概括：先看有无公因式，再看能否套公式；十字相乘试一试，分组分解要合适”.而在竞赛上，又有拆项和添减项式法、换元法、长除法、短除法、除法等，同学们可根据自身学习的需要进行有选择的研究.