卡西欧计算器在高职平差课程中的应用探讨

（甘肃建筑职业技术学院，甘肃 兰州 730050）

测量平差是高职院校工程测量技术专业的一门专业基础课程，该课程的教学效果与质量对工程测量技术专业学生的培养质量至关重要，同时也是学生反映最难学懂、学会的课程。结合高职学生实际情况，将卡西欧计算器引入平差教学中，对该课程的教学改革进行探讨。

1 平差课程教学问题

高职院校不同于本科的教学，学生适度掌握理论，能够进行数据的基本平差计算即可。但平差课程涉及高等数学、线性代数、概率论等数学知识，只有掌握以上课程才能良好地进行平差课程的学习。而近年来职业院校的录取方式更加多元化，有单独考试招生、高考统招、中职转段等，学生来源不同，部分学生数学基础非常薄弱，基础数学课程的学习当中存在诸多问题，导致学生学不懂、学不会。

平差课程涉及大量的线性代数矩阵计算，计算工作繁多，学生在计算时会有耗时长、计算很吃力、计算错误、甚至不会计算等现象发生，学生逐渐失去学习热情，进而对课程产生厌学情绪，最终导致平差课程很难实现应有的教学目标。提高学生数学能力有赖数学教师的努力，测量教师应与数学教师沟通，希冀其将平差课程中用到的数学知识作为重点进行讲授。但更加重要的是如何在学生现有数学基础上进行平差课程的教学，此为课程改革的一项研究内容，以往主要通过以下方向进行改革[1]。

1.1 使用平差软件

将平差易、科傻等平差软件，引入教学过程，进行实践操作，但平差软件注重数据的输入和平差结果的输出，学生不能看到数据的具体处理过程，与教学目标不符。

1.2 使用数学建模软件[3][4]

与线性代数改革类似[2]，平差教学中使用数学建模软件Matlab进行矩阵的基本计算，进而使用M语言进行编程计算。采用此种方式能够避免繁琐的计算，但在课程学习中需要学生掌握编程的基本知识，而编程同样是高职学生学习的一个难点。此外，学生课后练习时需要配备电脑，而部分学生受经济条件、院校受教学条件限制，不能满足要求，因而不能即时进行计算。

2 卡西欧计算器教学优点

CASIO fx-5800计算器自2006年面市以来，以价格经济、易于携带、编程简单等特点，在工程测量中得到广泛应用，尤其是在道路、桥梁、隧道平面施工放样的计算方面[5]。部分院校紧跟该趋势，在施工测量课程计算中采用计算器进行计算或者开设卡西欧计算器编程方面的课程，取得良好效果，但在平差课程的教学中鲜有使用。

CASIO fx-5800有Mat A～F、Mat Ans等七个矩阵存储器，能够进行10×10矩阵的计算，计算方便、快捷，学生在很短的时间内能够熟练使用七个基本功能，无论在课堂还是课后练习中，能够随时进行计算。且价格低廉，学校很容易能够为学生配备，能够满足平差课程的教学需要。

2.1 间接平差算例

以教材[6]中水准网间接平差为例，水准网中A、B的高程分别为HA=5.000m，HB=6.008m，P1、P2、P3为未知点，观测值及路线长度见表1，求待定点的平差值并进行精度评定。

表1 观测值及路线长度

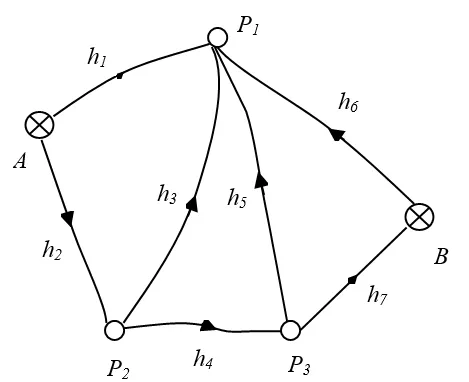
图1 水准网图形

2.2 误差方程

误差方矩阵形式程为

令观测值的权为

2.3 解算法方程

用计算器矩阵存储器Mat A存储矩阵P，Mat B存储矩阵B，Mat C存储矩阵l，在计算器上按键FUNCTION 8 4 FUNCTION 8 2 ALPHA B ） × FUNCTION 8 2 ALPHA A × FUNCTION 8 2 ALPHA B，屏幕显示Trn（Mat B）×Mat A× Mat B，Trn（Mat B）即为BT，执行可得NBB。

按键FUNCTION 8 2 Shift Ans Shift x-1FUNCTION 3 2 FUNCTION 8 2 ALPHA D，屏幕显示 Mat Ans-1→Mat D，执行可得，并储存至Mat D。

按键 FUNCTION 8 4 FUNCTION 8 2 ALPHA B ） ×FUNCTION 8 2 ALPHA A × FUNCTION 8 2 ALPHA C FUNCTION 3 2 FUNCTION 8 2 ALPHA E，屏幕显示Trn（Mat B）×Mat A×Mat C →Mat E，执行可得W，并储存至Mat E。

W =[ 0 16 -12 ]T

按 键 FUNCTION 8 2 ALPHA D × FUNCTION 8 2 ALPHA E FUNCTION 3 2 FUNCTION 8 2 ALPHA F，屏幕显示Mat D × Mat E →Mat F，执行可得δx，并储存至Mat F。

δx = [ 0.7213 3.2131 -0.6885 ]T

2.4 计算改正数及平差值

按 键 FUNCTION 8 2 ALPHA B × FUNCTION 8 2 ALPHA F - FUNCTION 8 2 ALPHA C，屏幕显示Mat B× Mat F - Mat C，执行可得改正数V。

平差值、未知数最或然值即可很容易得到。

2.5 精度评定

单位权中误差

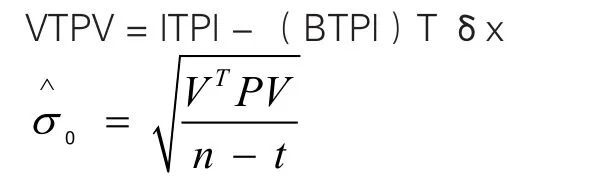
按键 FUNCTION 8 4 FUNCTION 8 2 ALPHA C ） ×FUNCTION 8 2 ALPHA A × FUNCTION 8 2 ALPHA C -FUNCTION 8 4 FUNCTION 8 4 FUNCTION 8 2 ALPHA B） × FUNCTION 8 2 ALPHA A × FUNCTION 8 2 ALPHA C ） × FUNCTION 8 2 ALPHA F，屏幕显示 Trn（Mat C）× Mat A × Mat C - Trn（Trn（Mat B）× Mat A× Mat C）× Mat F，执行得结果28.33，即VTPV。

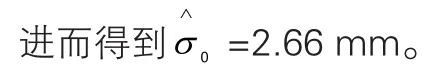
至此，计算过程结束。在上述过程中，学生能够进行基本的矩阵存储、矩阵转置、矩阵求逆等操作即可进行，当其能熟练使用卡西欧计算器时，能够很快完成习题的计算，得到正确的结果。

3 结 语

应用卡西欧计算器进行平差计算，能够将学生从繁琐的计算中“解救”出来，教师只需指导学生列立误差方程、法方程等即可；能够提升学生学习兴趣、提高计算速度、节约学习时间，将精力投入到平差概念、方法的学习当中；同时，为后续的《工程测量》、《卡西欧计算器编程》等课程打好坚实的基础。因此，在平差课程中应用卡西欧计算器，进行相应的课程改革，可以提升平差课程的教学效果，对工程测量技术专业的教学质量起到良好的推动作用。

[1]邓兴升.提高测量平差课程教学质量的措施[J].测绘工程，2010，19(3):74-76.

[2]陈怀琛.线性代数要与科学计算结成好伙伴[J].大学数学，2010，26(1):28-34.

[3]白征东.Matlab在测量平差教学中的应用[J].测绘通报,2009,(11):73-76.

[4]高霞.浅议MATLAB对测量平差教学的启示[J].矿山测量 ,2016,44(02):105-107+110.[2017-10-12].

[5]李爱军.Fx-5800P可编程计算器在连通隧洞施工测量中的应用[J].测绘工程,2011,20(04):70-73+76.

[6]靳祥升.测量平差[M].第二版.郑州：黄河水利出版社，2010.