转捩对某民机超临界机翼影响的数值模拟研究

李鹏飞, 冷智辉, 魏 闯, 任园军, 梁 斌

(1.中国航空工业洪都航空工业集团 飞机设计研究所, 江西 南昌 330024； 2.中国航空工业空气动力研究院 高速高雷诺数重点实验室, 辽宁 沈阳 110034)

0 引 言

超临界机翼因具有优越的气动性能得到了很大的发展，被广泛应用到民机机翼设计中，为民机的发展起到了巨大的推动作用。与常规翼型相比，超临界翼型[1]的上翼面平坦、下翼面后部内凹，在跨声速条件下，超临界机翼表面不可避免的会出现边界层发展与转捩、激波/边界层干扰、激波诱导分离等粘性支配的复杂流动现象，决定了超临界机翼气动性能对粘性的影响较为敏感。

转捩表示边界层由层流流动向湍流流动的转变，是流体力学研究领域中一个十分重要而又非常复杂的难题。跨声速条件下，转捩对超临界机翼的边界层特性、激波位置、流动分离位置等有十分重要的影响[2-4]，尽管19世纪80年代Reynolds就发现了转捩现象，但至今理论上还无法准确地确定转捩点的位置，通过半个多世纪的理论与实验研究，对转捩机理的认识不断深入，发展了许多边界层转捩判断方法，同时随着计算流体力学技术和计算机的发展以及工程应用的需求，用CFD方法进行转捩数值模拟在飞行器气动设计、流动细节及其机理分析中的权重日益提高，成为解决工程实际问题的重要手段[5-8]。预测附面层转捩的方法很多，直 接 数 值 模 拟(DNS)[9]和大涡模拟(LES)[10]耗费计算资源较大，目前主要用于简单流场的模拟，工程上常用的是基于线性稳定性理论的eN方法[11-12]和转捩模型方法[13-14]。鉴于eN方法预测转捩的成熟性，国外很多研究机构将eN方法应用其开发的CFD软件中，如法国宇航院(ONERA)的ELSA[15-16]软件，德国宇航院(DLR)的结构网格求解器FlOWer[17-18]和非结构混合网格的求解器TAU[19]中。国内西北工业大学张坤和宋文萍等采用eN方法，通过精确求解线性稳定性方程来判断二维翼型和无限展长后掠机翼[20-21]边界层转捩，中国航空工业空气动力研究院董军、高德峰、任园军等应用eN方法进行了ONERA M6机翼的工程转捩计算的研究[22]，国内公开文献中对eN方法的研究主要集中在二维翼型和三维机翼标模上，而把eN方法预测转捩用于飞机型号风洞试验现象研究的文献还不多见。

本文利用RANS方程耦合eN-Database转捩预测方法，针对某民机超临界机翼，研究转捩对其激波位置、分离位置等流动特性的影响，分析其在自由转捩试验中升力线小迎角下出现拐折现象的原因及其流动机理，供超临界机翼设计和气动特性分析参考使用。

1 数值计算方法

1.1 eN-Database转捩预测方法

本文数值模拟以可压缩雷诺平均Navier-Stokes方程为主控方程，湍流模型采用在航空计算中有较好精度的的S-A一方程模型，空间离散采用Jameson中心差分加人工粘性，时间推进采用TVD型的显示三步Runge-Kutta推进，通过多重网格技术、隐式残差光顺等方法加速收敛，并将法宇航Perraul、Arnal和Casalis等提出的流向和横向不稳定性eN-Database判断方法耦合到求解器中来实现对转捩点位置的判断。求解过程为，首先进行全湍条件下的流场求解，然后将压力分布和网格信息输入到转捩判断程序中，获得转捩位置，最后将转捩位置回传到流场求解器中进行求解，即可得到自由转捩计算结果，也可人为给定转捩位置回传到流场求解器中实现固定转捩流场计算，该方法详细介绍见文献[22]。

1.2 计算网格

模型为某民机翼身组合体巡航构型，机翼为超临界机翼。网格为结构网格形式，H-O型网格拓扑结构，边界层第一层网格高度为平均气动弦长的2×10-6倍，保证物面yplus<1，向外递增的倍数不大于1.2，空间网格过度均匀，尽可能保证相邻网格之间的比值小于1.4，总网格量约为1070万节点，飞机表面网格见图1。

图1 计算网格Fig.1 Calculational grid

2 计算结果及分析

在中航工业气动院FL-3风洞进行某民机构型的高速测力风洞试验中，发现在自由转捩试验状态下，在0°迎角附近，升力曲线发生了明显的拐折现象，而在固定转捩试验时，升力曲线拐折现象消失，但同迎角时升力减小，为研究产生此异常现象的原因，应用eN方法对风洞试验模型进行数值模拟计算。

2.1 计算和试验结果对比分析

图2给出了计算和风洞试验结果升力系数对比曲线，风洞试验是在中航工业气动院FL-3风洞完成，固定转捩计算和试验给定机翼上翼面转捩位置为7%当地弦长处，下翼面自由转捩，计算和试验状态：Ma=0.8，基于机翼平均气动弦长Re=1.75×106。从中可以看出，全湍计算升力系数最小，同一升力下阻力最大，固定转捩计算升力线相比全湍计算结果基本成向上平移趋势，自由转捩和固定转捩下机翼气动性能差别很大，与固定转捩相比，自由转捩试验升力系数较大，阻力系数较小，计算结果与此趋势一致，只是计算与试验在量值上略有区别，说明本文计算方法是可靠的。

从风洞试验结果可以看出，自由转捩时升力曲线约在迎角-1°到0°之间发生拐折，自由转捩计算预测到了这种现象，约在迎角0°到1°之间升力曲线发生拐折，固定转捩试验和计算升力曲线在迎角0°附近拐折现象消失。

(a) α～CL

(b) CD～CL

2.2 自由转捩升力线拐折流动机理分析

图3给出了迎角-2°～2°固定转捩和自由转捩计算机翼上翼面层流区范围。从可以看出，迎角-2°～0°自由转捩计算层流区范围明显大于固定转捩，亦即转捩位置靠后，结合图2可以看出，此时自由转捩和固定转捩计算升力系数差值较大；迎角0°和1°之间，自由转捩计算转捩位置发生突变前移，迎角1°和2°时自由转捩计算层流区接近固定转捩结果，此时两者计算升力系数差值较小。综合以上分析，机翼上翼面层流区越大，升力系数越大，迎角0°和1°之间，机翼上翼面转捩位置发生突变，升力曲线因而发生拐折。

文献[23]指出对于一个光滑平板的边界层，由层流转变为湍流的转捩Re数一般在2×106～5×106之间，具体数值取决于噪声水平和湍流度。这样，当试验模型的风洞Re数处于这个量级以及翼面具有平坦的压力分布时，翼面上会存在明显的层流边界层。图4分别给出了机翼三个不同站位剖面0°和1°迎角下固定转捩和自由转捩计算摩阻系数和压力系数对比曲线。从中可以看出，迎角0°时机翼上翼面激波上游压力分布较为平坦，自由转捩条件下为层流，内侧机翼因上翼面后部出现激波诱导转捩为湍流，其转捩位置比固定转捩位置明显靠后，而外侧机翼上翼面并未出现激波，转捩位置更靠后，转捩位置越靠前，激波位置就越靠前，超声速区面积随之减小，升力因而减小，这也是迎角0°时，固定转捩下升力系数较自由转捩小很多的原因。迎角1°时，机翼上翼面前缘出现明显超声速区，压力分布成尖峰型，前缘附近具有很强的逆压梯度，在低Re数下层流边界层就能很快转变为湍流，其转捩点接近前缘，略靠后于固定转捩位置，激波位置同样略靠后，但差别很小，各个站位压力分布同样差别很小，因而升力系数差别很小，这样就造成自由转捩条件下，升力线在0°发生拐折。

图3 固定转捩和自由转捩计算机翼上翼面层流区范围Fig.3 Comparison of laminar region and turbulentregion between fixed and free transition

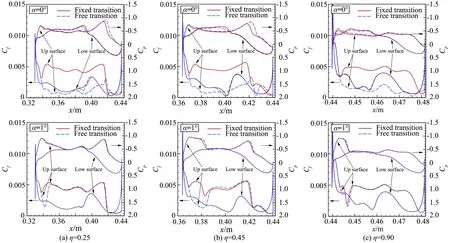
图4 α=0°和1°固定转捩和自由转捩摩阻和压力分布对比曲线Fig.4 Comparison of skin friction and pressure distribution between fixed and free transition

2.3 转捩对超临界机翼边界层流动影响分析

图5分别给出了迎角-2°～1°固定转捩和自由转捩计算机翼上翼面极限流线对比结果。固定转捩时产生湍流边界层/激波相互作用，迎角-2°时固定转捩内翼段后缘有小分离，随迎角增加分离区大小逐渐增加，并向外翼段扩展。自由转捩机翼上翼面流动变化较为复杂，迎角-2°～0°时，激波前为层流区域，产生转捩边界层/激波相互作用，在0°和1°之间，转捩位置突变前移至靠近前缘位置，此时产生湍流边界层/激波相互作用。迎角-2°时，内翼段后缘有小分离，激波强度较固定转捩强而且转捩边界层抵抗激波逆压梯度的能力较弱，从而诱导产生激波后分离气泡，随迎角增加，激波诱导分离气泡和后缘分离弦向范围逐渐增加，至0°时，两者汇合产生激波后缘完全分离。迎角1°时，转捩位置突变前移至机翼前缘附近，湍流边界层承受激波逆压梯度能力较强，激波后分离气泡消失，仅存在后缘分离，此时自由和固定转捩机翼上翼面流动基本相同。

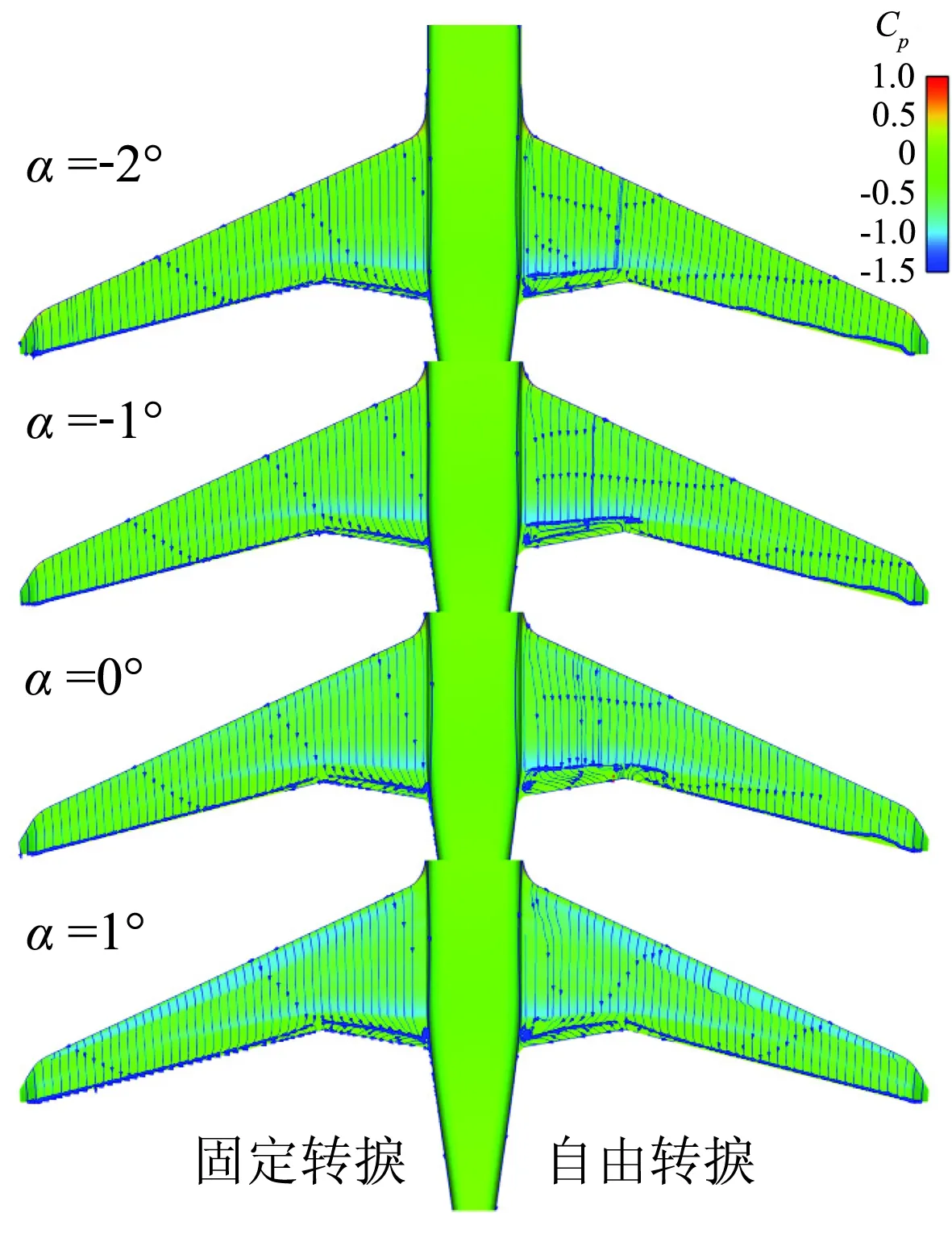
图5 固定和自由转捩计算机翼上翼面极限流线Fig.5 Limited streamline distribution alongthe upper surface of the wing

3 结 论

本文采用RANS方程耦合eN-Database转捩预测方法，研究了转捩对某民机超临界机翼气动特性的影响。与固定转捩相比，自由转捩状态下计算得到的升力系数更大，相同升力系数下计算得到的阻力系数较小，与试验结果趋势一致，进一步验证了本文计算方法的可靠性。对于文中的民机构型，可以得出以下结论：相同迎角下，转捩位置越靠前，激波越靠前，超声速区面积减小，升力随之减小；在迎角0°～1°之间，机翼上翼面自由转捩位置发生急剧移动，是自由转捩升力曲线发生拐折的原因。

参考文献：

[1]Whitcom B, Richard T.Review of NASA supercritical airfoils[R].ICAS Paper No.74-10, 1974.

[2]沈克扬.关于超临界机翼Re数效应的机理研究[J].民用飞机设计研究, 1998, 3: 7-16.

[3]Chen Y C, Si J T, Han X L, et al.Investigation of transition effect on the pressure distribution of super-critical wing[J].Acta Aerodynamica Sinica, 2003, 21(4): 470-475.(in Chinese)陈迎春, 司江涛, 韩先锂, 等.转捩对超临界机翼压力分布的影响分析[J].空气动力学学报, 2003, 21(4): 470-475.

[4]Xu X, Liu D W, Chen D H, et al.Numerical investigation on shock-induced separation structure of supercritical airfoil[J].Advanced Materials Research, 2013, 756-759: 4502-4505.

[5]Wang F, Eriqitai, Wang Q, et al.Boundary layers stability analysis of three typical airfoils[J].Acta Aerodynamica Sinica, 2011, 29(4): 481-485.(in Chinese)王菲, 额日其太, 王强, 等.三种典型翼型边界层稳定性对比分析[J].空气动力学学报, 2011, 29(4): 481-485.

[6]Deng L, Qiao Z D, Yang X D, et al.Computational aerodynamic analysis of thick flatback airfoils coupling RANS and transition prediction code[J].Acta Aerodynamica Sinica, 2011, 29(5): 613-618.(in Chinese)邓磊, 乔志德, 杨旭东, 等.基于N-S方程和自由转捩预测耦合求解的钝后缘翼型气动性能计算[J].空气动力学学报, 2011, 29(5): 613-618.

[7]Huang Z F, Lu X Z, Yu G T.Crossflow instability analysis and transition prediction of airfoil boundary layer[J].Acta Aerodynamica Sinica, 2014, 32(1): 14-20.(in Chinese)黄章峰, 逯学志, 于高通.机翼边界层的横流稳定性分析和转捩预测[J].空气动力学学报, 2014, 32(1): 14-20.

[8]Feng W L, Chen B, Lyu L Y.Research Reynolds number effect correction for air supercritical laminar complex wing[J].Acts Aerodynamica Sinica, 2015, 33(4): 470-474.(in Chinese)冯文梁, 陈斌, 吕凌英.超临界层流复合翼飞机Re数效应修正方法研究[J].空气动力学学报, 2015, 33(4): 470-474.

[9]Muppidi S, Mahesh K.DNS of transition in supersonic boundary layers.AIAA-2011-3564[R].Reston: 2011.

[10]Pan H L, Ma H D, Shen Q.LES application to unsteady flat plate shock wave/turbulent boundary layer interaction[J].Acts Aeronautica et Astronautica Sinica, 2011, 32: 242-248.(in Chinese)潘宏禄, 马汉东, 沈清.基于LES方法的平板非定常激波/湍流边界层干扰研究[J].航空学报, 2011, 32(2): 242-248.(in Chinese)[11]Smith A M O, Gamberoni N.Transition pressure gradient and stability theory[R].Douglas AirCraft Co., CA Rept.ES 26388, Long Beach, CA, 1956.

[12]VanIngen J L.A suggested semi-empirical method for the calculation of the Boundary-Layer transition region[R].Univ.of Delft.Rept.VTH-74, Dept.of Aerospace Engineering, 1956.

[13]Wang G, Liu Y, Wang G Q, et al.Transitional flow simulation based onγ-Reθttransition model[J].Acta Aeronautica et Astronautica Sinica, 2014, 01: 70-79.(in Chinese)王刚, 刘毅, 王光秋, 等.采用γ-Reθt模型的转捩流动计算分析[J].航空学报, 2014, 01: 70-79.

[14]Mend D H, Zhang Y L, Wang G X, et al.Application ofγ-Reθttransition model to two-dimensional low speed flows[J].Acts Aeronautica et Astronautica Sinica, 2011, 32(5): 792-801.(in Chinese)孟德虹, 张玉伦, 王光学, 等.γ-Reθt转捩模型在二维低速问题中的应用[J].航空学报, 2011, 32(5): 792-801.

[15]Jean-Pierre Archambaud, Raffaele Donelli.Automatic transition prediction using simplified methods[C]//47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, 2009.

[16]Cambier L, Heib S, Plot S.ONERA else CFD input from research and feed-back from industry[R].28th International Congress of The aeronautical Sciences, 2012.

[17]Andreas Krumbein.Automatic transition prediction and application to 3D wing configuration [J].Journal of Aircraft, 2007, 44(1): 119-133.

[18]Andreas Krumbein.Automatic transition prediction and application to hight-lift multi-element configurations[J].Journal of Aircraft, 2004, 4(5): 1362-1366.

[19]Normann Krimmelbein, Andreas Krumbein.Automatic transition prediction for three-dimensional configurations with focus on industrial application[C]//40th Fluid Dynamics Conference and Exhibit, 2010.

[20]Zhang K, Song W P.Application of the full eNtransition method to the infinite swept-wing’s transition prediction[J].Journal of Northwestern Polytechnical University, 2011, 01: 142-147.(in Chinese)张坤, 宋文萍.eN方法在无限展长后掠翼边界层转捩判断中的初步应用[J].西北工业大学学报, 2011, 01: 142-147.

[21]Song Wenping, Zhu Zhen, Zhang Kun, et al.Simulations of the viscous flow around swept wings and optimization design using the RANS solver with automatic transition prediction[J].Aeronautical Science & Technology, 2015, 26(11): 23-29.(in Chinese)宋文萍, 朱震, 张坤, 等.耦合转捩自动判断的机翼粘性绕流计算与优化设计[J].航空科学技术, 2015, 26(11): 23-29.

[22]Dong J, Gao D F, Ren Y J, et al.Coupling and appli-cation of eN-database method to transition prediction in a 3D unstructured solver[J].Journal of Shenyang Aerospace University, 2015, 32(2): 11-17.(in Chinese)董军, 高德峰, 任园军, 等.eN-Database转捩预测方法在三维非结构求解器中的耦合与应用[J].沈阳航空航天大学学报, 2015, 32(2): 11-17.

[23]Elsenaar A, Binion TW, Stamewsky E.Reynolds number effects in transonic flows[R].AGARD AG-303, December 1988.