一类级联式双定子无刷双馈发电机静态无功调节能力分析

姜云磊, 程 明, 韩 鹏, 王青松

(东南大学电气工程学院, 江苏省南京市 210096)

0 引言

风力发电是对风能进行大规模捕获、利用的有效途径,至2035年,风力发电有望承担高达35%的新能源供给量[1-2]。成熟的商业化风电场通常按照“分级补偿,就地平衡”的无功补偿方式运作[3],基于这一原则,风电机组应主动参与到电网电压调节之中。风电场的无功补偿既可以通过风力机本身输出无功功率实现,也可以通过投入额外的无功补偿装置,如静止无功补偿器(SVC)、静止同步补偿器(STATCOM)等实现。随着风电机组单机容量和风电场规模的扩大,风电场对电网的影响越来越大。将机组本身作为重要的无功源并充分发掘风电机组自身的无功调节能力,对于降低风电场运营成本并制定相应的无功调节策略显得尤为重要。

在目前主流的风力发电机中,双馈感应发电机(DFIG)以其转差功率变换、功率控制解耦性好的优势得到广泛的研究与应用[4]。然而电刷与集电环的存在降低了机组的可靠性,并且产生了大量的额外维护成本[5],在这一情形下,DFIG的无刷化成为了当今风电领域研究的热点课题[6],出现了多种无刷双馈发电机拓扑结构,按照无刷化的原理可以将主流无刷双馈发电机结构分为两大类:级联式与场调制式。级联式是将有刷双馈发电机与其他电磁设备级联,采用无接触式电能传输的方式实现转差功率在静止电源与转子绕组之间双向流动;调制式则是借助短路绕组、磁阻凸极等手段产生不同极对数的两个旋转磁场并通过转子实现电磁耦合,其详细分类可参阅文献[5]。

目前对基于DFIG的风电场无功运行能力已经有了相对完善的研究成果,但涉及无刷双馈感应发电机(BDFIG)无功调节能力的研究则相对较少。文献[7]对DFIG机组的无功调节范围做了较为完善的考量;文献[8-9]将静态稳定约束条件纳入考虑;文献[10]进一步推导了DFIG主磁通饱和情况下的无功运行范围。关于BDFIG的研究,则主要集中在电机结构设计、电磁分析[11]与高性能控制方法[12],很少涉及并网运行条件下的无功容量计算。本文主要研究无刷双馈发电机在并网条件下的无功调节范围。考虑到机械结构和电气结构的相似性,将视野聚焦到一类双定子无刷双馈发电机(DS-BDFIG),这一类电机本质上属于级联式电机,通过绕线转子实现磁场和功率的间接耦合[13],转子绕组通有电流并处于密闭腔体之内,因而除了受到控制绕组(CW)、功率绕组(PW)电流约束外,其无功调节能力还在很大程度上受到转子绕组电流约束。

本文计及PW、CW和转子绕组电流及网侧变换器(GSC)容量限制,以电机的稳态模型为分析工具并综合考虑了电机运行过程中的铜耗和电感饱和特性,推导了一类DS-BDFIG的无功功率范围,获取了这一类电机在不同工作点下无功运行范围的解析计算方法,以期最大程度地在安全运行范围内发挥DS-BDFIG的无功调节能力。

1 一类具有级联结构的DS-BDFIG

1.1 DS-BDFIG的结构特征

BDFIG最早起源于两台或多台感应电机的级联运行:级联式感应无刷双馈发电机(CBDFIG)通过两台绕线转子感应电机根据如图1(a)所示的同轴级联方式首先实现了无刷化运行。

图1 DS-BDFIG结构Fig.1 DS-BDFIG structure

针对CBDFIG轴向长度长、功率密度低的缺点,文献[14]提出了一种径向布置的新型双定子无刷双馈风力发电机。如图1(b)所示,新型电机结构包含同轴布置的内外两个定子和位于定子之间的杯形转子。定转子上共有4套分布绕组,转子内外层绕组之间反相序相连。这种电机的等效电路与CBDFIG电机类似,但具有更加紧凑的结构、更高的功率密度。然而,双定子结构中,耦合转子内部通常形成一个密闭的腔体,将转子包裹在其中[14],因而耦合转子铜耗和铁耗产生的热量只能通过传导方式经由转轴和端盖散出,内部容易过热。

根据上述分析,当DS-BDFIG参与无功调节时,需要同时考虑流经三套绕组的电流是否超过极限值,同时由于耦合转子散热条件不理想,电流过载倍数低,转子的电流极限势必成为影响机组无功调节能力的重要因素。

1.2 DS-BDFIG的功率关系

基于DS-BDFIG的风力发电系统如图2所示,与DFIG类似,机组PW与电网相连;CW通过一组背靠背变换器实现转差功率的流动;定义Pp和Qp分别为PW侧输出的有功及无功功率;Pc和Qc分别为CW侧输出的有功及无功功率。

若忽略电机各套绕组的损耗,DS-BDFIG机械功率Pmec、PW功率Pp与CW功率Pc的分配关系满足:

Pmec=Pp-Pc

(1)

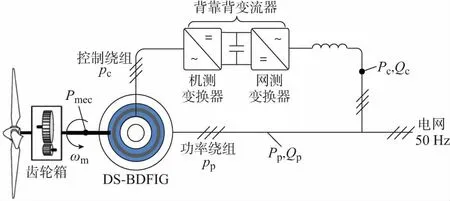
图2 基于DS-BDFIG的风力发电系统Fig.2 Configuration of DS-BDFIG based wind generation system

CW侧有功功率为PW侧有功功率的转差功率,则

(2)

式中:s=ωc/ωp为转差。

Pmech为风力发电机的输入总机械功率,取决于风力机捕获风能的大小，Pmech在功率侧与控制侧之间的分配关系由转差s决定。

1.3 DS-BDFIG的数学模型

为了有效地计算DS-BDFIG的无功容量,首先给出了DS-BDFIG在三相平衡电网情形下的全阶模型如下:

(3)

(4)

式中:ω1=ωp-ppωr，ω2=ωp-(pp+pc)ωr,其中pp和pc分别为电机功率侧和控制侧极对数；ψr为轮子的机械角速度;Ψ,i,u分别为磁链、电流和电压;R,L,ω分别为绕组电阻、自感和角频率;下标p, r, c分别表示与PW、转子绕组和CW相关的参数;Lpr和Lcr分别为PW和CW与转子绕组之间的互感;Rsp和Rsc分别为PW和CW的绕组电阻。

式(3)和式(4)分别描述了DS-BDFIG电压和磁链的动态过程。

2 DS-BDFIG的无功约束条件

2.1 耦合转子电流对PW无功极限的影响

在PW磁链定向的并网工作条件之下,同步旋转坐标系d轴与PW合成磁链矢量相重合;忽略功率侧磁链的暂态过程和PW电阻Rsp的影响,可得

(5)

式中:下标d,q分别表示对应变量的d,q轴分量。

由于PW侧q轴磁链为零,则

(6)

根据式(4)中给出的DS-BDFIG磁链表达式,可以推导出转子电流与PW电流的静态关系如下:

(7)

即

(8)

无刷双馈发电机PW侧无功功率可以在一定范围内进行调节,其调节极限随PW测有功功率变化。按照发电机惯例进行建模,可以得到PW侧有功Pp及无功功率Qp的表达式为:

(9)

将式(8)代入式(9),经整理可以得到PW侧无功功率的约束条件如下:

(10)

在PW有功功率Pp给定的情况下,通过式(10)可以得到PW无功功率的上边界Qpmax,1和下边界Qpmin,1分别为:

(11)

式(11)得出的结果为DS-BDFIG并网条件下第一组无功约束条件,此时无功调节范围主要受到转子绕组热极限电流的约束。

2.2 CW电流约束对PW无功极限的影响

首先将式(8)代入转子绕组磁链表达式中,可以得到:

(12)

同时考虑到闭合转子回路的端电压ur=0,有

(13)

将式(12)代入式(13),消去转子电压方程中的转子磁链,经过整理后可以得到稳态条件下PW电流和CW电流的耦合关系为:

(14)

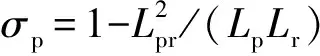
式(14)中的第一项反映了PW和CW电流的直接耦合关系。由于Rr的阻值较小,将其忽略后，式(14)可以近似为:

(15)

进而得到由CW电流决定的无功约束条件如下:

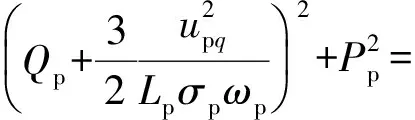
(16)

在PW有功功率Pp给定的情况下,可以得到PW无功功率的上边界Qpmax,2和下边界Qpmin,2分别为:

(17)

式(17)得出的结果为由CW电流约束决定的第二组PW侧无功约束条件。

为了直观说明三种约束条件对无功输出范围的影响,选取一台10 kW DS-BDFIG作为分析对象,结合式(11)和式(17)给出的两组约束条件,绘制出如图3所示的无功输出范围示意图。

图3 10 kW DS-BDFIG无功输出范围示意图Fig.3 Schematic diagram of reactive power output limit for 10 kW DS-BDFIG

2.3 GSC无功功率极限

风力发电系统中,GSC需要为CW提供转差功率,该功率由发电机所处的工作点决定。GSC容量的选取主要基于发电机的最大有功转差功率大小,并考虑一定的机组损耗。设GSC的设计容量为Scmax,那么GSC吸收的无功功率容量为:

(18)

式中:Qg为GSC吸收的无功功率。则GSC的无功极限可以表示为:

(19)

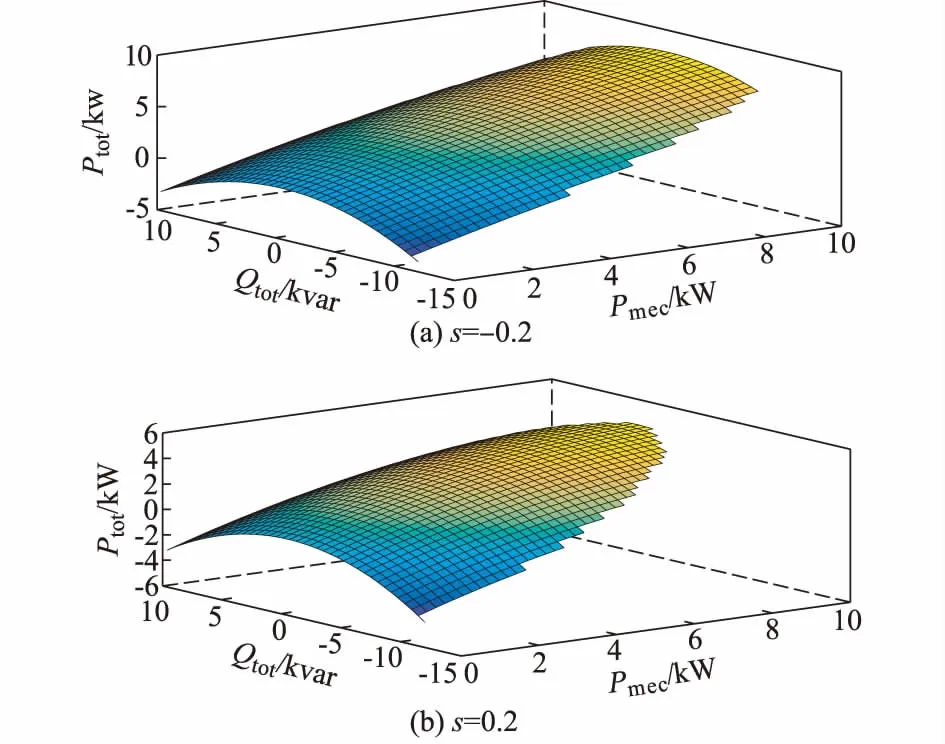
由式(19)可知,当处于亚自然同步速时,0

综合考虑式(18)给出的发电机本身调节容量与式(19)给出的GSC的无功调节能力,可以得到单台DS-BDFIG的无功功率极限为:

(20)

根据式(19),转差s对GSC的无功调节能力同样构成影响。为了更加清晰地获取GSC容量对整套机组无功容量的影响,以机械输入功率Pmec为变量,并仍采用附录A表A1中的电机参数。图4(a)给出了不同转差下机组的无功功率输出范围。图中Qtot为GSC与发电机PW输出无功功率之和。

图4 发电机转差与磁通饱对无功输出的影响Fig.4 Effect of slips and CW saturation on reactive power capability

3 DS-BDFIG机组饱和电感与损耗对无功输出范围的影响

附录A图A1所示为经过绕组归算和频率归算后的DS-BDFIG稳态等效电路,图中上标′和″分别为转子绕组及CW归算到PW侧后的电参数;sp为PW与转子绕组之间的相对转差;sc为转子绕组与CW之间的相对转差,并且sp=scs。考虑到DS-BDFIG中磁路饱和特性,等效电路中CW侧电感使用可变电感替代。

3.1 电感饱和对无功输出范围的影响

当DS-BDFIG并网发电运行时,PW侧电压通常恒定,功率电机工作在恒磁通模式下,而CW工作在变磁通模式下,不同工作点对应不同的励磁电流。

附录A图A2所示为一台DS-BDFIG的PW与CW励磁曲线,励磁曲线的解析表达式由实测数据拟合获取[14],并可被下述两式表达:

(21)

(22)

当励磁电流Imc和Imp增大时,控制电机与功率电机的气隙磁链ψmc和ψmp逐渐饱和。由于受电网电压钳位,PW通常工作于恒磁通模式下,而CW所需励磁电流则随着饱和程度增加而逐渐变大。

图4(b)给出了两种转差下,考虑磁路饱和特性前后机组的有功/无功功率曲线。将CW饱和特性纳入考虑之后,DS-BDFIG的无功范围相比忽略饱和因素时有所降低。这一结果也与从附录A图A1中等效电路获取的直观认识相符:随着电感饱和程度的加深,所需励磁电流增大,机侧变换器(MSC)侧功率因数降低,进而降低PW侧无功容量。

3.2 DS-BDFIG机组铜耗对功率调节能力的影响

图3和图4给出的有功/无功功率曲线,其推导基于式(1)和式(2)所给出的DS-BDFIG理想功率分配关系,事实上机组中铁耗和铜耗的存在直接影响到机组输出有功/无功功率曲线的准确性。

根据现有文献中对DS-BDFIG的损耗分析,铁耗在损耗中并非占主导[15],因而损耗计算中铁耗可被忽略。如电机等效电路所示,DS-BDFIG的铜耗由CW铜耗、PW铜耗和转子绕组铜耗三部分构成,则机组的总损耗可以被表示为:

(23)

式中:Isp,Ir,Isc分别为附录A图A1所示等效电路中流经PW、转子绕组和CW的电流。

式(7)与式(15)给出了磁链定向控制下,PW电流与转子、CW电流的稳态关系,将其代入铜耗计算方程可得:

(24)

式中:Usp为PW端电压。

将式(24)中PW电流使用关于Pp,Qp的表达式替代,可以得到PCu与Pp,Qp的函数关系如下:

(25)

图5分别给出了转差s为-0.2及0.2时,DS-BDFIG机组机械输入功率Pmec、输出有功功率Ptot及输出无功功率Qtot之间的关系。图5在x-o-y平面的投影与图4(a)一致,在考虑机组铜耗的基础上,当输出的机械功率Pmec一定时,DS-BDFIG的有功功率输出随无功输出Qtot的增大而减小,因而,准确的DS-BDFIG有功/无功功率曲线应为图5在y-o-z轴上的一个切面。

图5 不同工作点下DS-BDFIG机组铜耗Fig.5 Copper loss of DS-BDFIG with different active and reactive power

4 计及约束条件的双定子无刷双馈风力发电机无功控制策略

为了有效实现DS-BDFIG机组的无功调节,本节根据上文给出的分析,提供一种计及DS-BDFIG约束条件的MSC的功率控制策略,其简化控制框图如附录A图A3所示。

5 结语

与场调制式BDFG相比,DS-BDFIG在转矩密度和电能质量方面具有明显优势,是一种极有潜力的风力发电机结构。本文以这一类电机为研究对象,从电气和机械结构上的特殊性出发,着重研究了耦合转子、机组损耗与控制侧主电感饱和对无功调节能力的影响,提出了DS-BDFIG无功范围的解析计算方法并得出以下主要结论。

1)对磁链定向控制下稳态关系的分析可知,相比于DFIG和DS-BDFIG机组的无功调节容量除受GSC容量和CW电流约束外,可用无功输出范围更易受到耦合转子电流极限的限制。

2)构建计及损耗的DS-BDFIG机组无功调节能力计算方法,所获结果有利于准确估算特定转差及有功功率输出下机组无功功率的输出范围。

3)DS-BDFIG控制侧主电感则易受饱和程度影响,将这一因素计入考虑后,所获无功调节范围更接近实际运行情况,具有较好的无功容量估算精度。

4)综合考虑上述因素,在电机额定容量近似的情况下,DS-BDFIG的无功调节范围通常小于传统DFIG;而本文提出的DS-BDFIG无功计算方法则可以在已有的约束条件之下,尽可能地在安全运行范围内充分发掘机组的无功补偿能力。

为了简化本文的分析过程,本文的研究对象局限于DS-BDFIG,并主要考虑了电机绕组热约束对无功调节范围的影响,然而,文中所用的解析计算方法在计算精度上有一定的局限性,并且没有考虑到机组的铁耗。今后的工作将主要集中于提高无功范围的解析计算精度,并将研究拓展到场调制型无刷双馈发电机的无功调节机理上。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] CHENG M, ZHU Y. The state of the art of wind energy conversion systems and technologies: a review[J]. Energy Conversion and Management, 2014, 88: 332-347.

[2] 程明,王青松,张建忠.电力弹簧理论分析与控制器设计[J].中国电机工程学报,2015,35(10):2436-2444.

CHENG Ming, WANG Qingsong, ZHANG Jianzhong. Theoretical analysis and controller design of electric springs[J]. Proceedings of the CSEE, 2015, 35(10): 2436-2444.

[3] 王松,李庚银,周明.双馈风力发电机组无功调节机理及无功控制策略[J].中国电机工程学报,2014,34(16):2714-2720.

WANG Song, LI Gengyin, ZHOU Ming. The reactive power adjusting mechanism & control strategy of doubly fed induction generator[J]. Proceedings of the CSEE, 2014, 34(16): 2714-2720.

[4] POLINDER H, FERREIRA J A, JENSEN B B, et al. Trends in wind turbines generator systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2013, 1(3): 174-185.

[5] 程明,韩鹏,魏新迟.无刷双馈风力发电机的设计、分析与控制[J].电工技术学报,2016,31(19):37-53.

CHENG Ming, HAN Peng, WEI Xinchi. Design, analysis and control of brushless doubly-fed generators for wind power application[J].Transactions of China Electrotechnical Society, 2016, 31(19): 37-53.

[6] HAN P, CHENG M, WEI X, et al. Steady-state characteristics of the dual-stator brushless doubly fed induction generator[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 200-210.

[7] 严干贵,王茂春,穆钢,等.双馈异步风力发电机组联网运行建模及其无功静态调节能力研究[J].电工技术学报,2008,23(7):98-104.

YAN Gangui, WANG Maochun, MU Gang, et al. Modeling of grid-connected doubly-fed induction generator for reactive power static regulation capacity study[J]. Transactions of China Electrotechnical Society, 2008, 23(7): 98-104.

[8] 陈宁,王松岩,胡朝燕,等.考虑静态稳定约束的双馈风电机组无功调节容量[J].电力系统自动化,2011,35(24):33-38.

CHEN Ning, WANG Songyan, HU Chaoyan, et al. Reactive power capability of DFIG-based wind power generator considering static stability constraint[J]. Automation of Electric Power Systems, 2011, 35(24): 33-38.

[9] YANG S, WANG W, LIU C, et al. Optimal reactive power dispatch of wind power plant cluster considering static voltage stability for low-carbon power system[J]. Journal of Modern Power Systems and Clean Energy, 2015, 3(1): 114-122.

[10] ENGELHARDT S, ERLICH I, FELTES C, et al. Reactive power capability of wind turbines based on doubly fed induction generators[J]. IEEE Transactions on Energy Conversion, 2011, 26(1): 364-372.

[11] HESIEH M F, CHNAG Y H, DORRELL D G. Design and analysis of brushless doubly fed reluctance machine for renewable energy applications[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-5.

[12] WEI X, CHENG M, WANG W, et al. Direct voltage control of dual-stator brushless doubly-fed induction generator for stand-alone wind energy conversion systems[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-4.

[13] PENG H, CHENG M, WEI X, et al. Modeling and performance analysis of a dual-stator brushless doubly fed induction machine based on spiral vector theory[J]. IEEE Transactions on Industry Applications, 2016, 52(2): 1380-1389.

[14] PENG H, CHENG M, LUO R. Design and analysis of a brushless doubly-fed induction machine with dual-stator structure[J]. IEEE Transactions Energy Conversion, 2016, 31(3): 1132-1141.

[15] PENG H, CHENG M, JIANG Y. Torque/power density optimization of a dual-stator brushless doubly-fed induction generator for wind power application[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9864-9875.

[16] 胡家兵,贺益康,郭晓明,等.不平衡电压下双馈异步风力发电系统的建模与控制[J].电力系统自动化,2007,31(14):47-56.

HU Jiabing, HE Yikang, GUO Xiaoming, et al. Modeling and control of the DFIG based wind power generation system under unbalanced grid voltage conditions[J]. Automation of Electric Power Systems, 2007, 31(14): 47-56.

[17] SHAO S, ABDI E, BARATI F, et al. Stator-flux oriented vector control for brushless doubly fed induction generator[J]. IEEE Transactions on Industrial Electronics, 2009, 56(10): 4220-4228.