考虑风速分区的风—储系统短期频率响应协同控制策略

彭 勃, 张 峰， 梁 军

(电网智能化调度与控制教育部重点实验室(山东大学), 山东省济南市 250061)

0 引言

随着风电并网容量的逐年增加,风电所具有的间歇性与随机性等特点给电力系统带来了新的挑战[1-2]。其中双馈感应风电机组(doubly-fed induction generator (DFIG) based wind turbine)是目前风电场应用最为广泛的变速恒频风电机组。该类风电机组通过电力电子变流器变速恒频运行输出有功功率,但风电机组转子并不与电网直接相连[3-5],因此,风力机缺乏转子惯量,机组转速与电网频率解耦[6-7],不具备同步发电机组的频率响应能力。在风电机组高比例接入的区域电网中,大量风电机组对传统机组的替代会使该区域电网的总惯量降低[8-9]。因此,使风电机组具备包含惯性响应与一次调频的短期频率响应能力,对高风电渗透率地区电网的频率稳定性以及电网的安全稳定运行都具有重要意义。

针对这一问题,国内外已有一系列相关研究成果。其中,附加惯性控制环节[4-5,7-10]的方法经常被应用于此类研究。该方法以系统频率作为输入信号,经微分控制环节,将附加控制信号叠加在风力机的最大功率点跟踪(maximum power point tracking,MPPT)环节之上,实现变速风电机组的虚拟惯性频率响应,然而风力机所能提供的虚拟惯性响应能力与其响应前运行状态直接相关,风速的随机性与波动性难以保证风电机组具有持久可靠的惯性响应能力,而且易造成系统频率的二次波动,不利于系统频率稳定;转速控制[10-12]、桨距角控制[13-14]与综合控制[15-16]等方法通过降低风力机的风能捕获效率,使风力机工作在减载运行状态,以留出为应对系统频率波动而提供短期功率支持的备用容量,然而长期的减载运行会使风电机组经济效益受到较大影响。

近年来,储能由于其性能稳定、控制灵活、响应快速等特点[17]被广泛应用于平抑可再生能源出力波动[18]、调峰调频[19]等场合,适合应用于系统的短期频率调节场合。文献[15,20]中风力机通过减载运行来维持一定的调频备用容量,并应用储能装置来弥补风力机备用容量不足以应对频率波动的场合,此时风力机仍然需要长期运行在减载状态以留有备用容量,牺牲了风力机的最大风能捕获效率。文献[21]提出了利用储能装置来补偿风电机组惯量的控制策略。该控制策略虽然能够提高风电机组的惯性频率响应能力,但储能承担了全部的频率响应需求,导致储能容量需求偏高。鉴于目前储能成本仍然较高,单纯依靠储能来补偿风电机组惯量的经济性有待验证。文献[19]从风—储配合的角度探讨风电机组的短期频率响应能力,虽然所提控制策略可以使风电机组在日常以MPPT模式运行,储能只在辅助风力机转速恢复过程中起作用,但没有考虑不同风速下风力机调频能力的差异以及变风速下的应对策略。上述研究所提出的控制策略虽然都在一定程度上增加了风电机组的惯量,使其具备了短期频率响应能力,但所提出的控制策略中风力机转子动能缺乏与储能的有效协同配合,而且风—储系统不但无法满足多风况下的系统调频需求,还造成了风电机组运行效益的降低以及储能的高成本配置需求。

为应对上述问题,本文将同步发电机组的惯性频率响应以及一次调频阶段整合为短期频率响应阶段,提出了考虑风速分区的风—储系统短期频率响应协同控制策略。该控制策略将风速详细分区,通过模糊逻辑控制器实现了二者的协同配合,增加了风—储系统的惯量,使其具备了短期频率响应能力,改善了系统的频率稳定性。

1 风—储系统虚拟惯量及短期频率响应能力

电力系统中的同步发电机组用于短期频率响应的能量主要来源于储存在其转子中的旋转动能Ek,SG[6,22],可表示为:

(1)

式中:J为同步发电机组的转动惯量;ωm为同步发电机组的转子角速度。

通常,惯性时间常数H被用来表示同步发电机组惯量的大小,其被定义为同步电角速度ωs下的发电组转子动能与发电机组额定容量SN之比,即

(2)

定义风—储系统的虚拟惯性时间常数为Hvir,可表示为:

(3)

式中:Ek,DFIG,j为第j台双馈感应风电机组的转子旋转动能;EESS为储能系统响应系统频率波动而输出的电能;SDFIG,ES为风—储系统的总额定容量。

当系统频率波动时,风—储系统用于提高等效惯性频率响应能力的有功功率变化量ΔP可表示为:

(4)

式中:ΔPDFIG和ΔPESS分别为双馈感应风电机组与储能系统的有功功率输出变化量;Jvir为风—储系统虚拟同步发电机组的虚拟转动惯量;ωv为风—储系统的虚拟同步发电机组转子角速度。

将式(3)代入(4)得到:

(5)

并将式(5)转换为标幺值形式如下所示:

(6)

ΔE*=Hvir[(f*(t+Δt))2-(f*(t))2]

(7)

式中:ΔE*为风—储系统进行惯性频率响应的电能标幺值。

式(7)可整理为:

(8)

由式(8)可知,风—储系统可以通过输出有功功率来响应系统频率波动;对于一定的ΔE*,风—储系统的虚拟惯性时间常数越大,则系统的频率波动越小。

电力系统的频率响应可以分为惯性响应、一次调频与二次调频或自动发电控制(automatic generation control,AGC)这3个阶段[4],由于风力机转子中所储存的转子动能有限,以及储能较为昂贵的容量配置成本,因此二者都无法在较长时间尺度上参与系统的频率调节。相比之下,在频率发生波动后的惯性响应阶段与较短时间尺度的一次调频阶段,更加适合通过风力机与储能系统的协同配合来提升系统惯量,抑制系统频率波动。本文将风—储系统应对系统频率波动的惯性响应以及之后的一次调频时间段内的频率响应归为短期频率响应,本文的控制策略也主要应用于频率发生波动后的这段时间之内。

2 基于模糊逻辑与风速分区的风—储系统协同控制策略设计与实现

模糊逻辑控制无需对被控过程进行定量的数学建模,当被控过程十分复杂或者被控过程的数学模型难以准确建立时,模糊逻辑控制就显得更具实用性[23]。在风—储系统中,依据当前频率特性以及风力机运行状态来决定风—储系统响应系统调频需求的有功功率增量是一个非常复杂的过程,其数学模型难以准确建立,故模糊逻辑控制方法对此过程十分适用。

为使所提控制策略能够适应多种风况,需要将不同风速下风电机组的转速—功率特性进行分区归类,再以此为基础制定适应各风速区段特点的运行控制策略。

2.1 风速分区方法

风力机正常运行时,采用MPPT运行模式来捕获当前风速下的最大风功率。风力机出力与当前风速直接相关,不同的风速对应着各自的最大风功率与最优转速,因此,若利用风力机的转子动能参与频率调节,则需要了解当前风速所对应的风力机出力以及风力机转子转速。

为方便制定不同风速下风—储系统响应系统调频需求的运行控制策略,将1.5 MW双馈风电机组在不同风速下的最优功率、转子转速分为4个区间(见附录A图A1)。将风速小于6 m/s的区间划分为风速一区,此区间风力机转子转速ωr仅能保持最低转速ωr,min,无法通过降低转速释放旋转动能的方式响应调频需求;将6～11 m/s的风速区间划分为风速二区,此区间风力机转子转速为最优转速以保持MPPT运行模式来捕获当前风速下的最大风功率;将11～12 m/s的风速区间划分为风速三区,此区间风力机转子转速达到上限值并被维持在转速上限ωr,max,同时风力机出力Pw接近额定值PN;将风速大于12 m/s的区间划分为风速四区,此区间风力机出力达到额定值PN,此时控制系统通过增大桨距角将风力机输出功率维持在风力机出力额定值。

由于风速一区中风力机转子动能不足,风速区间四区中风力机输出功率达到额定值无法越限增发,因此,当风速处于此两区间时,风力机往往无法参与调频,限制了风电场响应系统调频需求的风速区间宽度,无法在跨度较大的风速区间都能够参与频率调节。

本文提出的基于模糊逻辑控制的风—储系统协同控制策略以风速分区为基础,针对各风速区间特点制定相应的运行控制策略,使风—储系统具备在风速一区至风速四区均能响应系统短期频率调节需求的能力。

2.2 模糊逻辑控制方法

在附录A图A1风速分区的基础上,本文通过模糊逻辑控制方法实现了风力机与储能系统的灵活配合,以提高风—储系统的短期频率响应能力。

风—储系统协同控制策略中的模糊逻辑控制器共有2个。其中,第1个模糊逻辑控制器(FLC1)用于决定风—储系统惯性频率响应的总有功功率增量;第2个模糊逻辑控制器(FLC2)用于决定风力机的调频参与系数,即风力机在惯性频率响应中有功出力的大小。因此,FLC1与FLC2共同决定了风—储系统中储能系统所需承担的调频需求,在整个短期频率响应的过程中,储能系统都在与风力机灵活配合,在充分利用风力机调频潜力的同时还避免了风力机过度参与调频,从而实现了风—储系统协调配合运行。

不同于传统同步发电机组在惯性频率响应阶段有转子旋转动能阻尼,以及一次调频阶段有调速器,风力机本身不具备惯性响应能力和一次调频能力,在风力机的短期频率响应实现过程中,这2部分没有明确的阶段分界,都体现为风力机释放转子动能以及储能系统的有功功率。从短期频率响应启动的条件来说,若系统频率偏差Δf的绝对值或系统频率变化率df/dt的绝对值超过设定值,则频率响应标志位都会启动来触发短期频率响应,风—储系统短期频率响应的有功出力大小则由模糊逻辑控制器决定。

对于FLC1,其输入与输出变量对应关系及隶属函数曲线如附录A图A2所示,其输入为Δf(-1～0 Hz)与df/dt(-0.6～0.6 Hz/s)[21],输出为风—储系统的惯性响应总支持有功功率增量ΔPtotal,SPT(0～0.25(标幺值))。FLC1根据系统频率的变化情况实时决定风—储系统的短期频率响应总有功功率增量,动态模拟了同步发电机组的惯性响应特性,补偿了风—储系统的频率响应惯量。FLC1的模糊逻辑推理表如附录A表A1所示。其建立原则为:当Δf较大或者df/dt绝对值较大时,则输出ΔPtotal,SPT较大;当Δf较小并且df/dt接近于0时,则输出ΔPtotal,SPT较小,因此有利于系统频率稳定。

对于FLC2(见附录A图A3),其输入为风速二区、三区的风力机转子转速ωr(0.7～1.2(标幺值))以及此风速分区的风力机出力参考值Pw,ref(0.2～1(标幺值)),输出为风力机的短期频率响应参与系数α(0～1(标幺值))。FLC2根据当前风速下风力机参与惯性响应的能力来决定α,进而决定了风—储系统短期频率响应过程中风力机所承担的出力增量,如下式所示:

ΔPw,SPT=αΔPtotal,SPT

(9)

式中:ΔPw,SPT为风力机短期频率响应有功功率增量。

此时储能系统短期频率响应有功功率增量ΔPess,SPT如下式所示:

ΔPess,SPT=(1-α)ΔPtotal,SPT

(10)

其模糊语言变量含义可参考FLC1中的定义。根据风力机功率和转速曲线及风速分区,推理表的建立原则为:当ωr较大且Pw,ref较大时,则输出α较大;当ωr非常小时则输出α尽可能小;当Pw,ref非常大时,则输出α尽可能小。FLC2的模糊逻辑推理表见附录A表A2。

通过在风—储系统中引入模糊逻辑控制器FLC1与FLC2,使风力机可以根据实时频率偏差与变化率,以及自身当前状态,动态决定参与频率调节的程度。在充分利用了风力机转子旋转动能调频潜力的同时还避免了风力机对调频需求的过度要求。同时,由于系统总的调频出力增量由FLC1实时决定,故风—储系统中储能系统所需承担的调频需求也随之确定,储能系统可灵活配合风力机,实现风—储系统协调配合运行。

2.3 风力机运行控制策略的实现

基于2.2节中模糊逻辑控制器FLC2的输出,风力机的调频参与程度即可确定。本节进一步确定风力机的运行控制策略。通过对风力机的控制,风力机可以释放转子动能响应系统频率调节需求。本文所用双馈风电机组模型的控制原理图见附录A图A4,其控制运行原理可参见附录A中介绍。

双馈风电机组的控制框图如图1所示,其中,TG为风力机转子侧变流器时间常数;Pe与Pm分别为风力机的电磁功率与风能输入的机械功率;β为桨距角;Hw为风力机自身的惯性时间常数;Tcmd为转矩控制信号；Pcmd为转矩控制下的输出功率指令;PI为比例—积分控制器。以系统频率下降为例,此时转子转速随着转子动能的释放而逐步下降;当系统频率恢复到正常范围后,转子转速也会逐渐恢复,因此双馈风电机组的频率响应控制主要包含系统频率检测、频率支持以及转速恢复等3个环节。

图1 双馈风电机组控制框图Fig.1 Control block of DFIG based wind turbine

对于频率检测环节,通过实时测量系统频率,与系统额定值[21]进行比较,当系统频率偏移或频率变化率检测结果的绝对值超出允许值则将控制系统的频率响应标志位置1,此时风—储系统进入短期频率响应阶段。

当频率响应标志位为1时,进入频率支持环节。模糊逻辑控制器FLC2以当前风力机转子转速ωr与出力参考值Pw,ref作为输入变量,经过模糊规则,可以得到风力机的参与系数α,由此得到短期频率响应有功功率增量ΔPw,SPT,此时风力机退出MPPT运行模式,并将当前转速参考值ωr,ref设置为追踪因释放旋转动能而下降的当前转子转速ωr,随风力机出力增加转速下降,从而实现风电机组的惯性频率响应。

在转速恢复环节,当风力机的频率控制结束时,频率响应标志位置0,风力机重新以MPPT模式运行,此时风力机转子转速参考值设置为附录A图A1中的当前风速下的最优转子转速,之后在风力机的转矩控制下逐步恢复风力机的转速。

通过以上运行控制策略,风力机能够通过释放转子动能响应系统频率调节需求,充分发挥转子的旋转动能的调频潜力,并通过FLC2动态决定参与系统频率调节的程度。

2.4 储能系统运行控制策略的实现

利用2.2节中模糊逻辑控制器FLC1与FLC2的输出,储能系统参与调频的有功功率即可确定。本节进一步确定储能系统的运行控制策略。本文所用储能系统模型为MATLAB/Simulink原件库中的电池模组,其等效电路图及运行原理见附录A图A5及相关介绍。

储能系统在风—储系统中的主要作用是与风力机协同配合进行有功功率支持以应对系统频率波动和增加风电机组的惯量,并使之具备短期频率响应能力以及辅助风力机恢复转速,从而避免频率的二次跌落。在整个风—储系统的短期频率响应的过程中,储能系统都能与风力机进行动态配合。

当风速处于二区与三区且风力机转子转速大于最低转速,此时风力机具备利用转子动能响应频率波动的能力,储能系统则配合风力机响应频率波动。如图2所示,Pess为当前储能系统输出有功功率;储能系统参与频率响应的有功功率增量ΔPess,SPT为FLC1的输出ΔPtotal,SPT与FLC2的输出ΔPw,SPT之差;fref为系统频率参考值;f为系统频率。

当风力机退出调频进入转速恢复阶段,风力机出力骤降,此时储能系统增大有功功率输出以弥补风力机出力的缺失所造成的功率不平衡,减小风力机出力骤降造成频率二次跌落的影响。

当风速处于一区与四区时,风力机由于其转速与功率限制无法利用转子动能参与调频,因此储能系统单独响应这2个区段时的频率波动,使风—储系统具备适应更宽风速范围的系统频率调节响应能力。然而,为了避免系统频率恢复过程中储能系统功率的过度释放,在控制环节中附加了储能系统功率的下垂环节,当系统频率回升达到49.8 Hz[24]时,储能系统的输出功率将逐渐变缓,经下垂环节修正后的储能系统参与频率响应的有功功率为Pess,drop,如下式所示:

(11)

式中:Pess,49.8为频率为49.8 Hz时储能系统的有功功率。

图2 储能系统控制框图Fig.2 Control block of energy storage system

为弥补当储能结束响应频率波动时所引起的冲击以及最终将频率稳定在设定频率,在储能系统控制框图中附加了PI环节。当系统实测频率大于49.8 Hz时此环节启用,综上,储能系统参与频率响应的有功功率输出Pess,SPT如下式所示:

(12)

式中:ΔPPI为图2中PI调节的输出,即储能系统有功功率输出的修正量。

通过以上储能控制环节以及模糊逻辑控制器的共同作用,实现了以有限容量的储能设备与风力机相配合,在使风—储系统具备在多种风况下响应系统频率调节需求能力的同时,避免了在风力机结束或退出调频时,输出功率的瞬间下降所造成的系统频率二次跌落问题。

2.5 储能系统的有功功率与容量需求分析

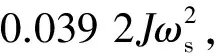
(13)

设储能系统在时间间隔Δt内释放出的能量与同步发电机组动能相同,即

Pess,nΔt=0.078 4PNH

(14)

式中:Pess,n为储能系统的额定功率。

一般发电机组惯性时间常数H约为5 s,设Δt≈2H,则Pess,n可表示为:

Pess,n≈0.04PN

(15)

故在本文控制策略下,本文选取4%PN作为储能系统的额定功率Pess,n。由于储能系统用于配合风力机进行短期频率响应,故储能系统的持续充放电时间仅需数十秒至数分钟即可满足要求,本文取4 min作为储能系统持续充放电的时间长度,以此可得其能量容量。

设储能系统使用寿命为20年,在此时间尺度上,本文所提出风—储系统协同控制策略下的储能系统配置成本与仅有风力机长期留备用模式[15]产生的机会成本,以及储能系统单独进行频率响应[21]的配置成本对比见附录A中表A3与表A4。通过对比可知,本文所提控制策略的成本低于另外2种控制策略,故本文所提控制策略具有经济可行性。

2.6 风—储系统协同控制流程

以风速分区为基础,采用不同的风—储系统协同配合控制策略。基于模糊逻辑控制的风—储系统协同控制策略总体流程图如图3所示。

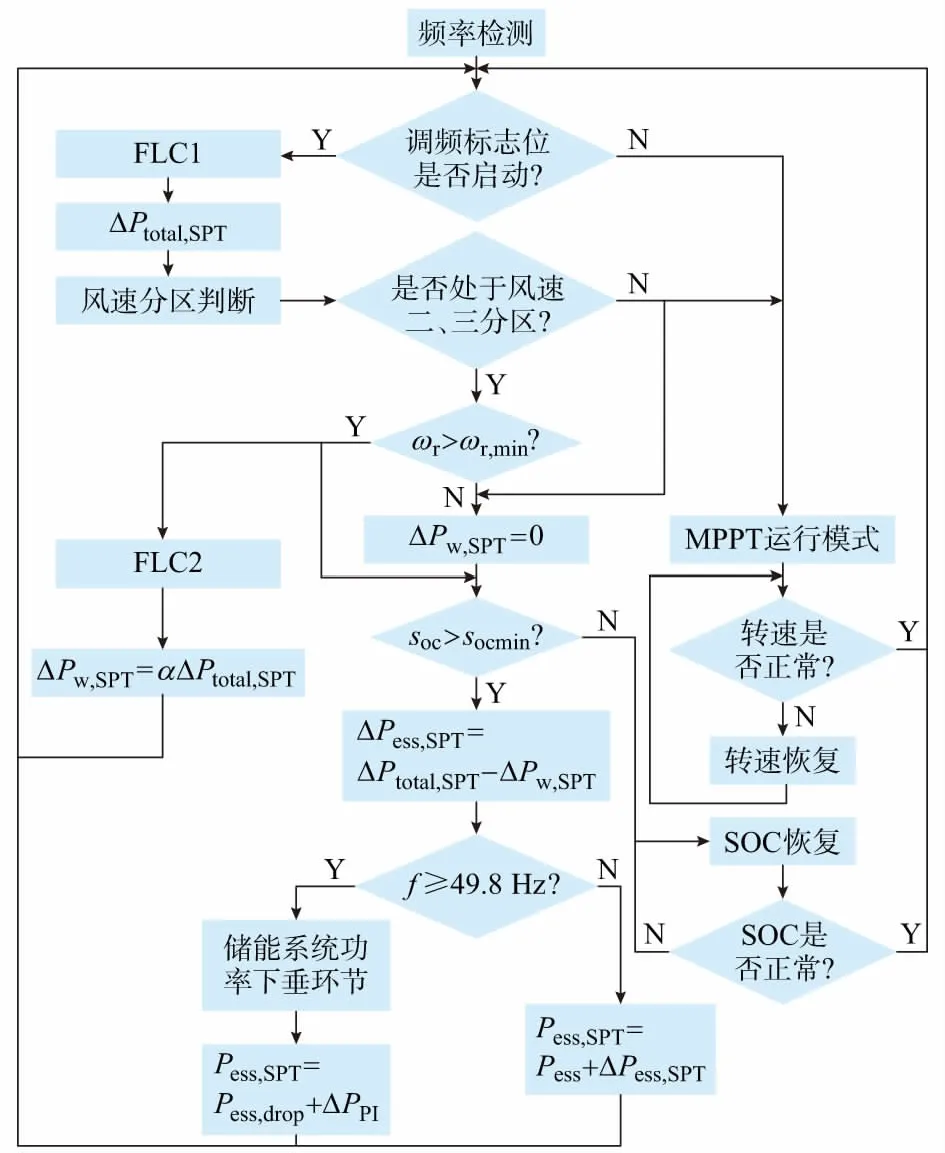
图3 风-储系统协同控制流程图Fig.3 Flow chart of coordinated control strategy of wind-energy storage system

1)当系统频率偏移检测结果的绝对值超出允许值0.033 Hz时,频率响应标志位启动,进入风速分区判断环节,否则风力机以MPPT模式正常运行。

2)若当前风速处于风速一区,此时仅能通过储能系统响应系统频率波动。当储能系统荷电状态(state of charge,SOC)soc大于下限值socmin,则系统通过模糊逻辑控制器来决定输出有功功率的大小,否则进入SOC恢复环节。

3)若当前风速处于风速二区,风力机转子转速大于ωr,min时,由FLC2得出风力机的调频参与系数来决定风力机的频率响应功率增量ΔPw,SPT;当风力机转速下降到小于ωr,min或者频率上升速率高于0.2 Hz/s时,风力机终止惯性频率响应,启动转速恢复环节;风力机退出后,由储能系统弥补风力机退出调频所形成的功率缺额并继续支持系统频率恢复。

4)若当前风速处于风速三区,此区段的运行控制策略与风速处于风速二区中大致相同,但此区间风力机出力较高,在释放转子动能增加出力的同时不能超过风力机的出力上限。

5)当风速处于风速四区时,此时风力机出力达到额定值,并保持MPPT模式不变,储能系统则承担此区段的调频任务,并通过SOC判断是否进入SOC恢复环节。

3 仿真验证

3.1 仿真系统介绍

为了验证本文所提控制策略的有效性,在MATLAB/Simulink平台上搭建仿真系统。由于本文基于单台双馈风电机组对应单台储能装置的控制策略具有普适性,故在仿真系统中选取一个等值双馈风电机组代表风电场。仿真系统包括与等值风电机组对应的储能系统、3台同步发电机组、变压器、负荷以及等值线路组成。仿真系统结构图与详细参数见附录B图B1、表B1至表B4。

对于频率偏高事件,通过调节风力机转子转速或者桨距角使风力机运行在非MPPT模式,在各风速区间内运行的风力机都可以实现减载,从而对频率升高事件做出响应。相较于根据当前风力机运行状态释放转子动能增加风力机的出力而言,降低风力机出力更易实现。在应对频率偏高事件时,风力机与储能系统的协同配合过程与应对频率跌落时十分相似,区别在于风力机减载无法满足的调频需求需要通过储能系统从电网充电来进行,之后再通过转子转速与桨距角控制使风力机恢复MPPT运行状态。因此,本文主要针对电网频率跌落事件进行仿真与分析。在5 s时,设置负荷功率突增50 MW。

3.2 不同风速下的仿真结果

本文对所提出的风—储系统协同控制策略、仅有风力机附加惯性环节的控制方法[5]以及无附加控制的情况进行仿真,通过对比这3种控制方式的仿真结果来验证风—储系统协同控制策略的有效性以及与传统的风力机惯性控制方法相比的优越性。此3种控制方法在仿真结果图中分别以风—储协同控制、附加惯性控制以及无控制表示。

本文选取系统运行在风速二区和风速四区来检验本文控制策略的应用效果。由于当风速处于风速一区与风速四区时,利用储能系统来满足系统频率响应需求,所提出控制策略对于二者的处理流程类似,故这里仅分析风速在风速四区时的情况。风速三区的仿真结果可见附录B图B2。

1)系统运行在风速二区的仿真结果

取仿真风速为9 m/s。如附录A图A1所示,此时风速位于风速二区。在风力机转速不低于下限的前提下,充分利用风力机转子动能响应频率波动,并利用储能系统作为风力机参与调频的补充是本文控制策略在此区段的控制目标。

图4为仿真系统运行在风速二区时的仿真结果。其中,图4(a)为系统频率响应曲线,风—储系统协同控制策略下的系统频率最低值fnadir为49.4 Hz,高于另外2种控制方式,有效提升了频率下跌最低值。图4(a)中在仅有风力机参与调频的控制方式下,当风力机退出调频时,其输出功率将快速降低,随之导致系统频率的二次跌落,不利于系统频率稳定。图4(b)与图4(c)分别为风速二区中风电机组出力曲线和风力机转子转速曲线,相比于仅有风力机的控制方式,风—储系统协同控制策略下的风电机组出力由模糊逻辑控制器得出风力机参与系数与风电机组总支持有功功率值来决定。处于风速二区时,风力机调频参与系数受转速影响,随着风力机转子转速降低而逐渐减小,风力机所分担的调频功率需求也逐渐减小,直至达到退出条件而退出调频。无控制方式下风力机出力一直保持MPPT模式运行,无法响应系统频率波动。在仅有风力机附加惯性环节的调频方式下,风力机承担更多的出力,需释放更多的转子动能使得转速下降更多,调频结束后恢复至MPPT模式更慢。储能系统有功功率输出如图4(d)所示,在风—储系统投入调频初期,风力机参与系数较高,故此时储能系统所承担的有功功率较小,主要功能是弥补风力机承担调频出力的不足;当风力机在14.9 s退出调频后,为抑制风力机出力骤降造成系统频率二次跌落,储能系统通过增发功率来弥补风力机功率缺额,并辅助风力机转速恢复。

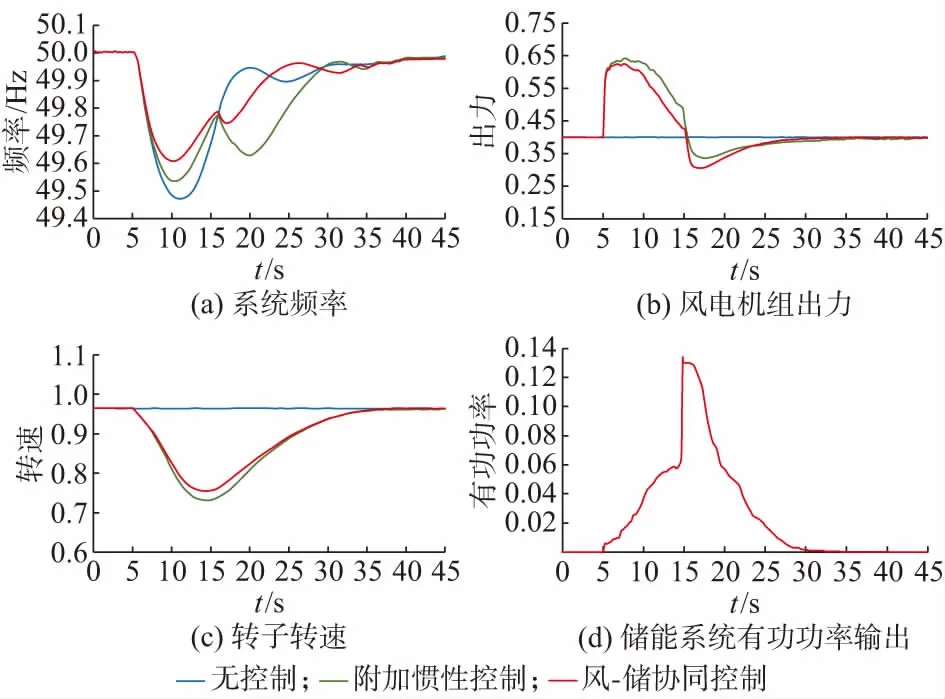
图4 系统处于风速二区时仿真结果Fig.4 Simulation results of power systems when operating in the second wind speed section

通过将本文所提控制策略在此风速区段的控制效果与其他控制方式对比,可以看出本文控制策略能够满足系统在风速二区运行时的频率调节需求,当系统频率发生波动时,能更加有效地提升系统惯性,抑制了频率的下跌速率,使系统频率下跌的最低点升高;通过储能系统与风力机的配合,抑制了频率的二次跌落,提升了此风速区段内风—储系统的短期频率响应能力。

2)系统运行在风速四区的仿真结果

当风速达到12 m/s以上时,即进入风速四区,此时,风力机无法单独参与调频,本文利用储能系统的有功功率输出来响应此风速区段的频率波动,使风电场在高风速下也具备短期频率响应能力。

图5对比了在风速四区,系统在不同控制方式下发生负荷突增后的系统频率曲线。在仅有风力机附加惯性环节参与调频的控制方式下，由于风力机的出力达到上限时无法参与调频,故本文控制策略仅与无控制时的情况进行对比。如图5(a)所示,风—储系统此时仅储能系统输出有功功率,此控制方式下系统频率最低点较无控制方式有较明显上升;由于此风速区段风电机组出力达到最大值,在正常情况下风电机组出力占系统出力比例较大,系统惯量相对较低,当发生相同程度的负荷波动时,系统频率波动幅度相较于风速二区与风速三区时更大,故在风速四区时系统频率跌落最低点低于前2个风速区段。图5(b)为储能系统有功功率输出曲线,当系统频率回升超过49.8 Hz后,为了储能系统有功功率输出不至于过大而影响系统频率稳定性,储能系统下垂环节投入,使储能系统有功功率输出平稳降低;系统频率超过49.9 Hz后,PI环节投入,在储能系统有功功率输出上增加修正量,使系统频率稳定在额定值附近。

图5 系统运行在风速四区时仿真结果Fig.5 Simulation results of power system when operating in the fourth wind speed section

此算例验证了本文控制策略在风—储系统运行在风速四区时,通过对储能系统的充分利用,满足了系统频率调节需求,有效抑制了系统频率波动,弥补了此风速区段仅风力机参与调频时由于出力达到上限而无法应对的不足。

4 结语

本文针对双馈感应风电机组不具备短期频率响应能力的问题,将不同风速下的风力机转速—功率特性分区细化,提出了基于模糊逻辑控制与风速分区的风—储系统短期频率响应协同控制策略。通过仿真,与仅应用附加惯性环节等方法进行了对比,结果表明,本文所提出风—储系统协同运行控制策略能够充分利用风力机与储能系统的调频潜力,将二者协同配合,不仅能够适应多种风况,还避免了风力机退出调频造成的系统频率的二次跌落问题,有效提升了风—储系统的短期频率响应能力。

本文的研究重点在于不同风速区间下单台风力机与单套储能系统配合进行短期频率响应的控制策略并验证其可行性。在高风电渗透率电力系统中,风电场中的机组分布较为广泛,往往处于不同的运行状态,以本文的研究为基础,对于含多种不同运行状态风力机的风电场,FLC1可用于得出当前频率事件下风电场的频率响应功率需求;基于风速分区,对风电场内各风力机运行状态进行评估,可以统计出风电场中具备参与频率响应能力的风力机;此时,各风力机的FLC2再根据当前风力机运行状态决策出各自的频率响应参与系数,以此为参考,从风电场的角度将频率响应的功率需求在有调频能力的风力机与储能系统之间进行合理分配,从而实现储能系统与同一风电场内多台不同运行状态的风力机配合参与频率响应的目的。然而,风电场中不同风力机的运行状态信号的协调管理与频率响应能力的评估,以及风电场对调频需求的合理分配问题仍然需要进一步研究,这将作为本文下一步的研究方向。

本文得到山东大学青年学者未来计划资助,特此致谢！

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[2] 唐西胜,苗福丰,齐智平,等.风力发电的调频技术研究综述[J].中国电机工程学报,2014,34(25):4304-4314.

TANG Xisheng, MIAO Fufeng, QI Zhiping, et al. Survey on frequency control of wind power[J]. Proceedings of the CSEE, 2014, 34(25): 4304-4314.

[3] TENG Fei, STRBAC G. Assessment of the role and value of frequency response support from wind plants[J]. IEEE Transactions on Sustainable Energy, 2016, 7(2): 586-595.

[4] OCHOA D, MARTINEZ S. Fast-frequency response provided by DFIG-wind turbines and its impact on the grid[J]. IEEE Transactions on Power Systems, 2017, 32(5): 4002-4011.

[5] WANG Shuo, HU Jiabing, YUAN Xiaoming, et al. On inertial dynamics of virtual-synchronous-controlled DFIG-based wind turbines[J]. IEEE Transactions on Energy Conversion, 2015, 30(4): 1691-1702.

[6] 李世春,邓长虹,龙志君,等.风电场等效虚拟惯性时间常数计算[J].电力系统自动化,2016,40(7):22-29.DOI:10.7500/AEPS20150527014.

LI Shichun, DENG Changhong, LONG Zhijun, et al. Calculation of equivalent virtual inertial time constant of wind farm[J]. Automation of Electric Power Systems, 2016, 40(7): 22-29. DOI: 10.7500/AEPS20150527014.

[7] WILCHES-BERNAL F, CHOW J H, SANCHEZ-GASCA J J. A fundamental study of applying wind turbines for power system frequency control[J]. IEEE Transactions on Power Systems, 2016, 31(2): 1496-1505.

[8] 李世春,邓长虹,龙志君,等.适应于电网高风电渗透率下的双馈风电机组惯性控制方法[J].电力系统自动化,2016,40(1):33-38.DOI:10.7500/AEPS20150329002.

LI Shichun, DENG Changhong, LONG Zhijun, et al. An inertial control method of doubly fed induction generators suitable for power grid with high wind power penetration[J]. Automation of Electric Power Systems, 2016, 40(1): 33-38. DOI: 10.7500/AEPS20150329002.

[9] 朱晓荣,蔡杰,王毅,等.风储直流微网虚拟惯性控制技术[J].中国电机工程学报,2016,36(1):49-58.

ZHU Xiaorong, CAI Jie, WANG Yi, et al. Virtual inertia control of wind-battery-based DC micro-grid[J]. Proceedings of the CSEE, 2016, 36(1): 49-58.

[10] HU Jiabing, LI Sun,YUAN Xiaoming, et al. Modeling of type 3 wind turbines with df/dtinertia control for system frequency response study[J]. IEEE Transactions on Power Systems, 2017, 32(4): 2799-2809.

[11] 赵晶晶,吕雪,符杨,等.基于可变系数的双馈风机虚拟惯量与超速控制协调的风光柴微电网频率调节技术[J].电工技术学报,2015,30(5):59-68.

ZHAO Jingjing, LÜ Xue, FU Yang, et al. Frequency regulation of the wind/photovoltaic/diesel microgrid based on DFIG cooperation strategy with variable coefficients between virtual inertia and over-speed control[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 59-68.

[12] 丁磊,尹善耀,王同晓,等.结合超速备用和模拟惯性的双馈风机频率控制策略[J].电网技术,2015,39(9):2385-2391.

DING Lei, YIN Shanyao, WANG Tongxiao, et al. Integrated frequency control strategy of DFIGs based on virtual inertia and over-speed control[J]. Power System Technology, 2015, 39(9): 2385-2391.

[13] YUAN Xibo, LI Yongdong. Control of variable pitch and variable speed direct-drive wind turbines in weak grid systems with active power balance[J]. IET Renewable Power Generation, 2014, 8(2): 119-131.

[14] 赵晶晶,吕雪,符杨,等.基于双馈感应风力发电机虚拟惯量和桨距角联合控制的风光柴微电网动态频率控制[J].中国电机工程学报,2015,35(15):3815-3822.

ZHAO Jingjing, LÜ Xue, FU Yang, et al. Dynamic frequency control strategy of wind/photovoltaic/diesel microgrid based on DFIG virtual inertia control and pitch angle control[J]. Proceedings of the CSEE, 2015, 35(15): 3815-3822.

[15] CHOI J W, HEO S Y, KIM M K. Hybrid operation strategy of wind energy storage system for power grid frequency regulation[J]. IET Generation， Transmission & Distribution, 2016, 10(3): 736-749.

[16] 丁磊,尹善耀,王同晓,等.考虑惯性调频的双馈风电机组主动转速保护控制策略[J].电力系统自动化,2015,39(24):29-34.DOI:10.7500/AEPS20150529018.

DING Lei, YIN Shanyao, WANG Tongxiao, et al. Active rotor speed protection strategy for DFIG-based wind turbines with inertia control[J]. Automation of Electric Power Systems, 2015, 39(24): 29-34. DOI: 10.7500/AEPS20150529018.

[17] YAO Liangzhong, YANG Bo, CUI Hongfen, et al. Challenges and progresses of energy storage technology and its application in power systems[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(4): 519-528.

[18] ZHANG Feng, XU Zhao, MENG Ke. Optimal sizing of substation-scale energy storage station considering seasonal variations in wind energy[J]. IET Generation Transmission & Distribution, 2016, 10(13): 3241-3250.

[19] MIAO Lu, WEN Jinyu, XIE Hailian, et al. Coordinated control strategy of wind turbine generator and energy storage equipment for frequency support[J]. IEEE Transactions on Industry Applications, 2015, 51(4): 2732-2742.

[20] DIAZ-GONZALEZ F, HAU M, SUMPER A A. Coordinated operation of wind turbines and flywheel storage for primary frequency control support[J]. International Journal of Electrical Power & Energy Systems, 2015， 68: 313-326.

[21] 刘巨,姚伟,文劲宇,等.一种基于储能技术的风电场虚拟惯量补偿策略[J].中国电机工程学报,2015,35(7):1596-1605.

LIU Ju, YAO Wei, WEN Jinyu, et al. A wind farm virtual inertia compensation strategy based on energy storage system[J]. Proceedings of the CSEE, 2015, 35(7): 1596-1605.

[22] LEE J, MULJADI E, SORENSEN P, et al. Releasable kinetic energy-based inertial control of a DFIG wind power plant[J]. IEEE Transactions on Sustainable Energy, 2016, 7(1): 279-288.

[23] 李国勇,杨丽娟.神经·模糊·预测控制及其MATLAB实现[M].3版.北京:电子工业出版社,2013.

[24] WU Ziping, GAO D W, ZHANG Huaguang, et al. Coordinated control strategy of battery energy storage system and PMSG-WTG to enhance system frequency regulation capability[J]. IEEE Transactions on Sustainable Energy, 2017, 8(3): 1330-1343.