含软弱夹层的岩质边坡稳定性分析

2018-04-24曹娜

水利规划与设计 2018年3期

曹娜

(阜新蒙古族自治县凌河保护区管理局，辽宁阜新 123100)

随着水利工程的大量兴建，由于滑坡引起的伤亡人数居高不下，对人民生命财产安全造成严重损失，边坡的失稳破坏问题日益突显[1]。边坡的失稳破坏是一个复杂的地质问题，由岩体的结构类型、地貌、风化以及地震等因素共同作用[2]，尤其是软弱夹层的存在使得岩体内部应力的分布变得更为复杂。因此，对含有软弱夹层的岩质边坡进行稳定评价变得尤为迫切。我国学者对含软弱夹层的岩质边坡稳定分析进行了大量的改进和创新，莫晓华等[3]系统总结了边坡稳定分析的各种方法，在Morgenstern-Price法的基础上提出了对条分法普遍适用的平衡方程式，总结了最危险滑裂面的变化规律。谢红建等[4]将数值分析与极限平衡法相结合，建立了简单土坡稳定系数函数，以武都水库坝基为例进行边坡抗滑稳定性研究，得到了临界滑动面的位置变化规律。欧阳吉等[5]将有限元应力分析与自适应遗传算法相结合，对土坡稳定性进行了大量研究分析，验证了方法的可靠性，精度较高，符合工程实际。

本文以白石水库为例，将刚体极限平衡法和有限元软件ANSYS相结合，对含软弱夹层的岩质边坡抗滑稳定性进行分析，探究倾角和主抗滑面起点位置对边坡稳定性的影响规律，综合考虑计算效率和积分精度，得到边坡临界滑裂面的准确位置及安全系数最小值，为含软弱夹层的岩质边坡的稳定性分析提供理论依据，有着重要的现实意义。

1 工程概况

白石水库以供水、灌溉、防洪为主，兼顾养殖、发电、观光旅游，水库地处锦州、阜新、朝阳三市中心地带。白石水库控制流域面积18350平方公里，总投资22.093亿元，总库容18.21亿m3，为辽河三角洲提供农业灌溉用水2.67亿m3。水库大坝为混凝土重力坝，坝顶长5l3.25m，坝高50.31m，包括电站坝段、取水坝段、溢流坝段以及挡水坝段。边坡范围自电站进水口上游100m至坝前总长约700m，滑坡体为残坡积层，由碎石和粉质粘土组成，含量35%左右，粒径6～16cm，结构松散，下游向上游砂岩所占比例逐渐减少，区内岩层褶皱较弱。工程区地下水主要为第四系松散层孔隙水和基岩裂隙水两种类型，地下水的补给以地表水和大气降雨为主，边坡清坡、竖井及洞室开挖未见地下水出露，地下水活动较弱，以裂隙呈渗滴状流水出现，埋深较大。

2 有限元分析

2.1 边坡模型

模型为含有多条软弱夹层的岩质边坡，坡面水平投影为32m，坡角为43.51°，坡高为28.31m，为了便于分析计算，假定在横截面内边坡发生应变和位移，边坡软弱夹层分为第一滑裂面、第二滑裂面和第三滑裂面，模型范围为坡脚下垂直延伸78m，坡顶水平延伸106m，坡脚水平延伸68m。边坡模型如图1所示，模型参数见表1。

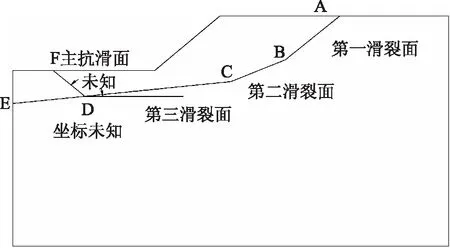
图1 边坡模型

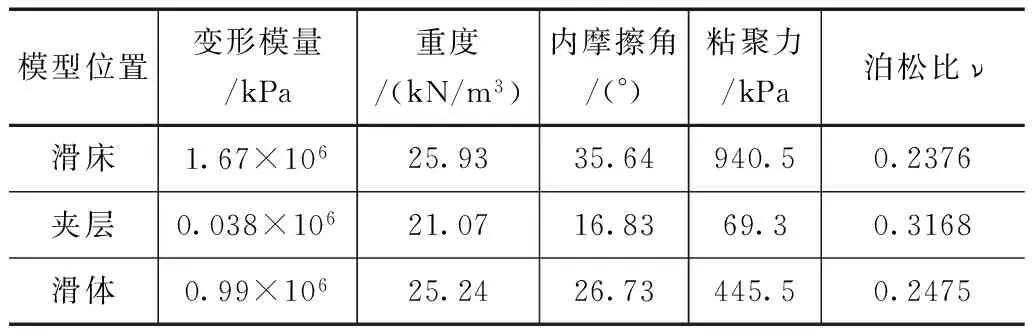
模型位置变形模量/kPa重度/(kN/m3)内摩擦角/(°)粘聚力/kPa泊松比ν滑床1.67×10625.9335.64940.50.2376夹层0.038×10621.0716.8369.30.3168滑体0.99×10625.2426.73445.50.2475

2.2 单元选择

将刚体极限平衡法和有限元软件ANSYS相结合，计算边坡内部应力分布规律，并对应力数据进行处理，得到不同滑裂面上的剪切力，最后实现整体安全系数的计算，并完成主抗滑面的搜索[9]。采用PLANE82单元对岩质边坡进行应变分析，分析精度相对较高，单元具有蠕变、塑性及大应变等特点，每个节点都包含X和Y两个方向的自由度，精度损失较小。边坡弹塑性模拟分析时，将等效摩尔-库伦屈服准则和D-P屈服准则相结合，材料内摩擦角和粘聚力进行转换。

2.3 单元划分及加载求解

为减少计算量并确保计算精度，对边坡模型不同部位进行不同尺寸单元的划分，边坡模型的下部滑床对试验结果影响较小[6- 7]。将软弱夹层及上部滑体部分作为重点研究对象，下部滑床单元边长控制在1m，软弱层单元边长控制在29cm，上部滑体尺寸控制在49cm，边坡模型划分37731个单元、113790个节点。荷载加速度为9.8m/s2，将约束和荷载直接作用在边坡模型上，模型底部施加竖向和水平方向约束，左右边界施加水平方向约束。为了减少计算量同时提高计算精度，选定合理的荷载子步数，选择静态分析类型[8]。模型网格划分如图2所示。

图2 模型网格划分

3 结果分析

3.1 有限元计算结果

采用弹塑性的分析方法，通过有限元软件计算得到边坡水平方向和竖直方向的位移云图，如图3、图4所示。

图3 边坡水平方向的位移云图

图4 边坡竖直方向的位移云图

由边坡位移云图可知，自坡面至坡内深部，竖直方向的位移逐渐增大，软弱夹层的上下两侧，竖直及水平位移均出现不连续现象，当达到一定深度后，位移等值线有变水平的趋势，在第三滑裂面边坡水平方向位移最大为5.132mm，表明软弱夹层对边坡的稳定性的影响占据主导地位。边坡水平方向和竖直方向的应力云图，如图5、图6所示。

图5 边坡水平方向应力云图

图6 边坡竖直方向应力云图

由边坡应力云图可知，在滑裂面附近水平方向应力大小明显不同，坡顶处第一滑裂面的局部区域出现拉应力，坡脚处出现水平方向应力集中现象，在第一条和第二条滑裂面竖直方向应力出现突变。

3.2 滑裂面搜索分析

当边坡失稳时，第三滑裂面与主抗滑面贯通。本文通过第三滑裂面来对主抗滑面的起点位置进行搜索，改变X轴坐标来控制起点的位置变换[10]。起点位置及倾角变化对安全系数的影响较大，因此通过控制单一变量法进行研究，首先固定起点位置，对不同倾角的安全系数规律进行搜索，得到对应的倾角和安全系数；改变起点位置得到最小安全系数的变化规律，进而分析得到安全系数的最小值与主抗滑面的准确位置。不同倾角条件下，起点X坐标对最小安全系数K的影响如图7所示。

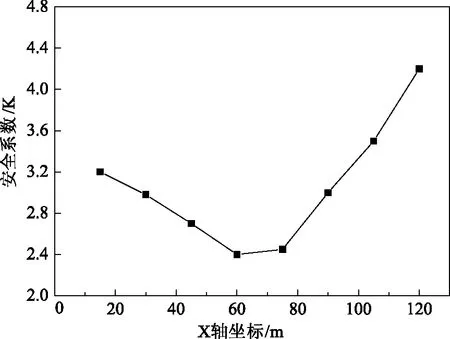
图7 起点X坐标对最小安全系数的影响

由图7可知，随主抗滑面起点位置的变化，最小安全系数呈规律性变化，随着X坐标位置的增大，最小安全系数先减小后增大，并存在最小值，因此能够准确找到主抗滑面位置以及最小安全系数，即主抗滑面的起点位置为(62.3142，71.2063)。为研究倾角对安全系数的影响规律，对不同倾角条件下点(62.3142，71.2063)的安全系数变化规律进行研究，倾角变化对安全系数的影响曲线如图8所示。

图8 倾角变化对安全系数的影响曲线

由图8可知，最小安全系数呈规律性变化，随着倾角的不断增大，安全系数先减小后增大，并存在最小值；当主抗滑面倾角较大时，抗滑面较长，抗滑力增大，不容易滑坡，安全系数较大；当主抗滑面倾角较小时，主抗滑面相对较短，受到的法向

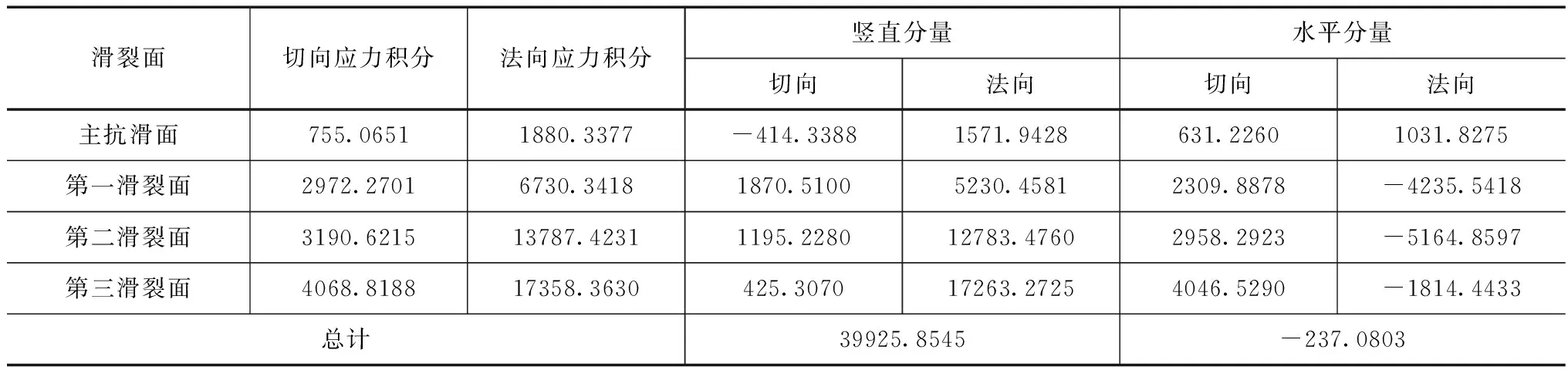
表3 有限元应力积分结果分析(kN)

力较大，抗滑力较大，不容易滑坡，安全系数较大；因此在点(62.3142，71.2063)位置条件下，倾角为155.3125°时安全系数达到最小值K=1.96231。

3.3 应力积分精度分析

为研究网格划分对积分精度的影响，将模型划分为以下五种网格单元，并对不同网格的滑裂面应力积分进行计算，不同网格数量下的应力积分结果，如表2所示。

积分精度通过计算结果与理论值的绝对误差来评定，理论上Y方向的受力为上部滑体的自重，X方向的受力为零。分别将滑裂面上的切向及法向力投影到竖直Y方向及水平X方向，并与理论值作对比。网格数量对积分精度的影响曲线，如图9所示。

图9 网格数量对积分精度的影响曲线

由图9可知，网格划分4222个单元时积分精度为1.5230%，表明有限元应力积分的精度较高，虽然水平方向积分精度和竖向积分精度不同，但是随着网格数量的增加积分精度不断提高。网格数量较少时，Fortran程序及ANSYS软件的运算速度较快，计算效率随着网格数量的增加而不断降低。当网格数量由4222增加到14915时，积分精度增加较快；当网格数量从14915变化到59385时，积分精度增加速度减缓；网格数量超过37731后，积分精度变化曲线基本不变。综合考虑计算效率和积分精度，模型网格划分37731个单元较为合理，竖直方向的积分精度相对较高为0.5301%，水平方向应力积分精度为0.5521%。精度分析过程如表3所示。