大坝下游河道剖面分形与水力因素的关系研究
2018-04-24刘冠霆
刘冠霆,程 炀,张 慧
(扬州市勘测设计研究院有限公司,江苏 扬州 225007)
在河流上修建水利工程,会改变上下游河道的水力特性,对城市防洪、河道演变、航道通航等产生重要影响,研究水利工程对下游河道水力因素的传播和运动规律,对于保证下游防洪和航运安全具有重要意义。
由于水力影响因素众多,在计算分析过程中,很难将所有因素综合考虑,因此一些学者提出用分形维数来代替这些影响因素,进而研究河道的水流特征。所谓分形维数,简单地讲,就是所有不规则形态的自相似程度。对此,一些学者也逐步开展了分形在区域水文要素中的应用研究,并总结了径流、降水等要素的分形特征,提供了这些因素时空变异特性的定量分析方法。金德生等通过研究发现:河道的纵坡降与分形维数之间呈负相关关系,并提出用分形维数与水力因素的关系来预测河流纵剖面的发育趋势。许光祥等则在河道剖面轮廓的分析中,采用亿元分形差值方法,研究了河道剖面轮廓与水力因素之间的自相似性。
本文在总结前人研究方法的基础上,结合长江某段河道,采用一维、二维计算模型分别对河道的纵横剖面进行了分形维数的分析,并得到了分形维数与水力因素之间的关系,并由此分析确定了河道的通航水力指标。
1 河道概况
计算分析河道属长江上游宜宾至朱沱段,全长200多公里。在宜宾和云南水富县交界地带,修建有向家坝水电站,其为金沙江体积开发的最末一级电站。下游河道两岸多低山丘陵,少高山峡谷,河床较为开阔,雨季河道水流宽度为1000m左右,枯水期河道水流宽度在400m左右。该河段主要分布一些浅滩,其次为险滩,急滩较少。该段河道平均比降为0.027%,枯水期平均流速为1.5~2m/s,个别滩涂的最大流速可达4.2m/s。
2 一维、二维非恒定-分形分析模型
2.1 一维分析模型
水力计算一般包括纵向水流的连续和动量方程、纵横向的水流阻力计算以及上下游边界条件等。一维方程以水位Z和流量Q为计算分析要素,在不考虑河道汇流的情况下,河道的连续水流和动量方程为:
连续方程:
(1)
动量方程:
(2)
式中,B—河面宽度,m;Z—水位,m;Q—河道流量,m3/s;x—河段长度,m;a—动量校正系数;μ—河道的平均流速,m/s;g—重力加速度,kg·m/s2;A—河道断面面积,m2;C—谢才系数;R—水力半径。
根据式(1)、(2)计算结果,统计各分段河流的水力因素和河段长度,将流量和河段长按从小到大的方式排列成数列,按如下公式构造一阶和二阶累计和序列:
{S1i}={N1,N1+N2,N1+N2+N3…}i=1,2,3,…,n
(3)
{S2i}={S11,S11+S12,S11+S22+S33…}i=1,2,3,…,n
(4)
将(3)、(4)式计算得到的(S2i,ri)以及(S2i+1,ri+1)在双对数坐标中进行绘制,其斜率即为分河段的分形维数。同理,对所有的(S2i,ri)进行分析,该数据系列的斜率即为该段河道的整体长度分形维数。
2.2 二维分析模型
以笛卡尔坐标系为计算准则,分别采用非结构化网格和三角形网格建立二维水动力模型和模拟复杂的河道边界。其水流连续和运动方程为:
(5)

(6)

(7)
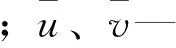
一阶累计数列计算分形维数的方法同(3),即:
{S1i}={N1,N1+N2,N1+N2+N3…}i=1,2,3,…,n
(8)
将得到的数据系列进行线性拟合,其斜率即为计算出河道宽度的分形维数。
3 计算结果分析
3.1 坝下河道纵向剖面的分形维数分析
图1为基于一维分析模型计算得到的该段河道左右岸的整体分维序列情况,从图中可以看到,河道左岸的分维序列与右岸表现得不同,左岸部分分维序列呈先增后减的趋势,部分分维序列又呈递减趋势,右岸的分维序列则是呈逐渐递减的趋势。由于各分维序列点并不呈直线变化,即呈现变维分形情况,这就需要监理变维分形模型对分维序列进行分析,因而采用累计和序列的方式对河道整体长度和分段长度的分形维数进行分析。
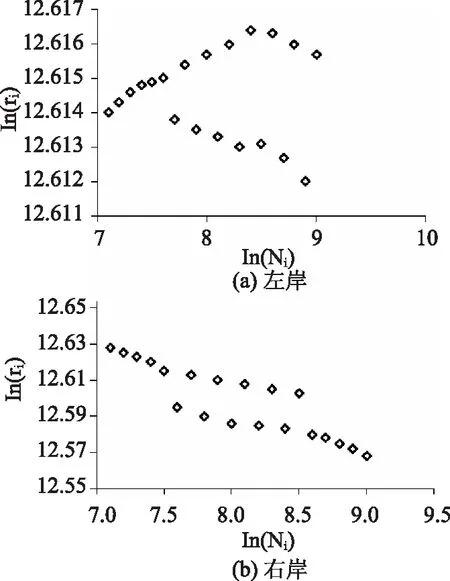
图1 河道整体分维序列
基于累计和序列得到的整体和分段河道的2阶累计和分维序列如图2。从图中可以看到,不管是整体河道长度还是分段河道长度的分维序列,均呈良好的线性关系,表明该段河道纵剖面分形维数呈二阶分维特征。对比左右岸整体长度的分形维数可以知道,左右岸的二阶分形维数相差不大,分别为1.003和1.0021,分段河道宜宾至泸州段的分形维数为1.0269,泸州至朱沱段的分形维数为1.0216,可见,河道的整体分形维数较分段分形维数小。

图2 2阶累计和分维序列
3.2 坝下河道横向断面分形维数分析
基于二维水流计算模型,选取该河段的一个断面(栈桥滩河段断面)进行分析,得到了该河段断面分维序列如图3。图3表明,栈桥滩的断面宽度与河道长度一样,不呈直线关系,仍然为变维分形特征。故也需要对其河道的宽度进行累计序列处理,即用一阶累计和序列。

图3 栈桥滩河段断面分维序列
河道宽度一阶累计和分维序列关系见图4。从图中可以发现,分维序列数据点呈良好的线性关系,分形维数为1.0767,相关系数R大于0.99,表明该滩段的河道宽度呈一阶分维特征。

图4 栈桥滩河段断面一阶累计和序列
3.3 分形维数与水力要素及通航指标关系
图5(a)、(b)分别为分析得到的纵剖面分形维数随流量和横剖面分形维数随水深的变化特征。从图中可以看到随着流量的不断增加,河道的分形维数逐渐降低,这是因为水流量越大,河面淹没的蜿蜒曲折凸出的河岸越多,会使得河道越平缓,越顺直,即河道长度缩短,使得分形维数也就越小。同理,若河道长度越长,分形维数也会越大。河道宽度一定时,横剖面分形维数随着水深的增加而增大,这是因为在相同流量下,河道的宽度取决于河道剖面的形状,水越深河道地形越不规则,即分形维数会越大。

图5 分形维数与水力因素关系
既然河道的纵、横分形维数与流量、水深、流速等水力因素呈一定的相关关系,那么也可基于此基本指标进行航道通航水力指标的判定。将下面四种情况得到的最大流速进行汇总,即为该段河道的最大水流速度:①最小的通航水流量;②上游大坝工程下泄的最大水流量;③该河道的最大比降;④该河道的最小比降。
表1为宜宾-泸州段以及泸州至朱沱段的分形维数与流速的关系。宜宾-泸州段河道的纵剖面分形维数在1.02~1.3之间,河道的比降在0.0257%~0.0263%之间,最大流速不应超过4.12m/s,河道横剖面的分形维数在1.01~1.16之间,此时河道的最大流速不应超过4.18m/s;泸州-朱沱段纵剖面分形维数处于1.035~1.31之间,河道比降处于0.0254%~0.0268%,此时最大流速不超过3.72m/s,横剖面的分形维数处于1.01~1.14之间,最大流速不可超过3.5m/s。因此,综合考虑该段航道的综合情况,认为最大水流速度不应大于3.5m/s。
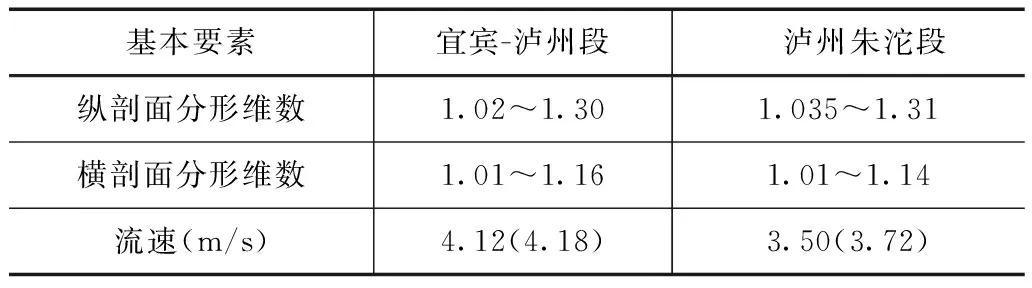
表1 分形维数与该段河道通航水力指标
4 结论
基于一维和二维水力计算模型,对宜宾-朱沱段的纵横剖面分形特征进行了分析探讨,结果表明:纵剖面和横剖面分别符合二阶和一阶分维特性;流量越大,河道越短,纵剖面的分形维数越小,水越深,横剖面的分形维数越越大;该段河道的通航水力指标(最大流速)应为3.5m/s。
[1] 杨文俊, 孙尔雨, 饶冠生, 等. 三峡水利枢纽工程非恒定流通航影响研究Ⅱ: 三峡—葛洲坝两枢纽区间[J]. 水力发电学报, 2006(01): 50- 55.
[2] 曹民雄, 马爱兴, 胡金义, 等. 电站日调节非恒定流对航道整治效果的影响[J]. 水利水运工程学报, 2011(03): 10- 17.
[3] 吴晓黎, 李承军, 张勇传, 等 . 三峡电站调峰流量对航运的影响分析 [J]. 水利水电科技进展, 2003(06): 7- 9.
[4] 董松年. 汉江丹江口水库坝下河床演变及其对航道的影响[J]. 水运工程, 1987(05): 20- 28.
[5] 姜英慧. 基于分形理论的区域水文要素时空变异特征分析研究[J]. 水利规划与设计, 2017(01): 64- 66.
[6] 金德生, 陈浩. 河道纵剖面分形—非线性形态特征[J]. 地理学报, 1997(02): 154- 162.
[7] 许光祥, 钟亮. 河道剖面轮廓的一元分形插值模拟[J]. 人民长江, 2012, 43(03): 20- 23.
