改进粒子群算法的电力系统多 目标无功优化

吴育芝，邹晓松，袁旭峰，熊炜，姚刚

（1. 贵州大学 电气工程学院，贵州 贵阳 550000；2. 贵州电网有限责任公司，贵州 贵阳 550000）

0 引言

无功优化是参考已知的电网参数和负载，通过优化减少有功损耗，电网电压更安全稳定。无功优化控制变量有连续变量、离散变量，约束方程有等式约束和不等式约束。由于无功优化应用问题变量是多维的，传统方法不具备解决能力 。近年来，作为人工智能分支的群体智能引起了许多研究者的关注，应用已成功解决了许多问题。文献[2]列出的智能算法主要包括遗传算法（GE），粒子群优化（PSO），蚁群优化（ACO）等。PSO 算法能够方便解决多维、多目标、离散的最优值，但是易陷入局部最优解[3]。计算潮流是计算无功优化的基础，文献[4]提出了改进的区间潮流算法，对多目标的无功优化求解问题有较好的启示。文献[5]采用免疫算法和免疫克隆算法对电网多目标进行无功优化，并进行对比，计算最优潮流总结出免疫克隆算法有更强的优越性，但还需要考虑实际运用中的问题。文献[6]改进了PSO 算法，其采用加速因子分阶段调整和惯性权重结合（Particle Swarm Optimization with Multi-Strategy Integration，MSI-PSO）求解，得出精度更高。文献[8]进行变量校正的内点法求解最优值，得出能快速收敛。基于改进PSO 的多目标无功优化算法均未能比较好的解决陷入局部最优的问题[9-11]。文献[12]采用改进PSO 算法计算含风电并网的无功优化，采用非线性的惯性权重法改进速度，得出优化效果更佳，但是未考虑收敛因子的。文献[13]采用均衡学习方法优化的智能体算法，对优化思路有意义。本文采用改进PSO 算法，增加惯性权重，改进收敛参数，解决了多目标优化问题。与标准粒子群优化算法相比，它具有平衡局部最优解和全局最优解的能力。

1 多目标无功优化建模

1.1 目标函数

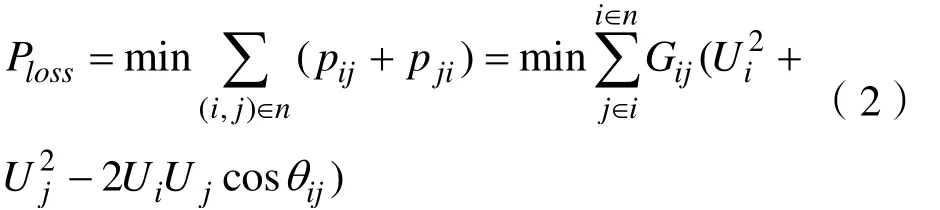
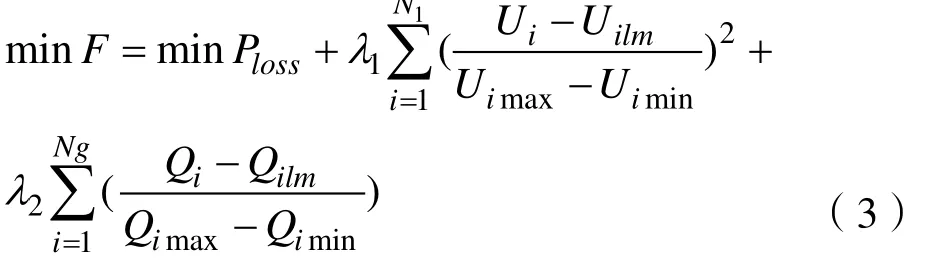
其中 f ( u , x )为无功优化目标函数，g ( u , x ) = 0是一个等式约束， h( u , x ) ≤ 0是一个不等式约束。 在公式中，1λ 、2λ 限制的惩罚参数，ilmU 、ilmQ 是节点i 的电压和无功功率的限制；下标max、min 是上限和下限，ijG 、ijB 、ijθ 分别为线路ij 的的电导和电纳和相角。

1.2 约束变量

等式约束：

在公式中，N 是网格节点的总数；iU 、jU 分别为i、j 各点的电压；GiPLiP 分别为节点i 的发电机的有效输出和有效负载；GiQ 、CiQ 、LiQ 分别为节点i 的节点发电机的无功功率，无功功率补偿容量和无功负载；ijG 、ijB 、ijθ 分别为线路ij 的电导，电纳和相角。

（1）控制变量不等式约束：

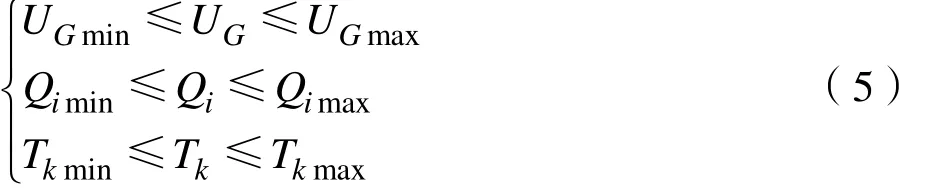
（2）状态变量不等式约束：

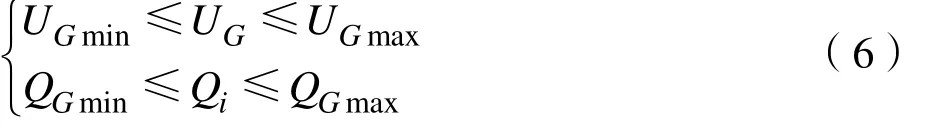
其中， UG、 Qi、 Tk负载变压器的发电机端电压、无功补偿量和有载调压变压器变压器分接头开关。UG、 Qi负荷节点222 电压和发电机无功输出。

2 标准粒子群算法（PSO）

PSO 算法已发展成为一种人工智能算法来解决优化问题。假设一群鸟在一个空间区域随机寻找一块粮食。虽然鸟类一开始并不知道粮食的位置，但它们可以感知粮食与自身之间的距离。在优化问题方面，粮食代表了问题的最佳解决方案，鸟类与粮食的距离代表了功能的适应性。粒子的飞行具有由优化函数确定的适应值，并且每个粒子具有确定其飞行的方向和距离的速度，并且速度的大小通过个体和群体的经验来调整。粒子追踪个别极值，同时追踪全部极值，这样可以更全面地掌握最优解的位置。如下式所示：

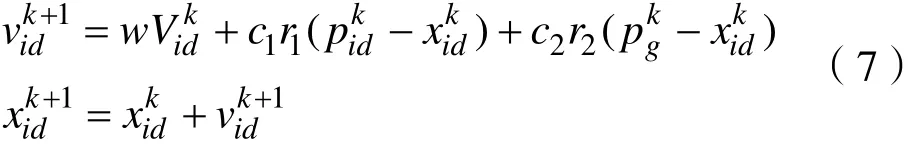
粒子根据公式（7）的速度和位置来更新自己。

3 改进粒子群算法

鉴于PSO 算法容易陷入局部最优，目前改进PSO 有以下几种方法：

3.1 惯性权重线性递减法

引入了惯性权重线性递减法提出的线性递减加权策略。以提高搜索的准确性，如下面的公式（8）所示。

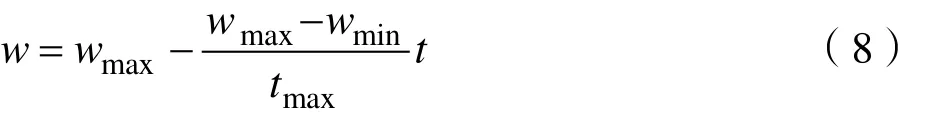
其中 tmax是迭代的最大数量，t 为当前的迭代次数。wmax=0.9， wmin=0.4。

3.2 增加收敛参数

将收敛参数添加到标准粒子群优化算法对于保持多种性的算法是有益的。算法的位置和速度更新公式如下：

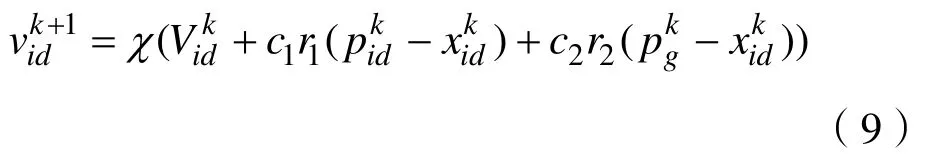
3.3 使用新的位置和速度进化公式

通过粒子的良好体验，尝试在学习过程中离最差位置更远，如下所示：

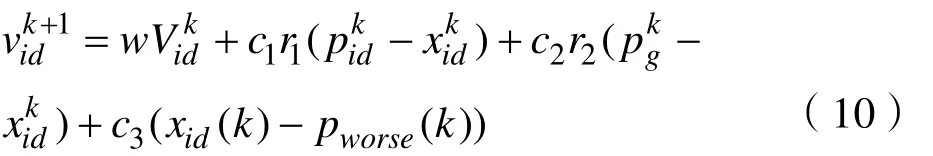
其中， c3加速粒子远离他们所发现的最次位置，pworse( k )是粒子发现的最次位置。

3.4 混合粒子群优化算法

目前有许多的人工智能与基本粒子群优化算法相结合的研究，利用其他算法来弥补粒子群优化算法的不足，提高算法的性能。

3.5 非线性惯性权重线性递减方法和增加的改进收敛参数组合

本文提出采用惯性权重线性递减法和增加改进收敛参数结合的方法改进PSO 算法，具体改进公式如下：

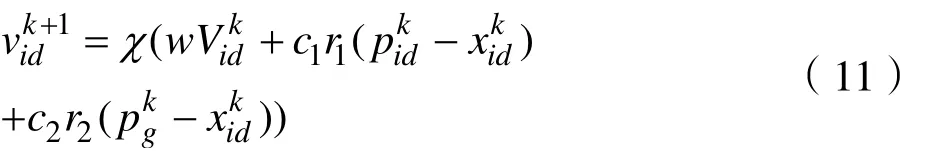
其中，考虑到余弦函数的特性，使在2 的范围内不断放大缩小，期得到最优值。此方法增强了收敛，同时确保搜索精度。算法流程图如下：

图1 改进PSO 无功优化流程图 Fig. 1 Flow chart of reactive power optimization for power system with improved Particle Swarm Optimization

4 算例分析

本文应用MATLAB 语言编写PSO 算法和改进粒子群算法进行无功优化。采用节点IEEE14,潮流计算用Newton-Raphson 法，进行程序编写优化和测试。最后，对优化结果进行比较、分析，如下图2、图3 对比，粒子寻优能力如图4、图5 对比。功率基准值是100MVA，电压幅值为标幺值，实验结果电压偏差稳定在0.85~1.11，对比值如表1 所示，满足电压质量要求。

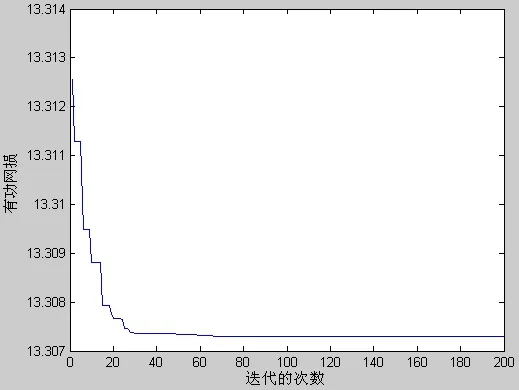
图2 PSO 的无功优化结果图 Fig. 2 The results of reactive power optimization of power system by Particle Swarm Optimization

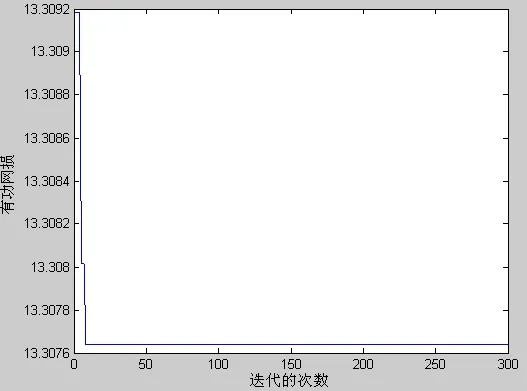
图3 改进PSO 的无功优化结果图 Fig. 3 The results of reactive power optimization for power system with improved Particle Swarm Optimization

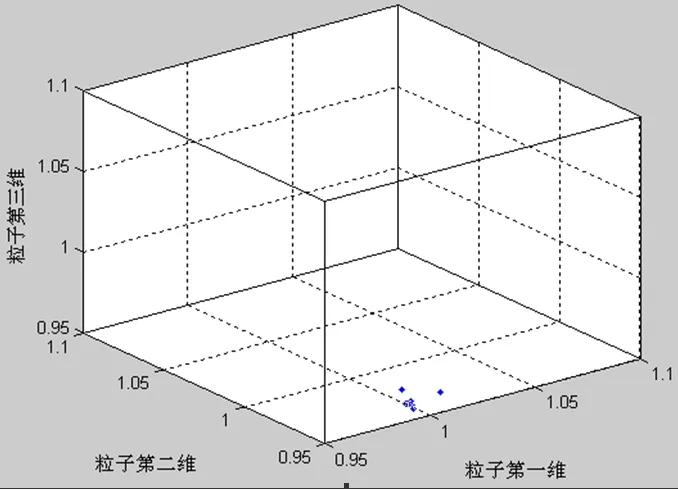
图4 PSO 最终位置 Fig. 4 Final position of particle in Particle Swarm Optimization

图5 改进PSO 最终位置 Fig. 5 Final position of particle in improved Particle Swarm Optimization

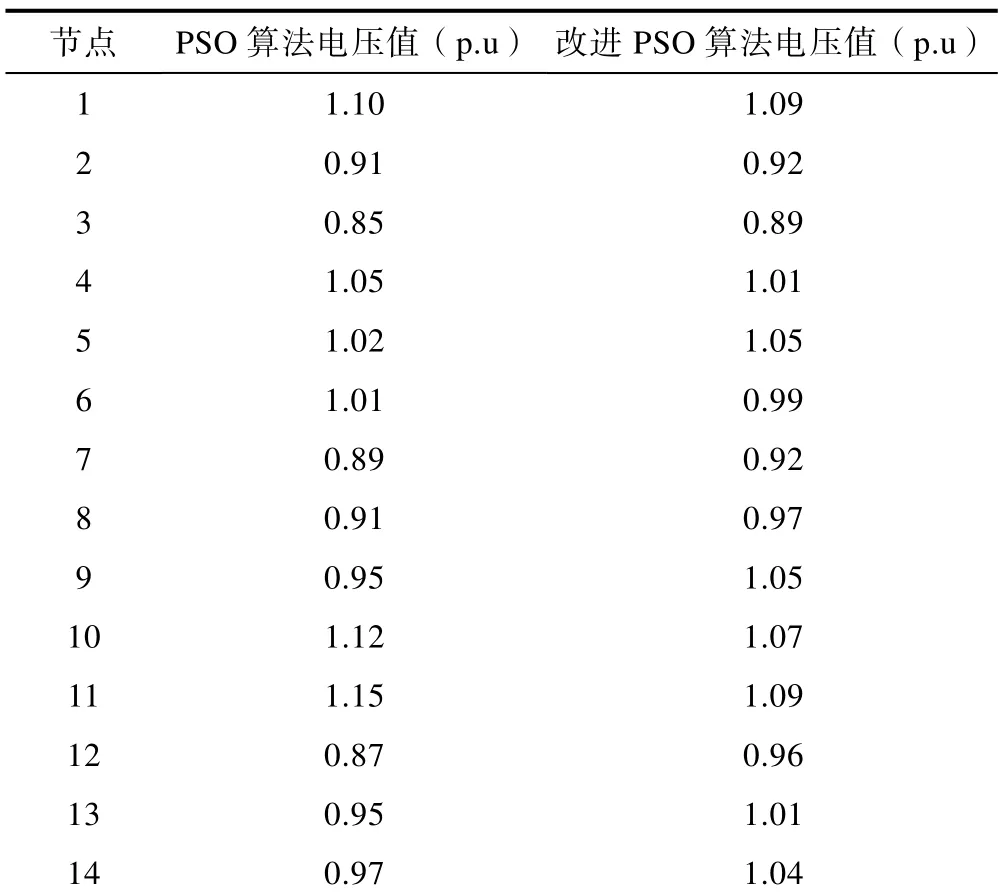
表1 节点电压表 Table 1 Node voltage meter

表2 有功损耗对比 Table 2 Active loss comparison

图2、图3 和表格1、表格2 分析出改进的PSO算法，搜索位置更具有优势，在有功网损降低0.11KW，电压偏差更小，有功损耗值更低，收敛速度更快。

5 结论

从文中可以得出结论：改进粒子群算法无功功率优化结果收敛得更快，收敛值小于未改进之前的收敛值，收敛速度更快。对该例子的分析表明：

（1）利用惯性权重线性回归方法和增加收敛参数来改进粒子群优化算法是有效的，可以使网络有功损耗更小，收敛更快。

（2）有许多方法可以改进多目标无功优化算法，但收敛值区间不是很稳定。本文提出的方法也有所改善，但不可避免地存在这个问题，需要进一步改进，得出更稳定的值。