基于EL 无源控制的VSC-HVDC 的 风电场侧联网建模与仿真
2018-04-24黄世敢
黄世敢
(广东电网惠州供电局,广东 惠州 516003)
0 引言
随着风电技术的快速发展,风电装机容量越来越大,而风电场与负荷中心往往相距甚远,风电场需要通过长距离输电才能并网。对于远距离输电联网,交流输电以及传统直流输电都需要添置无功补偿设备,而VSC-HVDC 技术却可以提供无功支持,所以其更适用风电场联网。所以对于风电场具有远大发展前景的VSC-HVDC 并网方式的研究具有实际意义[1-3]。
1 基于VSC-HVDC 的永磁直驱风电场联网结构

图1 基于VSC-HVDC 的永磁直驱风电场联网结构 Fig. 1 The permanent magnet direct drive wind farm network structure based on VSC-HVDC
基于VSC-HVDC 的风电场联网结构如图1 所 示,其主要由风电场、变压器、换流站,直流输电线路以及电网构成;风电场在论文中采用永磁直驱风电机组构成,而换流站中的变流器采用电压源换流器。
2 VSC-HVDC 换流器的EL 无源控制器设计
欧拉一拉格朗日系统(EL,Euler-Lagrange)是指由欧拉—拉格朗日方程表示的系统。EL 方程的特殊结构能够保证系统耗散性,利用该特性可以简化非线性系统控制器的结构,从而减少大量工作。实际工程中的大部分非线性系统能够用EL 方程表示。系统的无源性结合EL 方程能够设计出无源控制器[4],可以解决实际工程问题。
2.1 风电场侧换流站控制器设计
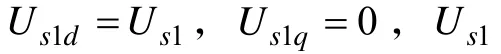

结合VSC 整流器数学模型公式与公式(1),有:
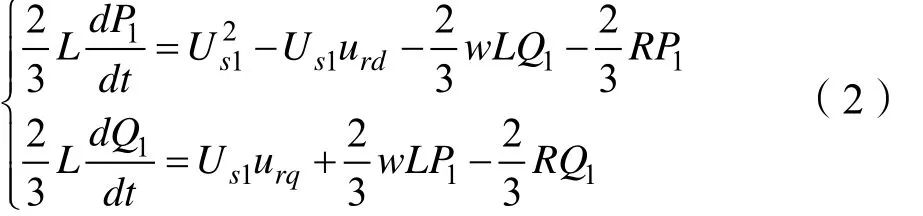

假设式子(3)表示的系统的能量函数用下列式子表示:

将式子(4)进行求导,可得:
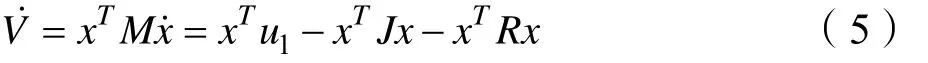
又因为 xTJx= 0,且 xTRx > 0,如此可推导出耗散不等式:

通过系统之无源性判断之法易知,式(3)表示的系统是严格无源系统。
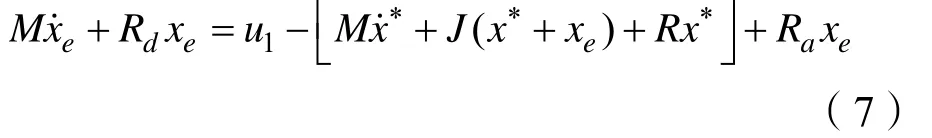
取式子(7)所表示的系统的误差能量函数:

为了使系统的收敛速度加快,增加下式阻尼耗散项:

其中

把式(9)代入式(7),可得:

假设控制率为:
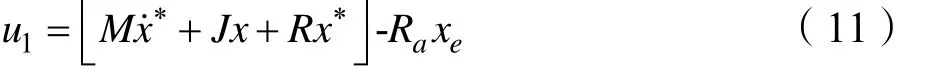
则式(10)转化为:

对式(8)进行求导,可得:
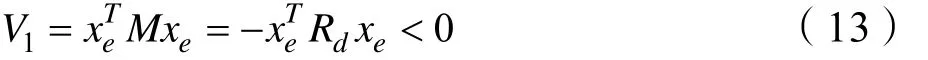
根据李雅普诺夫渐进稳定的定理易知,该系统为渐进稳定性。
由式(11),容易推导出送端站换流器的无源控制律:
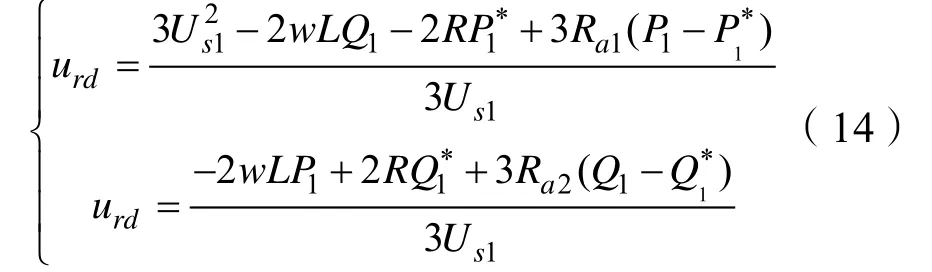
风电场侧换流站控制原理框图见图2。风电场侧换流器需要把风电场侧的全部功率通过 VSC- HVDC 稳定地输送至送端站,且要保证送端站交流侧母线电压稳定,因此风电场换流站选择定有功功率控制与定无功功率控制。
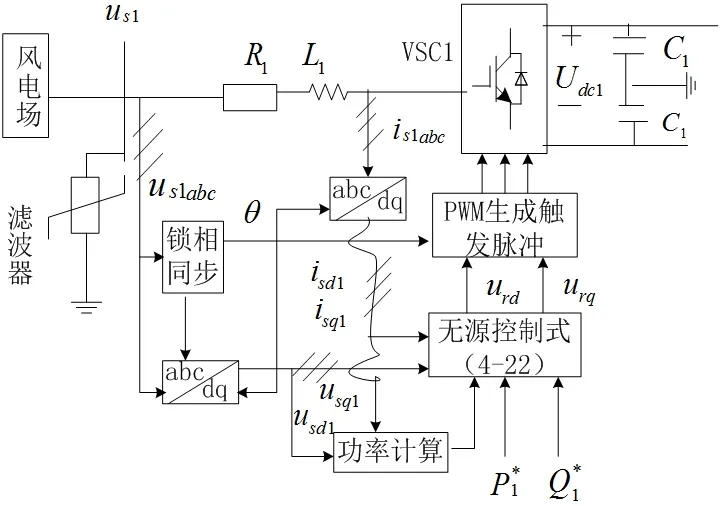
图2 风电场侧换流站控制原理框图 Fig. 2 Wind farm side converter station control principle block diagram
3 仿真分析
在Matlab/Simulink 平台上搭建图1 基于VSC- HVDC 的风电场联网仿真模型,如图3 所示。
风电场侧换流站需要把风电场侧的全部功率通过VSC-HVDC 稳定地输送至送端站,且要保证送端站交流侧母线电压稳定,因此风电场侧换流站采用定有功功率与定无功功率控制。其中风电场的输出功率为风电场侧换流站的有功功率参考值,其数值的大小由风速的大小来决定;而定无功功率控制器参考值为0 pu;
VSC-HVDC 系统额定直流电压100kV,额定有功功率200MW;风电场侧的交流电压分别为25kV;下面分别对系统进行稳态性能仿真分析来验证论文的仿真模型有效性以及控制策略的正确性[5-7]。
3.1 稳态性能仿真分析
以阶跃风作为输入风速,风速在1.5 s 时由12 m/s 阶跃为8 m/s,在2 s 时由8 m/s 阶跃至12 m/s,系统的仿真波形如图4 所示。
从图4(a)可以看出,在1.5s 时,风速减小,风电场侧有功功率随之减小;在2s 时,风速增大,风电场侧有功功率随之增大。表明所设计的无源控制器中的有功功率控制不但都能够可以快速跟踪参考值,而且恢复稳态所需时间短,被控量的稳态控制精度高,验证了论文设计的控制器的有效性。
从图4(b)可以看出,当风电场侧有功功率发生变化时,风电场无功功率上下波动的最大幅度小于0.07 pu,恢复稳定时间小于0.2 s,由此说明风电场侧有功功率与无功功率实现了解耦控制,验证了论文所采用的基于EL 模型VSC-HVDC 非线性解耦控制策略的正确性。
从图5 可知,当风速发生变化时,直流输电线电压的波动最大幅度小于5%,平均波动幅度小于1%,波动时间小于0.25 s,可以近似认为没有发生变化,一直处于稳定状态。由此说明基于 VSC- HVDC 的永磁风电场联网是可行的。

图3 基于VSC-HVDC 的风电场联网仿真模型 Fig. 3 Wind farm network simulation model based on VSC-HVDC
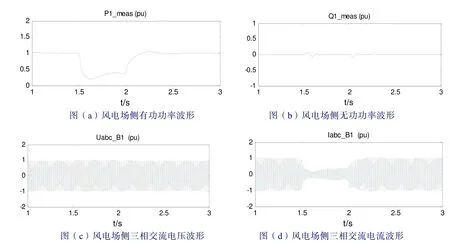
图4 风电场侧仿真波形 Fig. 4 Wind farm side simulation waveform
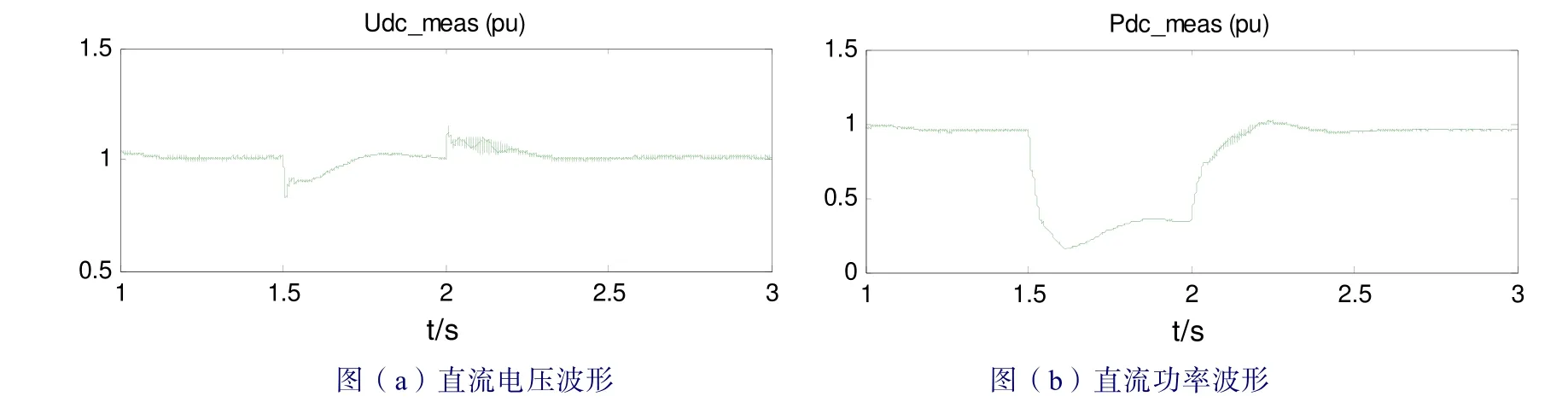
图5 直流侧仿真波形 Fig. 5 Dc side simulation waveform
4 结论
通过改变风速进行稳态性能的测试仿真,说明基于EL 模型无源控制的VSC-HVDC 系统鲁棒性高;验证了论文采取的无源控制策略不但能够简化控制器,不用进行微积分的计算,而且动静态性能好,对VSC-HVDC 系统非线性也有很强的针对性,对于工程应用有较高的实用价值。
