交错有坎台阶式溢洪道消能特性的数值分析

鄢煜川，邓 伟，胡 欣

(1.江西省水利科学研究院，江西 南昌330029；2.江西省水土保持科学研究院，江西 南昌330029)

0 引 言

泄水建筑物作为大坝枢纽重要的组成部分，形式多种多样。台阶式溢洪道作为溢洪道的一种，在近几十年逐渐在水利工程中广泛应用[1]。国外学者如Y.Yasuda[2]、M.Takahashi[3]、H.Chanson[4]、D.Stephenson[5]等研究了台阶式溢洪道的水力特性研究，国内田忠[6]、田嘉宁[7]等人也对台阶式溢洪道进行过水力特性的研究。

上述研究对台阶式溢洪道的单宽流量﹑坡度﹑台阶尺寸等做了大量研究，却较少涉及台阶体型的方面[8]，本文提出了交错有坎式台阶溢洪道，将传统的均匀连续等高台阶式溢洪道称为光滑台阶式溢洪道。在台阶末端交错布置低坎，利用数值模拟技术，对比光滑台阶式溢洪道与不同体型的有坎式溢洪道的消能特性，为同类型工程的改扩建提供一定的思路。

1 模型的建立

1.1 理论模型

标准的k-ε两方程模型具有较高的稳定性与精度，但是不适合旋流等各向异性的流动。Realizablek-ε模型在存在旋转及静止流场中，会产生非物理湍流粘性。RNGk-ε紊流模型主要针对了高雷诺数流动，考虑了紊流的各向异性，是模拟强紊动水流的有效模型[9]。

为了更好的研究交错有坎式台阶溢洪道的水力特性，采用数值计算并对结果进行分析。本次模型采用RNGk-ε湍流模型，方程表达式如下[10]：

(1)标准k-ε两方程模型

(1)

(2)

式中：ρ为流体密度，kg/m3；t为时间，s；xi为座标分量；u为分子粘性系数，σk、σε是湍动能k和湍动能耗散率ε对应的特朗普常数，取1.0和1.3；Gk为平局速度梯度引起的湍动能k的产生项；Gb为浮力影响引起的湍动能k的产生项；Ym为表征可压缩湍流脉动膨胀对总的耗散率影响的参数；C1ε、C2ε、C3ε为经验常数，取默认值1.44、1.92、0.09；Sk、Sε为用户定义的源项；μt为湍流粘性系数；Cμ为经验常数，取0.09。

(2)RNGk-ε模型

(3)

(4)

(3)Realizablek-ε模型

(5)

(6)

(7)

(8)

式中，C1为方程常数，其余符号意义同前。

1.2 物理几何模型

模型的建立在某光滑台阶式溢洪道的基础上，于台阶末端布置3种低坎，分别为有坎、一边有坎、交错有坎。计算模型坝高10.00 m，溢洪道由平顶堰、泄槽段及消力池组成，溢洪道宽5.60 m，一孔，平顶堰长5.00 m，台阶段长20.00 m，底坡为1∶2.00，每级台阶宽2.00 m，高1.00 m，共10级台阶。模型如图1(a～d)所示。堰上水头采用0.50 m、1.50 m、3.50 m三种，各体型工况参数如表1所示。

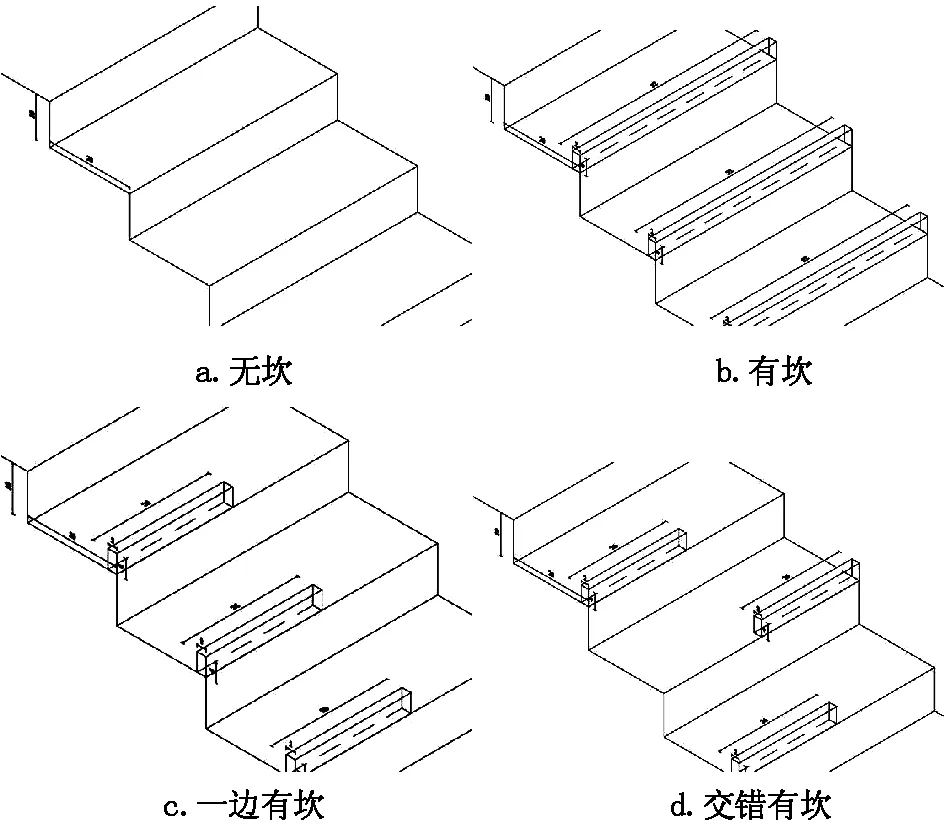
图1 各种台阶式溢洪道

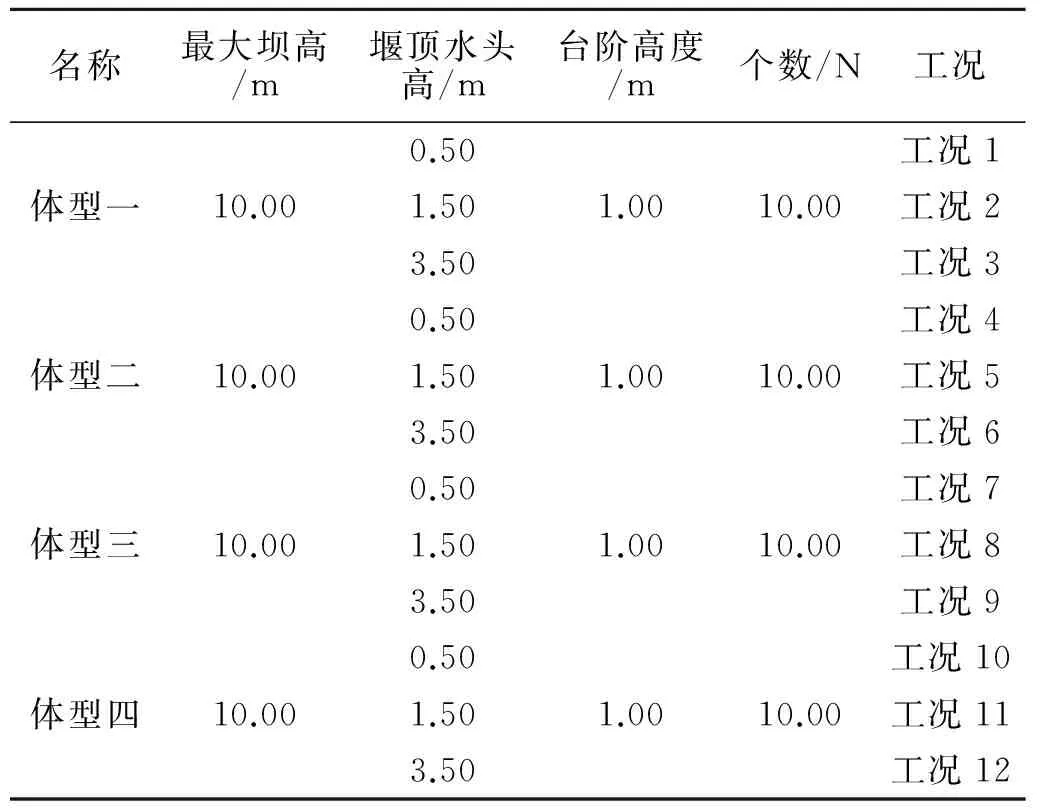
名称最大坝高/m堰顶水头高/m台阶高度/m个数/N工况体型一10.000.501.503.501.0010.00工况1工况2工况3体型二10.000.501.503.501.0010.00工况4工况5工况6体型三10.000.501.503.501.0010.00工况7工况8工况9体型四10.000.501.503.501.0010.00工况10工况11工况12

1.3 网格划分与边界条件设置

(1)计算域。选择堰体上游至下游消力池20.00 m之间的区域进行计算，即图2所示。

(2)网格划分。网格为规则的立方体网格，x、y、z方向长度均为0.20 m，网格总量为60万左右，如图2所示。

(3)边界条件与初始条件。数值计算可将上游面设置为压力进口P并设置相应水位，下游出口采用自由出流O，模型侧壁及底部采用无滑移的固壁边界W，顶部为压力边界P并将压力值设置为0，设置图详见图2。

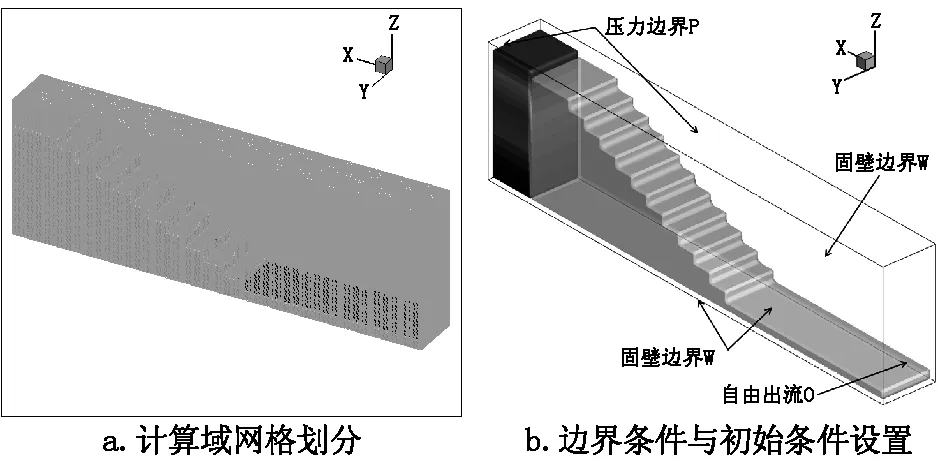
图2 计算域确定

2 数值模拟分析

2.1 流态分析

台阶式溢洪道一般分为3种流态，滑行水流、过渡水流及跌落水流[11]。不同工况流态如图3。

由于种种原因，高职院校的特色资源先天积累不足，后续建设相对滞后，笔者基于高职院校的自身特征，发展方向，人才培养目标，在总结和分析国内高职院校特色资源发展研究成果基础上，提出以下四种协同创新模式，这四种模式并不是独立存在和运行，在实践中完全可以交叉和并行发展。

从图3可以看出，在低水头工况下，4种体型的溢洪道为跌落水流，水流一部分跌落在台阶上形成水跃消能，另一部分留在台阶上形成一定水深。在高水头工况下，4种体型的溢洪道为滑行水流，当水流流过台阶表面时，台阶内被水充满，可以在台阶顶角和主流之间形成旋滚。

图3 流态工况

2.2 消能率

消能率能够直观反映溢洪道的消能效果。计算时可通过能量守恒方程，求得上下游断面的消能效率。消能率η可用下式计算：

(9)

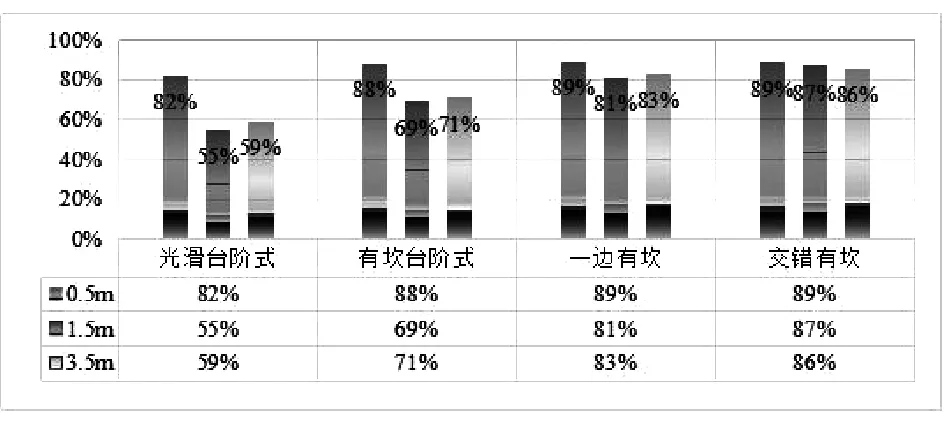
图4 不同工况消能率

从图4可以看出，交错有坎式台阶式溢洪道消能率要大于同水头其他体型的溢洪道，相较于光滑台阶式，在0.50 m水头上消能率提高了7%，在1.50 m水头上消能率提高了36.60%，在3.50 m水头上消能率提高了31.5%。在大流量下，交错有坎台阶式消能率要优于光滑台阶式与其他体型的有坎台阶式溢洪道。

2.3 紊动能与紊动耗散率分布

紊动能与紊动耗散率是反映流体紊动情况的重要参数，可以体现台阶式溢洪道的消能情况。图5为滑行水流工况3、6、9、12下的紊动能及紊动耗散率的分布。

从图5可以看出，同一流量台阶式溢洪道上，紊动能沿程增大后趋于稳定，交错有坎台阶式溢洪道的紊动能较光滑台阶式溢洪道更小，紊动耗散率较大。交错有坎台阶式溢洪道不仅在纵向上形成水深，横向也与上一级台阶下泄的水流进行相互碰撞，进一步加大了消能效果。

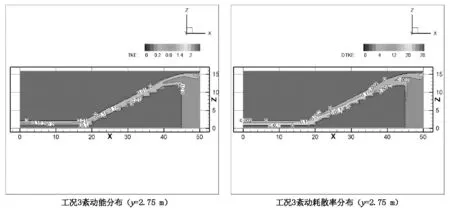
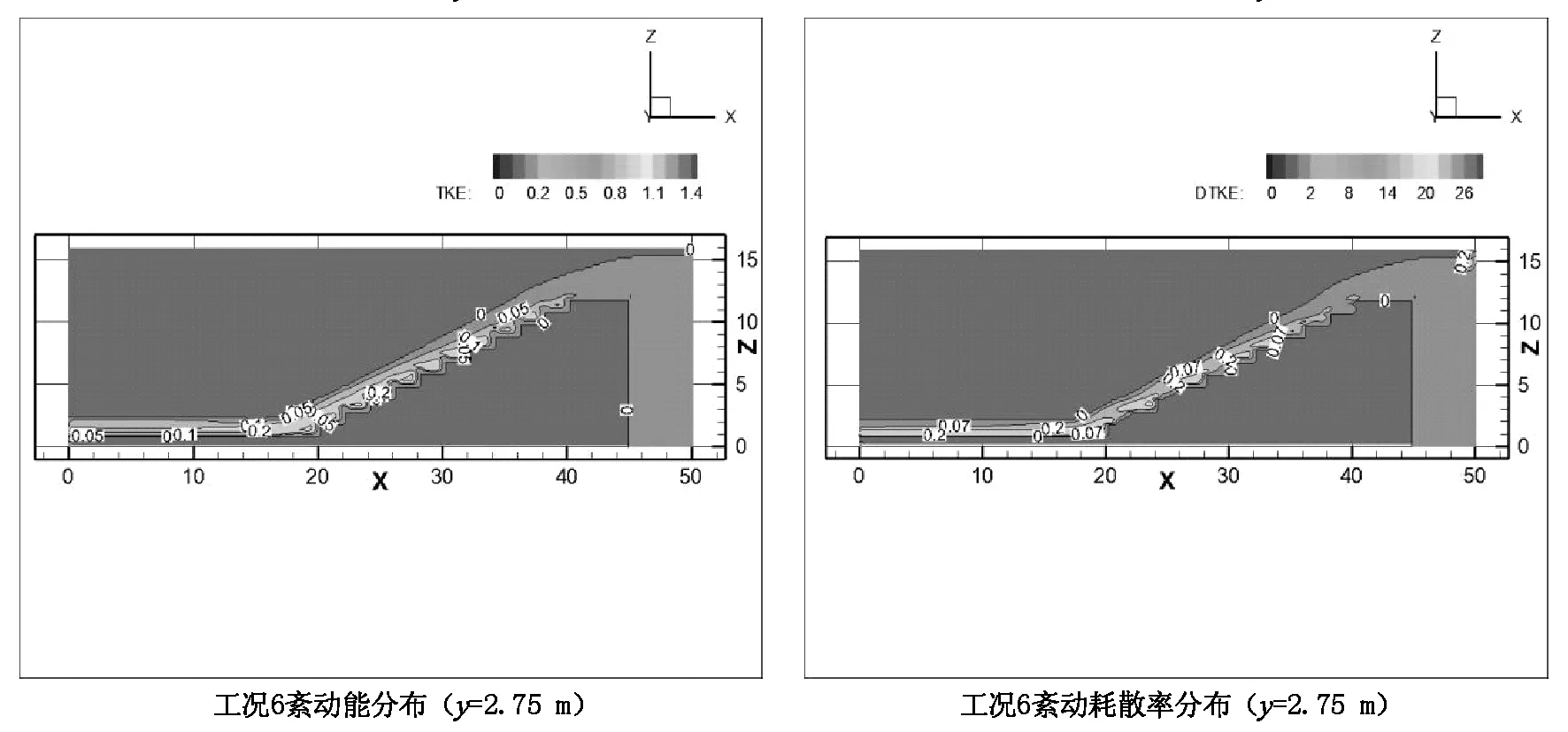
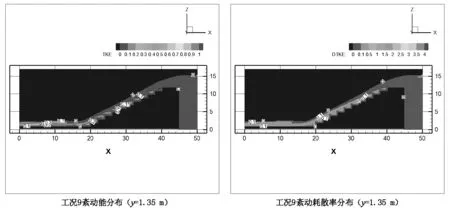
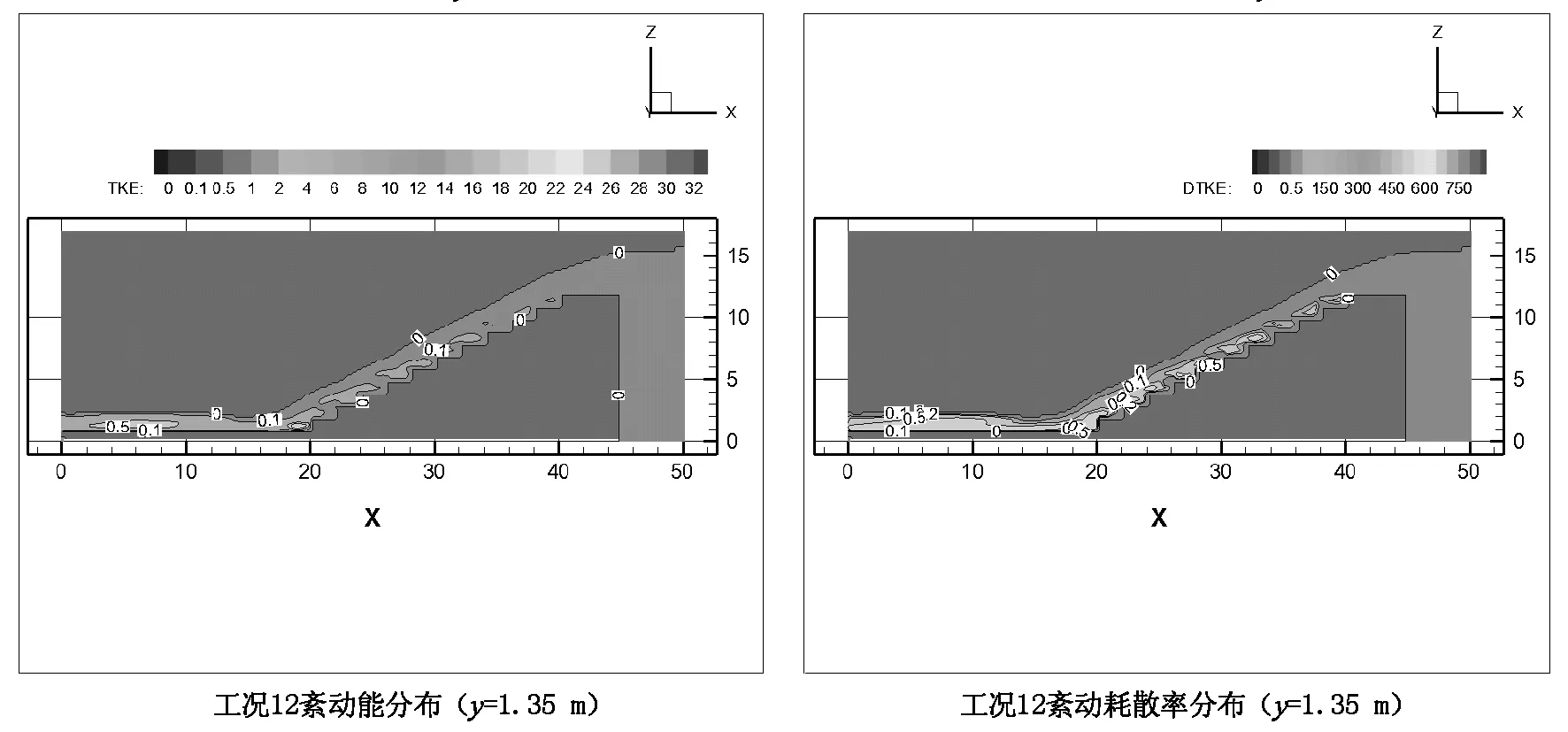
图5 紊动能(左)和紊动耗散率(右)分布

3 结 论

本文通过建立不同体型有坎台阶式溢洪道模型，以光滑台阶式溢洪道做比对，基于数值模拟成果，分析消能率、紊动能与紊动耗散率等参数，反映交错有坎台阶式溢洪道的消能特性。主要结论如下：在大流量下，交错有坎台阶式消能率要大于光滑台阶式；同一流量台阶式溢洪道上，紊动能沿程增大后趋于稳定；交错有坎台阶式溢洪道的紊动能较光滑台阶式溢洪道更小，紊动耗散率较大。基于上面的研究，说明了交错有坎台阶式溢洪道相较于普通光滑台阶式溢洪道有更好的消能效果，可以为今后类似工程的改扩建提供一定的思路。

参考文献：

[1] 王承恩，张建民，李贵吉.阶梯溢洪道的研究现状及展望[J].水利水电科技进展，2008，26(6)：89～93.

[2] Yasuda Y，Takahashi M，Ohtsu I.Enerey dissipation of skimming flow on stepped channel chutes[A].In Proceeding of the 29th IAHR congress，Beijing，2001，9：531～536.

[3] Masayuki Takahashi，Iwao Ohtsu.Nappe flow over horizontal stepped chutes[J].Joural of Hydraulic Research，2011，49(6)：583～590.

[4] H.Chanson，Luck Toombes.Hydraulics of stepped chutes：The transition flow[J].Joural of Hydraulic Research，2011，42(1)：43～54.

[5] Stephenson D.Energy dissipation down stepped spillways[J].Water Power and Dam Construction，1991：27～30.

[6] 田忠，许唯临，余挺，等.“V”形台阶式溢洪道的消能特性[J].四川大学学报(工程科学版)，2010，42(2)：21～25.

[7] 田嘉宁，李建中，大津岩夫，等.几种坡度的台阶式溢洪道消能特性试验研究[J].西北农林科技大学学报(自然科学版)，2004，32(10)：119～122.

[8] 王磊，刁明军，朱润野，等.“M”形台阶溢洪道的消能特性[J].水力发电学报，2015，34(5)：95～102.

[9] 邓伟.块体护底水垫塘水动力特性的数值分析[D].宜昌：三峡大学，2014.

[10] 王福军.计算流体动力学分析-CFD软件原理与应用[M].北京：清华大学出版社，2004.

[11] 田嘉宁，大津岩夫，李建中，等.台阶式溢洪道各流况的消能特性[J].水利学报，2003(4)，35～39.