基于ISVM—逐步回归组合的混凝土坝变形监控模型

王 锋，孙 杨，刘 慧

(江西水利职业学院，江西 南昌 330013)

0 引 言

大坝变形监控模型受多因素的综合影响，其表现为一个复杂的非线性函数关系，对大坝工作性态的模拟和预测，也一直是大坝安全监控研究的重点。目前，常用的安全监控模型有统计模型、确定性模型以及混合模型[1]；研究方法有逐步回归方法[2]和时间序列方法[3]等。近年来，随着一些新型学科的不断发展，神经网络方法[4]、小波分析[5]、支持向量机[6]等方法已应用于混凝土坝的安全监测之中，这些方法为解决大坝工作性态拟合和预报起到了重要作用，但也存在诸多不足。逐步回归方法预报值波动大，部分测值失真可致拟合效果不佳[7]；时间序列方法易受环境量相关性的影响[8]；神经网络方法易陷入局部最优，对初始权值和阈值较敏感[9]；小波分析去噪时易造成大方差，且所得信号可能出现伪吉布斯现象[10]等不足。

针对传统监控模型的不足，依据SVM在处理小样本、高维数、非线性等问题的计算优势，以及其良好的泛化能力[11]，采用改进SVM算法(ISVM)与逐步回归方法结合，有效的弥补了逐步回归方法预报值波动大，部分测值失真可致拟合效果不佳的缺点，利用ISVM算法对影响大坝变形的水压分量进行拟合和预报，并将其预报值与温度分量、时效分量相结合，采用逐步回归方法建立基于ISVM—逐步回归组合方法的大坝变形监控模型，可有效提高模型预报精度。为探究该模型拟合及预测效果，将其结果与逐步回归—逐步回归、ISVM—ISVM及逐步回归—ISVM组合的预报结果进行对比分析。

1 混合预报模型的建立

1.1 大坝位移预报模型中各因子的选取

大坝中任一点的位移δ可表示为水压分量δH、温度分量δT和时效分量δθ三者的叠加，形如[12]：

δ=δH+δT+δθ

(1)

(1)水压分量δH。通常采用逐步回归方法模拟水压分量δH与水位之间的函数关系，其多项式拟合表达式形如：

(2)

式中：ai为回归系数；对于重力坝，常采用三次式，即m1=3；对于拱坝，常采用四次式，即m1=4。

(2)温度分量δT。对于服役时间较长，但大坝工作正常且只有气温观测资料时，坝体内部任一点的温度变化可用周期函数来表示，考虑到位移温度分量与混凝土温度呈线性关系，故选取多周期的谐波作因子：

(3)

式中：i=1时为年周期，i=2时为半年周期，……。n一般取1，2；b1i和b2i为回归系数；t为监测值至始测值累计天数。

(3)时效分量δθ。时效分量综合反映了坝体混凝土及基岩的徐变、塑性变形以及坝体混凝土裂缝导致的不可逆位移和自身体积变形。其一般采用下式表示：

δθ=c1(t-t0)/100+c2ln [(t-t0)/100+1]

(4)

式中：c1和c2为回归系数；t0为基准日期；t为监测日期。

1.2 改进SVM建模原理

改进的SVM模型(ISVM)是在标准SVM模型上进行了改进，通过参数ν实现对经验误差ε的自动计算[13]。设存在一组训练样本集：

T={(xi，yi)|i=1，…，n}，xi∈Rn，yi∈R

(5)

式中：xi为输入数据；yi为目标输出数据。在回归问题中，就是采用一个非线性映射函数φ(x)将样本从原空间映射到高维的特征空间，即从输入空间中Rn到输出空间R上的映射f：Rn→R。设回归函数如下：

f(x)=(ω·φ(x))+b

(6)

式中：ω为全矢量；b为偏置量；x∈Rn；b∈R。

将回归问题视为风险函数最小化问题，回归函数可用风险泛函表示如下：

(7)

其中：

Lε=(yi，f(xi))=max {0，|yi-f(xi)-ε}

(8)

式中：式(7)右侧第一项为规则化项，第二项为经验风险泛化函数；C惩罚参数，通常为常数；Lε(yi，f(xi))为损失函数，常采用不敏感损失函数ε，其取值为估计输出f(xi)与期望输出yi差的绝对值与ε中较大者。

(9)

采用如下约束：

(10)

该二次优化问题的对偶问题如下：

(11)

其约束条件如下：

(12)

求解二次优化问题，得α值及ω的表达式为：

(13)

最终可得回归方程近似解为：

(14)

非线回归问题求解过程中，由于φ(xi)未知，且ω无法显式表达，常采用定义核函数K(xi，xj)[14]来解决非线性映射函数φ(x)具体形式难以确定的问题，核函数形式如下：

K(xi，xj)=(φ(xi)T·φ(xj))

(15)

核函数是通过特征变换的定义使训练样本在特征空间实现某种特征变化。其注重的是变换后的结果，并非变换的具体形式。常用的核函数主要有径向基核函数、多项式核函数及感知器核函数等[11]，不同的核函数对ISVM的影响不大，本文采用较常用的径向基核函数，其具体形式如下：

(16)

式中：σ为核函数参数，其代表方差。

建立ISVM模型的关键对惩罚参数C和核函数参数σ的选取，本文将采用粒子群算法对参数C和σ进行寻优，其中一个粒子即代表一个ISVM模型。

1.3 逐步回归方法

在混凝土坝安全监测中，采用逐步回归分析方法进行大坝变形预测，通过对具有相关关系的荷载集(自变量)及荷载效应(因变量)进行数理统计分析，找出各预报因子对大坝变形的影响，并建立相应的数学表达式，由此推求某一荷载集作用下大坝位移预报值，并与原型观测数据进行比对与残差分析，以此完成大坝的的监测预报。

逐步回归的基本思想是：在建模过程中，将各自变量根据自身对因变量的影响程度大小，以从大到小的顺序依次引入回归方程，为使模型所建立的回归方程具有良好的精度，需随时对回归方程当时所含的全部变量进行显著性检验，若不显著则将其剔除，直到方程中所含的所有自变量对因变量的作用显著时，方可引入新的变量。再在剩下的未选自变量中，选出对因变量影响最大者，检验其是显著性，若显著，则引入方程，否则不引入。直至最后既无显著自变量可以引入，也无不显著自变量需要剔除。

1.4 ISVM—逐步回归组合预报模型的建立

ISVM方法是基于统计学理论的一种新的机器学习算法，该方法可实现由低维空间到高维空间的非线性映射，能较好的解决小样本、非线性、高维数和局部极小值等实际问题，借助ISVM算法可有效解决水压分量拟合过程中的非线性问题[15]。本文采用ISVM算法进行水压分量的拟合和预报，将预报值与温度分量、时效分量进行结合，并采用逐步回归方法建立大坝变形监控模型，基于ISVM—逐步回归组合建立的大坝变形监控模型能够有效的提高模型的预报精度，具体步骤如下：

(1)通过ANSYS软件建立大坝有限元模型，计算各特征水位下大坝某测点的位移值以及各特征水位H对应的H2和H3值；

(2)将各特征水位H值与H2、H3值进行归一化以及降维处理；

(3)利用MATLAB软件，采用粒子群算法对惩罚参数C和核函数参数σ进行参数寻优[16]；

(4)将参数寻优结果结合ISVM算法，建立该大坝测点相应的水压分量预报模型，并对该测点水压分量进行拟合和预报；

(5)将该测点的水压分量预报值与温度分量、时效分量进行结合，采用逐步回归方法建立该测点的大坝位移监控模型；

(6)通过对上个步骤建立的大坝监控模型进行拟合和预报，将预报值与实测值进行对比并展开预报模型预测精度分析。

综上所述，基于ISVM—逐步回归组合方法的大坝变形监控模型的建立流程如图1所示。

2 工程算例

2.1 某混凝土坝有限元模型

某混凝土重力坝坝顶高程179.00 m，最大坝高113.00 m，坝顶总长308.50 m，坝顶宽7.00 m，最大坝底宽84.50 m。水库正常蓄水位173.00 m，调节库容11.22亿m3，校核洪水位177.80 m，相应总库容20.35亿m3。2#坝段有限元模型以六面体八节点单元为主，其中坝体部分共有单元4 463个，节点5 393个；基岩部分共有单元12 440个，节点13 933个，假设有限元模型中弹性模量取24.0 GPa。该大坝共分6个坝段，选取2#典型坝段正垂线测点PL5(179.00 m高程)建立模型，2#坝段有限元模型如图2所示，大坝各特征水位及相应特征水位下的ANSYS计算值如表1所示。

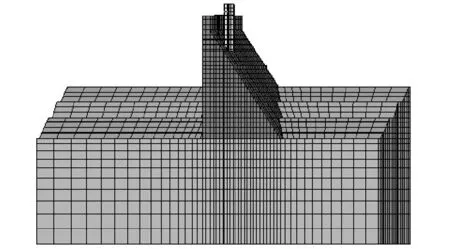
图2 2#坝段有限元模型

2.2 计算结果对比与分析

选取2#典型坝段正垂线测点PL5(179.00 m高程)建立模型，将该测点2006年1月1日～2007年11月1日间的590组监测数据作为训练样本，2007年11月2日～2007年11月11日间的10组监测数据作为测试样本。通过计算得PL5测点在改ISVM—逐步回归组合模型下的拟合和预报结果，并与基于逐步回归—逐步回归、ISVM—ISVM及逐步回归—ISVM组合方法的模型预报结果进行对比分析，结果如图3所示。

由图3可看出，采用4种组合模型的拟合值与实测值的变化趋势相近，表明该4种模型均可用于预报分析，其计算结果存在可比性，模型的精度主要通过预报阶段的预报值体现，为比较4种组合模型的计算精度，将PL5测点在四种组合模型下，于2007年11月2日～2007年11月11日间的10组预报值予以列出，并与实测值进行比对，计算出绝对误差和相对误差，结果见表2。

图3 PL5测点实测值与各组合模型计算值

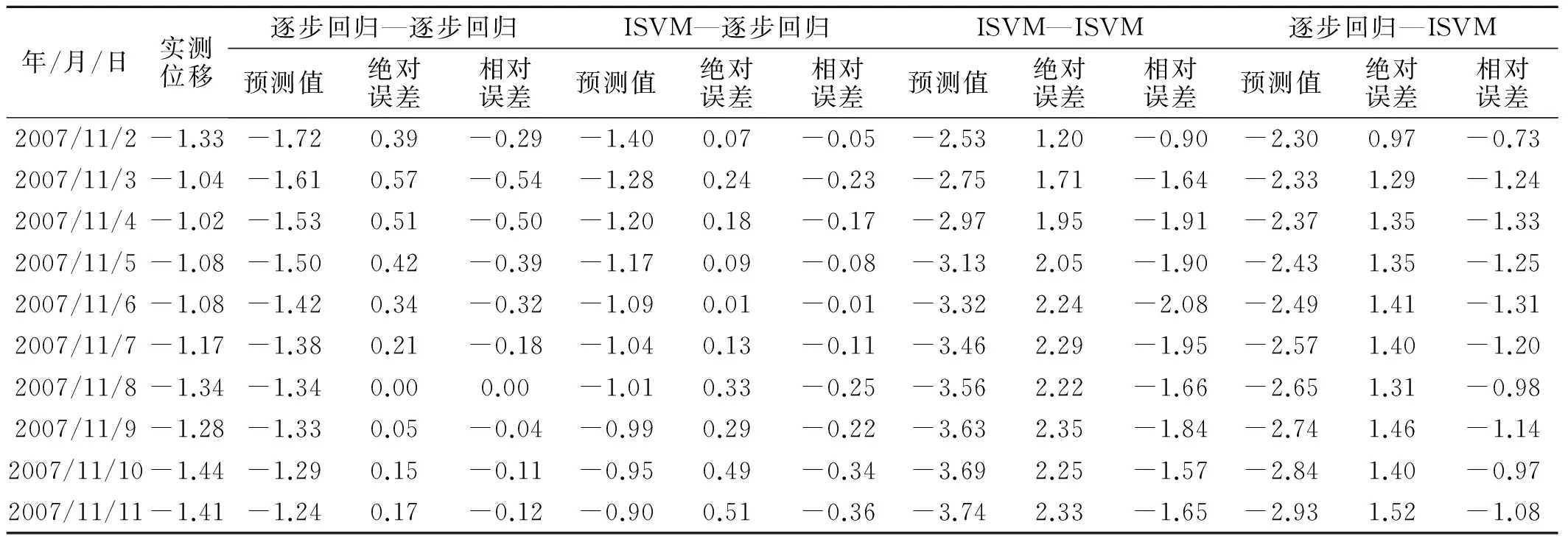
由表2可知，在预报阶段，该测点在逐步回归—逐步回归组合模型和ISVM—逐步回归组合模型下的误差指标总体上要低于ISVM—ISVM组合模型和逐步回归—ISVM组合模型，而ISVM—逐步回归组合模型下的误差指标总体上又要低于逐步回归—逐步回归组合模型，由此可得，此模型预报精度较其他模型有所提高。在采用粒子群算法进行寻优过程中，各参数分别为c1=1.5，c2=1.7，进化代数为60，种群规模为30，寻优速度为3，惩罚系数C范围为[0.1，400]，核函数参数σ的范围为[0.001，0.1]，最终寻优结果为C=400，σ=0.029 141。

为将各组合模型的预报精度表现更为清楚，对该测点在四种模型下的拟合值及预报值的均方误差(MSE)、平均绝对百分比误差(MAPE)等误差指标进行统计，其中MSE可以反映预测值相对实测值的整体变化程度，MAPE可用于衡量预测值与实测值误差的整体水平，计算公式如下：

(17)

(18)

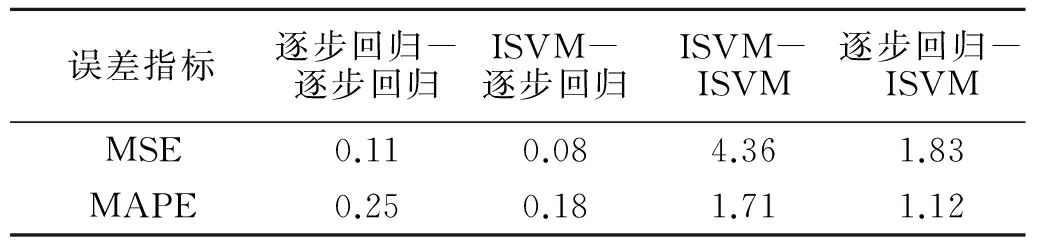
表3 PL5测点各组合模型误差指标对比

由表3可知，在预报阶段，逐步回归—逐步回归模型的精度已经很高，且均高于ISVM—ISVM及逐步回归—ISVM组合建立的模型，而采用ISVM—逐步回归组合建立的模型得到的预报结果可从两项误差指标得以反映，其两项误差指标分别为MSE=0.08，MAPE=0.18，均好于逐步回归—逐步回归模型的两项误差指标MSE=0.11，MAPE=0.25，由此可见，采用ISVM—逐步回归组合可以有效的提高模型预报的精度，这是由于模型中的水压分量是采用ISVM算法进行模拟，该算法是基于结构风险最小原理，能有效的解决小样本、高维数、非线性的问题，能从一定程度上顾及水位与坝体位移间的部分非线性关系，使水压分量的精度得以改善，进而提高监控模型的预报精度，故对于大坝位移监控，采用ISVM—逐步回归方法进行建模将更为合理。

3 结 论

本文通过采用SVM算法对水压分量进行模拟，并结合逐步回归方法建立混凝土坝变形监控模型，有效地将结构计算成果与数据训练方法相结合，体现了大坝在水压力作用下的力学特征，通过采用组合方法构建大坝变形监控模型，可以得出以下结论：

(1)基于ISVM—逐步回归组合建立的的混凝土坝安全监控模型与基于逐步回归方法建立的监控模型相比，拟合精度更高，预测效果更好，将更加适合于大坝监控模型的建立。

(2)在采用ISVM算法进行建模时，研究发现寻优过程中惩罚系数C的范围对模型预报精度的影响较大，其次是核函数参数σ的影响。

(3)在结合水压分量、温度分量及时效分量对大坝建立ISVM模型的过程中，采用粒子群算法对惩罚系数和核函数参数进行寻优时，受高维数的影响，寻优过程较为缓慢，如何提高寻优效率将是以后研究的方向。

参考文献：

[1] 肖浩波，谷艳昌.混凝土坝安全监控最小二乘支持向量机模型[J].长江科学院院报，2013，30(5)：34～37.

[2] 许昌，岳东杰，董育烦，等.基于主成分和半参数的大坝变形监测回归模型[J].岩土力学，2011，32(12)：3738～3742.

[3] 文富勇.基于混沌时间序列的大坝变形监测自适应预测模型[J].水力发电，2013，39(11)：72～76.

[4] 张帆，胡伍生.神经网络融合模型在大坝安全监控中的应用[J].测绘工程，2015，24(1)：53～56.

[5] 刘博智，唐娟.小波分析—回归模型在混凝土坝变形分析中的应用[J].水电能源科学，2012，30(7)：80～82.

[6] 丁世飞，齐丙娟，谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报，2011，40(1)：2～10.

[7] 邱莉婷，沈振中，聂柏松.基于逐步回归分析—马尔可夫链模型的大坝变形预测[J].水电能源科学，2014，32(5)：51～55.

[8] 苏怀智，温志萍，吴中如.基于SVM理论的大坝安全预警模型研究[J].应用基础与工程科学学报，2009，17(1)：40～48.

[9] 王雪红，刘晓青，陶海龙，等.优化BP神经网络的位移预测模型[J].水利水运工程学报，2014，2(2)：38～42.

[10] 袁开明，舒乃秋，孙云莲，等.基于阈值寻优法的小波去噪分析[J].武汉大学学报(工科版)，2015，48(1)：74～80.

[11] SU Huai-zhi，HU Jiang，WU Zhong-ru.A Study of Safery Evaluation and Early-waring Method for Dam Global Behavior[J].Structural Health Monitoring，2012，11(3)：269～279.

[12] 顾冲时，汪亚超，彭妍，等.大坝安全监控模型的病态问题及其处理方法[J].中国科学技术，2011，41(12)：1574～1579.

[13] 丛康林，岳建平，李希灿.v-SVR改进的滚动预测模型在大坝沉降监测中的应用[J].大地测量与地球动力学，2014，34(4)：92～95.

[14] 张倩，杨耀权.基于支持向量机核函数的研究[J].电力科学与工程，2010，28(5)：42～45.

[15] 杜传阳，郑东健，张毅，等.基于动态SVM-MC的大坝变形监测模型及应用[J].水电能源科学，2015，33(1)：71～74.

[16] P.J.García Nieto，E.García-Gonzalo，J.R.Alonso Fernández，et al.Hybrid PSO-MARS-based model for forecasting a successful growth cycle of the Spirulina platensis from experimental data in open raceway ponds[J].Ecological Engineering，2015，81(1)：534～542.