基于协整理论的环境温湿度效应下连续梁桥频率修正方法

何浩祥， 张小福， 王小兵

(1. 北京工业大学 工程抗震与结构诊治北京市重点实验室， 北京 100124;2. 首都世界城市顺畅交通北京市协同创新中心， 北京 100124)

近年来，包括基于模态参数和物理参数、基于现代信号分析技术以及基于智能算法和统计模式识别等方法在内的桥梁损伤评估和状态评估技术迅猛发展，但目前的许多方法都存在着各自的局限性。对于经典的结构损伤分析，一般假定质量保持不变而结构的刚度出现下降。由于频率和刚度是直接相关的，而频率的提取和分析相对简单可行，因此基于频率的损伤评估方法被广泛研究[1]。然而，由于桥梁在运营阶段受到交通荷载、环境因素和噪声的综合作用, 加之工程结构的随机性，实测得到的频率往往出现偏差和不确定性[2]。在实际状态下，由外部因素引起的频率偏差通常与由结构累积损伤引起的频率改变在同一量级甚至更大，这掩盖了结构的真实损伤特征和信息，严重降低了基于频率的损伤评估方法的精确性和可信度，阻碍了该方法的应用和发展。因此，如何对影响桥梁频率的外部因素效应进行有效剥离，提取结构真实动力特性和损伤特征具有重要的理论研究和应用价值[3-4]。

在诸多环境因素中，桥梁的频率、振型等动力特性主要受到温度、湿度和阻尼等宏观环境因素影响。一般认为环境温度对桥梁结构实时动力特性的影响最为显著，因而目前的环境因素影响分析主要局限在温度效应方面。许多研究通过实际工程和试验模型的实测数据并结合桥梁结构形式分析温度效应对桥梁内力的影响规律[5-7]。但在实际研究过程中，湿度同样对桥梁的模态参数有较大的影响，部分研究者对此做出相应研究[8-10]。温度的影响机理主要为：① 温度通过引起钢筋和混凝土的弹性模量的变化从而改变结构的振动频率；② 桥梁为高次超静定结构，温度改变也必然会引起结构内力的改变。由应力刚化理论可知，内力改变也会引起刚度的改变，进而引起频率的改变；③ 环境温度差也会导致桥梁几何形状的改变，使基础边界条件和受力状态发生轻微改变。研究表明结构的动力参数受温度的影响很大，一般认为，温度对桥梁频率的影响主要是由于弹性模量的改变而引起的。湿度的影响机理主要是：混凝土是多孔性材料，湿度将直接影响混凝土结构的含水率，对混凝土材料的力学性能产生影响。随着含水率的小幅增长，混凝土基体相的体积模量变化不大, 但孔隙水的存在对孔隙和裂纹的软化起到了一定的缓和作用，引起混凝土的黏性系数变大，导致混凝土的弹性模量略有增大[11]。由于较慢的滴水渗透过程，湿度对桥梁总体质量的影响较小。

在温、湿度对结构动力特性影响方面，许永吉等[12]研究了温度对多跨连续梁桥动力特性的影响进行了深入研究，结果表明：随着温度的升高, 竖向、纵向和横向的各阶频率呈上升趋势，同时也桥梁边界约束条件的不同而有变化。Peeters等[13]对一座混凝土预应力梁桥进行了10个月的监测, 收集了各项环境数据和振动数据。分析结果表明,该桥的前4阶特征频率的波动范围均>14%，当监测分析得到的频率如果超过理论模型的置信区间则可认为产生温度以外的因素如损伤导致特征频率改变。Ni等[14]以香港汀九大桥长期监测数据为基础，提出利用基于支持向量机(Support Vector Machine, SVM)的非线性回归算法建立频率-温度分布模型从而消除温度影响的方法。Xia等对一块两跨钢筋混凝土连续板进行2年以上的监测，发现温度每上升1℃频率下降0.2%,湿度每上升一度则频率下降0.03%。刘纲等利用结构长期监测信号的多尺度特性，提出较为精确分离温度效应的自适应带宽滤波方法。皮少博以杭州湾跨海大桥北航道为研究对象，运用支持向量机建立数据驱动的模型研究分析温度湿度对该桥模态参数的影响，结果表明绝对温度在0 ℃～30 ℃变化时与频率呈负相关线性变化，绝对湿度与频率成正相关的线性关系。

在以上研究过程中，大部分研究者采用回归分析方法建立环境因素和结构频率之间的关系。虽然线性回归模型可以直观表达环境因素与频率之间的线性关系，但由于环境温湿度和频率序列的非平稳性，对非平稳序列进行线性回归分析存在虚假回归，其样本均值和方差不能准确推断随机变量的分布特征，因此，关于温度或湿度和频率线性回归模型的结果可信性较差。当考虑多环境因素对频率的耦合效应建立自回归滑动平均模型 (Auto-Regressive and Moving Average Model, ARMA)、自回归积分滑动平均模型(Auto-Regressive Integreted Moving Average Model, ARIMA)或扩展ARIMA 模型(ARIMAX)时，ARIMAX 模型引入了外部变量，具有连贯性和类推性，较好地表达多元时间序列的变化规律。但是温湿度以及频率的采集并没有周期性，即同一序列前后之间没有连贯性，并且环境因素影响的研究是针对序列之间的纵向关系的观察，因此相关的ARIMAX差分算法以及延迟算子没有明显的物理意义。近年来协整分析方法日益受到关注并在经济分析和工程领域得到广泛应用。协整理论认为：尽管各个非平稳变量具有各自的长期波动规律，每一个序列的矩会随着时间发生变化，但它们的某种线性组合却可能存在稳定的矩，从而表现出这些非平稳变量之间存在着一个长期稳定的关系，即存在所谓的矩协同持续性，此外协整分析还可以准确反映多变量矩协同持续性。

由于实际的桥梁动力性能受到多环境因素的影响，研究成果大多是通过对监测数据分析得到单独环境因素对具体桥梁的影响和量化统计[15-16]，缺乏对多环境因素综合作用的机理分析和精确模型描述。有鉴于此，本文利用协整分析能够量化多个非平稳序列之间长期均衡关系的能力，提出基于协整分析的频率修正方法。通过对北京地区自然环境下三跨混凝土桥梁模型进行了长期监测，获得了不同环境温度和湿度对结构自振频率的影响，进而建立了基于协整理论的“温度—湿度—频率”长期均衡模型和考虑多环境因素影响的桥梁频率修正模型。

1 协整分析的检验方法及流程

1.1 协整理论及其应用

协整理论是由Engle等[17-18]创建的一种计量经济学分析方法，已成为计量经济学中分析处理非平稳时间序列问题的基本方法。协整基本思想是假定变量自身是非平稳时间序列，而其线性组合可能成为平稳序列，这种平稳的线性组合称为协整方程，可解释为变量之间存在着一个长期稳定的比例关系，即存在长期均衡关系。

在对若干非平稳随机过程进行协整分析之前，必须要使用单位根检验法检验非平稳序列的单整阶数。单整阶数的具体定义为[19]：一个具有非确定性分量的时间序列xt，如果在差分d次后，即Δdxt为平稳序列，而在差分d-1次后仍是非平稳的，则称时间序列xt是d阶单整的，称为I(d)序列，记为xt～I(d)。

Δxt=xt-xt-1,Δ2xt=Δ(Δxt),…,Δdxt=

Δd-1(Δxt)

(1)

式中：Δ为差分运算子。因此，平稳序列可表示为I(0)。

在非平稳性序列单位根检验的结果的基础上，根据检验结果选择合适的变量进行协整分析。若2个或多个变量都是单整变量，且其单整阶数相同，则其线性组合是零阶单整序列时，这些变量即是协整的。协整的定义可以表述为：如果序列[X1t,X2t, …,Xkt]都是d阶单整的，存在协整向量α=[α1,α2, …,αk]，使Zt=αXt～I(d-b)，其中b>0，Xt=[X1t,X2t,…,Xkt]T，则认为序列[X1t,X2t,…,Xkt]是(d,b)阶协整的，记为Xt～CI(d-b)。例如，若序列[X1t,X2t, …,Xkt]都是d阶单整并满足协整关系，则

ξ=α1X1t+α2X2t+…+αkXkt

(2)

式中:ξ为I(0)的平稳序列。

协整分析已被初步应用于健康监测和机械故障诊断，并被证明是行之有效的。这些研究主要运用非线性协整分析方法消除数据中的非线性趋势，并利用由非线性协整分析得到的稳定残差判断结构损伤状态[20]。Cross等[21]采用非线性协整的思想研究Z24大桥基准项目。Zolna等[22]利用非线性协整有效地从各种类型的实验数据消除非线性趋势，得到可靠的风力涡轮机的结构损伤检测的数据。在这些研究中，非线性协整分析方法只考虑了单一因素对结构的影响并且没有量化分析，且不能区分和量化多因素的影响。然而，协整分析最突出的优势是具有确定多个变量之间的协整关系的能力。因此本文考虑环境温度和湿度对结构自振频率的影响，力求建立基于协整理论的“温度—湿度—频率”长期均衡模型和桥梁频率修正模型。

1.2 协整分析过程

钢筋混凝土桥梁的各阶频率会受到多个环境因素的影响，主要是受到来自温度和湿度的影响，而这些环境因素变量往往是非平稳的。如果使用传统的多元回归方法建模，即使回归系数有意义，也会产生伪回归问题。由于协整分析能够有效避免伪回归，可以从变量自身平稳性和变量间的协整关系出发筛选变量、构建考虑多环境因素的桥梁频率修正模型，具有牢固的理论基础和优良的统计性质。

本文力求通过引入线性协整分析方法研究多因素对结构的影响，提出一种基于协整理论的桥梁频率识别模型，力求准确而全面地反映桥梁频率与环境温湿度的关系，为桥梁损伤识别和健康监测提供有效的技术支持。协整分析的基本流程是：为避免出现伪回归问题，首先利用(Augmented Dickey-Fuller,ADF)单位根检验法检验频率、环境温度和湿度等变量的平稳性及其单整阶数；其次，若各变量是同阶单整的，则确立特征方程并进行协整检验，从而明确各变量之间的长期稳定的均衡关系，确立多因素之间的数学模型；最后，深入分析检验结果并剖析机理，并得出修正模型。具体流程，如图1所示。

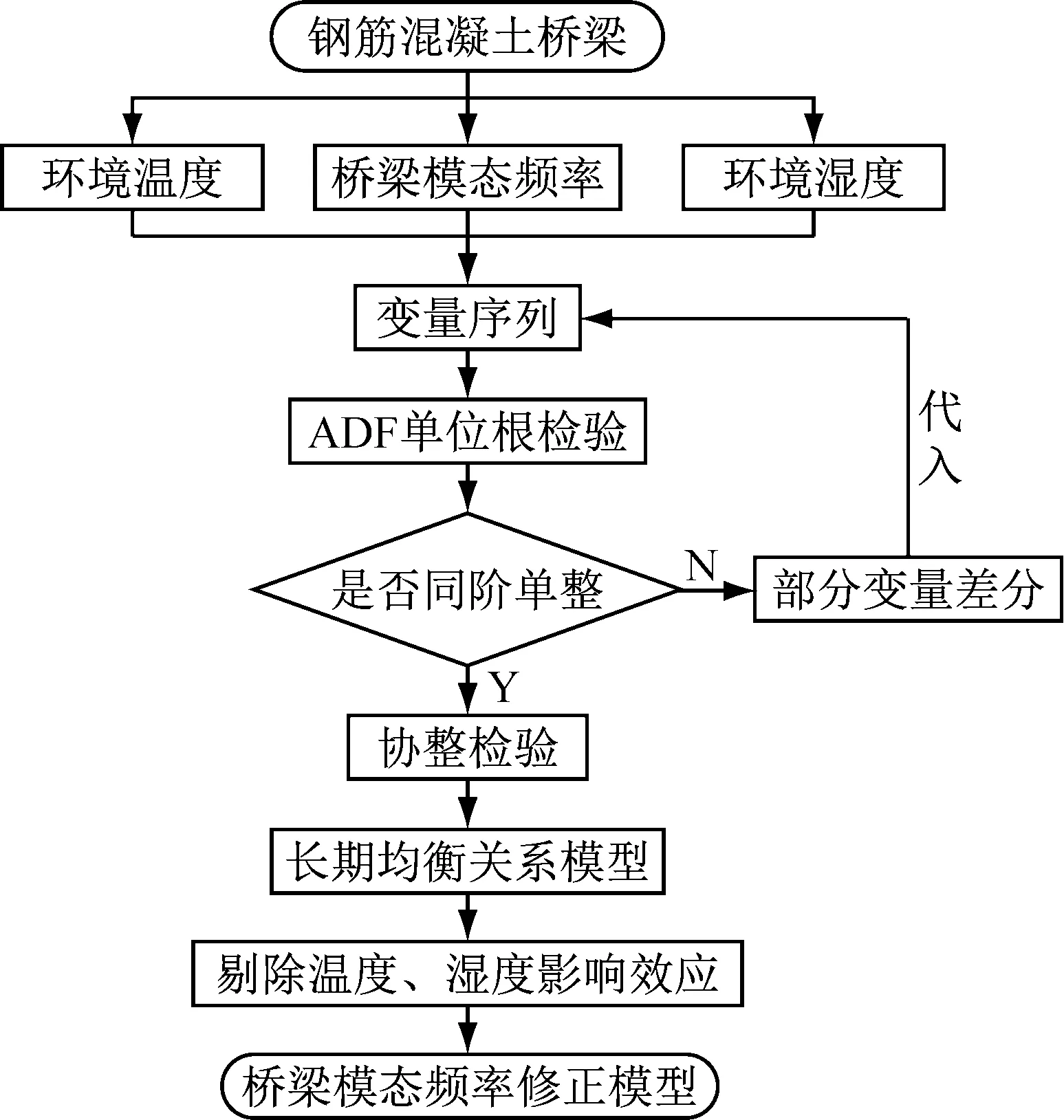
图1 频率修正模型建模步骤

2 混凝土桥梁模型监测数据的采集和处理

2.1 混凝土桥梁模型

环境温度湿度对桥梁频率的影响十分复杂，必须在实测数据分析的基础上建立准确的关系模型，形成有效的环境因素影响的剔除算法，进而在实际工程中应用。为了深入探索预应力混凝土连续梁的桥梁模态参数与环境因素之间的关系，本文以三跨连续梁桥为试验研究对象，根据相似理论的三个相似定理、试验精度要求以及试验条件的可能性，参照实际桥梁建立了缩尺比例为1∶11的桥梁模型，如图2所示。

桥梁模型的跨径组合为3.1 m+3.6 m +3.1 m，截面尺寸及预应力钢筋布置，见图3。通长预应力钢筋采用6Ф5钢丝, 由Фs15.2钢绞线(7根5的钢丝)抽掉中间1根得到,墩顶短束采用3Ф5钢丝, 同样由Фs15.2钢绞线抽出其中4根得到。普通钢筋主要采用Ф6和Ф10的Ⅰ级和Ⅱ级钢筋。混凝土采用C35细石混凝土，其弹性模量为3.15×104N/mm2。该混凝土桥梁模型位于室外，受日光和风雨的直接作用，除自重外，梁上没有任何附加荷载，可以近似地模拟桥梁所处的自然环境。采用无线加速度传感器和无线温湿度传感器进行测试，测点布置，如图4和图5所示。两个测试点分别位于中跨和边跨的跨中。在监测过程中，位于桥梁表面传感器的总质量只有90 g，因此桥梁模型不会因温湿度或试验仪器产生额外的应力，最终得到的模态参数的变化均由自身材料在温湿度变化条件导致力学性能变化而产生的。

图2 钢筋混凝土桥梁模型

2.2 监测数据的采集和处理

为了准确的监测桥梁的模态信息和环境因素变化量，在监测的过程中采用锤击法在桥梁跨中连续施加激励，锤击频率保持恒定，锤击的高度相同，以确保影响效果不变。采用高精度无线加速度传感器采集桥梁竖向振动信息，采用无线温湿度传感器对环境温度湿度进行监测。所有传感器的采样频率均为100 Hz，每个工况采样时间为3 min，并采集相对湿度和摄氏温度作为计算参考量。加速度监测数据采集过程，如图6所示。典型的动力信号和温、湿度监测数据，如图7所示。

(a) 通长预应力筋立面图

(b) 墩顶预应力筋立面图

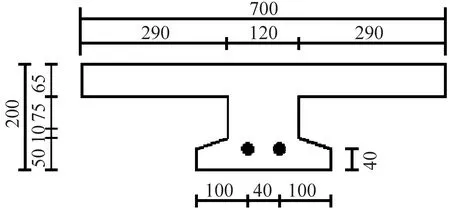
(c) 跨中截面尺寸

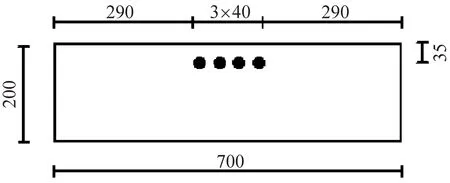
(d) 墩顶截面尺寸

图4 混凝土桥梁模型的测点布置

从2015-09到2016-07期间内，根据温度和湿度的分布，对不同时间段的桥梁的环境信息和模态信息进行采集，得到了大量监测数据。同一环境温度和湿度的影响下，采用多组加速度传感器同时采集，从而保证数据的有效性。在此基础上，对不同环境因素下的数据就进行筛选，删除数据中奇异点，获得有效的监测信息。由于采集过程时间较短，环境温度和湿度变化微弱，因此对采集所得的环境温度和湿度数据求以均值，作为计算环境温度和湿度影响的基本数据。同时对每次采集的桥梁加速度数据进行Fourier变换，得到当时环境下桥梁模型的一阶振动频率。不同环境影响下的频谱分析结果，如图8所示。从图8可知，频率在一定的范围内波动。

(a) 监测数据采集过程

(b) 无线加速度传感器

(c) 无线温湿度传感器

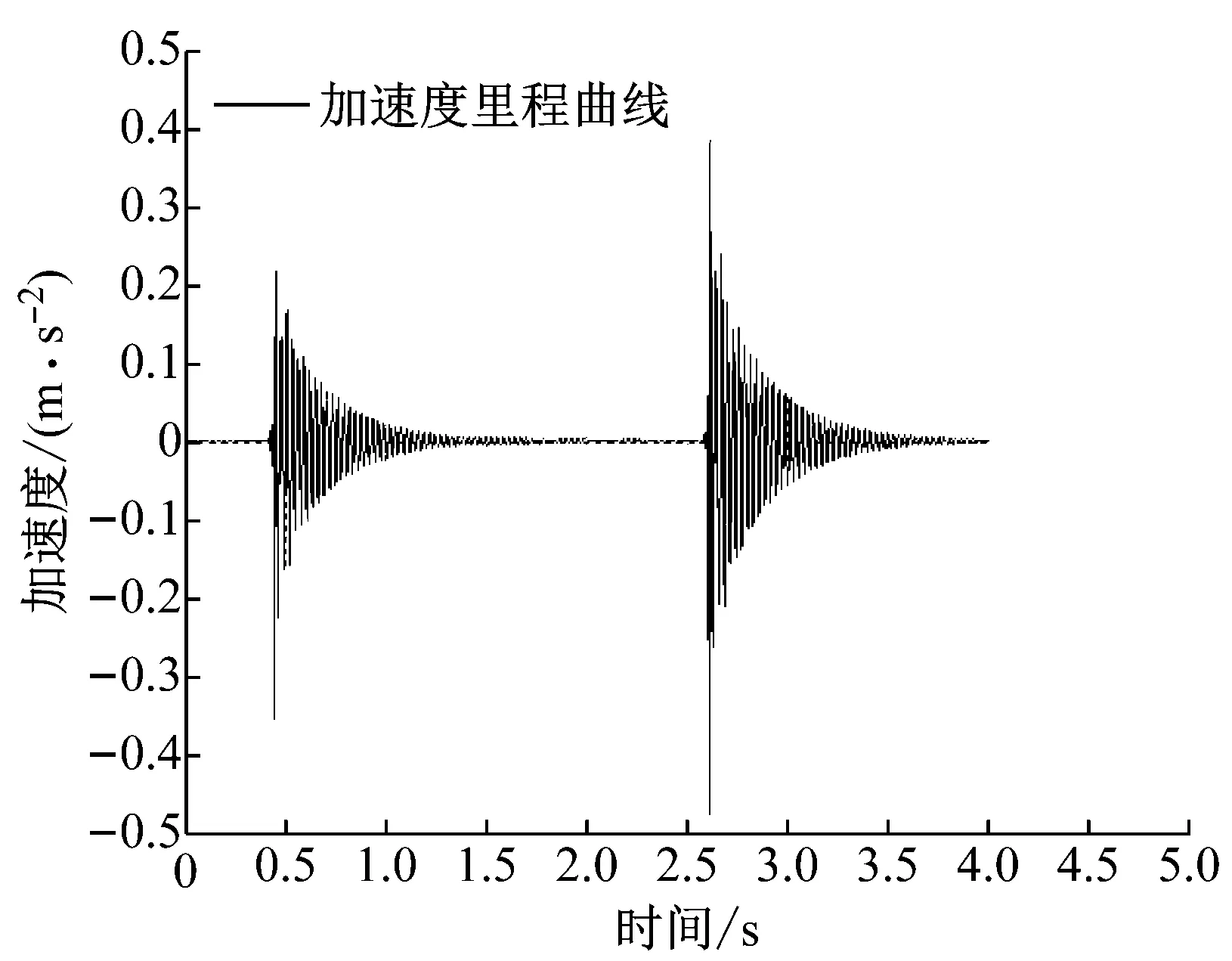
图6 竖向加速度时程曲线

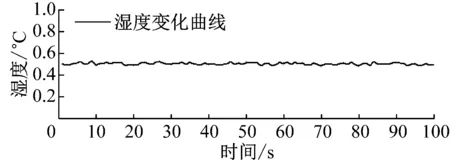
图7 环境温度、湿度时程曲线

3 环境温度和湿度对桥梁频率的影响

3.1 温度或湿度对桥梁频率的单独影响

为了直观地反映模型频率随温度或湿度的变化规律，频率随环境温度的分布，如图9所示，频率随环境湿度的分布，如图10所示。

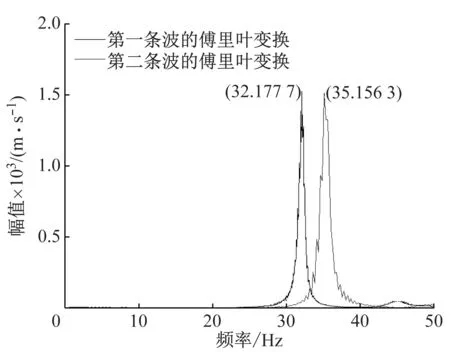
图8 桥梁加速度响应频谱

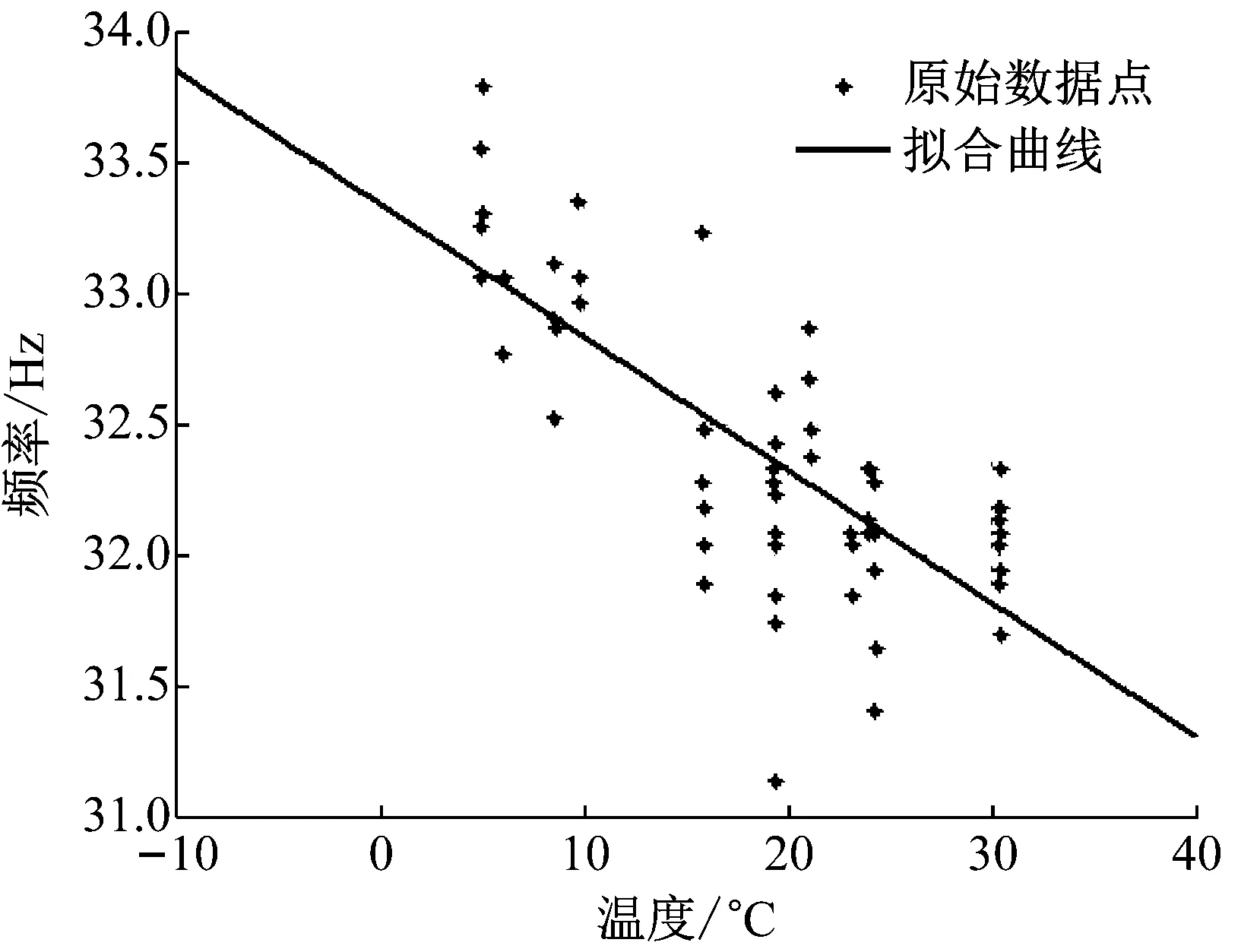
图9 频率与温度散点图

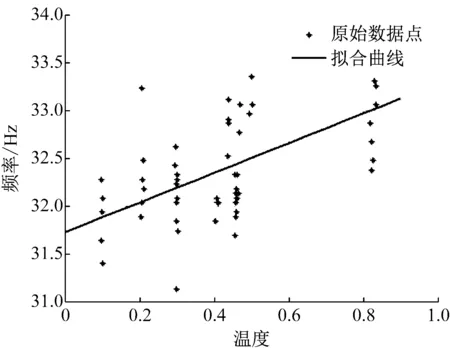
图10 频率与湿度散点图

由以上结果可以看出温度以对频率产生了较大影响，在温度为[-10℃,30℃]区域上进行线性回归时, 虽然部分数据的离散性较大, 但整体相关系数为-0.748，表明温度与频率的变化趋势基本为近似线性。同理，对在湿度为[0,0.9]范围内进行线性回归时，相关系数0.588，表明湿度与频率的变化趋势为近似线性，但线性度相对较低。此外，频率与温度的关系为近似负相关，与湿度的关系为近似正相关。一元线性拟合模型精度偏低，不能充分反映温度或者湿度对频率的影响，更无法表征二者的耦合作用。温度和湿度的变化都会对频率产生显著性的影响，因此当依据实测数据建立环境温湿度与桥梁结构频率的关系时，应当基于协整分析同时考虑温度湿度对桥梁频率的综合影响。

3.2 环境温度和湿度对桥梁频率的综合影响

协整检验的方法有2种：① 1987年Engle和Granger 提出的E-G两步检验法，该方法适用于单方程的协整检验[23]；② 1988 年Johansen以及1990年Juselius提出的Johansen检验方法，其基本思想是基于VAR模型将一个求极大似然函数的问题转化为一个求特征根和对应的特征向量的问题[24]。该方法将协整检验推广到存在多个协整向量的情况。通过Trace统计量不仅能检验出变量之间是否存在协整关系，而且可准确检验出变量间协整关系的个数[25-28]。本文是为了求温度湿度频率三个变量之间的均衡关系，所以采用Johansen检验方法。

由于温度湿度以及频率的采集具有非周期性，需要对其的平稳性进行量化，判断其单整阶数，通过ADF检验来确定。为了对温度湿度以及频率的变化规律有直观的认识并便于选择ADF检验类型，给出各变量的水平项时间序列图和一阶差分项时间序列图，如图11和图12所示。由图中可以发现监测得到的湿度和温度与频率有一定的相关性。

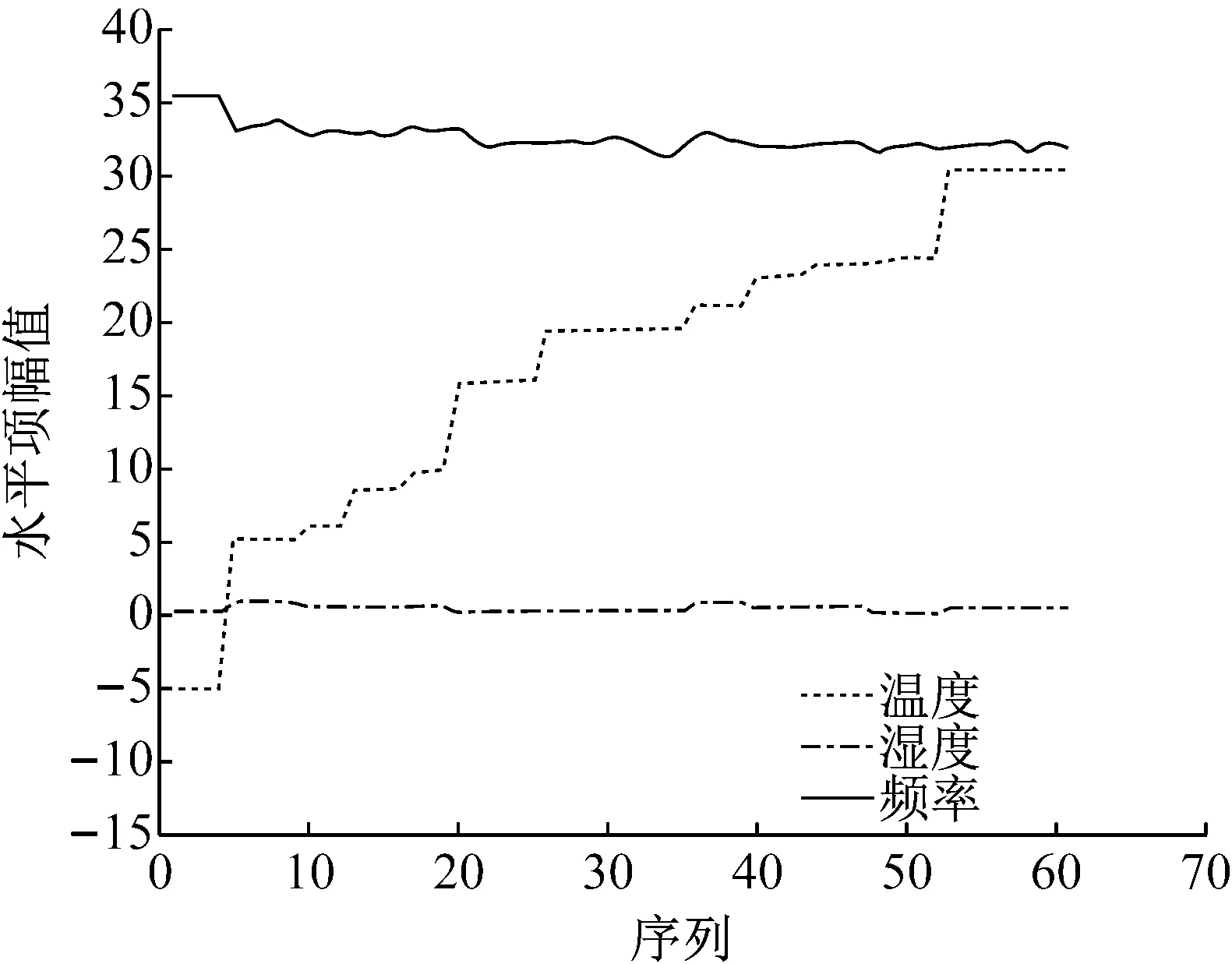
图11 水平项时间序列图

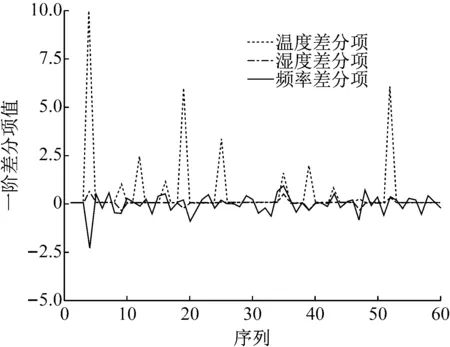
图12 一阶差分项时间序列图

在进行ADF检验时，根据变量以及变量差分项在图11和图12中表现出来的时间趋势选取不同的检验方式，滞后期根据AIC和SC取值最小的原则进行计算。温度湿度和频率的水平项和一阶差分项的ADF检验结果，如表1所示。

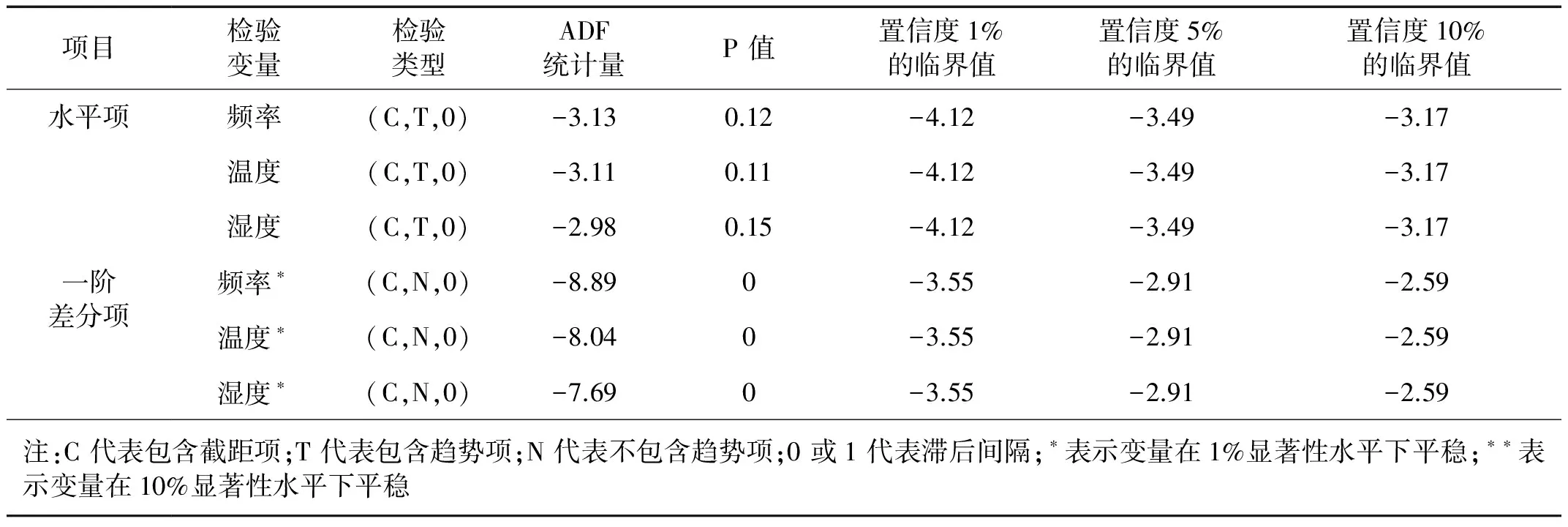
表1 ADF 检验结果

由ADF检验结果可以看出，上述变量温度湿度以及频率均不能拒绝单位根原假设，其一阶差分项均在5%的显著水平下拒绝原假设。即温度、湿度和频率均为非平稳序列而其差分项均为平稳序列，所以原序列式为单整同阶，符合协整检验的前提。由图11可知，温度、湿度、频率序列均有一定的时间趋势，即数据空间中有确定的线性趋势。在确定Johansen 协整检验的方程特征时，协整方程中有截距项，没有趋势项[29-30]。滞后间隔根据AIC(Akaike Information Criterion)值最小准则确定[31]，其检验结果如表2所示。

表2 Johansen 检验结果

注：*表示5%显著水平下拒绝原假设

根据表2的检验结果可知，温度、湿度和频率之间存在唯一的协整关系。通过计算得到标准化的协整向量为[1.000 0.045 -0.907 -32.701]。因此，协整方程可以表示为

fc=0.907H-0.045T+32.701

(3)

式中：fc为桥梁的频率；T与H分别为桥梁环境因素中的温度和湿度。T和H的符号分别为负和正，表示温度与频率负相关，湿度与频率正相关，实际数据和理论分析两者具有较好的一致性。系数值-0.045和0.907分别为频率相对于温度和湿度长期弹性，即温度或者湿度每增长1%，频率增加-0.045%和0.907%。

回代检验和均方误差均可以用于验证方程的拟合效果。将实测的环境温度湿度数据代入“频率—温度—湿度”的长期均衡模型中，得到频率的拟合值，通过对比实测数据和拟合数据验证方程拟合性能，判定拟合方程的准确性。均方误差同样是反应拟合精度的重要参数，定义均方误差σ(x)为误差评判指标

(4)

频率的拟合样本以及实测样本的对比，如图13所示。为了更加客观判定拟合方程的能力，将实测数据和拟合方程表达在三维坐标体系中，其分布，如图14所示。图15为频率的理论模型的拟合残差及其分布。

由图13可知，回代结果表明实测频率都在其拟合频率预测区间范围内，置信度为95%，说明拟合效果较为显著。结合图14可知，随着温度和湿度的变化，基于“频率—温度—湿度”的长期均衡模型得到的频率理论值和实测值是吻合的，两者有较好的一致性，说明了测试数据是客观有效的。从图15可知，残差的概率分布接近于正态分布，即得到的理论模型是无偏估计预测模型，说明理论模型较好的拟合温度和湿度对频率的影响。因此可认为由协整检验得到的“频率—温度—湿度”长期均衡模型有较好的拟合能力，能够准确描述在环境温度和湿度对频率的综合影响。

图13 频率拟合曲线

图14 温度—湿度—频率的三维散点图

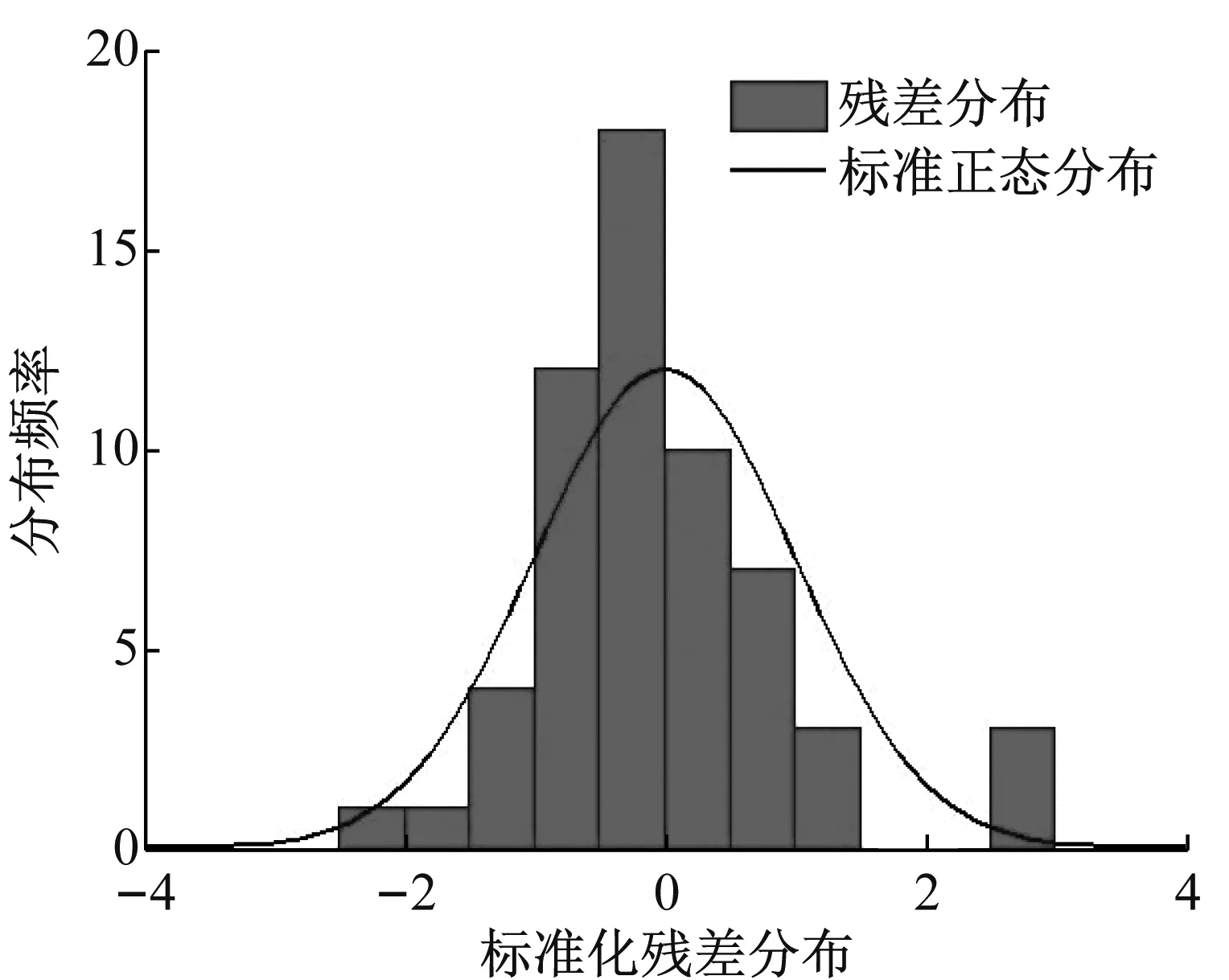
图15 频率拟合残差分布

3.3 频率修正模型的建立及验证

通过协整分析建立了“频率-温度-湿度”的长期均衡模型，量化了温度和湿度的影响，证明了环境温度和湿度的对桥梁频率有显著的影响。在实际桥梁健康监测和损伤诊断中，有必要剔除频率中环境温度和湿度的综合影响，从而实现对桥梁动力特性的精准识别。在此基础上，本文建立考虑环境温湿度的频率修正模型。首先，设定温度和湿度的参考值分别为T0和H0，则实测状态下环境温度和湿度的数值和参考值的关系如下式

(5)

式中:T为测量温度值，ΔT为测量温度与参考温度的差值；H为测量湿度值；ΔH为测量湿度与参考湿度的差值。

由于环境因素的实测值多数情况下不是其参考值，可根据理论模型计算得到温度和湿度单独改变对频率的影响，公式如下

(6)

式中:fc为由长期均衡模型所得的频率，即理论频率。当湿度为定值时，温度的变化对结构频率的影响为fcΔT，同理可得fcΔH。

在实测状态下，要同时考虑温度和湿度对频率的综合影响，由于在长期均衡模型中环境温度和湿度分别对频率的影响是相对独立的，即环境温度和湿度的综合影响为两者单独影响效应之和

(7)

式中:参考环境状态为(T0,H0)，实测环境状态为(T,H)，fcΔT,ΔH为环境温度和湿度对频率的综合影响。

当剔除实测频率中环境温度和湿度的综合影响，修正到统一的参考状态下，该序列才是有效的。修正后的频率可由下式计算

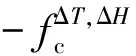
(8)

将式(6)和式(7)代入式(8)，得到桥梁频率修正模型

fm(T0,H0)=fr(T,H)-[fc(T,H)-fc(T0,H0)]

(9)

式中:fm(T0,H0)为修正后的频率值;fr(T,H)为频率的实测值。

在监测期间，混凝土桥梁温度和湿度分布范围有较大波动，因此选取概率较高的温度和湿度作为初始温度T0和初始湿度H0，即定义为20℃和40%。基于标准材料的性能，建立了桥梁的有限元模型(见图16)，通过模态分析得到一阶频率为32.71 Hz。将实测数据代入频率修正模型中，得到修正频率的变化规律。本文混凝土桥梁模型在检测期间处于恒定无损状态，可依据修正后频率序列的分布状态来判断修正模型的准确性。

由以上结果可知，修正频率与有限元分析所得理论频率的差值中，最大正值为0.497 Hz，最大负值为-0.750 Hz；而采集频率与理论频率的差值中，最大正值为1.04 Hz，最大负值为-1.62 Hz。并且修正频率不受温度和湿度的影响，只在理论频率上下随机波动，其差值源于不确定性因素以及测量的随机误差。标准化残差分析表明，误差是随机的，符合标准正态分布。因此，频率修正模型具有良好的剔除环境温度和湿度影响的能力，可用于实际桥梁结构的健康监测以及损伤识别。

图16 消除温度、湿度影响后的频率修正模型

在实际桥梁的健康监测过程中，为了获取完好状态下的频率并进行损伤识别，可以在桥梁竣工后或桥梁运营初期对其动力响应和环境因素进行监测，获得大量的无损状态下的数据。通过协整分析建立频率修正模型，对梁的健康状态健康状态进行有效的识别。

4 结 论

开展关于环境因素对桥梁健康监测和损伤诊断的研究，既可以深入了解结构动力特性的变化规律，又可用利用统计模型来判断导致模态参数变化的因素是属于发生损伤还是环境因素的变化，具有重要的理论和工程意义。因此，为了充分利用频率作为损伤特征参数的优势，且有效地去除环境因素的干扰，本文提出基于协整分析的原理构建的环境因素与频率之间的数学模型和桥梁频率修正模型，为研究桥梁动力特性变化规律和损伤识别提供了一定的依据。

试验分析表明基于协整分析原理建立的温度-湿度-频率的长期均衡模型具有良好的拟合效果，准确地反映了环境因素的耦合效应。混凝土桥梁频率的修正模型可以有效的消除环境因素对频率的影响，使得频率数据更为可靠，为桥梁健康监测和安全评估提供了精准的信息。

[1] MI F, JOHN E T P. The practical limits of damage detection and location using vibration data[C]∥11th VPI & SU symposium on structural dynamics and control. Blacksburg,VA: VPI & SU, 1997: 31-40.

[2] PEETERS B, MAECK J, DEROECK G. Vibration-based damage detection in civil engineering: excitation sources and temperature effects[J]. Smart Materials & Structures, 2001, 10(3):518-527.

[3] ZHANG D, NAGURNEY A. On the stability of projected dynamical systems[J]. Journal of Optimization Theory & Applications, 1995, 85(85):97-124.

[4] NAGURNEY A, ZHANG D. Projected dynamical systems and variational inequalities with applications[M]. Boston, MA: Kluwer Academic Publishers, 1996.

[5] 曾庆响，韩大建，马海涛. 预应力混凝土箱梁桥的温度效应分析[J]. 中南大学学报, 2010, 41(6): 2360-2366.

ZENG Qingxiang, HAN Dajian, MA Haitao, et al. Analysis of temperature effects on prestressed concrete box girder bridges[J]. Zhongnan Daxue Xuebao, 2010, 41(6):2360-2366.

[6] ARIYAWARDENA N, GHALI A, ELBADRY M. Experimental study on thermal cracking in reinforced concrete member[J]. Structural Journal, 1997, 94(4): 432-441.

[7] 张元海, 李乔. 桥梁结构日照温差二次力及温度应力计算方法研究[J]. 中国公路学报, 2004, 11(1): 49-52.

ZHANG Yuanhai, LI Qiao. Study of the method for calculation of the thermal stress and secondary force of bridge structure by solar radiation[J]. China Journal of Highway & Transport, 2004, 17(1):49-52.

[8] XIA Y, HAO H, ZANARDO G, et al. Long term vibration monitoring of an RC slab: Temperature and humidity effect[J]. Engineering Structures, 2006, 28(3):441-452.

[9] 刘纲，邵毅敏，黄宗明. 长期监测中结构温度效应分离的一种新方法[J]. 工程力学,2010, 27(3): 55-61.

LIU Gang, SHAO Yimin, HUANG Zongming. A new method for the separation of structure and temperature effect in long term monitoring[J]. Engineering Mechanics, 2010, 27(3):55-61.

[10] 皮少博. 变环境下的桥梁模态参数分析[D].哈尔滨:哈尔滨工业大学,2015.

[11] 吕文娟. 考虑环境湿度影响的混凝土材料及结构动力性能研究[D]. 北京：北京交通大学, 2015.

[12] 许永吉, 朱三凡, 宗周红. 环境温度对桥梁结构动力特性影响的试验研究[J]. 地震工程与工程振动， 2007, 27(6):119-123.

XU Yongji, ZHU Sanfan, ZONG Zhouhong. Experimental study on effects of environmental temperature on dynamic characteristics of bridge structures[J]. Journal of Earthquake Engineering & Engineering Vibration, 2007, 27(6):119-123.

[13] PEETERS B, ROECK G D. One-year monitoring of the Z24-Bridge: environmental effects versus damage events[J]. Earthquake Engineering & Structural Dynamics, 2001, 30(2):149-171.

[14] NI Y Q, HUA X G, FAN K Q, et al. Correlating modal properties with temperature using long-term monitoring data and support vector machine technique[J]. Engineering Structures, 2005, 27(12):1762-1773.

[15] 杨鸥, 刘洋, 李惠, 等. 时变环境与损伤耦合下桥梁结构频率及阻尼比的统计分析[J]. 计算力学学报, 2010, 27(3):457-462.

YANG Ou, LIU Yang, LI Hui, et al. Cable bridge modal parameter statistical analysis under the time varying environment coupled with damage[J]. Chinese Journal of Computational Mechanics, 2010, 27(3):457-462.

[16] 闵志华, 孙利民, 淡丹辉. 影响斜拉桥模态参数变化的环境因素分析[J].振动与冲击, 2009, 28(10):100-105.

MIN Zhihua, SUN Linmin, DAN Danhui. Effect analysis of environmental factors on structural modal parameters of a cable-stayed bridge[J]. Journal of Vibration & Shock, 2009, 28(10):100-105.

[17] ENGLE R F, GRANGER C W J. Co-integration and error correction: representation, estimation, and testing[J]. Econometrica, 1987, 55(2): 251-276.

[18] BANERJEE A, DOLADO J J, GALBRAITH J W, et al. Co-integration, error correction, and the econometric analysis of non-stationary data[J]. Economic Journal, 1993, 106(439):518-521.

[19] JANACEK G. Time series analysis forecasting and control[M]. Holden-Day: Incorporated, 1990.

[20] CROSS E J, CHEN Q. Cointegration: a novel approach for the removal of environmental trends in structural health monitoring data[J]. Proceedings of the Royal Society A, 2011, 467(2133):2712-2732.

[21] CROSS E J, WORDEN K. Approaches to nonlinear cointegration with a view towards applications in SHM[J]. Journal of Physics: Conference Series, 2011，305(1):012069(1-10).

[22] ZOLNA K, DAN P B, STASZEWSKI W J, et al. Towards homoscedastic nonlinear cointegration for structural health monitoring[J]. Mechanical Systems & Signal Processing, 2016, 75(3):94-108.

[23] ENGLE R F, GRANGER C W J. Co-integration and error correction: representation, estimation, and testing[J]. Econometrica, 1987, 55(2): 251-76.

[24] JOHANSEN S．Statistical analysis of cointegration vectors[J]. Journal of Economic Dynamics and Control, 1988(12): 231-254.

[25] 高铁梅．计量经济分析方法与建模[M]．北京：清华大学出版社，2006.

[26] 钟志威，雷钦礼．Johansen 和Juselius 协整检验应注意的几个问题[J]. 统计与信息论坛, 2008, 23(10): 80-85.

ZHONG Zhiwei，LEI Qinli. Some notes on Johansen and Juselius cointegration test[J]. Statistics & Information Forum, 2008, 23(10): 80-85.

[27] JOHANSEN S，JUSELIUS K M．Likelihood estimation and inferences oncointegration with applications to the demand for money[J]. Oxford Bulletin of Economic and Statistics, 1990(52):169-210.

[28] KITAMURA Y. Likelihood-based inference in cointegrated vector, autoregressive models[J]. Econometric Theory, 1995, 14(4):517-524.

[29] FRANSES P H. How to deal with intercept and trend in practical cointegration analysis?[J]. Applied Economics, 1999, 33(EI 9904-/A): 577-579.

[30] 邓露，张晓峒．ADF 检验中滞后长度的选择：基于ARIMA(0,1,q)过程的模拟证据[J]．数量经济技术经济研究, 2008(9): 126-137.

DENG Lu，ZHANG Xiaotong．The lag length selection in ADF test：simulation evidence from an ARIMA(0,1,q) process[J]. The Journal of Quantitative & Technical Economics, 2008(9): 126-137.

[31] PESARAN M H, SHIN Y, SMITH R J. Structural analysis of vector error correction models with exogenous I (1) variables[J]. Journal of Econometrics, 2000, 97(2):293-343.