融合多绘制算法的复杂场景性能瓶颈分析
2018-04-24李潇瑶
李潇瑶
(四川大学计算机学院,成都 610065)
0 引言
现今,虚拟现实及游戏等领域的热度逐渐高涨,这些领域都将面对来自用户越发严苛的考验,尤其是场景的实时绘制性能及仿真程度。因此,针对这些领域中大规模复杂场景的性能调优和瓶颈检测受到了越来越多的关注。由于这些场景融合了多种不同的绘制算法,因此准确判断出场景性能瓶颈是很困难的。迄今,针对复杂场景绘制性能瓶颈的确定仍大多依据开发者对相关算法的了解及经验人为推定,始终缺乏具体的定量分析。
本文以随机森林算法为基本工具研究基于空间划分的瓶颈分析方法。基于随机森林算法本身的变量重要性(Variable Importance,VI)度量进行特征重要性排序,确定每一子空间内各绘制算法中相关影响因素的重要性,根据二八定律计算子空间内变量重要性比例作为划分空间优劣程度的表达。实验结果表明,本文提出的瓶颈分析方法能够有效划分场景空间,并准确分析得到场景子空间内最重要的性能影响因子。
1 随机森林
随机森林(Random Forest,RF)是 Leo Breiman提出的一种集成机器学习方法,利用多棵决策树对数据进行判别与预测,同时可以评估各个变量的重要性。随机森林主要应用于回归和分类问题,本文主要讨论基于随机森林的回归问题。
1.1 随机森林算法
随机森林由多棵决策树组合而成,每棵决策树之间没有任何关联。随机森林中每一棵决策树都为二叉树,其生长遵循自顶向下的分裂原则。随机森林的构建步骤如下:
(1)使用 Bagging(Bootstrap Aggregating)方法生成训练样本。Bagging方法使用均匀采样,每个样本具有相同的权重。假设原始数据集的样本个数为N,从中有放回地随机选取N个样本作为一个新的训练集,以此构建一棵决策树。通过Bagging方法得到的训练集并不是全部的样本,每次未被抽取的样本组成了袋外数据(Out-Of-Bag,OOB);
(2)随机选取特征(即指瓶颈因素,以下同)对决策树的节点进行分裂。假设共有M个特征,指定一个正整数m< (3)每棵树最大限度地生长,不进行剪枝。 随机生成训练样本以及随机选取特征进行节点分裂,使得随机森林中的决策树都能够彼此不同,降低了单棵决策树之间的相关性,从而提升系统的多样性以及决策效能;因此,随机森林对于噪声数据和存在缺失值的数据具有很好的鲁棒性,具备分析复杂相互作用特征的能力。 图1 随机森林原理示意图 变量重要性度量是随机森林算法的一个重要特性。随机森林常规的变量重要性度量是根据袋外数据(OOB)错误率计算得到,特征Xj Xj的得分统计量用表示。 基于袋外数据的变量重要性定义为袋外数据自变量值发生轻微扰动后的预测准确率与扰动前预测准确率的平均减少量。假设有K个Bootstrap样本B1,B2,…,Bi,…,BK(1≤i≤K),特征Xj(1≤j≤M)的变量重要性度量按照如下方法计算: (1)设置i=1,针对训练样本Bi构造决策树Ti,并将袋外数据标记为 (3)对于特征Xj,对中的特征Xj的值进行扰动,扰动后的数据集记为,使用Ti对数据进行预测,计算扰动后的预测错误率,记为 (4)对于i=1,2,…,K,重复步骤(1)至(3); (5)特征Xj的变量重要性度量通过如下公式进行计算: 由于是通过OOB数据计算的,因此可以看作变量具有的影响能力,没有影响力的变量在数值置换前后的OOB错误率不会发生改变,即数学期望 本文针对融合了多种绘制算法的复杂场景,提出了一种基于空间划分的瓶颈分析方法,利用随机森林的变量重要性度量作为空间划分的主要评判工具,根据二八定律决定空间划分的主要终止条件,通过二叉树的空间划分来建立复杂场景的划分路径,逐次进行迭代,最终得到瓶颈分析模型。 随机森林的变量重要性度量仅仅在全局范围内对影响场景绘制性能的瓶颈因素进行了定量的衡量,但是考虑到绘制算法与场景的空间相关性,可能出现以下几种不同的情况: (1)某一子空间内不涉及任何绘制算法,即该空间内仅仅绘制场景本身; (2)某一子空间内涉及若干绘制算法,即该空间内存在物体及场景部分的交互; (3)某一子空间内涉及所有绘制算法,即该空间内融合了物体及场景所有可能的交互作用,其绘制代价明显高于其他空间。 因此,本文提出了在划分子空间的基础上进一步分析性能瓶颈的思路,并在后续实验部分会展示针对融合了多种绘制算法的复杂场景进行空间划分的实际效果。 对于空间划分的实现,本文约束了特征的空间划分有效性,即只有与空间位置相关的特征允许用于划分空间,反之则视为无效的划分特征。当根据特征Xj(1≤j≤M)用于划分场景空间时,计算当前空间内的变量重要性并按降序排序,根据二八定律统计前20%特征的变量重要性数值总和占所有特征总和的比例,记为,并以同理计算划分后两个子空间内的变量重要性比例,分别记为和场景空间划分需要满足以下两个划分条件: 左右子空间的变量重要性比例的均值应大于上层空间的变量重要性比例; 即左右子空间中任一变量重要性比例小于上层空间的变量重要性比例时,两者的差值仅允许在一定的阈值范围内。 在瓶颈分析过程中,判断当前场景空间是否达到划分终止条件,如果当前空间不满足终止条件,则继续向下划分,反之,则终止该空间的迭代划分,将其置为叶子节点并分析当前空间的瓶颈因素。划分终止条件的计算公式如下: 其中,M为特征个数,80/20的取值参考于巴莱多定律,即二八定律。二八定律认为在任何特定群体中,重要的因数通常只占少数,而不重要的因数则占多数,因此只要能控制具有重要性的少数因数即能控制全局。本文利用二八分析法进行引申,认为每个子空间内少数的特征真正决定了该场景空间内的绘制性能,那么当该子空间内少数特征的变量重要性比例总和达到整体特征的多数水平时,则进一步关注这些少数特征并从中分析子空间内的性能瓶颈。另外,划分后子空间的数据样本个数需要满足大于某一最小阈值的条件,其目的是当计算子空间内的变量重要性时保证存在OOB数据。 本文针对融合了多种绘制算法的复杂场景,实现的基于空间划分的瓶颈分析方法流程如图2所示。 本文以宫殿模型为基础场景,融合了基于光源链表(Light Linked List,LLL)的实时光照算法,实现了场景内部多光源的实时动态变化。同时,本文结合了顺序无关的半透明(Order-Independent Transparency,OIT)渲染技术以及屏幕空间环境光遮蔽(Screen-Space Ambi⁃entOcclusion,SSAO)渲染技术,实现了较好的透明物体绘制效果及全局光照效果。本文所有实验数据均来自于以下场景,如图所示: 图2 算法流程图 图3 LLL 图4 OIT 图5 SSAO 本文设计了宫殿场景内不同的漫游路径,记录了漫游过程中每一帧的相机信息、透明物体片元个数、光源半径、光源个数、SSAO采样半径、SSAO模糊半径及光源位置信息。将场景漫游后记录下的所有信息进行数据处理,最终得到以下特征如表1所示。 本文根据不同的场景漫游路径生成多组实验数据,通过基于空间划分的瓶颈分析模型得到以下几组不同的效果图: 表1 图6 图7 图8 图9 图6-图9分别展示了漫游数据被划分成2~6个场景子空间的效果。图6中两个子空间的性能瓶颈因素从左至右分别为光源个数和透明物体片元个数;图7中三个子空间的性能瓶颈因素从左至右分别为SSAO采样半径、光源个数和透明物体片元个数;图8中四个子空间的性能瓶颈因素从左至右分别为SSAO采样半径、光源个数、透明物体片元个数和SSAO模糊半径;图9中六个子空间的性能瓶颈因素从左至右且从上至下分别为SSAO采样半径、光源个数、光源半径、光源个数、透明物体片元个数和SSAO模糊半径。从以上结果可以看出,经过划分后的空间均有着各自不同的影响场景绘制性能的瓶颈因素。 针对融合多绘制算法的复杂场景性能瓶颈分析问题,本文提出了基于随机森林变量重要性度量的空间划分方法,将复杂场景细分成不同的子空间,通过结合子空间内相关的绘制算法定位影响绘制效率的瓶颈因素,从而对复杂场景的绘制性能提出指导性的改进方案。但是本文利用随机森林算法作为基本工具,其算法的随机性会导致瓶颈分析模型存在不稳定的问题。未来的工作会进一步优化瓶颈分析过程,让整体模型趋于稳定。 参考文献: [1]Breiman L.Random Forests[J].Machine Learning,2001,45(1):5-32. [2]Breiman L.Out-of-Bag Estimation[OE/OL].1996.ftp.stat.berkey.edu/pub/users/breiman/OOBestimation.ps. [3]Verikas A,Gelzinis A,Bacauskiene M.Mining Datawith Random Forests:A Survey and Results of New Tests[J].Pattern Recognition,2011,44:330-349. [4]Abdul Bezrati.Real-Time Lighting Via Light Linked List[M].GPUPro 6,2016:183-193. [5]Luna F.D.Introduction to 3DGame Programming with Directx11[M].Mercury Learning&Information,2012.
1.2 变量重要性

2 算法描述
2.1 空间划分


2.2 划分终止条件
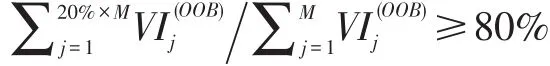
2.3 算法步骤
3 实验结果
3.1 实验数据




3.2 实验结果





4 结语
