基于动物集群行为的无人机群目标围捕策略
2018-04-24陈志鹏李健
陈志鹏,李健
(四川大学电子信息学院,成都 610065)
0 引言
多无人机协同控制是这几年的研究热点,而分布式是其中的研究偏向,相较于集中式控制,分布式要求各个无人机等价,拥有相同的功能,不需要集中控制。生态系统中,每个动物是单独的个体,动物个体行为相对简单,集合成群后往往能表现出复杂的行为,完成复杂的任务。随着无人机技术的发展,单个无人机的执行任务能力、可靠性、效率等都有很大提高,但遇到复杂的,需要高效率的,对空间分布有要求的任务时,往往难以胜任,此时只有通过多个无人机合作才能完成。本文提出基于鱼群的多无人机目标围捕策略方法,通过多无人机围捕考察多无人机鲁棒性,同时无人机目标围捕也是目前无人机群发展的研究主题之一。
在没有目标或没有检测到目标的环境下,无人机群遵循集群行为的三原则模型——Biod模型,在仿真中体现集群行为的实际情况:向邻居中心靠拢,尽量与邻居方向一致,尽量避免碰撞。仅仅依靠三原则模型,可能会使无人机陷入局部最优,分散为多个无人机小群体,为了避免该情况发生,使每个个体向群体中心靠拢,这里我们在Biod模型的基础上加入内聚性。
在有目标或检测到目标的环境下,无人机群采取目标围捕策略。付勇、汪浩杰设计了围捕机器人速度小于目标点速度的围捕策略,但该情况只有目标进入机器人包围圈时围捕成功率才得到提高[2]。裴惠琴、陈世明、孙红伟提出可扩展移动机器人群体的围捕控制[3],核心是用数量优势弥补速度劣势,而且假定围捕目标是直线运动,不适用于本文提出的随机运动的情况。本文提出一种基于势点的协作包围策略,在目标点周围建立围捕势点,每架无人机占据一个势点,然后收缩包围圈。最终形成围捕,使目标点无法移动或者速度明显降低而无法逃脱包围圈。
若目标点包含逃逸策略,设置目标点的感知半径为R,当目标点感知到围捕无人机时,会朝着反方向逃逸,若围捕无人机没有速度上的优势,则围捕成功率会大大降低。为了提高该情况下的围捕成功率,需要进行拦截围捕。王斐、魏巍、吴成东采取相关路径规划方法对目标进行实时跟踪[4],但这只是沿着目标轨迹被动跟踪,并没进行拦截围捕,当追捕目标有逃逸策略时,围捕成功率会降低。因此,很多研究者采用轨迹预测模型,围捕机器人除了追捕任务,部分拦截机器人直接向预测位置移动,提高了围捕成功率。如有采用卡尔曼滤波方法实现了目标预测跟踪[5]、神经元预测法[6]、方法运算复杂,收敛速度慢,不适用于高动态的无人机网络。本文使用最小二乘预测法,对目标轨迹进行采样并通过预测方程预测目标未来位置,虽然精度没有前两个那么高,但是有运算速度快的优点,而且对于目标的预测,并不需要太高的精度,只需达到对目标行进路线的探知并提前分布好无人机进行拦截,这样就能把围捕区域控制在理想区域内。
1 任务描述
本文采用的场景是多对单的无人机围捕场景。围捕任务分为搜索、预测、包围/拦截、缩小包围、捕获,在二维受限制的场景中,围捕无人机和目标点一开始设置为随机运动,围捕无人机半径r1,数量N,目标半径r2,目标点感知半径R2,也称之为安全距离,在围捕过程中,围捕半径R应该大于该安全距离,防止目标点侦测到威胁而逃逸。在形成包围圈后,再缩小围捕半径R,目标点无法逃逸或者移速明显降低则视为围捕成功。
2 最小二乘法轨迹预测的目标围捕
当有N架围捕无人机时,则在目标点周围建立N个势点,N/2作为追捕势点,N/2作为拦截势点,每架无人机占据一个势点,则追捕势点的坐标表示为:

(xe,ye)为目标点坐标,(xi,yi),{i=1,2,3..,N/2}为追捕势点集合。拦截势点表示为:

(xc,yc)为t时刻后预测的目标点坐标,(xi,yi),{i=N/2+1,N/2+2…,N}为拦截势点集合。
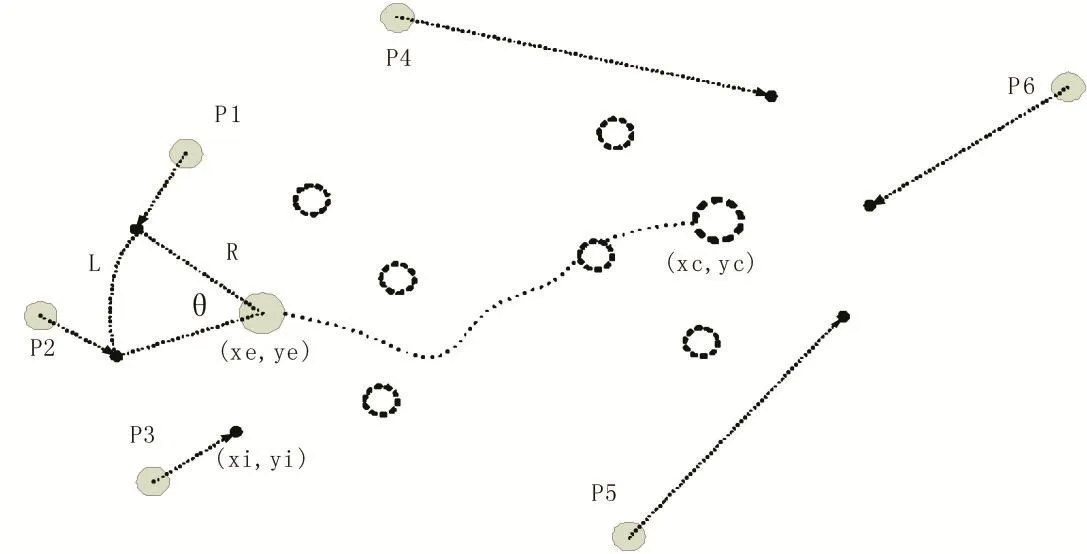
如果围捕机器人都从同一侧进行目标追捕时,若无人机速度V1小于目标速度V2,则很容易让目标点往相反方向逃脱,所以至少达到两面拦截,这样才体现无人机群的合作策略。如图1,有6个无人机对目标点进行围捕,用P{P1,P2,…,P6}表示围捕无人机的集合,P1,P2,P3进行跟踪围捕,P4,P5,P6进行拦截围捕。
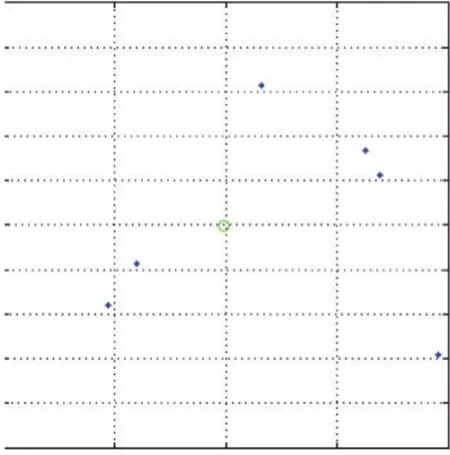
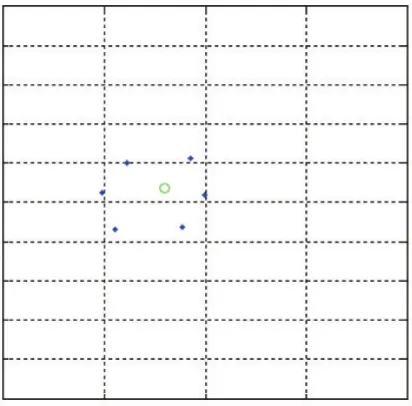
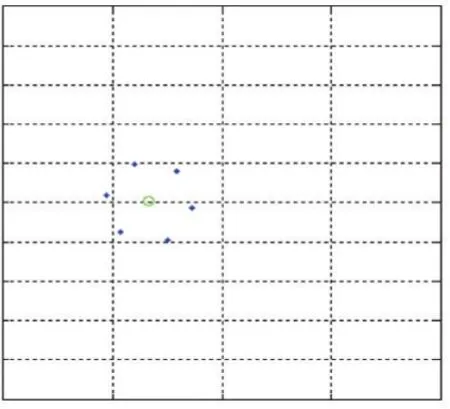
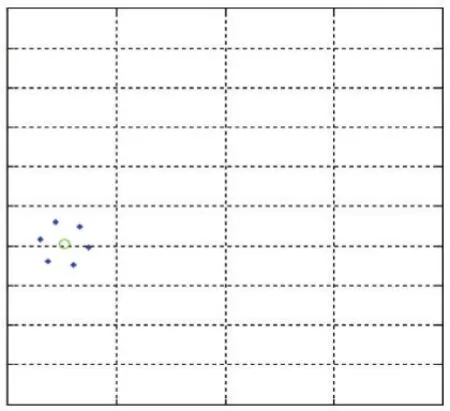
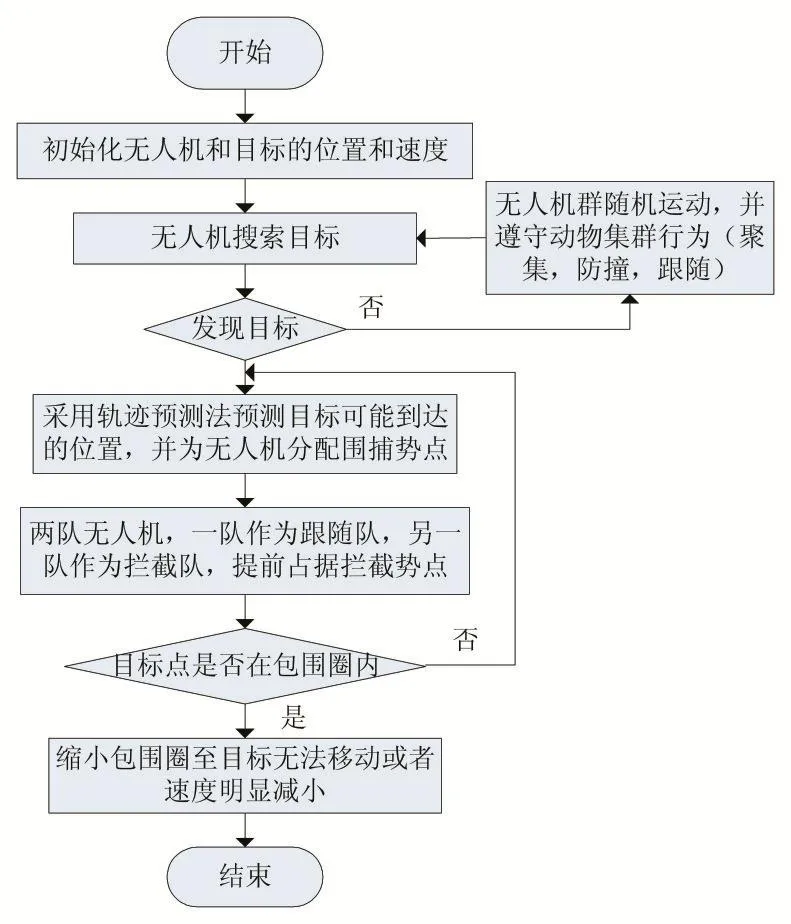
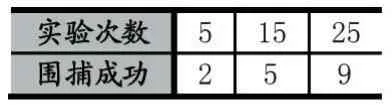
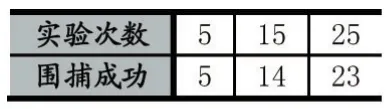
最小二乘法是一种经典的曲线拟合方法,相较于卡尔曼滤波方法和神经元法,它有收敛速度快的优点,这里我们利用最小二乘法进行目标轨迹曲线的拟合,从而预测目标下一刻的位置。这里每隔t1时刻记录一次目标轨迹上的坐标,记录k个相异的坐标点(x1,y1),(x2,y2),…,(xk,yk),每当记录一个新的坐标点 k+1,则丢弃最旧的点,则可以实现最新的动态预测。求一个m 次多项式 P(x)(k 求出系数a0,a1,…,ak,由a0,a1,…,ak来预测目标在未来时刻n的位置yk+n=P( )xk+n。n的取值过小者达不到预测效果,如果太大预测准度不高,需通过经验确定n值的大小。 当目标处于包围圈中时,围捕无人机收缩围捕半径R,如图1所示,当有6架围捕无人机,则围捕角度,目标半径r2,无人机半径r1,若要使目标无法逃脱,应有L<2(r1+r2),又由圆的半径和弧度的关系有所以为了防止目标逃脱形成有效围捕,包围半径至少收缩到不同的无人机数量,动态的调整围捕半径,或者根据围捕半径,计算出形成有效围捕需要多少架无人机。 图1 目标预测的追捕拦截策略 如图2所示,当无人机群没有发现目标点的时候,按照动物集群原则进行群体移动,在仿真环境中,为了更好观察和体现基于动物群体的集群行为,我们适当增加无人机数量。当目标点出现时,则分配一定的无人机完成目标围捕任务,为保证有效围捕,围捕半径R应该设置比目标的感知半径R2大。 图2 无人机群目标围捕策略流程图 为了验证本文提出围捕策略的有效性,本文在Windows10环境下采用MATLAB进行仿真实验。 仿真在200×200的无障碍环境中有6架无人机和一个围捕目标,无人机速度设为1m/s,目标点速度3m/s,图3是t=0时的初始状态,机群检测到目标点,图4是t=100s,两拨机群形成围捕拦截状态,当目标点在包围圈时,防止目标逃脱,机群收缩包围圈至围捕半径为表1和表2对有无采用预测轨迹的拦截围捕策略进行目标围捕成功率进行比较,现在在没有数量优势和速度优势的条件下,只有基本追捕策略条件的围捕成功率只有30%,只有围捕无人机群的初始坐标位置大致分布在目标点的四周时,才有可能捕获目标。 表1 基本群体捕食策略实验结果 表2 最小二乘法拦截/围捕策略实验结果 本文提出基于动物集群行为的无人机群目标围捕策略,无人机除了具有类似生物群体的群体行为,还从中加入了基于势点的围捕策略,在安全距离外对目标形成包围圈,最终收缩包围圈捕捉目标点。为了提高围捕成功率,本文加入基于最小二乘法的预测模型,使一小队无人机在目标点的前进方向上进行拦截,提高了围捕成功率。 图3 初始状态 图4 围捕/拦截 图5 形成包围圈 图6 缩小包围圈 参考文献: [1]段海滨,李沛.基于生物群集行为的无人机集群控制[J].科技导报,2017,35(7):17-25. [2]付勇,汪浩杰.一种多机器人围捕策略[J].华中科技大学学报,2008,36(2):26-29. [3]裴惠琴,陈世明,孙红伟.动态环境下可扩展移动机器人群体的围捕控制[J].信息与控制,2009,38(4):437-443. [4]王斐,魏巍,吴成东.未知环境下的多移动机器人协作围捕[A].中国控制与决策会议论文集[C].东北大学出版社,2009:3024-3029 [5]Chi-Yi Tsai,Kai-Tai Song,Dutoit,X,etal.Robust Mobile Robot Visual Tracking Control System Using Self-Tuning Kalman Filter[A].International Symposium on Computational Intelligence in Robotics and Automation[C].Jacksonville,FL,USA,IEEE Computer Society Press.2007.161-166. [6]Dongbing Gu,Huosheng Hu.Neural Predictive Control for a Car-Like Mobile Robot[J].International Journal of Robotics and Autonomous Systems,2002,39(2-3):1-15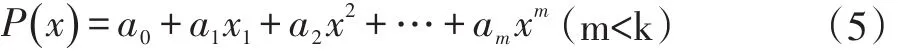
3 围捕算法流程
4 仿真实验
5 结语