基于高斯径向基函数网络的潜在剖面建模方法

黎鸣

（四川大学计算机学院，成都 610065)

1 潜在剖面分析

近年来，潜在变量建模（潜在结构分析，Latent Vari⁃able Modeling，Latent Structural Analysis）越来越受到医学生物、社会心理等学科的重视，其原因在于，一方面，它能通过潜在变量的概念来表示外显变量（因变量）所蕴含的抽象且无法直接观察的内部关系，另一方面，传统的显变量分析方法的有效性正逐渐受到数据复杂性的影响，研究者搜集到的数据越来越底层、复杂、交错、实时，这些数据的潜在关系很难再通过简单的转换方法得到。而潜在剖面分析（LPA）作为一种对内部因素间交互进行建模的方法，其有效性在医学生物、社会心理等学科领域已经得到大量的证实。LPA是一种以人为中心的潜在变量建模方法，其基本假设在于因变量间存在有意义的、共同的模式（Pattern），而这种假设与类型学（Typology）等多个研究领域所用的假设相仿[1]。由于其假设也包含了因变量间存在的结构化关系，因此，LPA也被作为一种结构化（Structural）的建模方法。

按照外显变量与潜在变量的数据类型（连续或离散），潜在结构分析可以分为四类，即：外显离散且潜在离散的潜在类别分析（Latent Class Analysis），外显连续但潜在离散的潜在剖面分析（Latent Profile Analysis），外显离散但潜在连续的潜在特质分析（Latent Trait Analysis），以及外显连续且潜在连续的因素分析（Fac⁃tor Analysis）[2]。可以说，潜在结构分析是传统因素分析的发展与扩展，与传统因素分析一同建立了一个完整的潜在分析方法框架。

潜在类别分析（LCA）与潜在剖面分析（LPA）都是基于贝叶斯统计理论的一种，LCA为无参估计，LPA为有参估计，都采用了“属性条件独立性假设”（Attribute Conditional Independence Assumption），即对已知的显变量，假设所有属性相互独立。对于一个具有M个属性、K个潜变量的LCA的模型，其贝叶斯判别公式如公式

由于LPA与LCA的区别主要在外显变量是否连续这一点上，因此，当外显变量为连续的时候，贝叶斯决策假设外显变量服从于多个同构的潜在分布，通常假设该分布为正态分布。因此，属于潜在类别k并且具有显变量模式x的联合概率密度函数p可以表示成公式（2）的形式[3-4]：

其中，p是服从均值μ、协方差阵为Σ的正态分布的概率密度函数，各个潜在分布通常假设均值为0，协方差可以相同也可以不相同。ηk为潜在类别概率（La⁃tent Class Probability），即为前文所述的先验概率；这时候的被称为类条件概率密度（Class-Condi⁃tional Probability Density）。不同于LCA的无参估计过程，LPA通常采用基于期望最大化（EM）的最大似然法（MLE）估计假设分布的参数，由于LPA通常仅需要得到估计的分布参数，因此，在LPA应用领域又通常将该模型称为贝叶斯回归模型或贝叶斯聚类模型[5]。由于在现实问题中，属性条件独立性假设通常很难成立，通过对属性条件独立性假设进行放宽，由此可以得到一类称为“半朴素贝叶斯分类器”（Semi-Naïve Bayes Clas⁃sifier）的学习方法，该类方法可以建模显变量属性间的关系。也可以通过建立贝叶斯网络（信念网，Bayesian Network，Belief Network），借助有向无环图来刻画属性间的关系[6]。

LPA基于贝叶斯分类器的原理，同样获得了很好的显变量分类（聚类）能力。虽然LPA解决了从显变量（因变量）到潜变量的转化过程，但是，大部分研究仍然希望得到的是自变量与显变量之间的关系。为此，通常做法是直接使用现有的分类方法建立自变量与潜变量之间的分类模型，藉由潜变量模型得到显变量结果。这种两段式的训练方式，找到的都是局部最优的模型，而不是自变量（特征）与显变量之间关系的最优模型，因此，通常由此推断的自变量与显变量之间的解释度（拟合优度）都很低，现有文献都规避自变量与显变量之间的关系，而提出以“人”（潜变量）为中心的判别方式，忽视了模型的最终应用目的。

2 径向基函数网络

径向基函数（RBF）网络（Radial Basis Function Net⁃work）是一种以径向基函数为隐藏层神经元节点的前馈神经网络，是一种连接主义的模型。神经网络的有效性在神经科学领域和计算机领域均得到了大量的证明，它由具有适应性的简单单元组成广泛并联的网络，是对生物神经系统的模拟，而前馈神经网络（层间全连，层内不连）是最基本的一种神经网络结构[6]。RBF网络是一种非线性局部逼近网络，能逼近任意的非线性函数，具有良好的泛化能力，同时，仍具有较好的解释性。其网络结构通常图1所示：

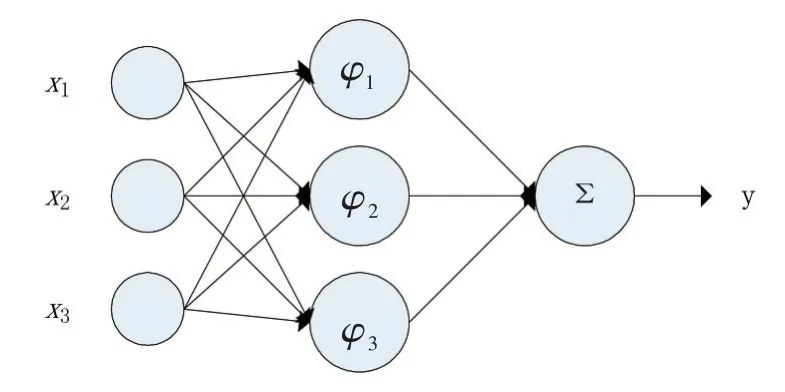
图1 RBF网络结构

其中x为输入向量，xi为第i个属性（特征），x所在的神经元节点为输入层；φ为高斯径向基函数，其公式可以定义为公式Eq.3的形式，φ所在的神经元节点为隐藏层，φj为第j个神经元的高斯径向基函数；Σ为求和函数，Σ所在的神经元节点为输出层；y为网络的输出。

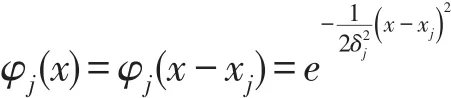
RBF网络可以理解为：输入层是网络与外界环境的连接，隐藏层是输入空间到隐藏空间之间的变换，输出层是网络的响应。高斯函数φ在统计学文献中广泛的解释为核（Kernel），因此RBF网络是一种类似于核回归的核方法（模型）[7]。该网络的训练方式通常采用两段训练（2-Stage Training）的方式：第一阶段，使用非监督（Unsupervised）学习的训练方式寻找高斯径向基的中心样本，第二阶段，使用监督（Supervised）学习的训练方式训练网络参数。

RBF网路与LPA方法具有极高的相似性，从LPA的方向解释，x即为自变量（特征），φ为潜变量的概率密度函数，y为显变量，将Σ替换为采样函数，则该网络即为RBF-LPA网络。其训练方式也采用两段训练的方式，第一阶段，使用LPA朴素贝叶斯回归的方法，确定高斯径向基的概率参数，第二阶段，使用传统的BP方法训练整个网路的参数。

3 结语

本文给出了一种基于RBF的LPA方法，该方法综合考虑了如何将LPA直接用于全局建模。虽然该思想结合了LPA易解释，RBF效果好的优点，但是，后续需要更多实际的应用来证明该方法的有效性，以及从定义上给予更严格的证明。

参考文献：

[1]Ferguson S,Hull D.Personality Profiles:Using Latent Profile Analysis to Model Personality Typologies[J].Personality&Individual Differences,2018,122:177-183.

[2]邱皓政.潜在类别模型的原理与技术[M].北京大学出版社,2008.

[3]RichardO.Duda,PeterE.Hart,DavidG.Stork.模式分类[M].机械工业出版社,2003.

[4]孙即祥.现代模式识别[M].国防科技大学出版社,2002.

[5]赵丽,李丽霞,周舒冬,等.潜在剖面分析和系统聚类法比较的模拟研究[J].广东药学院学报,2013,29(2):206-209.

[6]周志华.机器学习[M].清华大学出版社,2016.

[7]SimonHaykin,海金,Haykin.神经网络与机器学习[M].机械工业出版社,2009.