基于分布式MWC的全盲协作频谱感知方法的研究
2018-04-24郑广春张弘李智
郑广春,张弘,李智
(四川大学电子信息学院,成都 610065)
0 引言
随着无线电通信等领域信号频率和带宽的不断提高,使得以奈奎斯特理论为指导的传统采样方法面临着采样率过高的巨大压力,信号采样已成为制约数字信号处理系统发展的一个瓶颈,ADC采样率的提高不仅增加了硬件的成本,同时也增加了数据处理的难度。2006年,由Donoho与Candes等[1]人提出的压缩感知(Compressed Sensing,CS)理论是一个充分利用信号稀疏性或可压缩性的全新信号采集、编解码理论。该理论表明,当信号具有稀疏性或可压缩性时,通过采集少量信号投影值就可以实现信号的准确或近似重构。2010年麻省理工学院的Y.C.Eldar教授及其研究团队在随机解调模型和多倍集采样体系的基础上,发展出了一种基于多通道随机混频的模拟信号欠采样体系——调制宽带转换器(Modulated Wideband Converter,MWC)[2]。2011年该研究团队把MWC应用到宽带频谱感知[3],采用低配置的ADC和DSP实现了对宽带频谱的精确、实时感知。2012年该团队把MWC应用到CR中的循环平稳特征检测[4],利用欠采样序列实现了对目标信号循环平稳特征的精确检测。2016年,学者徐自勇在文献[5]中首次提出分布式调制宽带转换器的思想,作者将DMWC(Distributed Modulation Broadband Converter)中每一个通道作为一个感知节点分布在源信号的周围,各感知节点协同感知,通过一个数据收集中心把所有感知节点的欠采样数据汇总、处理、做出统一的感知判决,从而计算出原始信号的支撑集。DMWC相对于MWC的唯一区别在于每个欠采样通道的输入信号不再完全相等,相互之间存在路径传输衰减。在衰减不大的时候,DMWC方法中常用OMP算法能够较准确地计算出源信号的支撑集。但是OMP算法在计算源信号支撑集的时候需要源信号的稀疏度和最大子带宽,然而在实际的宽频段多窄带信号感知问题中,信号的稀疏度和最大子带宽都是未知的,因此这使得DMWC在应用上存在一定局限性。为解决这一局限性本文在DMWC方法中引入信号稀疏度自适应匹配追踪算法(SAMP)。
1 调制宽带转换器的采样原理
1.1 建立系统模型
DMWC与MWC的主要区别在于DMWC的每个通道作为独立的一个感知节点分布在不同的区域,由于各节点与源信号的距离不同,所以各节点之间存在信号的传输衰减;DMWC全盲协作频谱感知网络(FBCSSN)的模型由如图1所示:
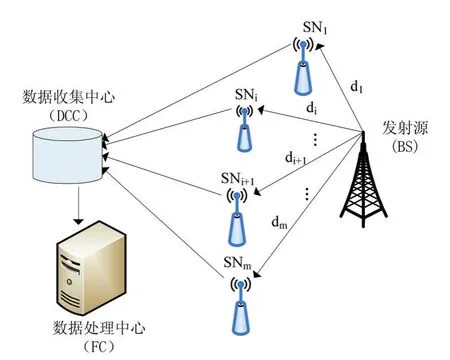
图1 DMWC全盲协作频谱感知网络
该模型主要包括四个部分:发射基站(BS),多个感知节点(SN),数据收集中心(DCC),数据处理中心(FC);其中发射基站到每个传感节点间的距离记做di(i=1,2,3,…,m)。由于各感知节点分布的位置不同,各感知节点到源信号的发射基站的距离也就不同,因而信号在传输过程中必定会产生一定的衰减,传输距离的不同导致衰减的程度也不同,传输衰减因子可以同公式(1)计算得到;

其中Pa是接收功率,Pt是发射功率,G是系统增益,F表示系统损耗因子[6]。显然,衰减因子θ越小,表示信号传输过程中衰减越大。数据收集中心主要收集各个感知节点采样所得到的数据,数据处理中心将利用数据收集中心收集的数据来计算源信号的支撑集。
1.2 分布式调制宽带转换器理论
DMWC是在MWC理论基础上提出的新的理论方法。其结构框图如图2(a)所示。
如图2所示,x(t)为发射源信号,pi(t)为周期伪随机序列,h(t)为截止频率为的低通滤波器;DMWC中m个通道彼此分离,每个通道等同于一个感知节点,各个感知节点相对于发射源的距离不同(如图1所示),由公式(1)可计算各感知节点经过不同的传输路径后信号的不同衰减度。这里我们假设信号的衰减度为θi∈(0,1],1≤i≤m,由于存在传输路径的问题,那么每个感知节点接收到的信号实则为θix(t),当θi的值很小(接近0)时,噪声功率将大于感知节点所接收到的信号功率,源信号将被淹没在噪声中;当θi的值接近1时,表示该通道没有传输损耗,这在理论上等同于MWC。感知节点所接收到的信号θix(t)与伪随机序列pi(t)卷积混频,混频的实质则为频谱的搬移,如图3所示,经过多次频谱的搬移,宽频带内的多个子频带将被搬移到低频带上,低频带上的叠加频谱包含了整个宽频带内的所有频谱信息;然后混频器的输出通过截止频率为的低通滤波器h(t)。的速率进行采样得到采样序列yi[n]。每个ADC通道输出序列yi[n]的离散时间傅里叶变换Yi(ej2πfTs)与x(t)的傅里叶变换X(f)之间的关系满足等式:
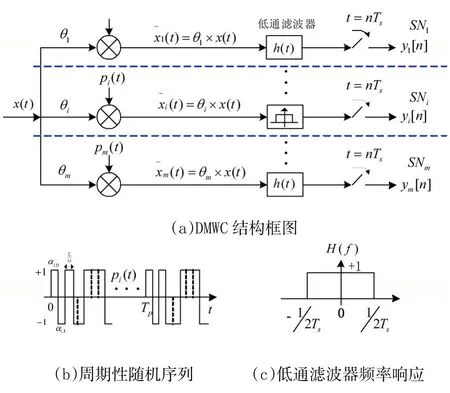
图2 DMWC主要参数
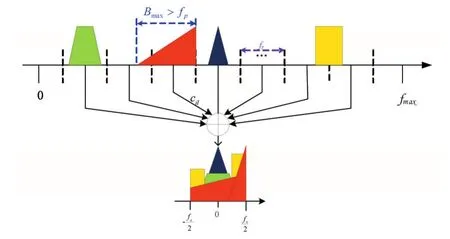
图3 频谱搬移示意图

滤波器的输出端接ADC模块,并且以
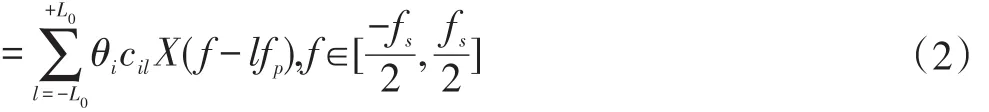
式(2)可用矩阵的形式表示为:

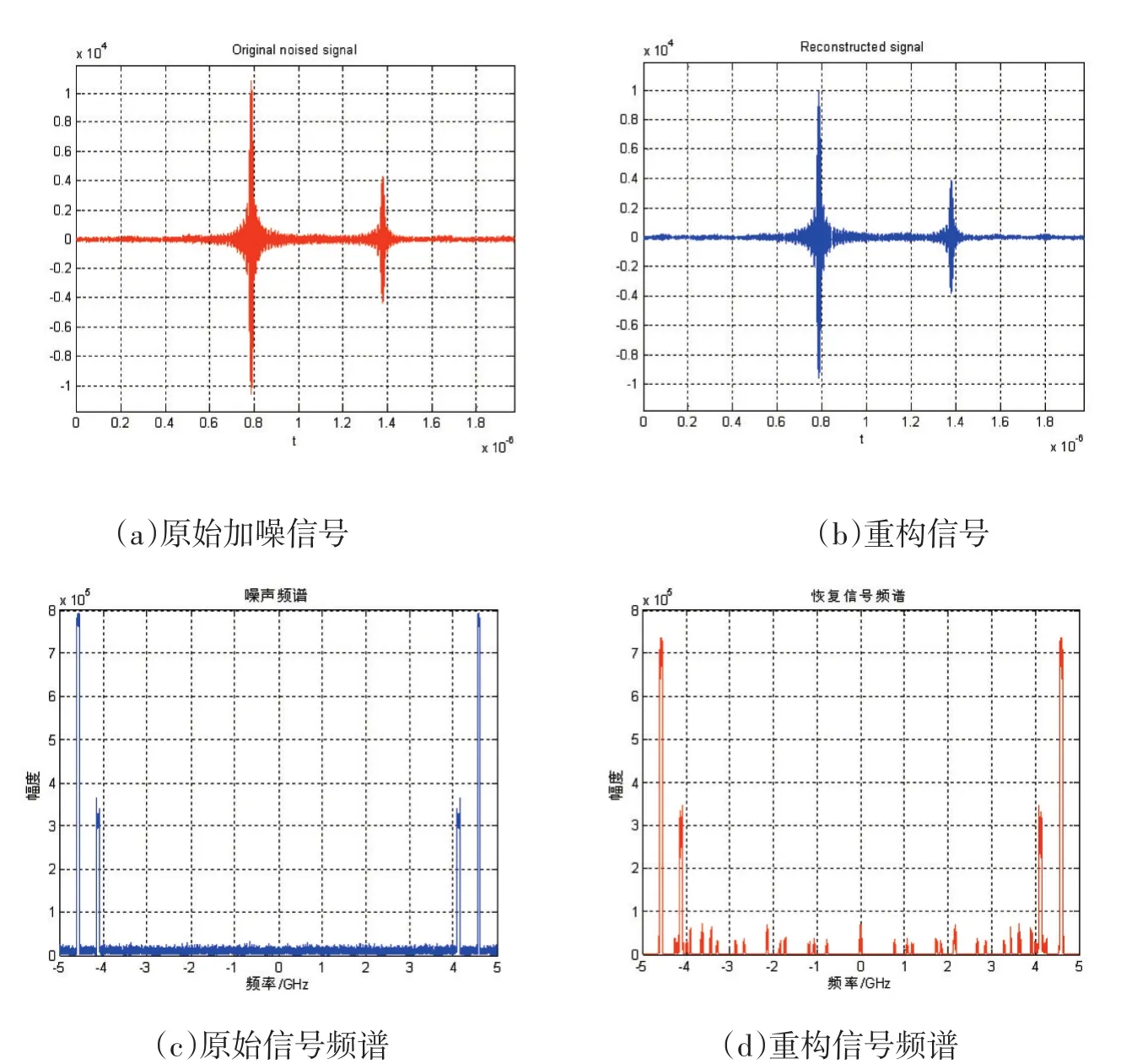
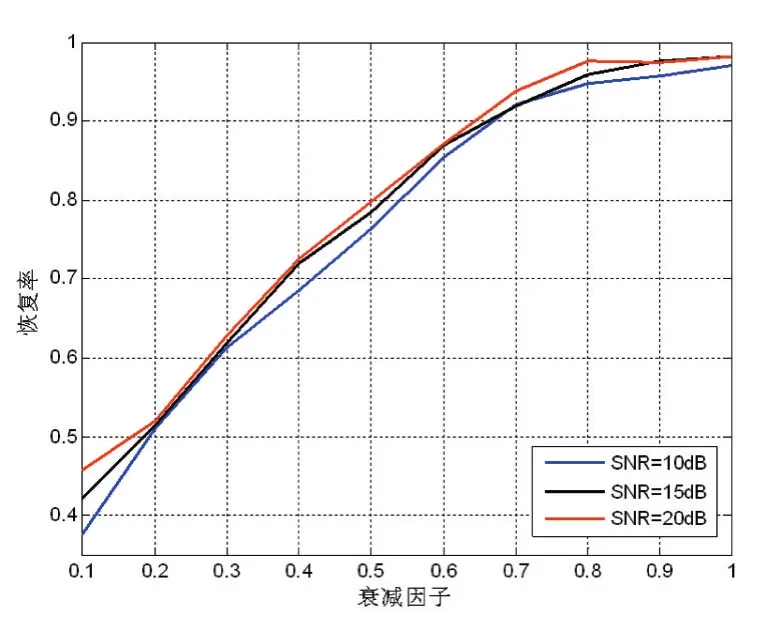
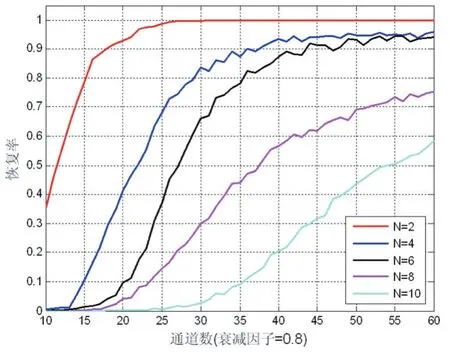
y(f)是m×1维向量,第i个元素为,矩阵A是m×L维矩阵 (m 伪随机序列的长度M=L=2L0+1其中,频谱搬移的步长,l为频谱搬移的步数。 DMWC中OMP算法准确地计算出源信号支撑集的条件是已知源信号的稀疏度和子带的最大带宽;如果不知道源信号的稀疏度和子带最大带宽时,则容易出现对稀疏度过估计或者欠估计,导致无法准确计算出源信号的支撑集而重构失败。然而实际感知宽频段多窄带信号时,稀疏度和子带最大带宽都是无法准确预知的,所以引入无需频带数和子带最大宽度为先验知识的SAMP算法作为DMWC支撑集恢复算法,该算法的引入使得DMWC得到更广泛的应用。 SAMP重构算法的算法流程如下: 输出:支撑集F, (1)初始化残差r0=v,支撑集F0=∅,步长L=S,迭代次数t=1; (2)计算余项与测量矩阵各列的相关性u=,选择u中L个最大值,将这些值对应A的序列号j构成集合Sk; (3)更新选取的A的列序号:令Ck=Ft-1⋃Sk,表示矩阵A的第j列,从A中选择对应的列组成新的矩阵At; (4)求v=AtKt的最小二乘解, (7)①如果残差rnew=0则停止迭代进入第(8)步;②如果,更新步长L=L+S返回第(2)步继续迭代;③如果①②两个条件都不满足,则F=Λt,rt=rnew,t=t+1,如果t≤M停止迭代进入第(8),否则返回第(2)步继续迭代; (8)输出稀疏度估计值K^tL和支撑集F。 为了验证DMWC的全盲协作频谱感知系统的有效性,我们模拟产生频谱稀疏信号: 其中Ei,Bi,fi,τi,N分别表示i个子频带的能量系数、带宽、载波频率、时间延时和子频带数。这里我们假设,N=4,Ei=[1.251.79],Bi∈[30MHz80MHz],fi∈(-fnyq/2fnyq/2),τi=[0.40.7],随机序列长度M=195,通道数m=50,由MWC理论可知频谱搬移的步长fp=fnyq/M=51.28MHz,即奈奎斯特率为fnyq的信号被切成若干长度为fp的频谱切片。 DMWC中OMP算法能够准确计算支撑集的条件是知道原始信号的频带数N和子带最大带宽,然而实际在解决宽频段多窄带信号问题中,子频带的带宽和频带数都是不确定的,这些苛刻的条件就限制了DMWC在实际中的应用。在仿真中我们假设Bi∈[30MHz80MHz],这样fp与Bmax的大小关系就随机的,在本文中我们引入稀疏度自适应匹配追踪算法(SAMP)来计算支撑集,SAMP算法在计算支撑集的过程中不需要知道先验知识N和Bmax,图4给出了当N=4,衰减因子θi=0.8,SNR=15dB时,在SAMP算法下DMWC恢复时域、频域波形对比结果图。 图4表明,在SNR=15dB时,即使通道传输过程中存在一定的衰减,DMWC全盲协作频谱感知系统仍然能够很好地恢复出原始信号的频谱。 图4 DMWC系统信号重构结果 (1)衰减因子θi=0.8时,恢复率与信噪比的关系如图5。 从上图可以看出,当SNR=10dB时,恢复率高达90%,随着信噪比的提高恢复率也在不断提高。实验证明了即使信号在传输过程中存在一定程度的衰减,在可观的性噪比下仍能够得到很高概率的恢复。然而不同节点的位置不同导致信号的传输路径也就不同,因此传输过程中信号的衰减程度也就不同,下面我们需要验证不同衰减下,信号的恢复率。 (2)不同信噪比下,恢复率与衰减因子的关系图6。 图6 衰减因子在不同信噪比下与恢复率之间的关系 从上图可知在信噪比一定的情况下,恢复率随衰减因子的增加而提高,当θi=1时,即认为信号在传输过程中没有衰减,此时恢复率达98%;当衰减因子很小时(θi=1),恢复率低于45%;上图还表明了在衰减因子不同的情况下,信噪比与恢复率的关系,很明显,随着信噪比的增加恢复率也有相应的提高。 图7 不同子带下恢复率随通道的变化关系 图7给出了θi=0.8,SNR=15dB信时不同稀疏信号随通道数的关系;当通道数一定时,信号越稀疏,恢复率越高;当子频带数N=2时,通道数为25时恢复率接近100%;当子频带数N=4时,通道数为40时恢复率接近95%;当子频带数N=6时,通道数为50时恢复率接近95%;当子频带数为8或10时,通道数为60时恢复率仍低于80%;说明随着子带个数越多,需要越多的通道数来匹配。在实际应用中可以通过调节DMWC的通道个数(感知节点个数)来匹配信号稀疏度,使得支撑集的恢复更准确。 本文基于DMWC方法中OMP算法在实际应用中的缺陷,我们引入稀疏度自适应算法(SAMP),SAMP算法与DMWC方法的完美结合不仅充分考虑到实际信号在传输过程中存在衰减问题,还能在未知源信号的稀疏度和最大子带宽度的情况高概率的恢复源信号的支撑集。大量实验证明DMWC方法与SAMP算法结合不仅能够快速、准确地恢复宽带稀疏信号的频谱,而且能够灵活地匹配信号稀疏度与通道之间的关系,使得DMWC理论的应用前景更广阔。 参考文献: [1]Donoho D L.Compressed Sensing[J].IEEE Transactions on Information Theory,2012,52(4):1289-1306. [2]Mishali M,Eldar Y C.From Theory to Practice:Sub-Nyquist Sampling of Sparse Wideband Analog Signals[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(2):375-391. [3]Mishali M,Eldar Y C.Wideband Spectrum Sensing at Sub-Nyquist Rates[J].IEEE Signal Processing Magazine,2010,28(4):102-135. [4]Tian Z,Tafesse Y,Sadler B M.Cyclic Feature Detection With Sub-Nyquist Sampling for Wideband Spectrum Sensing[J].IEEE Journal of Selected Topics in Signal Processing,2012,6(1):58-69. [5]Xu Z,Li Z,Li J.Broadband Cooperative Spectrum Sensing Based on Distributed Modulated Wideband Converter:[J].Sensors,2016,16(10). [6]Rappaport T S.Wireless Communications:Principles and Practice",Upper Saddle River,NJ:Prentice-Hall[J].Horwood Publishing Limited Chichester,2002. [7]盖建新.基于MWC的稀疏宽带信号亚奈奎斯特采样技术研究[D].哈尔滨工业大学,2013. [8]姚婷婷.基于MWC的模拟信息转换技术研究[D].哈尔滨工业大学,2015. [9]叶丰,罗景青,俞志富,等.基于欠采样的宽频段多窄带信号频谱盲恢复系统[J].电子测量与仪器学报,2011,25(11):959-965. [10]郑仕链,杨小牛.用于调制宽带转换器压缩频谱感知的重构失败判定方法[J].电子与信息学报,2015,37(1):236-240. [11]Israeli E,Tsiper S,Cohen D,et al.Hardware Calibration of the Modulated Wideband Converter[C].Global Communications Conference.IEEE,2015:948-953. [12]杨树树,宁勇.基于MWC压缩采样系统的通道失配校正研究[J].航天电子对抗,2015,31(3):37-39.
2 SAMP重构算法
3 仿真实验
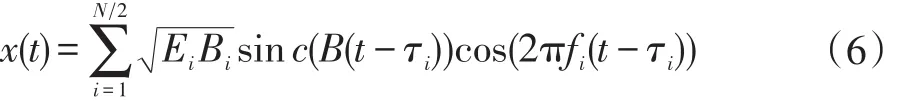
3.1 验证SAMP 算法恢复成功率与传输衰减θi 和信噪比的关系
3.2 验证不同稀疏度信号在SAMP 算法下恢复成功率与通道数的变化关系
4 结语
