基于Kharitonov理论的巡检机器人关节电机鲁棒控制

邵 嶽

（沈阳工业大学电气工程学院，沈阳 110870）

巡检机器人是一种沿高压架空输电线路行驶代替或者辅助人工巡检的特种电力作业机器人，在国民生产和日常生活中占有重要地位，应用前景非常广阔[1]。从控制的角度看，机器人的有效控制是保证正常巡检的前提，但是机器人存在多输入、多输出、强耦合、非线性等特征，使得在实际工程应用中从宏观上得到机器人完整精确模型很困难。因此本文分解机器人的控制体系结构，从微观层面入手，以机器人的关节电机为研究对象，建立其PID闭环控制系统数学模型。考虑到关节电机PID参数很容易因野外恶劣气象条件、高空风载扰动、高电压强电磁干扰、以及电机的电枢反应，电机本身温度变化时，关节主电路的电阻，电感都会变化，这些都会影响电机标称值的改变。此外电机长时间的运行它与传动机构在结合处会的磨擦损耗，电机所带负载发生变化以及机器人运行在不同工况等，这些都会影响电机参数。以上不确定性因素加大了机器人控制的难度，影响机器人机械臂控制的精度和稳定性。在某些极端情况下，可能引起机械臂与线路上绝缘子、悬垂线夹、防震锤等障碍物发生碰撞、干涉甚至从高压线上脱线，造成输电线和机器人的损坏和巨大经济损失。因此，在控制过程中必须根据系统的运行状态实时对机器人关节控制器的PID参数进行在线自适应调整，以确保在不确定性存在的情况下机器人在作业过程中依然保持较高的控制精度和较好的稳定性。目前相关文献已提出了基于滑模变结构理论[2]、模糊理论[3]、神经网络[4]、遗传算法[5]及其相结合的很多的 PID 智能控制方法[6]，但这些大都是在忽略不确定性因素和扰动的理想情况下进行的。HUANGYJ[7]、彭瑞[8]、徐峰[9]等人提出了基于区间多项式理论的参数不确定系统鲁棒控制方法，Ho M T[10]提出了基于H∞理论的鲁棒PID控制方法但被控对象大多数是针对工业控制系统而非机器人的关节电机。吕永健[11]、恒庆海[12]等针对被控对象的抗干扰能力提出了直流电机的 H∞鲁棒控制策略，但都只是单独的研究电机的鲁棒控制而没有联系到机器人。王鹏[13-14]等人在建立巡检机器人机械臂各类动作运动模型的基础上提出了基于 HJI不等式的架空输电线巡检机器人的鲁棒控制，赵浩泉[15]等人提出了基于混合灵敏度的水下机器人鲁棒控制研究，刘开周[16]等人提出了基于结构奇异值的水下机器人鲁棒控制研究，但这些都只是从宏观上对机器人的控制进行研究而没有具体到机器人各个关节的控制。因此，当前针对高压输电线路巡检机器人特别是从微观层面上分析关节电机鲁棒控制这方面的研究很少。1978年原苏联数学家卡里托诺夫提出了著名的Kharitonov定理，在处理参数不确定系统的鲁棒控制问题上取得了重大突破，基于此，本文将Kharitonov定理与关节电机的鲁棒控制结合起来，提出一种针对高压输电线巡检机器人关节电机参数不确定PID控制系统的鲁棒控制策略，其目的是控制机器人关节电机在存在不确定因素和扰动的情况下，稳定工作保持优秀的控制品质，为机器人正常巡检提供有力保障。

1 巡检机器人的控制体系结构和关节电机建模

1.1 巡检机器人的控制体系结构

根据巡检机器人控制体系结构特点，可将其分为作业规划、任务协调、动作执行3个层面，如图1所示。作业规划主要包括巡检和故障处理；任务协调主要包括线上行走、障碍物识别、越障等；动作执行主要包括机械臂的上升、下降、平移、旋转。对巡检机器人机械臂各类动作的控制本质，可归结为对各关节电机的控制，电机动作与反应直接决定了机器人在线上的运行状态和效果，因此关节电机控制的稳定性在巡检机器人的控制体系中占有至关重要的作用，其是巡检机器人正常工作的必要条件。

图1 巡检机器人控制体系结构

1.2 巡检机器人的关节电机建模

巡检机器人各个关节的运动的总和表现在巡检机器人本体的运动，而每一个关节的运动又表现为关节电机的转动。要对巡检机器人的关节电机实施有效控制，首先需建立其控制模型，本文以巡检机器人行走轮关节为例建立关节电机数学模型，机器人关节电机电路模型如图2所示。图2中，u为电枢电压，i为电枢电流，R为电枢电阻，L为电枢回路电感，E为反电动势，J为转轴转动惯量，w为转轴角速度，B为粘滞摩擦系数，ka、kb为与电机有关的常数。

图2 巡检机器人关节电机电路模型

对电枢回路列KVL微分方程可得

逆电动势为

将式（2）代入式（1）得

对转轴列转矩平衡方程可得

对式（3）取拉普拉斯变换得

对式（4）取拉普拉斯变换得

由式（5）、式（6）可得

由式（7）可得关节电机控制系统框图如图3所示。

图3 巡检机器人关节电机控制系统结构框图

由图（3）可求得关节电机的传递函数为

则G(s)可简写为二阶系统的标准形式：

本文以式（9）为被控对象，通过调节电机输入电压来控制电机输出的角度，再通过传动机构来控制机械臂的运动，最后通过反馈来调节输入形成关节电机闭环控制系统结构如图4所示。

图4 巡检机器人关节电机鲁棒控制系统结构图

在扰动d的作用下被控对象G(s)中参数P、Q、M在一定范围内摄动，为克服扰动的影响需设计电机的鲁棒PID控制器，控制的目标是要动态寻找一组合适的鲁棒PID控制参数，使得各关节电机在有扰动和参数不确定的情况下仍然能够协调稳定工作保持鲁棒镇定，进一步提高巡检机器人在作业过程中各类动作的稳定性、准确性和抗各类干扰的能力，实现巡检机器人的线上正常自主作业。

PID控制器的传递函数为

系统的闭环特征方程为

将式（9）、式（10）代入式（11）得

2 Kharitonov理论及巡检机器人关节电机鲁棒PID控制分析

式（13）中， Kp、 Ki、 Kd为PID控制器的控制参数，在有扰动的情况下需要动态调整，P、 Q*、M*是与电机有关的常数，理想情况下是不变的，但在机器人作业过程中各种因素使得P、 Q*、 M*难以精确测定，且鲁棒PID参数的在线调整也使得 Q*、M*会动态变化，因此式（13）巡检机器人关节电机模型闭环特征多项式是一个参数不确定的3阶多项式。此类问题适合用Kharitonov定理进行稳定性分析。以下将给出Kharitonov定理及其推广，并分别对机器人关节电机的鲁棒稳定性进行分析。

2.1 Kharitonov定理及关节电机鲁棒PID控制分析

巡检机器人关节电机PID控制系统鲁棒稳定充分条件的推导如下。

由劳斯判据可得三阶系统稳定条件为

Kharitonov定理要求多项式系数变化是相互独立的，系数变化在一个矩形内部区域，但实际机器人电机控制系统式（13）的系数还与PID参数有关，此时系数应在矩形对角线曲线之上，所以只要保证此区域的稳定就可以保证系统鲁棒稳定，但Kharitonov定理给出的确是全部矩形的稳定条件，基于上述分析可知Kharitonov定理参数的变化域包含了实际系统参数的变化域，因此满足Kharitonov所有参数多项式稳定则实际系统一定稳定，实际系统稳定只代表满足参数变化域矩形对角线上方的所有参数系统稳定，并不代表所有矩形区域参数系统稳定，即式（15）中的4个Kharitonov多项式稳定只是系统鲁棒稳定的充分条件。

2.2 盒子定理及关节电机鲁棒PID控制分析

广义Kharitonov定理又称盒子定理，它在Kharitonov定理的基础上提出了判定参数相关联多项式鲁棒稳定的充要条件，广义Kharitonov定理引入了Kharitonov顶点对象和边对象的概念。

1）巡检机器人关节电机PID控制系统鲁棒稳定必要条件的推导

Kharitonov顶点对象是由被控对象传递函数分子的4个Kharitonov多项式和分母的4个Kharitonov多项式的不同组合，共16个多项式的集合组成的。设被控对象的传递函数可表示为形如式（17）的分子分母多项式形式。

分子多项式 ()Ns的4个Kharitonov多项式记作

分母多项式 ()Ds的4个Kharitonov多项式记作

则 ()Gs的Kharitonov顶点对象可用式（18）来表示。

式（18）中 Ni(s)(i =1、2、3、4) 为

将式（18）、式（10）代入式（11），可得闭环系统Kharitonov顶点对象特征方程式为

则闭环系统Kharitonov顶点对象特征多项式为

则理论上闭环系统的16个Kharitonov顶点对象特征多项式可简化为式（24）的4个多项式。

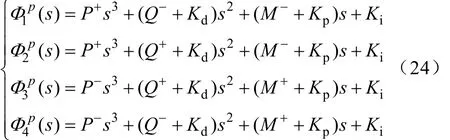
式（24）中的4个多项式都是确定系数的线性系统，可利用劳斯判据直接判定其稳定性求出参数的取值范围。因为系统稳定的充要条件是对于所有对象（包括Kharitonov多项式、顶点对象、边对象）系统都稳定，而顶点对象只是边对象的一部分，所以顶点对象稳定是判定系统鲁棒稳定的必要条件，系统鲁棒稳定则式（24）中任何一个顶点多项式必稳定，或者说式（24）中任何一个顶点多项式不稳定，系统也不可能保持鲁棒稳定。

2）巡检机器人关节电机PID控制系统鲁棒稳定充要条件的推导

Kharitonov边对象是由被控对象传递函数分子、分母的线段多项式和Kharitonov多项式组合构成的多项式的集合。分子、分母的线段多项式是指分子、分母的 4个Kharitonov多项式的线性组合而构成的4个新的多项式，其构造方式如式（25）、式（26）所示，即

则 ()Gs的Kharitonov边对象可用式（27）来描述。

所以闭环系统的Kharitonov边对象特征方程为

所以闭环系统Kharitonov边对象特征多项式为

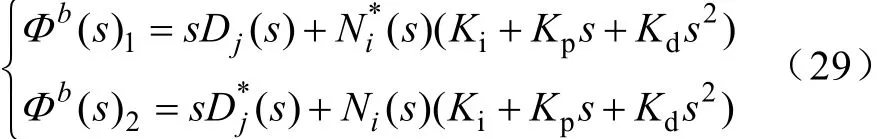
若对于 G (s)， Ni(s) = 1 (i=1 ,2,3,4)，则 Ni*(s)=Ni(s)=1，闭环系统Kharitonov边对象特征多项式可简化为式（30）、式（31）两式来描述，即

由式（30）可得系统的 4个Kharitonov边对象特征多项式，即

对于被控对象 ()Gs，将式（23）代入式（26）可得 ()Gs分母的线段多项式为

将式（33）代入式（31）可得式（34）闭环系统的另外4个Kharitonov边对象特征多项式，即

理论上的32个Kharitonov边对象特征多项式经简化后得式（32）、式（34）确定的8个多项式，其稳定性可由劳斯判据确定，它们稳定是系统鲁棒稳定的充要条件。

3 巡检机器人关节电机鲁棒PID整定方法与流程

基于上述分析，对于一个已经确定的被控对象和已知的参数摄动范围，可直接推导出关节电机控制系统PID控制器参数 pK、iK、dK的稳定域，用户在控制过程中可以动态调节这些参数，以保证关节电机在扰动情况下稳定工作。理论上讲求解稳定域直接利用劳斯判据对充要条件中的16个多项式分别列劳斯表，求取稳定性范围，再取交集就可得到稳定域，但结合文中提出的判断系统鲁棒稳定的充分条件、必要条件、充要条件，PID整定流程按以下几个步骤进行在一定程度上可进一步简化求解流程。

1）建立被控对象的传递函数数学模型并确定模型中参数的摄动范围，写出闭环系统的Kharitonov多项式、Kharitonov顶点多项式、Kharitonov边对象多项式。

2）利用常规方法整定PID控制器参数。

3）对式（15）的4个Kharitonov多项式进行稳定性判定，如果都稳定，则系统可保持鲁棒稳定（充分条件）；否则判定式（24）4个Kharitonov顶点多项式的稳定性，若式（24）中其中任何一个多项式不稳定，则系统也不可能稳定（必要条件），此时直接返回第（2）步重新整定PID参数；否则判定式（32）和式（34）两式 8个Kharitonov边对象多项式的稳定性，若8个多项式都稳定，则系统鲁棒稳定，否则返回第（2）步重新整定PID参数。判断流程如图5所示。

图5 巡检机器人鲁棒PID整定流程

4 应用举例

以机器人关节电机鲁棒PID闭环控制系统的特征多项式式（13）为算例任取一组参数及其摄动范围并来说明算法的流程。假定P的标称值为2.5，P在标称参数的20%内摄动即 P+= 3 、P-= 2 ；假定Q的标称值为3.5，Q在标称参数15%内摄动即 Q+= 4、Q-= 3 ；假定M的标称值为11.5，M在标称参数的5%内摄动即 M+= 1 2,M-= 1 0；首先利用 Z-N整定法常规PID参数 Kp= 5 .5、 Ki= 4 0、 Kd=10；为判断式（13）的稳定性，将上述参数代入式（15）得

由劳斯判据可知不满足稳定充分条件，转第二步将上述参数代入式（24）得

由劳斯判据可知不满足稳定必要条件，说明上述初始给定PID参数无法保证系统鲁棒稳定，很显然不满足充分条件和必要条件都是由于参数iK设置过大导致的，此时需重新整定获取新的PID参数，然后重复上述流程，直到系统稳定为止。上述过程可以在计算机上实现，鲁棒PID控制参数会根据巡检机器人所受扰动情况实时动态调整，以保证机械臂快速、准确、稳定的跟踪到给定值。

5 仿真实验与结果分析

利用常规PID控制器和本文鲁棒PID控制器分别对机器人关节直流电机实施控制，本文机器人关节电机选用的是Maxon无刷直流电机，其相关参数见表1。

表1 Maxon无刷直流电机参数表

由表1经计算得电机模型的标称值为P=1.15×10-5，Q=0.316，M=1.14×10-5当 P、Q、M 分别在150%、100%、60%和50%、30%、10%的范围内摄动做分别两组仿真实验，结果分别如图6、图7、图8、图9所示，其中第一组图6和图7为不同参数摄动下常规PID控制阶跃响应曲线，第二组图8和图9为不同参数摄动下鲁棒PID控制阶跃响应曲线。为了更加清楚的识别曲线之间的差别，图 7和图 9分别用Δ、*、·、+四种符号分别表示模型参数摄动 50%、30%、10%和标称模型的阶跃响应曲线。为进一步验证基于Kharitonov理论的鲁棒 PID控制效果的优越性，将其与基于H∞理论的鲁棒PID的控制效果进行对比，做第三组仿真实验，取定关节电机参数摄动为 50%和 100%，仿真结果分别如图10、图11所示。

图6 参数摄动为150%、100%、60%时常规PID控制阶跃响应曲线

图7 参数摄动为50%、30%、10%时常规PID控制阶跃响应曲线

图8 参数摄动为150%、100%、60%时鲁棒PID控制阶跃响应曲线

图9 参数摄动为50%、30%、10%时鲁棒PID控制阶跃响应曲线

图10 参数摄动为50%时H∞鲁棒PID和Khatitonov PID控制阶跃响应曲线

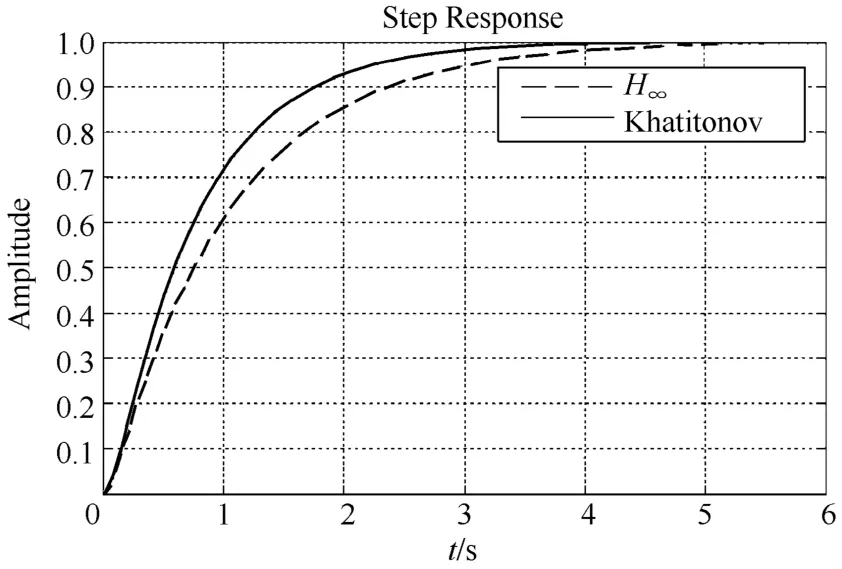
图11 参数摄动为100%时H∞鲁棒PID和Khatitonov PID控制阶跃响应曲线

由第一组仿真结果图 6、图 7可知，对于标称模型即参数无摄动的情况下采用常规PID控制可以获得较好的控制效果，如图7“+”曲线所示。随着模型参数摄动由10%～150%的逐步增大，曲线的收敛速度越来越慢，超调量增大，震荡加剧，当参数摄动在 150%时曲线已进入等幅震荡模式，无法收敛。由此可知，常规PID控制在参数不确定系统中，特别是参数摄动范围增大的情况下控制效果变得越来越差，无法保证控制系统的鲁棒性能。

由第二组仿真结果图8、图9可知，随着模型参数摄动由10%～150%的逐步增大，曲线的收敛速度会变慢，可能会有小幅震荡产生，但最终都还是可以收敛到稳定状态。当模型参数摄动由 10%～50%时，最迟约3s后可保证系统收敛；当模型参数摄动由60%～150%时，最迟约4.5s后可保证系统收敛，由此可知，鲁棒PID相对传统PID在参数不确定系统控制中具有明显优势，虽然与常规PID一样参数摄动范围增大的情况下收敛速度会有所变慢，但最终还是完全可以保证收敛，这是鲁棒PID和常规PID控制效果的本质区别。鲁棒PID能够较好地适应模型参数的不确定性对系统控制效果的影响。

由第三组仿真结果图 10、图 11可知，在不同参数摄动范围内H∞鲁棒PID和Khatitonov PID控制都能够使得系统稳定收敛，但Khatitonov PID控制效果要明显优于H∞鲁棒PID控制效果，主要表现在Khatitonov PID控制上升时间更短，收敛速度更快，Khatitonov理论相对于H∞理论更适宜于处理参数不确定系统的稳定性问题。为更清晰地比较不同参数摄动下，不同方法对机器人关节电机控制性能的影响，结合上述3组仿真结果列出不同方法机器人关节电机性能比较见表2。

表2 不同方法机器人关节电机控制性能（收敛时间）比较

此外，对比第一组和第二组仿真结果，图6和图 8为参数摄动为 60%～150%时常规 PID和鲁棒PID的控制效果，常规PID出参数摄动150%震荡外，其他几条曲线要在约 20s后才能全部收敛到稳定状态，收敛速度慢，而鲁棒PID曲线在4.5s后即可全部收敛到稳定状态。图7和图9为参数摄动为10%～50%时常规PID和鲁棒PID的控制效果，常规PID曲线要在约 12s后才能全部收敛到稳定状态，而鲁棒PID曲线在2.5s后即可全部收敛到稳定状态。由此可见鲁棒PID收敛速度大幅提高，增强了控制的实时性。综合上述分析可知基于Khatitonov理论的鲁棒 PID对于参数不确定系统具有较好的控制效果，能够满足控制系统快速、准确、稳定的设计要求，这对巡检机器人关节电机实施鲁棒PID控制为机器人的正常工作提供了强有力的保证。

6 结论

本文在建立巡检机器人关节电机PID控制系统模型的基础上，利用Kharitonov定理对该模型进行了鲁棒稳定理论分析，利用Matlab仿真实验验证了本文理论分析的正确性。值得进一步深入思考的是，本文被控对象分子为常数简化了计算量，在实际中可能会遇到理论上最多52个（充分条件4个+必要条件16个+充要条件32个）线性多项式的稳定性判断，计算量巨大，如何寻找简单易行的方法来处理这些多项式对提高算法的效率具有很大的实际意义。此外，电机参数的摄动范围如何精确标定以及如何在保证机器人稳定运行的基础上，使各关节电机协调工作能耗更少，性能更优，将是后续研究的重要内容。

[1] 张运楚, 梁自泽, 谭民. 架空输电线路巡检机器人的研究综述[J]. 机器人, 2004, 26(5)： 467-473.

[2] 张文辉, 齐乃明, 尹洪亮. 基于滑模变结构的空间机器人神经网络跟踪控制[J]. 控制理论与应用,2011(9)： 1141-1144.

[3] 高健, 黄心汉, 彭刚, 等. 移动机器人PID运动控制器参数的模糊自整定[J]. 华中科技大学学报(自然科学版), 2004, 10(S1)： 48-51.

[4] 王洪斌, 李铁龙, 郭继丽, 等. 机器人的神经网络鲁棒轨迹跟踪控制[J]. 电机与控制学报, 2005, 9(2)：145-147.

[5] 李琳, 任俊霖, 邹焱飚, 等. 基于免疫遗传算法的移动机器人轨迹跟踪[J]. 华南理工大学学报(自然科学版), 2013, 41(7)： 13-18.

[6] Tsocano R. Robust synthesis of a PID controller by uncertain multimodel information sciences, 2007,117(6)： 1441-1415.

[7] Huang Y J, Wang Y J. Robust PID tuning strategy for uncertain plants based on the Kharitonov theory[J].ISATransactions, 2000, 39： 419-431.

[8] 彭瑞, 岳继光. 基于区间分析的参数不确定系统PID鲁棒控制器设计[J]. 电机与控制学报, 2006, 10(4)：411-414.

[9] 徐峰, 李东海, 薛亚丽, 等. 基于区间多项式稳定性理论的 PID控制器[J]. 清华大学学报(自然科学版),2003, 43(12)： 1642-1645.

[10] Ho M T. Synthesis of H∞PID Controllers： AParametric Approach. Automatica, 2003, 39： 1069-1075.

[11] 吕永健, 解亮, 王海波. 基于 H∞控制的无刷直流电机鲁棒控制器[J]. 微电机, 2011, 44(1)： 55-57.

[12] 恒庆海, 鲁婧, 李丽. 无刷直流电机H∞鲁棒PI控制[J]. 中南大学学报(自然科学版), 2013, 44(S1)： 87-91.

[13] Wang Peng, Liu Feng, Mei Shengwei, et al.transmission lines inspection robot[A]. Proceedings of the 29th Chinese Control Conference July 29-31, 2010,Beijing, China, 2010.

[14] 王鹏, 刘锋, 梅生伟, 等. 高压输电线巡线机器人控制体系构建及动作控制器设计[J]. 清华大学学报(自然科学版), 2011, 51(7)： 921-927.

[15] 赵浩泉, 封锡盛, 刘开周. 基于混合灵敏度的水下机器人鲁棒控制研究[J]. 仪器仪表学报, 2007, 28(8)：606-609.

[16] Liu Kaizhou, Guo Wei, Wang Xiaohui, et al. Research on the Structure Singular Value Robust Control of Underwater Vehicle[A]. Proceedings of the 8th World Congress on Intelligent Control and Automation, July 6-9 2010, Ji’nan, China.