高中物理求最值的几种常见数学方法

赵新利

(广东省珠海市斗门区和风中学 519110)

高中物理经常涉及求最值的问题，很多都是应用数学方法来解决的，常见的方法有：利用三角函数最值的，利用均值不等式的，还有利用一元二次方程的，下面就以上三中方法附例题加以说明.

方法一利用三角函数求最值

本方法所涉及的数学知识:

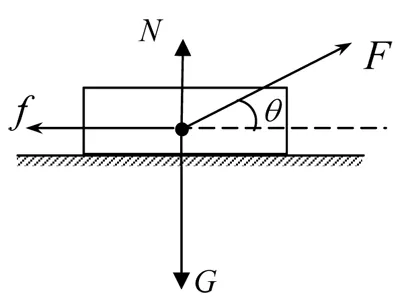
图1

例1 一质量为m的物体放在水平面上，物体与水平面的滑动摩擦因数为μ，加一大小不变的拉力F在物体上，力与水平面夹角多大时，物体的加速度a最大？(重力加速度为g)

解析假设力与水平方向成 ,物体的受力分析如图1所示：将拉力F分解到水平方向和竖直方向,

竖直方向力的关系有：

(1)Fsinθ+N=mg

水平方向力的关系有：

(2)Fcosθ-f=ma

(3)已知f=μN

联立(1)、(2)、(3)式有：

Fcosθ+μFsinθ-μmg=ma.

由数学知识有：

方法二利用均值不等式求最值

本方法所涉及的数学知识

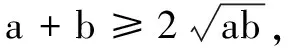
图2

例2 如图2所示,竖直放置的光滑半圆形轨道与光滑水平面AB相切于B点,半圆形轨道的最高点为C.轻弹簧一端固定在竖直挡板上,另一端有一质量为0.1 kg的小球(小球与弹簧不相连).用力将小球向左推,小球将弹簧压缩一定量时用细绳固定住.此时弹簧的弹性势能为4.05 J,烧断细绳,弹簧将小球弹出.取g=10 m/s2.

求:(1)欲使小球能通过最高点C,则半圆形轨道的半径最大为多少?

(2)欲使小球通过最高点C后落到水平面上的水平距离最大,则半圆形轨道的半径为多大?落至B点的最大距离为多少?

解析设小球离开弹簧时的速度为v1，通过最高点C的速度为v2.

(1) 从烧断细绳开始,到弹簧将小球弹离时：由机械能守恒定律有：

小球从B到C的运动过程中由机械能守恒定律有：

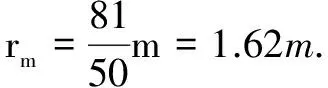
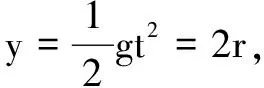
x=v3t.

由系统机械能守恒得：

由以上各式得：

由数学方法均值不等式知识知：

当8.1-4r=4r时,x有极大值

所以，当半圆形轨道的半径r为1.01 m时，小球落至B点的最大距离xmax为4.04 m.

方法三利用一元二次方程求最值

本方法所涉及的数学知识：

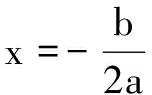
例3 一个质量为m的电子和一个静止的质量为M的原子发生正碰，碰撞的结果是：原子获得了一定的速度，并有一定的能量E储存在这个原子的内部，问电子必须具有的最小初速度是多少？

解析设电子碰撞前的速度为v0，碰撞后的速度为v1，静止的原子被碰后的速度为v2

根据动量守恒定律有：

(1)mv0=mv1+Mv2

根据能量守恒有：

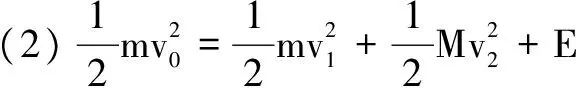
由(1)解出 ，代入(2)中可得：

化简后可得：

上面这个表达式可视为关于v1的一元二次方程，因为电子碰撞后的速度 必为实数，根据数学规律可知，应有方程的判别式Δ=b2-4ac≥0,.

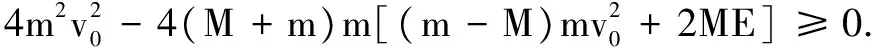
化简后可得：

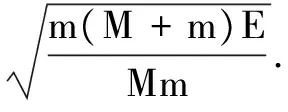
近年来，高中物理对运用数学方法解决物理问题的能力要求一直是比较高的，而在物理教学中对于大多数高中学生来说运用数学方法求解物理问题最值的能力的培养又是一大难点，其主要原因之一就是知识方法的归类总结不够到位，希望本文所介绍的几种常见求物理问题最值的方法对广大高中学生有所帮助，能够起到抛砖引玉的作用.

参考文献：

[1] 宋成福.例谈高中物理求最值问题的七种数学方法[J].湖南中学物理，2013(10).

[2] 吴静.例谈数学方法在高中物理中求极值的应用[J].中学生理科应试,2016(3).