不同土质土壤水分运移规律研究
2018-04-23王苏玉
王苏玉
(河南省信阳水文水资源勘测局,河南 信阳 464000)
1 引 言
土壤水分是植物进行光合作用、呼吸作用、养分运输等过程的重要媒介,是植物赖以生存的重要因素[1]。土壤水分的合理性直接关系到土壤中所有物质的运移过程,土壤水分运移规律与农业、水利、土壤、林业、环境、建筑等学科发展与生产实践有着密切的联系[2]。土壤水分随着土质或土壤基本特性的不同,其运动规律也不同。研究土壤水分入渗、存蓄、蒸发等运移规律问题,增加土壤水分存蓄量、减少土壤水分渗漏量及蒸发量,一直是急需进一步研究的重点[3]。近年来,我国北方地区干旱缺水严重,南方地区同样存在严重的季节性干旱,严重影响作物产量及品质[4]。了解不同土质土壤水分运移规律,增加入渗和土壤蓄水,达到减少雨季地表径流冲刷与流失,抗御旱季干旱的目的,不但能充实和完善土壤水文过程,而且对理解土壤侵蚀过程、开展过程模拟有重要的科学意义,对农田灌溉措施、水土保持措施的制定具有十分重要的实践意义。
目前针对土壤水分运移规律,已有了部分研究。王全九等[5]比较了不同土壤水分运移规律模型的精度,通过对比分析了具有明确物理意义的Philip入渗模型和Green-Ampt 入渗模型,建立了两模型参数间的内在关系,并利用一维垂直入渗实验资料对理论关系进行了比较。发现Philip入渗模型对参数精度要求较高;王春颖等[6]通过试验研究了层状夹砂土柱土壤水分运动过程,并建立了层状夹砂土柱的土壤水分入渗S-Green-Ampt 模型,指出土壤入渗率呈现先剧烈变化后平稳的规律,同时验证了该模型的科学性;范严伟等[7]基于Hydrus-1D 模型模拟了砂质夹层的土壤入渗特性,指出砂层可起到减渗的作用,当入渗阶段进入稳定入渗后,土壤水分累积入渗量呈直线趋势变化;李远等[8]基于Hydrus-1D模型模拟了土壤水盐运移规律,土壤含水率越高,将土壤湿润锋位置下移,土壤积盐区位置也随之下移。
本文通过试验手段,分别研究了不同容重下壤土和粘土的土壤水分运移规律,同时基于Philip模型模型建立了土壤水分运移模型,并基于Hydrus-1D模型模拟了不同土质土壤水分运移规律,得出的结论对了解不同土质土壤侵蚀过程有具有重要的科学意义。
2 试验方法
2.1 试验设计
试验装置由供水装置和试验土柱两部分组成,其中供水装置由带刻度供马氏瓶、供水管组成(马氏瓶是一个可以维持土柱一个定水头的供水装置),马氏瓶有机玻璃柱内径18cm(土柱直径18cm)土壤入渗曲线的测定采用马氏瓶原理取得,整个供水装置在整个实验过程都是放置在一个测量精度为0.1g的电子称上面,实验进行时电子称的示数变化代表着下渗的水量变化情况,也可以转化为下渗率的变化情况,试验土柱由带刻度有机玻璃柱和土样组成。
2.2 试验土壤选取
针对选取不同土质的壤土和粘土,充分供水情况下,野外调查不同土壤的容重平均为1.35mg/cm3,保证土壤其余条件基本一致的前途下,对不同土质土壤分别选择容重为1.25 mg/cm3、1.35 mg/cm3和1.45 mg/cm3的高度为30cm的均质土柱进行试验。
2.3 试验指标测定
2.3.1 下渗率及累积下渗率测定
下渗率的测定是根据马氏瓶的工作原理测定,具体操作流程详见文献[9]的操作步骤。由马氏瓶原理我们可以看出,在一定的时间里读出马氏瓶的刻度就是累积下渗率,而这段时间内马氏瓶水量的变化率就是这段时间里的平均下渗率。
2.3.2 Hydrus-1D模型
模型通过控制初始条件和边界条件,基于正解模块和反演模块,形成能够完整描述水流运动的数学模型,不考虑气相和温度梯度对水流运动的影响,该模型采用以含水量为因变量的一维垂直人渗问题的Richard方程[10],该模型形式如下:
(1)
其中:θ是土壤体积含水量,单位是cm3/cm3;t是时间;Z为空间坐标cm(上为正);K为非饱和主巧导水率,单位cm/d;H为压力水头单位cm;α为水流方向与垂直方向的夹角(0°代表垂向流动,90°代表水平流动);S为汇项,单位cm3/cm3/d,表示作物根系吸水,在本实验中等于零;K是非饱和导水率。
2.4 模型模拟结果评价指标体系构建
Nash-Sutcliffe系数(CD)、逐日相对均方根误差(RMSE)和Kendall一致性系数(K)可以较好地反映长时间预测序列与实测值的误差和一致性,是系统性较好的数据评价指标体系。其中,CD与K的值越大、RMSE的值越小,模型算法与实测值的一致性越好、计算精度越高,具体公式如下:
(2)
(3)
(4)
3 结果与分析
3.1 不同土质土壤下渗率及累积下渗率变化
图1为不同土质土壤不同容重下的土壤水分下渗率及累积下渗率变化趋势对比。图1显示,壤土3种不同容重下的下渗率随时间变化呈幂函数下降趋势,且土壤容重越高,同时刻土壤下渗率越低,不同容重的土壤基本在200min时,下渗率趋于稳定,容重越低,土壤水分起始下渗率越快。容重为1.25的曲线起始下渗率约为60.5mm/min,稳定下渗率大小约为14.3mm/min;容重为1.35的曲线始下渗率约为37.6mm/min,稳定下渗率约为9.7mm/min;容重为1.45的曲线始下渗率约为30.4mm/min,稳定下渗率约为5.5mm/min;粘土的土壤水分下渗率变化趋势基本相同,但相同容重下,同一时刻的土壤水分下渗率要低于壤土,3种容重下,粘土的土壤水分稳定下渗率分别为7.6 mm/min、3.7 mm/min和3.1 mm/min,均低于壤土。
由图1可以看出,不同土质不同容重下,在30min以前,曲线差异不大,随着时间推移,不同曲线差异逐渐明显,容重越小,曲线斜率越大,容重越大,曲线越平缓。最终曲线呈线性增长变化,说明该时刻土壤入渗达到了稳定下渗率阶段,直线斜率的大小与稳定下渗率基本一致。图1显示,相同容重下,不同土质的累积下渗率变化曲线不同,壤土在3种容重下的累积下渗率增长趋势分别为1.19 mm/min、0.80 mm/min和0.69mm/min,远高于粘土,表明壤土的土壤水分下渗速率高于粘土。

图1 不同土质土壤下渗率及累积下渗率变化趋势Fig.1 The trend of soil infiltration rate and cumulative infiltration rate in different soil texture
3.2 不同土质土壤下渗率Philip模型构建
土壤入渗的Philip模型将一维水分垂直运动基本方程取解的无穷级数形式,常用的Philip一维垂直入渗模型为:
I=St0.5+At
(5)
式中,I为累积入渗量,cm;S为土壤吸渗率,cm/min0.5;A为稳定入渗率,cm/min;t为时间,min。
将式(5)取时间t的导数,得到入渗率公式:
i=0.5St-0.5+A
(6)
Philip 模型具有明确的物理意义,对于短历时的入渗情况较精确。但该模型只适用于均质土壤垂直一维入渗情况,对参数精度要求较高。
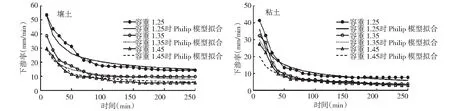
图2 不同土质土壤Philip模型计算结果拟合分析Fig.2 Fitting Analysis of Philip Model Calculation Results under different soil texture
图2为不同土质土壤Philip模型计算结果拟合对比。图2显示,Philip模型拟合的曲线与实验所测得的数据拟合效果较好,随着土壤容重越高,Philip模型曲线拟合效果越好,同时,相同容重下,粘土的拟合效果要高于壤土。
表1为不同土质土壤Philip模型计算精度对比分析。表1显示,随着容重的增加,2种土质土壤的模型方程斜率逐渐降低,表明容重越高,土壤下渗越慢,同时,相同容重下,壤土的模型方程斜率要高于粘土,这与前文的结论基本一致。同时从精度指标可以看出,容重越高,Philip模型模拟结果越好,粘土的拟合结果要高于壤土,3种容重下,粘土的模拟结果RMSE较壤土分别降低了2.72%、20.98%和5.40%,CD分别提高了10.8%、1.6%和0.7%,K值分别提高了1.31%、2.43%和5.17%,但总体来看,Philip模型在不同情况下的模拟精度均较高,CD和K值在不同情况下,与实测值的相关性均达到了极显著水平(P<0.01)。

表1 不同土质土壤Philip模型方程及精度对比Tab.1 The equation and accuracy comparison of Philip Model Calculation Results under different soil texture
3.3 Hydrus-1D模型模拟分析
选择mm为单位,设置土壤土质为1,土壤表层倾斜程度为1,模拟土壤的厚度为300;进行时间信息设置模块、输出设置、迭代步长的相应设置;上边界条件设置为定水头,下边界为自由排水,最后设置土壤剖面的图像,设置观测点,为保证研究土壤的广泛性和成果的普适性。模拟中土壤模型水力特性参数见表2。

表2 不同土质土壤水力特性参数表Tab.2 Soil hydraulic parameters different soil texture

图3 不同土质土壤Hydrus-1D模型模拟结果与实测值拟合效果对比Fig.3 The comparison between Hydrus-1D model simulation results and the measured value under different soil texture
图3为不同土质土壤Hydrus-1D模型模拟结果。图3显示,不同土质土壤在3种容重下的累积下渗率Hydrus-1D模型模拟结果与实测值拟合效果较高,基本与实测值的变化趋势相吻合,这说明Hydrus-1D模型对土壤一维水分运移模拟效果较好。同时由表3可以看出,该模型模拟对粘土的模拟效果要高于壤土,模拟结果的RMSE值仅为0.218~0.258,CD和K值均在0.85以上,且与实测值的相关性均达到了极显著水平(P<0.01),且随着土壤容重的提高,模型模拟精度逐渐提高,但整体而言,对2种土壤的模拟精度均较高,Hydrus-1D对粘土的累积下渗量的模拟好于壤土,这点与前文结论相符。
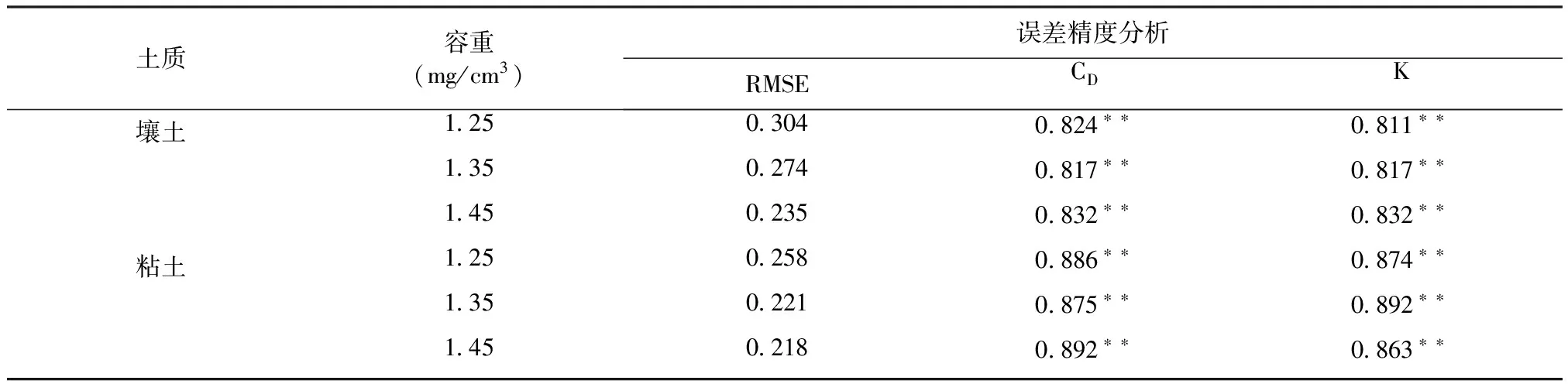
表3 Hydrus-1D模型计算结果精度Tab.3 The accuracy of Hydrus-1DModel Calculation Results
4 结 论
本文针对不同土质(壤土和粘土)在不同容重下(1.25 mg/cm3、1.35 mg/cm3和1.45 mg/cm3),通过室内试验检测土壤水分下渗率变化情况,分析不同土壤水分运移规律,基于Philip模型建立了不同情况土壤水分运移模型,并基于Hydrus-1D模型进行数值模拟分析,模拟了不同土质土壤水分累积下渗率的变化情况,得出了以下结论:
4.1 不同容重的土壤基本在200min时,下渗率趋于稳定,容重越低,土壤水分起始下渗率越快,壤土在同一时刻的土壤水分下渗率要高于粘土,且容重越高,土壤水分下渗率越高;
4.2 Philip模型模拟结果总体较好,其对粘土的模拟效果要高于壤土,模拟粘土土壤水分下渗率的RMSE较壤土低2.72%~20.98%,一致性指标CD提高了0.7%~10.8%,K值提高了1.31%~5.17%,与实测结果的相关性均达到了极显著水平(P<0.01);
4.3 Hydrus-1D模型模拟结果与实测值的变化趋势基本吻合。对粘土的模拟效果要高于壤土,模拟结果的RMSE值仅为0.218~0.258,CD和K值均在0.85以上。
参考文献:
[1] Ghannoum O. C4 photosynthesis and water stress[J]. Annals of Botany, 2009, 103(4): 635-644.
[2] 崔向慧. 干旱半干旱沙区人工植被与土壤水分环境相互作用关系研究进展[J]. 世界林业研究,2010,23(6):50-54.
[3] 李 毅,任 鑫,Horton Robert. 不同质地和夹层位置对层状土入渗规律的影响[J]. 排灌机械工程学报,2012,30(4):486-490.
[4] 周巧兰,刘晓燕.我国南方干旱成因与对策[J]. 上海师范大学学报(自然科学版),2005,34(3):84-90.
[5] 王全九,来剑斌,李 毅. Green-Ampt模型与Philip入渗模型的对比分析[J]. 农业工程学报,2013,18(2):13-16.
[6] 王春颖,毛晓敏,赵 兵. 层状夹砂土柱室内积水入渗试验及模拟[J]. 农业工程学报,2010,26(11):61-67.
[7] 范严伟,黄 宁,马孝义,等. 应用HYDRUS-1D模拟砂质夹层土壤入渗特性[J]. 土壤,2016,48(1):193-200.
[8] 李 远,郑旭荣,王振华,等. 基于Hydrus-1D 的土壤水盐运移数值模拟[J]. 中国农学通报,2014,30(35):172-177.
[9] 张建丰. 黄土区层状土入渗特性及其指流的实验研究[D]. 咸阳:西北农林科技大学,2004.
[10] 何康康,杨艳敏,杨永辉. 基于HYDRUS-1D 模型的华北低平原区不同微咸水利用模式下土壤水盐运移的模拟[J]. 中国生态农业学报,2016,24(8):1059-1070.
